В какой системе счисления хранятся и обрабатываются числа в памяти компьютера

Обновлено: 15.01.2025

Тебе известно, что компьютер работает только с двоичным кодом. \(0\) и \(1\) обозначают два устойчивых состояния: вкл/выкл, есть ток/нет тока и т. д. Оперативная память представляет собой контейнер, который состоит из ячеек. В каждой ячейке хранится одно из возможных состояний: \(0\) или \(1\). Одна ячейка — \(1\) бит информации или представляет собой разряд некоторого числа.

Целые числа в памяти компьютера хранятся в формате с фиксированной запятой . Такие числа могут храниться в \(8\), \(16\), \(32\), \(64\)-разрядном формате.

Для целых неотрицательных чисел в памяти компьютера выделяется \(8\) ячеек (бит) памяти.

Минимальное число для такого формата: \(00000000\). Максимальное: \(11111111\).

Переведём двоичный код в десятичную систему счисления и узнаем самое большое число, которое можно сохранить в восьмибитном формате.

1 × 2 7 + 1 × 2 6 + 1 × 2 5 + 1 × 2 4 + 1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 1 × 2 0 = 255 10 .

Если целое неотрицательное число больше \(255\), то оно будет храниться в \(16\)-разрядном формате и занимать \(2\) байта памяти, то есть \(16\) бит.

Подумай! Какое самое большое число можно записать в \(16\)-разрядном формате?

Чем больше ячеек памяти отводится под хранение числа, тем больше диапазон значений.

В таблице указаны диапазоны значений для \(8\), \(16\) и \(32\)-разрядных форматов.

Для \(n\)-разрядного представления диапазон чисел можно вычислить следующим образом: от \(0\) до 2 n − 1 .

Запишем целое беззнаковое число \(65\) в восьмиразрядном представлении. Достаточно перевести это число в двоичный код.

Это же число можно записать и в \(16\)-разрядном формате.

Для целых чисел со знаком в памяти отводится \(2\) байта информации (\(16\) бит). Старший разряд отводится под знак: \(0\) — положительное число; \(1\) — отрицательное число. Такое представление числа называется прямым кодом.

Для хранения отрицательных чисел используют дополнительный и обратный коды, которые упрощают работу процессора. Но об этом ты узнаешь в старших классах.

После того, как мы узнали об основных единицах для измерения информации необходимо разобраться с тем, как в ЭВМ хранятся различные типы данных. В этой статье мы поговорим про представление чисел в компьютере.

Основные понятия и положения

Прежде чем начать разбираться в теме, следует понимать, что все ЭВМ, на данный момент времени, работают с двоичной системой счисления. Это значит, что и вся информация (звуковая, графическая или текстовая) хранится в памяти ПК в виде последовательностей нулей и единиц.

Схематично компьютерная память выглядит так, как показано на схеме ниже:

Как видно из рисунка внутренняя память представляет собой разряды, каждый из которых содержит один бит информации (0 или 1). А восемь битовых кластеров образуют один байт (машинное слово).

Машинное слово – минимально адресуемая ячейка памяти, которую за раз можно обработать командой процессора. То есть минимально процессор может обработать один байт.

Отсюда также вытекает правило, что данные в компьютере представляются дискретно (отдельно). В качестве примера приведем изображение на мониторе. Оно состоит из точек (пикселей). Цвет же каждой точки задается последовательностью из 0 и 1.

Это интересно Представление информации в компьютере. Единицы измерения информации

Представление чисел в компьютере

Существует несколько вариантов для отображения чисел в ЭВМ, и зависят они от формата числа.

Представление целых чисел в ЭВМ

Для представления целых чисел, в вычислительных машинах существует несколько способов, которые используют 8,16, 24 или 32 разряда памяти (1, 2, 3 и 4 байта).

Первым способом является беззнаковое представление. С его помощью представляются только целые положительные величины, которые не участвуют в арифметических операциях и выступают в роли констант (дата, время и т.д.).

Чтобы представить число в беззнаковой форме необходимо перевести его в двоичную систему счисления и дополнить с начала нулями до нужной разрядности (дополняем до 1,2,3 или 4 байт).

Также следует отметить, что есть ограничения на количество чисел, которые можно представить в n разрядной ячейке. Для беззнаковых величин оно составляет \( 2^n \).

Пример: Перевести 54 в беззнаковый формат.

Находим представление 54 в бинарной системе счисления:

Итого \( 54_ \) равняется \( 110110_ \).

Дополняем результат до одной из стандартных разрядностей (8 бит) = 00110110.

Ответ: 00110110.

Для представления чисел, которые участвуют в вычислительных операциях, используется представление со знаком. В такой форме записи старший разряд всегда отводится под знак (0 для положительных чисел и 1 для отрицательных).

В случае со знаковым представлением также существуют ограничения. Так как один разряд отводится под знак, то в n-разрядную ячейку можно записать \( (2^ -1) \) положительных и \( 2^ \) отрицательных значений.

Для того чтобы перевести число в обратный и дополнительный код вам надо:

Взять его значение по модулю и перевести в двоичную систему счисления (получим прямой код).
Все нули заменить на 1, а единицы на нули (получаем обратный код).
Для получения дополнительного кода прибавляем к нулевому разряду единицу.

Пример: Перевести -54 в дополнительный код.

Почему же для хранения отрицательных чисел используют обратный или дополнительный код? Это позволяет изменить операцию вычитания на операцию сложения. В противном случае компьютеру бы каждый раз приходилось выяснять, где положительная величина, а где отрицательная и после этого сравнивать их модули, для определения конечного знака, что очень сильно усложняло бы весь алгоритм.

Представление вещественных чисел

Всего существует два способа для представления множества вещественных значений – естественная или экспоненциальная форма.

В жизни мы пользуемся естественной формой. Так число 42,6 мы можем записать несколькими способами. Например:

\( 426*10^ \) ;
\( 4,26*10^1 \) ;
\( 42,6*10^0 \) .

В компьютере же используется экспоненциальная форма записи. Выглядит она так:

Здесь m – мантисса, которая представляет собой правильную дробь (в правильных дробях числитель меньше знаменателя).

q – система счисления, в которой представлено число.

P – порядок.

Чем больше бит отводится под мантиссу, тем точнее представляемая величина, чем больше ячеек отводится под порядок, тем шире диапазон от наименьшего числа, до наибольшего числа, представляемого в компьютере при заданном формате.

Так как компьютерная память величина дискретная и конечная, то и множество вещественных чисел, с которым работает ЭВМ также конечно.

Видео

Заключение

Вот мы и разобрались с представлением чисел в компьютере и информатике. Краткий материал из данной статьи вы можете использовать для своей онлайн-презентации. При возникновении вопросов оставляйте их в комментариях.

Числовые данные обрабатываются в компьютере в двоичной системе счисления. Числа хранятся в памяти компьютера в двоичном коде, т. е. в виде последовательности нулей и единиц, и могут быть представлены в формате с фиксированной или плавающей запятой.

Целые числа хранятся в памяти в формате с фиксированной запятой. При таком формате представления чисел для хранения целых неотрицательных чисел отводится регистр памяти, состоящий из восьми ячеек памяти (8 бит). Каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда и вне разрядной сетки. Например, число 11001101₂ будет храниться в регистре памяти следующим образом:

Максимальное значение целого неотрицательного числа, которое может храниться в регистре в формате с фиксированной запятой, можно определить из формулы: 2 n – 1, где п – число разрядов числа. Максимальное число при этом будет равно 2 8 – 1 = 255₁₀ = 11111111₂и минимальное 0₁₀ = 00000000₂. Таким образом, диапазон изменения целых неотрицательных чисел будет находиться в пределах от 0 до 255₁₀.

В отличие от десятичной системы в двоичной системе счисления при компьютерном представлении двоичного числа отсутствуют символы, обозначающие знак числа: положительный (+) или отрицательный (-), поэтому для представления целых чисел со знаком в двоичной системе используются два формата представления числа: формат значения числа со знаком и формат дополнительного кода. В первом случае для хранения целых чисел со знаком отводится два регистра памяти (16 бит), причем старший разряд (крайний слева) используется под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное, то – 1. Например, число 536₁₀ = 0000001000011000₂ будет представлено в регистрах памяти в следующем виде:

а отрицательное число -536₁₀ = 1000001000011000₂ в виде:

Максимальное положительное число или минимальное отрицательное в формате значения числа со знаком (с учетом представления одного разряда под знак) равно 2 n-1 – 1 = 2 16- 1 – 1 = 2 15 – 1 = 32767₁₀ = 111111111111111₂ и диапазон чисел будет находиться в пределах от -32767₁₀ до 32767.

Наиболее часто для представления целых чисел со знаком в двоичной системе применяется формат дополнительного кода, который позволяет заменить арифметическую операцию вычитания в компьютере операцией сложения, что существенно упрощает структуру микропроцессора и увеличивает его быстродействие.

Для представления целых отрицательных чисел в таком формате используется дополнительный код, который представляет собой дополнение модуля отрицательного числа до нуля. Перевод целого отрицательного числа в дополнительный код осуществляется с помощью следующих операций:

1) модуль числа записать прямым кодом в п (п = 16) двоичных разрядах;

2) получить обратный код числа (инвертировать все разряды числа, т. е. все единицы заменить на нули, а нули – на единицы);

3) к полученному обратному коду прибавить единицу к младшему разряду.

Например, для числа -536₁₀ в таком формате модуль будет равен 0000001000011000₂, обратный код – 1111110111100111, а дополнительный код – 1111110111101000. Проверим полученное значение дополнительного кода с помощью калькулятора. Для этого введем значение модуля числа -536₁₀, т. е. число 536₁₀, и с помощью опционной кнопки Bin преобразуем это число, представленное в десятичной системе счисления, в двоичную систему, предварительно установив опционную кнопку 2 байта. Нажав кнопку Not калькулятора, получим обратный код числа, а прибавив к обратному коду двоичную единицу, – дополнительный код. Окончательный результат получим в поле окна программы Калькулятор (рис. 2.6). Можно поступить еще проще: набрав на калькуляторе число -536₁₀ и активизировав кнопку Bin, получить дополнительной код этого числа в двоичной системе счисления.

Рис. 2.6. Результат получения дополнительного кода

Необходимо помнить, что дополнительный код положительного числа – само число.

Для хранения целых чисел со знаком помимо 16-разрядного компьютерного представления, когда используются два регистра памяти (такой формат числа называется также форматом коротких целых чисел со знаком), применяются форматы средних и длинных целых чисел со знаком. Для представления чисел в формате средних чисел используется четыре регистра (4 х 8 = 32 бит), а для представления чисел в формате длинных чисел – восемь регистров (8 х 8 = 64 бита). Диапазоны значений для формата средних и длинных чисел будут соответственно равны: -(2 31 – 1) … + 2 31 – 1 и -(2 63 -1) … + 2 63 – 1.

Компьютерное представление чисел в формате с фиксированной запятой имеет свои преимущества и недостатки. К преимуществам относятся простота представления чисел и алгоритмов реализации арифметических операций, к недостаткам – конечный диапазон представления чисел, который может быть недостаточным для решения многих задач практического характера (математических, экономических, физических и т. д.).

Вещественные числа (конечные и бесконечные десятичные дроби) обрабатываются и хранятся в компьютере в формате с плавающей запятой. При таком формате представления числа положение запятой в записи может изменяться. Любое вещественное число Къ формате с плавающей запятой может быть представлено в виде:

где А – мантисса числа; h – основание системы счисления; р – порядок числа.

Выражение (2.7) для десятичной системы счисления примет вид:

Такая форма представления числа также называется нормальной. С изменением порядка запятая в числе смещается, т. е. как бы плавает влево или вправо. Поэтому нормальную форму представления чисел называют формой с плавающей запятой. Десятичное число 15,5, например, в формате с плавающей запятой может быть представлено в виде: 0,155 · 10 2 ; 1,55 · 10 1 ; 15,5 · 10 0 ; 155,0 · 10 -1 ; 1550,0 · 10 -2 и т. д. Эта форма записи десятичного числа 15,5 с плавающей запятой не используется при написании компьютерных программ и вводе их в компьютер (устройства ввода компьютеров воспринимают только линейную запись данных). Исходя из этого выражение (2.7) для представления десятичных чисел и ввода их в компьютер преобразовывают к виду

где Р – порядок числа,

т. е. вместо основания системы счисления 10 пишут букву Е, вместо запятой – точку, и знак умножения не ставится. Таким образом, число 15,5 в формате с плавающей запятой и линейной записи (компьютерное представление) будет записано в виде: 0.155Е2; 1.55Е1; 15.5Е0; 155.0Е-1; 1550.0Е-2 и т.д.

Независимо от системы счисления любое число в форме с плавающей запятой может быть представлено бесконечным множеством чисел. Такая форма записи называется ненормализованной. Для однозначного представления чисел с плавающей запятой используют нормализованную форму записи числа, при которой мантисса числа должна отвечать условию

где |А| — абсолютное значение мантиссы числа.

Условие (2.9) означает, что мантисса должна быть правильной дробью и иметь после запятой цифру, отличную от нуля, или, другими словами, если после запятой в мантиссе стоит не нуль, то число называется нормализованным. Так, число 15,5 в нормализованном виде (нормализованная мантисса) в форме с плавающей запятой будет выглядеть следующим образом: 0,155 · 10 2 , т. е. нормализованная мантисса будет A = 0,155 и порядок Р = 2, или в компьютерном представлении числа 0.155Е2.

Числа в форме с плавающей запятой имеют фиксированный формат и занимают в памяти компьютера четыре (32 бит) или восемь байт (64 бит). Если число занимает в памяти компьютера 32 разряда, то это число обычной точности, если 64 разряда, то это число двойной точности. При записи числа с плавающей запятой выделяются разряды для хранения знака мантиссы, знака порядка, мантиссы и порядка. Количество разрядов, которое отводится под порядок числа, определяет диапазон изменения чисел, а количество разрядов, отведенных для хранения мантиссы, – точность, с которой задается число.

При выполнении арифметических операций (сложение и вычитание) над числами, представленными в формате с плавающей запятой, реализуется следующий порядок действий (алгоритм) :

1) производится выравнивание порядков чисел, над которыми совершаются арифметические операции (порядок меньшего по модулю числа увеличивается до величины порядка большего по модулю числа, мантисса при этом уменьшается в такое же количество раз);

2) выполняются арифметические операции над мантиссами чисел;

3) производится нормализация полученного результата.

Поясним сказанное выше на примерах.

Пример 1

Произведем сложение двух чисел 0,5 · 10 2 и 0,8 · 10 3 в формате с плавающей запятой.

Проведем выравнивание порядков и сложение мантисс 0,05 · 10 3 + 0,8 · 10 3 = 0,85 · 10 3 . Полученная мантисса 0,85 является нормализованной, так как удовлетворяет условию (2.9).

Пример 2

Произведем сложение двух чисел 0,1 · 2 2 и 0,1 · 2 3 в формате с плавающей запятой.

Проведем выравнивание порядков и сложение мантисс: 0,01 · 2 3 + 0,1 · 2 3 = 0,11 · 2 3 . Полученная мантисса 0,11 является нормализованной, так как удовлетворяет условию (2.9).

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

5.1. Поиск на локальном компьютере

5.1. Поиск на локальном компьютере Самой простой задачей поиска является поиск на локальном компьютере. В этом случае множество проблем решается автоматически, и вам остается разобраться с несколькими оставшимися: где и как искать.Если вы точно или хотя бы приблизительно

Получение сведений о компьютере

Получение сведений о компьютере С помощью базы данных CIMOM можно также определить конфигурацию операционной системы. Метод определения конфигурации подобен методу определения установленных на компьютере компонентов, поэтому будет рассмотрена лишь часть кода, с помощью

3. Представление чисел в ЭВМ

3. Представление чисел в ЭВМ 32-разрядные процессоры могут работать с оперативной памятью емкостью до 232-1, а адреса могут записываться в диапазоне 00000000 – FFFFFFFF. Однако в реальном режиме процессор работает с памятью до 220-1, а адреса попадают в диапазон 00000 – FFFFF. Байты памяти

3.1.1. Аппаратное представление целых чисел

3.1.1. Аппаратное представление целых чисел Delphi относится к языкам, в которых целые типы данных максимально приближены к аппаратной реализации целых чисел процессором. Это позволяет выполнять операции с целочисленными данными максимально быстро, но заставляет

5.1. Представление чисел в языке Ruby

11.20. Представление больших чисел фиксированного размера

11.20. Представление больших чисел фиксированного размера ПроблемаТребуется выполнить операции с числами, размер которых превышает размер типа long int.РешениеШаблон BigInt в примере 11.38 использует bitset из заголовочного файла <bitset> для того, чтобы можно было представить целые

Преобразования чисел

Преобразования чисел В случае встроенных числовых типов (sbyte, int, float и т.д.) явное преобразование требуется тогда, когда вы пытаетесь сохранить большее значение в меньшем контейнере, поскольку при этом может происходить потеря данных. По сути, это способ сказать

СОРТИРОВКА ЧИСЕЛ

СОРТИРОВКА ЧИСЕЛ Одним из наиболее распространенных тестов для машин является сортировка. Мы хотим разработать программу для сортировки целых чисел. Снова применим принцип черного ящика и подумаем в терминах ввода и вывода. Наш общий замысел, показанный на рис. 10.4,

Воспроизведение звука на компьютере

Воспроизведение звука на компьютере Воспроизведение цифрового звука – процесс, обратный оцифровке. Устройство, входящее в состав звуковой карты компьютера, – цифроаналоговый преобразователь (ЦАП) получает от программы-проигрывателя последовательность записей

Форматирование чисел

Форматирование чисел Мы уже познакомились с функцией языка XPath string, которая конвертирует свой аргумент в строку. Эта функция может преобразовать в строку и численное значение, но возможности ее при этом сильно ограничены.К счастью, XSLT предоставляет мощные возможности

1.1. Немного о компьютере

1.1. Немного о компьютере Во все времена человек пытался облегчить себе выполнение тех или иных работ, в результате чего появлялись различные приспособления. Однако процессы становились все сложнее, и существующие механизмы уже не справлялись со своими задачами и не

Настройка соединения на компьютере

Настройка соединения на компьютере Настройка компьютера заключается в установке и настройке модема и настройке удаленного соединения. В нашем случае установка модема означает только установку его драйвера. Драйвер может быть найден и установлен на ваш компьютер

Телевизор в компьютере

Телевизор в компьютере Тем пользователям, которые привыкли к постоянно работающему телевизору, полезной покажется возможность современного компьютера показывать телепрограммы на экране монитора.Действительно, можно настроить систему так, чтобы телепрограмма шла,

2. Представление чисел в ЭВМ. Формализованное понятие алгоритма

2. Представление чисел в ЭВМ. Формализованное понятие алгоритма 32-разрядные процессоры могут работать с оперативной памятью емкостью до 232-1, а адреса могут записываться в диапазоне 00000000 – FFFFFFFF. Однако в реальном режиме процессор работает с памятью до 220-1, а адреса

Исправляем ошибки на компьютере

Исправляем ошибки на компьютере Кадрирование Внимательно посмотрите на фотографию, представьте, что это не ваша работа, а снимок другого человека. Определите, без чего фото будет как минимум не хуже при сохранении сюжета, и смело кадрируйте — обрезайте и удаляйте все

Тренировать внимание на компьютере?

Тренировать внимание на компьютере? «Допустим, это верно в отношении телевидения. Но ведь есть исследования, которые показывают, что внимание можно даже тренировать на компьютере!» — возразят мне в этом месте те, кто охотно сидит перед компьютером и расстреливает

Оперативная память компьютера состоит из ячеек, каждая из которых представляет собой физическую систему, состоящую из некоторого числа однородных элементов. Эти элементы обладают двумя устойчивыми состояниями, одно из которых соответствует нулю, а другое — единице. Каждый такой элемент служит для хранения одного из битов — разряда двоичного числа. Именно поэтому каждый элемент ячейки называют битом или разрядом (рис. 1.2).

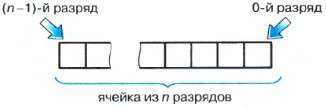
Рис. 1.2. Ячейка памяти

Для компьютерного представления целых чисел используется несколько различных способов, отличающихся друг от друга количеством разрядов (под целые числа обычно отводится 8, 16, 32 или 64 разряда) и наличием или отсутствием знакового разряда. Беззнаковое представление можно использовать только для неотрицательных целых чисел, отрицательные числа представляются только в знаковом виде.

Беззнаковое представление используется для таких объектов, как адреса ячеек, всевозможные счётчики (например, число символов в тексте), а также числа, обозначающие дату и время, размеры графических изображений в пикселях и т. д.

Максимальное значение целого неотрицательного числа достигается в случае, когда во всех разрядах ячейки хранятся единицы. Для n-разрядного представления оно будет равно 2 n -1. Минимальное число соответствует п нулям, хранящимся в n разрядах памяти, и равно нулю.

Ниже приведены максимальные значения для беззнаковых целых n-разрядных чисел:

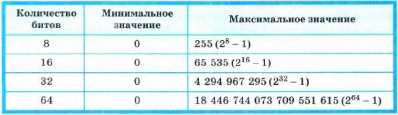
Для получения компьютерного представления беззнакового целого числа достаточно перевести число в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.

Пример 1. Число 53₁₀ = 110101₂ в восьмиразрядном представлении имеет вид:

Это же число 53 в шестнадцати разрядах будет записано следующим образом:

При представлении со знаком самый старший (левый) разряд отводится под знак числа, остальные разряды — под само число. Если число положительное, то в знаковый разряд помещается 0, если число отрицательное — 1. Такое представление чисел называется прямым кодом.

В компьютере прямые коды используются для хранения положительных чисел в запоминающих устройствах, для выполнения операций с положительными числами.

Презентация «Представление информации в компьютере» (Open Document Format)

Ссылки на ресурсы ЕК ЦОР

Федеральный центр информационных образовательных ресурсов:

Представление вещественных чисел

Любое вещественное число А может быть записано в экспоненциальной форме:

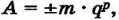
где:

m — мантисса числа;
q — основание системы счисления;
p — порядок числа.

Например, число 472 ООО ООО может быть представлено так: 4,72 • 10 8 , 47,2 • 10 7 , 472,0 • 10 6 и т. д.

С экспоненциальной формой записи чисел вы могли встречаться при выполнении вычислений с помощью калькулятора, когда в качестве ответа получали записи следующего вида: 4.72Е+8.

Здесь знак «Е» обозначает основание десятичной системы счисления и читается как «умножить на десять в степени».

Из приведённого выше примера видно, что положение запятой в записи числа может изменяться.

Для единообразия мантиссу обычно записывают как правильную дробь, имеющую после запятой цифру, отличную от нуля. В этом случае число 472 ООО ООО будет представлено как 0,472 • 10 9 .

Вещественное число может занимать в памяти компьютера 32 или 64 разряда. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.

Пример:

Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка числа, а точность определяется количеством разрядов, отведённых для хранения мантиссы.

Максимальное значение порядка числа для приведённого выше примера составляет 1111111₂ = 127₁₀, и, следовательно, максимальное значение числа:

0,11111111111111111111111 • 10 1111111

Попытайтесь самостоятельно выяснить, каков десятичный эквивалент этой величины.

Широкий диапазон представления вещественных чисел важен для решения научных и инженерных задач. Вместе с тем следует понимать, что алгоритмы обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел.

САМОЕ ГЛАВНОЕ

Для компьютерного представления целых чисел используются несколько различных способов, отличающихся друг от друга количеством разрядов (8, 16, 32 или 64) и наличием или отсутствием знакового разряда.

Для представления беззнакового целого числа его следует перевести в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.

При представлении со знаком самый старший разряд отводится под знак числа, остальные разряды — под само число. Бели число положительное, то в знаковый разряд помещается 0, если число отрицательное, то 1. Положительные числа хранятся в компьютере в прямом коде, отрицательные — в дополнительном.

При хранении в компьютере вещественных чисел выделяются разряды на хранение знака порядка числа, самого порядка, знака мантиссы и мантиссы. При этом любое число записывается так:

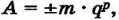
где:

m — мантисса числа;
q — основание системы счисления;
p — порядок числа.

Вопросы и задания

2. Как в памяти компьютера представляются целые положительные и отрицательные числа?

3. Любое целое число можно рассматривать как вещественное, но с нулевой дробной частью. Обоснуйте целесообразность наличия особых способов компьютерного представления целых чисел.

а) 01001100;
б) 00010101.

7. Запишите следующие числа в естественной форме:

а) 0,3800456 • 10 2 ;
б) 0,245 • 10 -3 ;
в) 1,256900Е+5;
г) 9,569120Е-3.

8. Запишите число 2010,0102₁₀ пятью различными способами в экспоненциальной форме.

9. Запишите следующие числа в экспоненциальной форме с нормализованной мантиссой — правильной дробью, имеющей после запятой цифру, отличную от нуля:

10. Изобразите схему, связывающую основные понятия, рассмотренные в данном параграфе.

Электронное приложение к уроку

Презентация «Представление информации в компьютере» (Open Document Format)

Ссылки на ресурсы ЕК ЦОР

Федеральный центр информационных образовательных ресурсов:

Презентации, плакаты, текстовые файлы

Вернуться к материалам урока

Ресурсы ЭОР

Cкачать материалы урока

Формы организации учащихся на уроке: индивидуальная, фронтальная

Используемое оборудование: компьютеры, интерактивная доска

Программное обеспечение: презентация к уроку, проверочный тест.

I. Организационный момент

Приветствие, проверка письменного домашнего задания.

II. Актуализация полученных знаний

Учащиеся (несколько человек) проходят тест на компьютерах по теме: «Системы счисления». (Приложение 1)

Для остальных учащихся фронтальный опрос.

Вопросы для фронтального опроса:

III. Изучение нового материала (Презентация)

форма с фиксированной точкой (применяется к целым числам)
форма с плавающей точкой (применяется к вещественным числам)

Представление целых чисел в форме с фиксированной запятой

Часть памяти компьютера, в которой хранится одно число – ячейка. Минимальный размер ячейки, где может храниться целое число – 8 бит или 1 байт.
Представим число 42₁₀ в двоичной системе счисления, а затем представим как будет выглядеть это число в памяти компьютера.
42₁₀ = 101010₂.

Запишем полученное число в восьмиразрядную ячейку. Запись в ячейку производится с конца, то есть последняя цифра числа записывается в последний разряд ячейки, потом предпоследнюю цифру в предпоследний разряд ячейки и так далее пока не закончится число. Свободные разряды слева заполняются нулями.

Самый старший разряд (первый слева) – хранит знак числа. Если число положительное, то этот разряд равен 0, если отрицательное – 1.

Таким образом, самое большее положительное число, которое можно вписать в восьмиразрядную сетку имеет вид:

И это число 1111111₂ = 127₁₀
Максимальное целое положительное число, помещающееся в восьмиразрядную ячейку, равно 127.

Рассмотрим представление в памяти компьютера целых отрицательных чисел

Записать внутреннее представление соответствующего ему положительного числа
Записать обратный код полученного числа заменой во всех разрядах 0 на 1, и 1 на 0.
К полученному числу прибавить 1.

Представим внутреннее представление числа – 42₁₀ в восьмиразрядной ячейке: 42₁₀ = 101010₂

1) 00101010
2) 11010101 это обратный код
3) + 1
11010110 получили представление числа – 42₁₀ в восьмиразрядной ячейке.

Старший разряд получил значение 1 автоматически. Единица в старшем разряде – признак отрицательного числа.
Сложим числа 42 и – 42. Должны получить 0, проверим:

+ 00101010
11010110
100000000 получили число, старший разряд которого выходит за пределы восьмиразрядной ячейки, таким образом восьмиразрядная ячейка заполнена нулями, т.е. полученное при сложение число равно 0.

Представление восьмиразрядного отрицательного числа – Х дополняет представление соответствующего положительного числа Х до значения 2 8 . Поэтому представление отрицательного целого числа называется дополнительным кодом.

Диапазон представления целых чисел в восьмиразрядной ячейке:

В 16-рядной ячейке можно получить числа диапазоном:

В 32-разрядной ячейке можно получить числа диапазоном:

Общая формула для диапазона целых чисел в зависимости от разрядности N ячейки:

Представление целых чисел в форме с плавающей запятой.

Вещественные числа это тоже, что и действительные числа. Из курса математике вам известно, что к действительным числам относятся целые и дробные числа.
Всякое вещественное число X записывается в виде произведения мантиссы m и основания системы счисления p в некоторой целой степени n, которую называют порядком:

Например, число 25,324 = 0,25324 · 10 2
мантисса m = 0,25324, n = 2 – порядок. Порядок указывает, на какое количество позиций и в каком направлении должна сместится десятичная запятая в мантиссе.
Чаще всего для хранения вещественных чисел в памяти компьютера используется 32-разрядная или 64-разрядная ячейка. В первом случае это будет с обычной точностью, во-втором случае с удвоенной точностью. В ячейке хранятся два числа в двоичной системе счисления: мантисса и порядка.
Диапазон вещественных чисел ограничен, но он значительно шире, чем при представление целых чисел в форме с фиксированной запятой.
Например, при использовании 32-разрядной ячейки этот диапазон следующий:

Результаты машинных вычислений с вещественными числами содержат погрешность. При удвоенной точности погрешность уменьшается. Выход из диапазона (переполнение) приводит к прерыванию работы процессора.

IV. Закрепление изученного материала

Выполнить самостоятельно задания №3(а,б) и №4(а,б) на странице учебника 105 с последующей проверкой

а) Записать внутреннее представление числа 32 в восьмиразрядную ячейку 32₁₀ = 100000₂

Значит внутреннее представление числа 32 в восьмиразрядную ячейку: 00100000

б) Записать внутреннее представление числа –32 в восьмиразрядную ячейку
32 имеет представление 00100000
Обратный код 11011111
+1
11100000
Значит внутреннее представление числа –32 в восьмиразрядную ячейку: 11100000

а) Определить какому десятичному числу соответствует двоичный код 00010101 восьмиразрядного представления целого числа.

Видим, что первый разряд – 0, значит число положительное.

Переведём число 10101₂ в десятичную систему счисления:

1 · 2 4 + 0 · 2 3 + 1 · 2 2 + 0 · 2 1 + 1 · 2 0 = 16 + 4 + 1 = 21₁₀

Значит двоичный код 00010101 восьмиразрядного представления целого числа 21₁₀.

б) Определить какому десятичному числу соответствует двоичный код 11111110 восьмиразрядного представления целого числа.

Видим, что первый разряд – 1, значит число отрицательное. Для нахождения десятичного числа выполним алгоритм дополнительного кода в обратном порядке, а именно:

1) Вычтем из данного числа 1

2) Заменим 1 на 0 и 0 на 1

3) Переведём двоичное число 10₂ в десятичную систему счисления.

Таким образом, двоичный код 11111110 восьмиразрядного представления целого числа 2₁₀.

Задание: представить вещественное число

в нормализованной форме с плавающей точкой в десятичной системе счисления.

а) 0,0050589 = 0,50589 · 10 –2
б) 1234,0456 = 0,12340456 · 10 4

V. Итог урока

– Сегодня на уроке вы узнали, каким образом хранятся числа в памяти компьютера. Как зависит диапазон значений чисел от размера ячейки, в которой хранится число.
Выставление оценок за урок (тест и задания №3, №4)

Читайте также: