Как сделать уравнение в паскале
1. Энциклопедический словарь юного математика [Текст] / Сост. А.П. Савин, гл. ред. Б.В. Гнеденко, ред. В.Д. Белоусов и др. – 2-е изд., перераб. и доп. – М.: Педагогика, 1989. – 352с.
2. Смышляев В.К. Все о великих математиках [Текст] / В.К. Смышляев. – 2-е изд., перераб. и доп. – М.: Марийское книжное издательство, 1977. – 224 с.
Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, иррациональных уравнений, неравенств и их систем.
Одна из основных целей изучения школьного курса математики заключается в овладении способами решения алгебраических уравнений второй степени и приводимых к ним уравнений. В школьном курсе изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения.
Практически все, что окружает современного человека – это все так или иначе связано с математикой. Последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в дальнейшем данная тенденция сохранится. Решение многих практических задач сводится к решению различных видов уравнений. При этом актуальным является использование ЭВМ и специального ПО при решении уравнений.
Цель работы: Разработка программы нахождения корней уравнения второй степени в среде программирования Паскаль-ABC.
1) Ознакомиться с историей квадратных уравнений и методами их решения.
2) Освоить приемы программирования в интегрированной среде Паскаль-ABC.
3) Разработать алгоритм и блок-схему нахождения корней квадратных уравнений.
4) Создать программу нахождения корней и протестировать её.
Объект исследования: уравнения второй степени.
Предмет исследования: Паскаль-программа решения уравнений второй степени в среде Паскаль-ABC.
История квадратных уравнений и методы их решений
Необходимость решать уравнения не только первой степени, но и второй ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков, с развитием астрономии, военного дела и нуждами самой математики. Первые упоминания о способах решения уравнений, которые мы сейчас называем квадратными, относятся ко второму тысячелетию до н.э. Это эпоха расцвета Вавилона и Древнего Египта.
Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и полные квадратные уравнения. Правила решения этих уравнений, изложенные в вавилонских источниках, совпадает по существу с современными, но в этих текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
В XVI веке французский юрист, тайный советник короля Франции и математик Франсуа Виет (1540-1603) впервые вводит в обращение буквенные обозначения не только для неизвестных величин, но и для данных, то есть коэффициентов уравнения. Франсуа Виет – замечательный французский математик, положивший начало алгебре как науке о преобразовании выражений, о решении уравнений в общем виде, создатель буквенного исчисления. Виет первым стал обозначать буквами не только неизвестные, но и данные величины. Тем самым ему удалось внедрить в науку великую мысль о возможности выполнять алгебраические преобразования над символами, т.е. ввести понятие математической формулы. Этим он внес решающий вклад в создание буквенной алгебры, чем завершил развитие математики эпохи Возрождения и подготовил почву для появления результатов Ферма, Декарта, Ньютона.
Общее правило решения квадратных уравнений, было сформулировано немецким математиком М. Штифелем (1487-1567). Выводом формулы решения квадратных уравнений общего вида занимался Виет. Формулы, выражающие зависимость корней уравнения от его коэффициентов, были выделены Виетом в 1591 г. Однако свое утверждение он высказывал лишь для положительных корней (отрицательных чисел он не признавал). После трудов нидерландского математика А. Жирара (1595-1632), а также Декарта и Ньютона способ решения квадратных уравнений принял современный вид.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Перечислим десять способов решения квадратных уравнений:
Решение квадратных уравнений по формуле корней
Квадратное уравнение – алгебраическое уравнение общего вида
где х - свободная переменная, a, b, c - коэффициенты, причём a ≠ 0.
Выражение a•x2 + b•x + c называют квадратным трёхчленом.
Корень - это значение переменной x, обращающее квадратный трёхчлен в ноль, а квадратное уравнение в верное равенство.
Элементы квадратного уравнения имеют собственные названия:
- называют первым или старшим коэффициентом,
- называют вторым, средним или коэффициентом при ,
- называют свободным членом.
Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент:
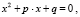
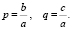
Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.
Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме старшего (либо второй коэффициент, либо свободный член), равен нулю.
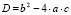
Квадратное уравнение с вещественными коэффициентами a, b cимеет ровно два комплексных корня, о чём гласит основная теорема алгебры. При этом, в зависимости от значения дискриминанта , как один, так и оба корня могут не иметь мнимой части и быть вещественными:
- при D > 0 вещественных корней два, и они вычисляются по формуле
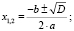
- при D = 0 корень один (о чём так же можно говорить как о двух равных или совпадающих корнях), кратности 2:
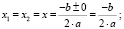
-
при D 0, то вычислить и напечатать значения x1 и x2 и перейти к п. 6. Иначе перейти к п. 4.
4. Если D = 0, то вычислить и напечатать значение x1 = x2 = x и перейти к п. 6. Иначе перейти к п. 5.
5. Вычислить действительную и мнимую части комплексных корней и напечатать значения пары комплексно сопряженных корней.
6. Прекратить вычисления.
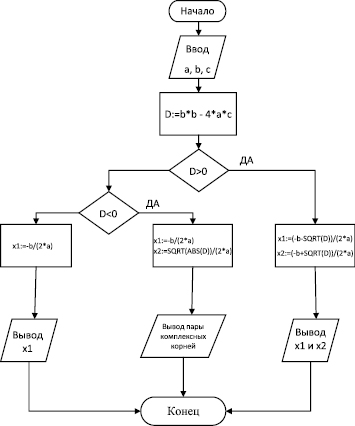
Представим разработанный выше алгоритм в виде блок-схемы.
Блок-схемой называется наглядное графическое изображение алгоритма, когда отдельные его этапы изображаются при помощи различных геометрических фигур – блоков, а связи между этапами (последовательность выполнения этапов) указываются при помощи стрелок, соединяющих эти фигуры. Блоки сопровождаются надписями. Типичные действия алгоритма изображаются геометрическими фигурами согласно ГОСТ 19.701-90.
Интегрированная среда программирования Паскаль-ABC. Разработка и тестирование программы
Наиболее распространенным в настоящее время языком программирования для компьютеров серии IBM PC является Паскаль. Это язык высокого уровня, отличающийся простотой синтаксиса, структурированный и удобный для начального обучения программированию.
Учебная система программирования Паскаль-ABC представляет собой диалект стандартного языка Паскаль. Система создавалась на факультете математики, механики и компьютерных наук ЮФУ как учебная среда программирования (автор - кандидат физико-математических наук, доцент кафедры алгебры и дискретной математики С.С. Михалкович).
Система Паскаль-ABC предназначена для обучения программированию на языке Паскаль и ориентирована на школьников и студентов младших курсов. По мнению разработчиков этой системы, первоначальное обучение программированию должно проходить в достаточно простых и дружественных средах, в то же время эти среды должны быть близки к стандартным и иметь богатые и современные библиотеки подпрограмм.
Система программирования Паскаль-ABC представляет собой единство компилятора языка программирования Паскаль и инструментальной программной оболочки, называемой средой. Среда предоставляет необходимые сервисные услуги и способствует повышению эффективности процессов разработки, отладки и испытаний программ, что облегчает труд программиста.
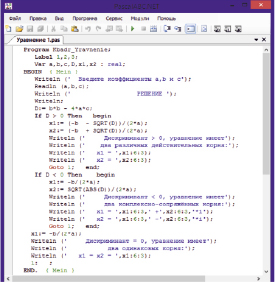
Рис. 2. Скриншот разработанной программы решения квадратных уравнений в среде Паскаль-ABC
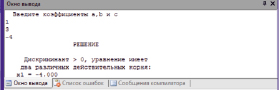
Рис. 3. Скриншот результата вычислений действительных различных корней
На рис. 2 представлен скриншот разработанной программы решения квадратных уравнений в среде Паскаль-ABC. Т.к. программа имеет три разветвления, то протестируем каждую из ветвей.
Решим квадратное уравнение, имеющее два действительных корня (D > 0):
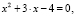
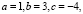
Здесь поэтому формула корней квадратного уравнения имеет вид:
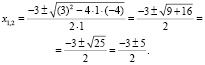
Тогда, вычисленные корни имеют вид:
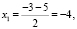
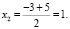
Скриншот полученного результата представлен на рис. 3.
Решим квадратное уравнение, имеющее один действительный корень (D = 0):
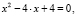
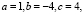
Здесь поэтому формула корней квадратного уравнения имеет вид:
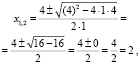
Скриншот полученного результата представлен на рис. 4.
Решим квадратное уравнение, имеющее пару комплексно сопряженных корней (D

Добрый день. Сегодня я хочу поделиться программой, написанной на языке программирования Паскаль, а именно исходник программы, которая находит корни квадратного уравнения.
Итак, задача звучит следующим образом:
"Составьте программу вычисления корней квадратного уравнения по данным значениям его коэффициентов".
Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:
Выбранный для просмотра документ Оценочный лист.docx
Оценочный лист ______________________
Выбранный для просмотра документ Презентация1.pptx

Описание презентации по отдельным слайдам:

Тема урока: Создание программ с ветвлениями. Программа для решения квадратных уравнений (По формуле квадратного уравнения)

Цель урока: информатика: закрепление умений в создании программ с ветвлениями закрепление навыков работы в среде программирования Паскаль; математика: закрепление навыков решения квадратных уравнений с помощью формул

Какие уравнения мы называем квадратными? ax2 + bx + c = 0 полное неполное b=0 ax2 + c = 0 c=0 ax2 + bx = 0 где a, b, c – некоторые числа (а≠0), Х - переменная

Какие способы решения квадратных уравнений вам известны? Теорема Виета Разложение на множители Общие формулы для решения квадратных уравнений

Повторим формулы для решения квадратных уравнений D = b2 - 4ac



Полная форма ветвления Неполная форма ветвления Да Нет Да Нет Блок-схема команды ветвления Действие 1 Условие Действие 2

Запись команды ветвления на языке Паскаль Полная форма If условие then begin оператор 1; оператор 2;… end else begin оператор 1; оператор 2;… end; Неполная форма If условие then begin оператор 1; оператор 2;… end;



Во время работы за ПК Во время работы на ЭВМ необходимо соблюдать оптимальное расстояние глаз от экрана (60-70 см). Допустимое расстояние -50 см. (рисунок 1) В случае возникновения зрительного напряжения или усталости можно, не вставая с места, выполнить несколько упражнений для снятия напряжения или усталости. ( упражнения для глаз) В случае необходимости оказать первую медицинскую помощь при электротравме, знать приемы работы с огнетушителем и приемы тушения пожара.

При аварийной ситуации При обнаружении дефектов ПК в процессе работы, появлении гари или необычных звуков необходимо немедленно прекратить работу на ПК, выключить аппаратуру и сообщить преподавателю. При необходимости следует оказать помощь в тушении огня. При необходимости уметь оказать первую доврачебную помощь пострадавшим от электрического тока. Необходимо знать, что нельзя тушить пожар в компьютерном классе водой. Можно использовать песок или пенный огнетушитель. Необходимо знать, что если пострадавший находится под воздействием электротока, то его нельзя трогать голыми руками. Освободить пострадавшего можно, используя материалы, которые не являются проводниками электрического тока.

После выполнения практической работы 1. По указанию преподавателя отключить аппаратуру. 2. Навести порядок на рабочем месте.


Ход работы Составить словесный алгоритм решения квадратного уравнения Составить блок-схему решения квадратного уравнения Составить программу на языке Паскаль Набрать программу в среде программирования Free Pasсal Протестировать программу Решить предложенные квадратные уравнения Записать ответы в оценочный лист В оценочном листе поставьте себе оценку за выполнение практической работы Записать вывод в тетрадь

Словесный алгоритм решения квадратного уравнения Находим дискриминант Сравниваем дискриминант D c нулем (если D 0, то два корня) 3. Находим корни квадратного уравнения, если они есть


Оценочный лист необходимо заполнить № задания D Корни (есть/нет) X1 X2 № 434 1) 2) 3) 4) 5) 6) № 436 1) 2) 3) 4) № 437 1) 2) 3)

Рефлексия Назовите тему урока Что было самым легким на уроке? Что было трудно? После урока у меня остались вопросы… Знания, полученные на уроке мне пригодятся для…

Домашнее задание Информатика § 3.4., упр.3, 4, 8; (2 упр. на выбор); Математика § 28
Выбранный для просмотра документ Урок.doc
Технологическая карта интегрированного урока математики и информатики
Практическая работа «Создание программ с ветвлениями.
Интегрированный (информатика + математика)
Обучающие цели
закрепление умений в создании программ с ветвлениями
закрепление навыков работы в среде программирования Паскаль
закрепление навыков решения квадратных уравнений с помощью формул
Развивающие цели
Учить устанавливать межпредметные связи.
1) формирование навыков самостоятельной работы и сотрудничества;
2) развитие аналитико-синтетических и рефлексивных умений.
Воспитательные цели
Создание условия для развития мотивации учения, формирование культуры учебной деятельности, воспитание дисциплинированности, требовательности к себе.
Формы обучения
Коллективная, фронтальная, индивидуальная
Методы обучения
Наглядный, практический, частично-поисковый
Межпредметные связи
Формирование темы и цели урока
Актуализация опорных знаний
5.1 инструктаж по ТБ
5.2 определение темы и цели практической работы
выполнение практической работы
Подведение итогов. Оценивание.
Домашнее задание. Комментарии к домашнему заданию
Задачи учителя на этапе
Содержание, методическое обеспечение
1. Организацион-ный этап
к работе на уроке
Готовность к уроку
(дневник, тетрадь, учебник, пенал)
Создание условий для благоприятной
психологической обстановки на уроке
2. Формирование темы и цели урока
Раскрытие темы и цели урока
Какую тему вы изучали на уроках математики ?
А на уроках информатики?
Как можно было бы использовать знания, полученные на этих уроках
Тогда темой нашего урока будет.
Как вы думаете, а какова цель нашего урока?
Учились решать квадратные уравнения
Учились составлять программы с ветвлениями
Составить программу для решения квадратных уравнений
Создание программы для решения квадратного уравнения
Научиться использовать знания, полученные на информатике для изучения других предметов





Создание программы решения уравнений второй и выше степени в системе Pascal ABC

Автор работы награжден дипломом победителя II степени
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF
Таким образом, актуальность исследования объясняется тем, что проблемы проверки решения уравнения порядка второго и выше остро стоят перед обучающимися, а решиться такие проблемы могут через совершенствования математических знаний и составления прикладных программ. В свою очередь эти знания могут применяться на практике для решения уравнений, что улучшит проверку знаний обучающихся и значительно сократит время на их решение.
Объектом исследования является схема Горнера, и система программирования Pascal ABC.
Предметом исследования выступают алгоритм Горнера для решения уравнений второго порядка и выше в системе программирования Pascal ABC.
Цель исследования – реализация решения уравнений второго и выше порядка, основываясь на схеме Горнера в среде программирования Pascal ABC.
Цель и предмет исследования обусловили необходимость решения следующих задач:
Исследовать важность данной проблемы у обучающихся 9 – 11 классов и выявить эффективность взаимосвязи математического алгоритма и системы программирования Pascal ABC.
Определить эффективность создания программы решения уравнений.
Оценить перспективы от создания программы.
Основу гипотезы исследования составили предположения о том, что если изучить схему Горнера, то найти решение для автоматического определения корней уравнения второго и выше порядка будет проще.
В процессе исследования использовались методы системного, математического и информационного анализа. В качестве информационной базы были использованы материалы, научные труды специалистов в области программирования, и справочные материалы, концепции, представленные в современной математике.
В ходе исследования были использованы следующие группы методов:
теоретические: теоретический анализ литературы по проблеме; систематизация полученной информации; обобщение выводов.
эмпирические: опросно – диагностические методы (интервьюирование, беседы) и др.;
статистические: анализ статистических данных.
Исследована важность проблемы и сравнены способы решения уравнений второго и выше порядка в различных источниках.
Определена эффективность создания программы решения уравнений второго и выше порядка в системе программирования Pascal ABC.
Оценены перспективы от создания программы.
Теоретическая значимость исследования состоит в разработке алгоритма решения уравнений второго и выше порядка при составлении программы на языке программирования Pascal ABC.
Практическая значимость выводов и рекомендаций, содержащихся в работе, связана с тем, что выполненное исследование направлено на решение конкретной задачи. Работа может быть использована также учителями, проверяющими решение уравнений различных порядков.
Теоретические выводы и практические рекомендации, полученные в результате исследования, могут быть использованы школьниками и учителями различных регионов при решении уравнений второго и выше порядка, а также при составлении программы решения уравнений.
Подготовительный (Подборка и изучение материала по данной теме, выделение проблем. Подборка вопросов для анкетирования)
Анкетирование (Анкетирование учащихся школы по разработанным анкетам)
Обработка анкет и анализ полученных результатов (Работа включает в себя выбор программного обеспечения для обработки анкет. Обработка данных и анализ результатов.)
Разработка алгоритма решения уравнений второго и выше порядка (На этом этапе на основе изученной литературы разрабатывается алгоритм решения уравнений второго и выше порядка.)
Составление и тестирование программы.
Презентация проекта (Представление итогового проекта для обсуждения и оценивания.)
Методы исследования. Анализ информационных источников, статистическая обработка результатов.
В настоящее время решение уравнений второго порядка и выше на практике в связи с масштабными затратами времени, выполнение повторных действий заставляет задуматься о составлении программы. В целях обеспечения эффективного решения проблем в области работы с цифрами, когда на любом этапе можно допустить вычислительные ошибки, необходимо создание программы, находящей корни уравнения для проверки собственного решения.
Различные уравнения решали более 25 веков назад. Множество способов решения таких уравнений были созданы в Вавилоне, Индии. Потребность в уравнениях была и будет. Нами приведены способы решения (нахождения корней) квадратных уравнений и уравнений высших степеней. Целое уравнение третьей или более высокой степени в отдельных случаях удается решить, используя точечные приемы. Один из приемов решения уравнения вида Р(х)=), где Р(х) – многочлен, степень которого больше двух, состоит в разложении многочлена на множители. Вспомним, какие способы разложения многочлена на множители мы изучали в 7 классе.
Вынесение общего множителя за скобки
С помощью формул сокращенного умножения
С помощью корней квадратного трехчлена.
1.1. Схема Горнера. Возможности.
В этой части нами рассмотрено решения уравнений второго и выше порядка по схеме Горнера. Большинство этих формул решения уравнений частного характера. Эти свойства очень удобны так, как гораздо легче решать уравнения по отдельной формуле для этого уравнения, а не по общему принципу. К каждому из способов мы рассмотрели несколько примеров.
Уильям Джордж Горнер (1786 – 1837), известный по схеме Горнера. Опубликована теорема была в 1815г. в Англии.
Схема Горнера позволяет:
Найти значение многочлена в точке a;
Выяснить, является ли число a – корнем многочлена;
Найти новый многочлен от деления на двучлен (понизить степень);
Используя схему Горнера, мы одновременно проверяем, является ли числоa корнем многочлена и делим этот многочлен на двучлен . Это нам потребуется для понижения степени уравнения и мы сможем воспользоваться вспомогательным алгоритмом.
Выделим существенные правила, которые нам могут пригодиться при решении уравнений второго и выше порядка. Здесь нам помогут такие факты:
Если сумма всех коэффициентов многочлена равна нулю, то число 1 является корнем многочлена.
Если сумма коэффициентов многочлена при четных степеняхравна сумме коэффициентов при нечетных степенях, то число -1 является корнем многочлена.
Для приведенного многочлена степени (из теоремы Виета следует, что) если корни многочлена целые, то они являются делителями его свободного члена, который также является целым числом.
Вывод: Исходя из этого, нам надо разложить свободный член многочлена на множители, и последовательно, от меньшего к большему, проверять, какой из множителей является корнем многочлена. Рассмотрим виды уравнений и вычислим корни.
1.2. Виды уравнений. 1.2.1. Уравнения второй степени (квадратные)
Квадратное уравнение - алгебраическое уравнение 2 - й степени. Общий вид уравнения: . Корни уравнения : Формулы верны при любых коэффициентах.
1.2.2. Уравнения третьей степени (кубические)
Кубическое уравнение - алгебраическое уравнение третьей степени. Общий вид кубического уравнения: ax 3 + bx 2 + cx + d = 0, где а ≠ 0
Используя правила Горнера решим уравнение такого вида. (Приложение 2). Понизив степень многочлена мы продолжаем решение обычного квадратного уравнения, рассмотренного ранее.
1.2.3. Уравнения четвертой степени
Уравнение четвертой степени - алгебраическое уравнение четвертой степени. Общий вид кубического уравнения: аx 4 + bx 3 + cx 2 + dх+е = 0,где а ≠ 0.
Используя схему Горнера решим уравнение этого вида.(Приложение 3). Понизив степень многочлена мы продолжаем решение кубического уравнения, используя схему Горнера, поставив перед собой цель, понизить степень до квадратного уравнения.
В теоретической части нашей работы нами рассмотрены решение квадратных уравнений и уравнений третьей, четвертой степени методом Горнера, определена схема решения уравнений второго, третьего, четвертого порядка, выведены новые, ранее нам неизвестные формулы. Мы проработали много вариантов примеров перед тем, как сделать вывод: используя схему Горнера, мы решаем уравнения третьей, четвертой и выше степеней аналогично. Мы уже представляем себе, как составить программу , которая будет решать уравнения такого вида. Каждое решение пригодится нам в дальнейшей учебе. Эта работа помогла классифицировать старые знания и познать новые.
Цель: проанализировать основные методы решения уравнений на практике; проанализировать время, которое тратится на решение уравнений второй и выше степени.
Для того чтобы грамотно реализовать собственную программу, необходимо не только ознакомится с мнением, решением, ошибками других, и понять причины, по которым они произошли, но и, возможно, применять особые приемы программирования и специализированные средства разработки.
По результатам анкетирования (приложение 1) учащихся 9 – 11 классов (всего 55 оппонентов) оценки правильного нахождения корней уравнений второго и выше порядка выделено:
Время, которое затрачивается обучающимся на решение уравнений:
Из графика видно, что временные затраты на решение даже одного уравнения существенно. А если их надо решить несколько? Время увеличится в разы.
2.2. Эксперимент 2. Создание алгоритма решения уравнений второго порядка и выше.
Цель: проанализировать эффективность метода Горнера при составлении программы; выработать схему использования вспомогательного алгоритма.
Проанализировав анкеты, мы выяснили, что при решении уравнений второго и выше пличными методами: методом подбора корней, делением уголочком многочлена на многочлен, что довольно долгий процесс решения.
Рассмотренные теоретические вопросы дают возможность создания алгоритма решения поставленной цели. Этот алгоритми будем разрабатывать.
Цель: составить программу, позволяющую решать уравнения второй и выше степени; проанализировать работу программы.
Для составления программы мы выбрали среду программирования Pascal ABC. Данная программная среда является языком высокого уровня и в последнее время пользуется не только профессиональными программистами, но и начинающим, а также на уроках информатике и ИКТ в гимназии.
В системе программирования четко реализованы принципы структурного программирования. Сначала мы написали программы отдельно для каждого вида уравнений. Затем воспользовались вспомогательным алгоритмом нахождения квадратного уравнения (приложение 3), кубического уравнения (приложение 4), решили объединить, составили программу с использованием процедуры. Рассмотренные теоретические вопросы дают возможность создания программы на Pascal ABC для решения.
Текст программы решения уравнений второй и выше степени, приведен в приложении 5.
В данной главе рассмотрен алгоритм решения уравнений с использованием схемы Горнера. Составленная программа решения уравнений второй и выше степени может быть использована в практической деятельности для помощи учащимся и учителям решать и проверять соответственно задания , где требуется нахождения корней уравнений второй, третьей, четвертой степени , значительно сократив время на проверку.
Математическая энциклопедия. — М.: Советская энциклопедия.И. М. Виноградов.1977—1985.
Приложение 1 Анкета для обучающихся
Умеете ли Вы решать уравнения вида ах 2 + вх+с=0 (уравнения второго порядка)?
в) никогда не делал этого ( не встречал в своей жизни)
Сколько занимает времени решение одного уравнения второго порядка?
а) от 1 до 5 минут б) от 5до 10 минут
в) от 10 до 30 минут г) около часа
Умеете ли Вы решать уравнения вида ах 3 + вх 2 +сх+d=0 (уравнения третьего порядка)?
в) никогда не делал этого ( не встречал в своей жизни)
Сколько занимает времени решение одного уравнения третьего порядка?
а) от 1 до 5 минут б) от 5до 10 минут
в) от 10 до 30 минут г) около часа
Умеете ли Вы решать уравнения вида ах 4 + вх 3 +сх 2 +dx+e=0 (уравнения четвертого порядка)?
в) никогда не делал этого ( не встречал в своей жизни)
Сколько занимает времени решение одного уравнения четвертого порядка ?
а) от 1 до 5 минут б) от 5до 10 минут
в) от 10 до 30 минут г) около часа
Умеете ли Вы решать уравнения более высокого порядка ?
в) никогда не делал этого ( не встречал в своей жизни)
Хотели бы Вы научиться решать уравнения второго порядка и выше?
а) да б) нет в) предпочитаю списать
Хотели бы Вы иметь у себя программу, решающую уравнения второго порядка и выше?
Читайте также:


