Как сделать ряд стационарным python
Как я могу генерировать последовательность чисел "1,2,5,6,9,10. "и так до 100 в Python? Мне даже нужна запятая ( ' ,'), но это не главная проблема.
последовательность: каждое число от 1..100, делятся на 4 с остатком 1 или 2.
каждое число от 1,2,5,6,9,10. делится на 4 с остатком 1 или 2.
Это было быстрое и довольно грязное решение.
Теперь, для решения, которое подходит для различных видов проблем прогрессии:
и вот аналогичные идеи, реализованные с помощью itertools:
включает в себя некоторые догадки о точной последовательности, которую вы ожидаете:
(кстати. это Python 3 совместимый)
С помощью NumPy и понимание списка вы можете сделать
это работает, используя свойства % списка, а не приращения.
предполагая, что я правильно угадал шаблон (чередующиеся приращения 1 и 3), это должно привести к желаемому результату:
предполагая, что ваша последовательность чередуется с шагом от 1 до 3
Это может быть проще изменить, если ваша последовательность отличается, но я думаю, что poke или BlaXpirit-более приятные ответы, чем мои.
в python 3.1 вы можете создать список способом
в Python 2.7 вы можете сделать это
написать функцию, которая принимает число в качестве аргумента и выводит ряд Фибоначчи до этого числа
Комментарий может занимать всю строчку:
или может находиться на строчке после какого-нибудь кода:
Внимание: любую строку можно превратить в комментарий, достаточно в начале строки набрать комбинацию клавиш Ctrl+/
Числа
Числа в Python бывают трёх типов:
Строки
Строка – это последовательность символов. Чаще всего строки – это просто некоторые наборы слов. Слова могут быть как на английском языке, так и почти на любом языке мира.
Кавычки
Строку можно указать, используя одинарные кавычки, как например, 'Это строка'. Любой одиночный символ в кавычках, например, 'ю' — это строка. Пустая строка '' — это тоже строка. То есть строкой мы считаем всё, что находится внутри кавычек.
Запись строки в одинарных кавычках это не единственный способ. Можно использовать и двойные кавычки, как например, ''Это строка''. Для интерпретатора разницы между записями строки в одинарных и двойных кавычках нет.
Внимание :
Если строка началась с двойной кавычки — значит и закончиться должна на двойной кавычке.
Если внутри строки мы хотим использовать двойные кавычки, то саму строку надо делать в одинарных кавычках.
Театр '' Современник ' '
print ('Театр '' Современник '' ')
Строка, занимающая несколько строк, должна быть обрамлена тройными кавычками ( '' '' '' или ''' ). Например:
'''В Python можно использовать одинарные,
двойные и тройные кавычки,
чтобы обозначить строку'''
Отступы
Сдвиг строки с помощью пробелов называется отступами .
Оператор присваивания
Переменная – это именованная область памяти, в которой хранятся данные. Данные помещаются в эту область памяти, как в ящик, с помощью оператора присваивания. Общая форма записи операции присваивания:
Знакомый нам знак равно (=) в программирование это знак операции присваивания. Различие между знаками равно и присваивания в следующем.
Например:
В обычной математической записи выражение b (рано) = b + 2 является не верным. Однако запись оператора присваивания b (присвоить) = b + 2 правильная и означает следующее: к текущему значению переменной b, например, оно было равно 4, прибавляется число 2 , и после выполнения данного оператора, значение переменной будет равно 6.
Основные операторы
Оператор
Краткое описание
Сложение (сумма x и y)
Вычитание (разность x и y)
Умножение (произведение x и y)
Внимание! Если x и y целые, то результат всегда будет целым числом! Для получения вещественного результата хотя бы одно из чисел должно быть вещественным. Пример: 40/5 → 8, а вот 40/5.0 → 8.0
y+=x; эквивалентно y = y + x;
y-=x; эквивалентно y = y - x;
y*=x; эквивалентно y = y * x;
y/=x; эквивалентно y = y / x;
y%=x; эквивалентно y = y % x;
больше или равно
меньше или равно
Деление по модулю - деление, в котором возвращается остаток.
4 % 2 в результате будет 0
5 % 2 в результате будет 1
Целочисленное деление - деление, в котором возвращается целая часть результата. Часть после запятой отбрасывается
4 // 3 в результате будет 1
25 // 6 в результате будет 4
Возведение в степень
5 ** 2 в результате будет 25
логическое отрицание НЕ
Основные типы данных
Имя
Тип
Описание
int
float
str
Последовательность символов: " abc " , " pyhton " , " 123 "
list
Последовательность объектов: [ 1, 2.0, " Привет! " ]
dist
tuple
Последовательность неизменных объектов:(20,25 )
set
Последовательность уникальных объектов:
bool
Логические значения: True или False
Список
Список (list) представляет тип данных, который хранит набор или последовательность элементов.
Для создания списка в квадратных скобках [ ] через запятую перечисляются все его элементы.
Создание пустого списка
Создание списка чисел:
Создание списка слов:
Создание списка из элементов разного типа
Для управления элементами списки имеют целый ряд методов. Некоторые из них:
Кроме того, Python предоставляет ряд встроенных функций для работы со списками:
Генераторы
Для создания списков, заполненных по более сложным формулам можно использовать генераторы: выражения, позволяющие заполнить список значениями, вычисленными по некоторым формулам.
Общий вид генератора следующий :
Прим ер. Создать список чисел от 0 до 10
[ i for i in range ( 0 , 10 )]
Вся конструкция заключается в квадратные скобки, потому что будет создан список. Внутри квадратных скобок можно выделить три части:
1) что делаем с элементом i : просто добавляем значение i в список
2) что берем: берем i
3) откуда берем : из объекта range .
Части отделены друг от друга ключевыми словами for и in .
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
Пример . Создать список заглавных букв английского алфавита. Код символа ' A ' – 65, код символа ' Z ' – 91. Поскольку символы идут подряд, то возможно использовать генератор.
что делаем: к значению элемента i применяем функцию chr ( i ).
Внимание. Функция chr ( i ) – по числовому коду символа возвращает сам символ. Пример. chr (65) даст символ ' A '.
['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z']
Пример. Создать список строчный букв английского алфавита. Код символа 'a' – 97, код символа 'z' – 123. Поскольку символы идут подряд, то возможно использовать генератор.
['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z']
Библиотека math
Для проведения вычислений с действительными числами язык Python содержит много дополнительных функций, собранных в библиотеку, которая называется math . Для использования этих функций в начале программы необходимо подключить библиотеку, что делается командой
После подключения программа получает доступ ко всем функциям, методам и классам, содержащимся в нём. После подключения можно вызвать любую функцию из подключенной библиотеки по следующему правилу: указывается имя модуля и через точку имя функции
Можно подключать не весь модуль, а какую-то его часть. Например, программист хочет использовать только одну функцию из математической библиотеки math . Если он подключит всю библиотеку, то будет добавлено более 40 функций, которые будут занимать место. Чтобы добавить в проект какую-то часть, используют ключевое слово from :
Ниже приведен список основных функций модуля math . Некоторые из перечисленных функций ( int , round , abs ) являются стандартными и не требуют подключения модуля math для использования.
Функция
Описание
Округление
int(x)
Округляет число в сторону нуля. Это стандартная функция, для ее использования не нужно подключать модуль math .
round(x)
Округляет число до ближайшего целого. Если дробная часть числа равна 0.5, то число округляется до ближайшего четного числа.
round(x, n)
Округляет число x до n знаков после точки. Это стандартная функция, для ее использования не нужно подключать модуль math .
floor(x)
ceil(x)
abs(x)
Модуль (абсолютная величина). Это — стандартная функция.
Корни, логарифмы
sqrt(x)
Квадратный корень. Использование : sqrt(x)
log(x)
Натуральный логарифм. При вызове в виде log(x, b) возвращает логарифм по основанию b .
e
Основание натуральных логарифмов e = 2,71828.
Тригонометрия
sin(x)
Синус угла, задаваемого в радианах
cos(x)
Косинус угла, задаваемого в радианах
tan(x)
Тангенс угла, задаваемого в радианах
asin(x )
Арксинус, возвращает значение в радианах
acos(x)
Арккосинус, возвращает значение в радианах
atan(x)
Арктангенс, возвращает значение в радианах
atan2(y, x)
Полярный угол (в радианах) точки с координатами (x, y).
degrees(x)
Преобразует угол, заданный в радианах, в градусы.
radians(x)
Преобразует угол, заданный в градусах, в радианы.
pi
Константа π = 3.1415.
Генерация случайных чисел (модуль random)
Python порождает случайные числа на основе формулы, так что они на самом деле не случайные, а, как говорят, псевдослучайные.
Модуль random позволяет генерировать случайные числа и имеет большое множество важных для практики функций. Рассмотрим основные функции:
Функция random . random () случайное число от 0 до 1.

При создании коллекций элементов на Python циклы for заменяются однострочными выражениями. Python поддерживает четыре типа особенных генераторов, называемых также включениями:
- Списковые включения (генераторысписков, Listcomps).
- Словарные включения (генераторы словарей, Dictcomps).
- Множественные включения (генераторы множеств, Setcomps).
- Генераторные выражения (GenExp).
Синтаксис генератора списков устроен следующим образом:
Часть с условием if указывается опционально.
Пример
Давайте создадим список чисел, исключив из него все отрицательные значения — для начала решим задачу с помощью обычного цикла for :
Для быстрого, лаконичного и наглядного создания словарей язык программирования Python предлагает воспользоваться специальным сокращением для циклического перебора элементов, известным как “генератор словарей”.
Синтаксис генератора словарей устроен следующим образом:
Пример
Давайте возведем в квадрат все числовые значения словаря при помощи словарного включения:
Генератор множества одновременно похож на словарное включение и на списковое включение: фигурные скобки, как у словарей, остальной синтаксис выражения — как у списков. Основное отличие генератора множеств от словарного включения заключается в том, что для генерации словаря указываются ключ и значение через двоеточие, а для генерации множества — одно только значение.
Синтаксис генератора множеств устроен следующим образом:
Пример
Давайте создадим список произвольных чисел и множество парных чисел на его основе:
При помощи генератора множеств подобная программа пишется в одну строчку:
Подобно включениям, выражение генератора предлагает сокращенный синтаксис для цикла for .
Синтаксис генераторных выражений следующий:
Пример
Давайте возведем в квадрат все четные числа списка и отбросим все нечетные.
Для начала решим задачу с помощью обычного цикла for :
С помощью выражения-генератора можно вообще забыть о потребности в функции square_even() и сделать то же самое с помощью одной строки кода:
При взгляде на синтаксис генераторных выражений, сразу же в голову приходит мысль: как написать кортежное включение?
Генераторное выражение можно передавать в качестве параметра любой функции-конструктору стандартных типов данных Python:
Только что вы узнали о четырех типах генераторов последовательностей в Python.
Теперь важно научиться избегать соблазна заменить все циклы for в ваших проектах на включения: давайте обсудим, в каких случаях генераторы последовательностей не подходят.
Короче говоря, не используйте включения, когда они снижают качество вашего кода!
Хороший пример — это работа со вложенными циклами for . Если написать вложенный цикл for в виде включения, то код станет короче на несколько строк, но его качество рискует ухудшиться.
Давайте рассмотрим матрицу; она часто представляется в Python как список из списков. Если вы хотите отобразить матрицу в одном измерении, то можете применить двойное списковое включение:
Код лаконичен, но, возможно, не так интуитивно понятно, что он делает: если вместо включения написать вложенный цикл for, то программа сразу станет более понятным:
Наконец, давайте посмотрим на производительность включений в сравнении с обычным циклом for :

Аналогичный бенчмарк для генераторов множеств и словарей дает схожие результаты: включение работает немного быстрей.
Для генераторных выражений сравнение с циклом for + yield бессмысленно: оба возвращают объект-генератор почти мгновенно. Время не тратится на вычисление значений, поскольку генераторы не хранят значения.
Следовательно, не стоит универсально везде применять включения для повышения производительности программ. Выигрыш в скорости выполнения незначителен по сравнению с вредом, наносимым длинными и многословными включениями. Применяйте генераторы последовательностей только тогда, когда это очистит ваш код без снижения его качества.
Включения превращают циклы for в однострочные выражения.
Python поддерживает четыре вида включений для стандартных структур данных:
- Списковые включения.
- Словарные включения.
- Множественные включения.
- Генераторные выражения.
Разумное применение включений улучшает качество вашего кода, но откажитесь от слепой замены всех циклов на выражения, ведь иногда замена вложенного цикла for на включение снижает понятность кода.
Включения выполняются быстрее, чем цикл for , однако разница — всего 10%, поэтому вместо производительности отдавайте предпочтение качеству кода.

Для примера можно взять сотрудников какой-нибудь компании и понять, как значение зарплаты зависит от других данных, таких как опыт работы, уровень образования, роль, город, в котором они работают, и так далее.
Регрессия решает проблему единого представления данных анализа для каждого работника. Причём опыт, образование, роль и город – это независимые переменные при зависимой от них зарплате.
Таким же способом можно установить математическую зависимость между ценами домов в определённой области, количеством комнат, расстоянием от центра и т. д.
Регрессия рассматривает некоторое явление и ряд наблюдений. Каждое наблюдение имеет две и более переменных. Предполагая, что одна переменная зависит от других, вы пытаетесь построить отношения между ними.
Другими словами, вам нужно найти функцию, которая отображает зависимость одних переменных или данных от других.
Зависимые данные называются зависимыми переменными, выходами или ответами.
Независимые данные называются независимыми переменными, входами или предсказателями.
Общей практикой является обозначение данных на выходе – ?, входных данных – ?. В случае с двумя или более независимыми переменными, их можно представить в виде вектора ? = (?₁, …, ?ᵣ), где ? – количество входных переменных.
Регрессия полезна для прогнозирования ответа на новые условия. Можно угадать потребление электроэнергии в жилом доме из данных температуры, времени суток и количества жильцов.
Где она вообще нужна?
Регрессия используется во многих отраслях: экономика, компьютерные и социальные науки, прочее. Её важность растёт с доступностью больших данных.
Линейная регрессия – одна из важнейших и широко используемых техник регрессии. Эта самый простой метод регрессии. Одним из его достоинств является лёгкость интерпретации результатов.
Постановка проблемы
Линейная регрессия некоторой зависимой переменной y на набор независимых переменных x = (x₁, …, xᵣ), где r – это число предсказателей, предполагает, что линейное отношение между y и x: y = 𝛽₀ + 𝛽₁x₁ + ⋯ + 𝛽ᵣxᵣ + 𝜀. Это уравнение регрессии. 𝛽₀, 𝛽₁, …, 𝛽ᵣ – коэффициенты регрессии, и 𝜀 – случайная ошибка.
Линейная регрессия вычисляет оценочные функции коэффициентов регрессии или просто прогнозируемые весы измерения, обозначаемые как b₀, b₁, …, bᵣ. Они определяют оценочную функцию регрессии f(x) = b₀ + b₁x₁ + ⋯ + bᵣxᵣ. Эта функция захватывает зависимости между входами и выходом достаточно хорошо.
Для каждого результата наблюдения i = 1, …, n, оценочный или предсказанный ответ f(xᵢ) должен быть как можно ближе к соответствующему фактическому ответу yᵢ. Разницы yᵢ − f(xᵢ) для всех результатов наблюдений называются остатками. Регрессия определяет лучшие прогнозируемые весы измерения, которые соответствуют наименьшим остаткам.
Для получения лучших весов, вам нужно минимизировать сумму остаточных квадратов (SSR) для всех результатов наблюдений: SSR = Σᵢ(yᵢ − f(xᵢ))². Этот подход называется методом наименьших квадратов.
Простая линейная регрессия
Простая или одномерная линейная регрессия – случай линейной регрессии с единственной независимой переменной x.
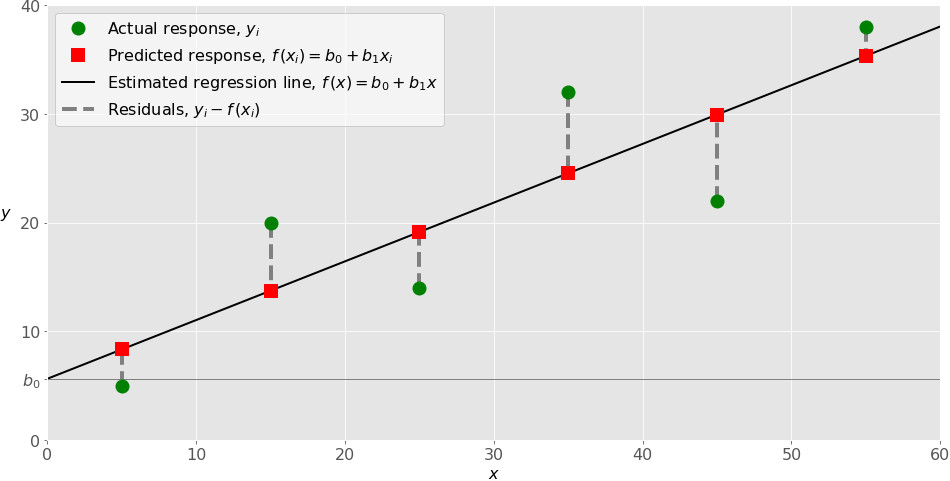
Реализация простой линейной регрессии начинается с заданным набором пар (зелёные круги) входов-выходов (x-y). Эти пары – результаты наблюдений. Наблюдение, крайнее слева (зелёный круг) имеет на входе x = 5 и соответствующий выход (ответ) y = 5. Следующее наблюдение имеет x = 15 и y = 20, и так далее.
Оценочная функция регрессии (чёрная линия) выражается уравнением f(x) = b₀ + b₁x. Нужно рассчитать оптимальные значения спрогнозированных весов b₀ и b₁ для минимизации SSR и определить оценочную функцию регрессии. Величина b₀, также называемая отрезком, показывает точку, где расчётная линия регрессии пересекает ось y. Это значение расчётного ответа f(x) для x = 0. Величина b₁ определяет наклон расчетной линии регрессии.
Предсказанные ответы (красные квадраты) – точки линии регрессии, соответствующие входным значениям. Для входа x = 5 предсказанный ответ равен f(5) = 8.33 (представленный крайним левыми квадратом).
Остатки (вертикальные пунктирные серые линии) могут быть вычислены как yᵢ − f(xᵢ) = yᵢ − b₀ − b₁xᵢ для i = 1, …, n. Они представляют собой расстояния между зелёными и красными пунктами. При реализации линейной регрессии вы минимизируете эти расстояния и делаете красные квадраты как можно ближе к предопределённым зелёным кругам.
Пришло время реализовать линейную регрессию в Python. Всё, что вам нужно, – подходящие пакеты, функции и классы.
Пакеты Python для линейной регрессии
NumPy – фундаментальный научный пакет для быстрых операций над одномерными и многомерными массивами. Он облегчает математическую рутину и, конечно, находится в open-source.
Незнакомы с NumPy? Начните с официального гайда.
Пакет scikit-learn – это библиотека, широко используемая в машинном обучении. Она предоставляет значения для данных предварительной обработки, уменьшает размерность, реализует регрессию, классификацию, кластеризацию и т. д. Находится в open-source, как и NumPy.
Начните знакомство с линейными моделями и работой пакета на сайте scikit-learn.
Простая линейная регрессия со scikit-learn
Начнём с простейшего случая линейной регрессии.
Следуйте пяти шагам реализации линейной регрессии:
- Импортируйте необходимые пакеты и классы.
- Предоставьте данные для работы и преобразования.
- Создайте модель регрессии и приспособьте к существующим данным.
- Проверьте результаты совмещения и удовлетворительность модели.
- Примените модель для прогнозов.
Это общие шаги для большинства подходов и реализаций регрессии.
Шаг 1: Импортируйте пакеты и классы
Первым шагом импортируем пакет NumPy и класс LinearRegression из sklearn.linear_model :
Теперь у вас есть весь функционал для реализации линейной регрессии.
Фундаментальный тип данных NumPy – это тип массива numpy.ndarray . Далее под массивом подразумеваются все экземпляры типа numpy.ndarray .
Класс sklearn.linear_model.LinearRegression используем для линейной регрессии и прогнозов.
Шаг 2 : Предоставьте данные
Теперь у вас два массива: вход x и выход y. Вам нужно вызвать .reshape() на x, потому что этот массив должен быть двумерным или более точным – иметь одну колонку и необходимое количество рядов. Это как раз то, что определяет аргумент (-1, 1).
Вот как x и y выглядят теперь:
Шаг 3: Создайте модель
На этом шаге создайте и приспособьте модель линейной регрессии к существующим данным.
Давайте сделаем экземпляр класса LinearRegression , который представит модель регрессии:
Эта операция создаёт переменную model в качестве экземпляра LinearRegression . Вы можете предоставить несколько опциональных параметров классу LinearRegression :
- fit_intercept – логический ( True по умолчанию) параметр, который решает, вычислять отрезок b₀ ( True ) или рассматривать его как равный нулю ( False ).
- normalize – логический ( False по умолчанию) параметр, который решает, нормализовать входные переменные ( True ) или нет ( False ).
- copy_X – логический ( True по умолчанию) параметр, который решает, копировать ( True ) или перезаписывать входные переменные ( False ).
- n_jobs – целое или None (по умолчанию), представляющее количество процессов, задействованных в параллельных вычислениях. None означает отсутствие процессов, при -1 используются все доступные процессоры.
Наш пример использует состояния параметров по умолчанию.
Пришло время задействовать model . Сначала вызовите .fit() на model :
С помощью .fit() вычисляются оптимальные значение весов b₀ и b₁, используя существующие вход и выход (x и y) в качестве аргументов. Другими словами, .fit() совмещает модель. Она возвращает self - переменную model . Поэтому можно заменить две последние операции на:
Эта операция короче и делает то же, что и две предыдущие.
Шаг 4: Получите результаты
После совмещения модели нужно убедиться в удовлетворительности результатов для интерпретации.
Вы можете получить определения (R²) с помощью .score() , вызванной на model :
.score() принимает в качестве аргументов предсказатель x и регрессор y, и возвращает значение R².
model содержит атрибуты .intercept_ , который представляет собой коэффициент, и b₀ с .coef_ , которые представляют b₁:
Код выше показывает, как получить b₀ и b₁. Заметьте, что .intercept_ – это скаляр, в то время как .coef_ – массив.
Примерное значение b₀ = 5.63 показывает, что ваша модель предсказывает ответ 5.63 при x, равном нулю. Равенство b₁ = 0.54 означает, что предсказанный ответ возрастает до 0.54 при x, увеличенным на единицу.
Заметьте, что вы можете предоставить y как двумерный массив. Тогда результаты не будут отличаться:
Как вы видите, пример похож на предыдущий, но в данном случае .intercept_ – одномерный массив с единственным элементом b₀, и .coef_ – двумерный массив с единственным элементом b₁.
Шаг 5: Предскажите ответ
Когда вас устроит ваша модель, вы можете использовать её для прогнозов с текущими или другими данными.
Получите предсказанный ответ, используя .predict() :
Применяя .predict() , вы передаёте регрессор в качестве аргумента и получаете соответствующий предсказанный ответ.
Вот почти идентичный способ предсказать ответ:
В этом случае вы умножаете каждый элемент массива x с помощью model.coef_ и добавляете model.intercept_ в ваш продукт.
Вывод отличается от предыдущего примера количеством измерений. Теперь предсказанный ответ – это двумерный массив, в отличии от предыдущего случая, в котором он одномерный.
Измените количество измерений x до одного, и увидите одинаковый результат. Для этого замените x на x.reshape(-1) , x.flatten() или x.ravel() при умножении с помощью model.coef_ .
На практике модель регрессии часто используется для прогнозов. Это значит, что вы можете использовать приспособленные модели для вычисления выходов на базе других, новых входов:
Здесь .predict() применяется на новом регрессоре x_new и приводит к ответу y_new . Этот пример удобно использует arange() из NumPy для генерации массива с элементами от 0 (включительно) до 5 (исключительно) – 0, 1, 2, 3, и 4.
Читайте также:


