Попадает ли точка в заштрихованную область excel
В задачах этого вида дан рисунок координатной плоскости, и некоей закрашенной/заштрихованной области, ограниченной набором прямых и кривых. Нужно определить, принадлежит ли точка с координатами (x,y) этой области или нет.
Так как уравнения всех границ указаны на графике, задачи этого вида требуют понимания того, какой знак нужно поставить в соответствующем неравенстве. плоскость бейсик паскаль программа
Выписав все неравенства, которые "ограничивают" закрашенную/заштрихованную область, и объединив их логической операцией «И» («AND»), получим условие, которое должна проверять программа. Если условие выполняется - точка принадлежит области, если не выполняется - не принадлежит.
Так, если искомую область ограничивает вертикальная прямая линия, то в общем виде уравнение этой прямой выглядит как
где а - то значение на оси х, через которое проходит данная прямая (напомним, что если эта прямая совпадает с осью у, то уравнение прямой будет "х=0").
Так как ось х направлена вправо (на что указывает "стрелка"), то все значения координаты x справа от нашей прямой будут больше числа а. А все значения координаты х слева от нашей прямой ("х=а") будут меньше а. Получаем, что если закрашенная/заштрихованная область лежит справа от прямой "х=а", то все ее точки удовлетворяют условию "х>=а", а если слева - то условию "х<=а".
Замечание относительно нестрогого неравенства (почему нужно писать именно "x>=a v вместо "х>а"): так как на графике все прямые и кривые нарисованы сплошной линией, то закрашенная/заштрихованная область включает свои границы. Поэтому мы и пишем "больше или равно" или "меньше или равно". Строгие неравенства (строго больше/меньше) нужно было бы использовать, если бы границы области были бы нарисованы пунктиром.
Все остальные прямые и кривые, ограничивающие область, уравнения которых сводятся к виду "у=какое-то_выражение" нужно рассматривать с позиции у-координаты (ведь это именно она стоит в левой части уравнения). Так как ось "у" направлена вверх, то все точки, которые лежат выше прямой/кривой, должны удовлетворять условию "у>=это_выражение", а все точки, лежащие ниже нее- условию "у<=это_выражение". Значит, если закрашенная/заштрихованная область лежит выше рассматриваемой прямой/кривой, то все ее точки удовлетворяют условию "у>=это_выражение", а если ниже - то условию " у<=это_выражение".
Напомним, что если нужная вам прямая горизонтальна, то ее уравнение имеет вид
где b - то значение на оси у, через которое проходит эта прямая. И, конечно, если прямая совпадает с осью х, то ее уравнение имеет вид "у=0".
Вывод уравнения прямой, наклонной к оси х выходит за рамки данной книги. На ЕГЭ по информатике вам это умение не понадобится, т.к. это уравнение будет явно указано на графике. А если вам это интересно для общего развития - полистайте учебник алгебры за предыдущие годы.
Единственный и особый случай, который мы хотели бы рассмотреть и напомнить вам - когда закрашенную/заштрихованную область ограничивает окружность. Если ее центр совпадает с началом координат, то уравнение точек на окружности имеет вид
где R - радиус этой окружности.
Как вы, вероятно, понимаете, левая часть этого уравнения (х 2 +у 2 ) задает квадрат расстояния от начала координат до точки плоскости. Для всех точек нашей окружности это расстояние равно ее радиусу R. Именно в этом смысл уравнения окружности. Значит, для всех точек внутри окружности, включая саму окружность, это расстояние будет меньше R. Это можно выразить неравенством
А для всех точек снаружи окружности неравенство будет "x 2 +y 2 >R 2 ". Рассмотрим пример:

В данной задаче закрашенную область ограничивают три прямые линии: горизонтальная (ее уравнение "у=2"), наклонная (ее уравнение "у=х") и вертикальная (она совпадает с осью у, ее уравнение "х=0").
Относительно горизонтальной прямой закрашенная область находится снизу, поэтому знак неравенства должен быть "меньше или равно" - "у<=2".
Относительно наклонной прямой закрашенная область находится сверху, поэтому знак неравенства должен быть "больше или равно" - "у>=х".
Относительно вертикальной прямой закрашенная область находится справа, поэтому знак неравенства должен быть "больше или равно" - "x>=0".
Итого получаем условие:
на Паскале и на Бейсике:
На Бейсике и Си, в данном случае, скобки можно не писать. Но лучше приучиться писать их всегда, чтобы не задумываться каждый раз, нужны они или нет.
В этом примере задача была очень простой - закрашенная область была ограничена только прямыми линиями. Если же область ограничена кривыми (или хотя бы одной кривой), то в список условий обычно приходится добавить еще одно или два условия- ведь кривая может в стороне от закрашенной области изменять свое направление.
И тогда получится, что набора ограничений, который мы написали, просто перечислив линии, ограничивающие область, может оказаться недостаточно. Рассмотрим пример:

Линий, ограничивающих закрашенную область, три: вертикальная прямая х=1,5, горизонтальная прямая у=0 и кривая у=х 2 .
Руководствуясь вышеприведенными рассуждениями, строим систему условий:
х<=1.5 (закрашенная область лежит левее вертикальной прямой), y>=0 (закрашенная область лежит выше горизонтальной прямой) и у<=x 2 (закрашенная область лежит ниже кривой).
Однако, этих условий недостаточно, чтобы ограничить закрашенную область.
Например, чтобы это понять, можно воспользоваться методом "штриховки": для каждого условия заштрихуем разными способами область плоскости, удовлетворяющую этому условию. Там, где все штриховки пересекутся (наложатся одна на другую), все условия будут выполняться.

На рисунке видно, что все три штриховки накладываются друг на друга не только на закрашенной области, но и в области, на которую указывает пунктирная стрелка. Этот эффект объясняется очень просто - правило, которое позволяет задать область плоскости, просто перечислив уравнения ограничивающих линий с соответствующим знаком, действует только в том случае, если эти линии не изменяют своего направления (т.е. функции, графиками которых они являются -- возрастающие или убывающие). В случае с параболой у=х это не так - слева от начала координат функция у=х2 убывает, а справа - возрастает, в результате чего наши условия неверно ограничивают закрашенную область.
Для исправления этой ошибки нужно добавить еще одно условие. Например, "х>=0".
Таким образом, правильным ответом в данном случае будет: На Паскале и Бейсике:
Примеры решения заданий ЕГЭ (принадлежность точки заштрихованной области)
Требовалось написать программу, которая вводит с клавиатуры координаты точки на плоскости (х, у - действительные числа) и определяет принадлежность точки заштрихованной области. Программист торопился и написал программу неправильно.
Последовательно выполните следующее:
- 1) Приведите пример таких чисел х, у при которых программа работает неправильно.
- 2) Укажите, как нужно доработать программу, чтобы не было случаев ее неправильной работы. (Это можно сделать несколькими способами, поэтому можно указать любой способ доработки исходной программы).
Как мы только что обсудили, для задания закрашенной/заштрихованной области нужно использовать 4 условия:
х>0, х<=1,5,.у>=0 и y<=x 2 , которые должны выполниться одновременно.
Изучаем предложенную программу и замечаем, что одного условия - х>=0 - не хватает. Без него под систему условий х<=1,5, у>=0 и у<=x 2 подпадают также точки под параболой слева от оси OY и сверху от оси ОХ. Чтобы ответить на первый вопрос задачи (и получить свой первый балл), вычислим какую-нибудь точку из этой области. Она должна быть сверху от оси ОХ (значит, у>0), слева от оси OY (значит, х<0) и ниже параболы (значит, у<=x 2 ). Возьмем какую-нибудь точку на оси ОХ такую, что х<=0, например, х= -1. Для нее должно выполниться y>=0 и у<=х. То есть нас устроит любое значение у от 0 до (-1) 2 . Например, 0,5.
Отвечаем на первый вопрос: х=-1y=0,5
Однако за такое решение мы получим еще только один балл (из двух возможных).
Второй балл нам не дадут, потому что в программе "спрятана" не одна ошибка, а две - во-первых, программа не проверяет условие х<=0; во-вторых, система IF' ов, которая использована в программе, содержит только один ELSE. А он, как известно, относится только к последнему IF'y, у которого нет своего ELSE.
То есть, программа работает неправильно не только для вычисленной нами еще одной области, но и для всех случаев, когда условия первых двух IF'ob не выполняются (при у>х 2 и при х>1.5). В этих случаях программа просто ничего не выдает в качестве ответа (а должна выдавать "не принадлежит").
Либо (что гораздо проще и короче) записать условие принадлежности точки области через сложное условие (через логическое И). Рекомендуемый ответ должен выглядеть так:

- Вопрос задан более трёх лет назад
- 4661 просмотр
Подставляешь X точки в функцию, вычисляешь Y для этой функции.
Сравниваешь с Y точки. Если они равны, точка лежит на линии, если нет, лежит выше или ниже соответственно.
И просто выставляешь необходимые условия проверки, как должна лежать точка, выше или ниже заданных линий.


Круг:
(x - x0)^2+(y-y0)^2 < R^2 - множество точек внутри круга
(x - x0)^2+(y-y0)^2 > R^2 - множество точек вне круга
R - радиус круга, x0, y0 - координаты центра
Эллипс:
((x - x0)/a)^2+((y-y0)/b)^2 < 1 - множество точек внутри эллипса
((x - x0)/a)^2+((y-y0)/b)^2 > 1 - множество точек вне эллипса
a, b - радиусы эллипса
Прямые:
x < 0 - множество точек левее оси 0Y
x > 0 - множество точек правее оси 0Y
y < 0 - множество точек ниже оси 0X
y > 0 - множество точек выше оси 0X
ax+by < c множество точек ниже прямой, заданной уравнением ax+by = с
ax+by > c множество точек выше прямой, заданной уравнением ax+by = с
Для вашей задачи:
1. Находите нужные коэффициенты для всех прямых и кривых.
2. Выясняете для каждого уравнения знак, который получается при попадании точки в заштрихованной области
3. Создаёте набор тестов для точки.
Например для зоны B:
Точка должна быть внутри круга, вне эллипса и выше прямой, то есть должны выполняться следующие неравенства (коэффициенты a, b x0, y0 для каждого неравенства свои):
(x - x0)^2+(y-y0)^2 < R^2
((x - x0)/a)^2+((y-y0)/b)^2 > 1
ax+by > c
Дальше для тестовой точки проверяете неравенства, и если они все правильные - точка принадлежит заштрихованной области.
Хотите улучшить этот вопрос? Обновите вопрос так, чтобы он вписывался в тематику Stack Overflow на русском.
Закрыт 6 лет назад .
Попадает ли точка с заданными координатами в заштрихованную область?

Определить, с какой стороны от прямой находится точка, можно через простое неравенство.
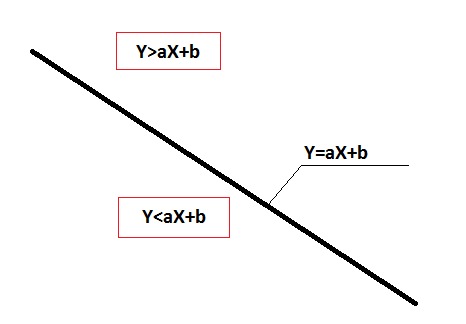
У вас четыре прямые на координатной плоскости:
Проставив нужные знаки неравенства, вы отсечете искомую вами фигуру.
Итоговое решение на С++ записывается в пару строк.

Мне одному непонятно, зачем тут C++11? А на C++03 или, страшно сказать, голом C эта задача уже считается нерешаемой? Я считаю, что преподавание информатики на C++ (заметьте - не преподавание самого C++) - это преступление хуже педофилии. Педофил, по крайней мере, не всем своим ученикам жизнь ломает. Те, кто считает, что информатику надо преподавать на C++ - опасные сумасшедшие. Даже к преподавателям, до сих пор втуляющим детям Turbo Pascal и QBASIC, я отношусь лучше. Они просто безобидные деревенские дурачки.
2,129 10 10 серебряных знаков 15 15 бронзовых знаковВ задачах этого вида дан рисунок координатной плоскости, и некоей закрашенной/заштрихованной области, ограниченной набором прямых и кривых. Нужно определить, принадлежит ли точка с координатами (x,y) этой области или нет.
Так как уравнения всех границ указаны на графике, задачи этого вида требуют понимания того, какой знак нужно поставить в соответствующем неравенстве. плоскость бейсик паскаль программа
Выписав все неравенства, которые "ограничивают" закрашенную/заштрихованную область, и объединив их логической операцией «И» («AND»), получим условие, которое должна проверять программа. Если условие выполняется - точка принадлежит области, если не выполняется - не принадлежит.
Так, если искомую область ограничивает вертикальная прямая линия, то в общем виде уравнение этой прямой выглядит как
где а - то значение на оси х, через которое проходит данная прямая (напомним, что если эта прямая совпадает с осью у, то уравнение прямой будет "х=0").
Так как ось х направлена вправо (на что указывает "стрелка"), то все значения координаты x справа от нашей прямой будут больше числа а. А все значения координаты х слева от нашей прямой ("х=а") будут меньше а. Получаем, что если закрашенная/заштрихованная область лежит справа от прямой "х=а", то все ее точки удовлетворяют условию "х>=а", а если слева - то условию "х<=а".
Замечание относительно нестрогого неравенства (почему нужно писать именно "x>=a v вместо "х>а"): так как на графике все прямые и кривые нарисованы сплошной линией, то закрашенная/заштрихованная область включает свои границы. Поэтому мы и пишем "больше или равно" или "меньше или равно". Строгие неравенства (строго больше/меньше) нужно было бы использовать, если бы границы области были бы нарисованы пунктиром.
Все остальные прямые и кривые, ограничивающие область, уравнения которых сводятся к виду "у=какое-то_выражение" нужно рассматривать с позиции у-координаты (ведь это именно она стоит в левой части уравнения). Так как ось "у" направлена вверх, то все точки, которые лежат выше прямой/кривой, должны удовлетворять условию "у>=это_выражение", а все точки, лежащие ниже нее- условию "у<=это_выражение". Значит, если закрашенная/заштрихованная область лежит выше рассматриваемой прямой/кривой, то все ее точки удовлетворяют условию "у>=это_выражение", а если ниже - то условию " у<=это_выражение".
Напомним, что если нужная вам прямая горизонтальна, то ее уравнение имеет вид
где b - то значение на оси у, через которое проходит эта прямая. И, конечно, если прямая совпадает с осью х, то ее уравнение имеет вид "у=0".
Вывод уравнения прямой, наклонной к оси х выходит за рамки данной книги. На ЕГЭ по информатике вам это умение не понадобится, т.к. это уравнение будет явно указано на графике. А если вам это интересно для общего развития - полистайте учебник алгебры за предыдущие годы.
Единственный и особый случай, который мы хотели бы рассмотреть и напомнить вам - когда закрашенную/заштрихованную область ограничивает окружность. Если ее центр совпадает с началом координат, то уравнение точек на окружности имеет вид
где R - радиус этой окружности.
Как вы, вероятно, понимаете, левая часть этого уравнения (х 2 +у 2 ) задает квадрат расстояния от начала координат до точки плоскости. Для всех точек нашей окружности это расстояние равно ее радиусу R. Именно в этом смысл уравнения окружности. Значит, для всех точек внутри окружности, включая саму окружность, это расстояние будет меньше R. Это можно выразить неравенством
А для всех точек снаружи окружности неравенство будет "x 2 +y 2 >R 2 ". Рассмотрим пример:

В данной задаче закрашенную область ограничивают три прямые линии: горизонтальная (ее уравнение "у=2"), наклонная (ее уравнение "у=х") и вертикальная (она совпадает с осью у, ее уравнение "х=0").
Относительно горизонтальной прямой закрашенная область находится снизу, поэтому знак неравенства должен быть "меньше или равно" - "у<=2".
Относительно наклонной прямой закрашенная область находится сверху, поэтому знак неравенства должен быть "больше или равно" - "у>=х".
Относительно вертикальной прямой закрашенная область находится справа, поэтому знак неравенства должен быть "больше или равно" - "x>=0".
Итого получаем условие:
на Паскале и на Бейсике:
На Бейсике и Си, в данном случае, скобки можно не писать. Но лучше приучиться писать их всегда, чтобы не задумываться каждый раз, нужны они или нет.
В этом примере задача была очень простой - закрашенная область была ограничена только прямыми линиями. Если же область ограничена кривыми (или хотя бы одной кривой), то в список условий обычно приходится добавить еще одно или два условия- ведь кривая может в стороне от закрашенной области изменять свое направление.
И тогда получится, что набора ограничений, который мы написали, просто перечислив линии, ограничивающие область, может оказаться недостаточно. Рассмотрим пример:

Линий, ограничивающих закрашенную область, три: вертикальная прямая х=1,5, горизонтальная прямая у=0 и кривая у=х 2 .
Руководствуясь вышеприведенными рассуждениями, строим систему условий:
х<=1.5 (закрашенная область лежит левее вертикальной прямой), y>=0 (закрашенная область лежит выше горизонтальной прямой) и у<=x 2 (закрашенная область лежит ниже кривой).
Однако, этих условий недостаточно, чтобы ограничить закрашенную область.
Например, чтобы это понять, можно воспользоваться методом "штриховки": для каждого условия заштрихуем разными способами область плоскости, удовлетворяющую этому условию. Там, где все штриховки пересекутся (наложатся одна на другую), все условия будут выполняться.

На рисунке видно, что все три штриховки накладываются друг на друга не только на закрашенной области, но и в области, на которую указывает пунктирная стрелка. Этот эффект объясняется очень просто - правило, которое позволяет задать область плоскости, просто перечислив уравнения ограничивающих линий с соответствующим знаком, действует только в том случае, если эти линии не изменяют своего направления (т.е. функции, графиками которых они являются -- возрастающие или убывающие). В случае с параболой у=х это не так - слева от начала координат функция у=х2 убывает, а справа - возрастает, в результате чего наши условия неверно ограничивают закрашенную область.
Для исправления этой ошибки нужно добавить еще одно условие. Например, "х>=0".
Таким образом, правильным ответом в данном случае будет: На Паскале и Бейсике:
Примеры решения заданий ЕГЭ (принадлежность точки заштрихованной области)
Требовалось написать программу, которая вводит с клавиатуры координаты точки на плоскости (х, у - действительные числа) и определяет принадлежность точки заштрихованной области. Программист торопился и написал программу неправильно.
Последовательно выполните следующее:
- 1) Приведите пример таких чисел х, у при которых программа работает неправильно.
- 2) Укажите, как нужно доработать программу, чтобы не было случаев ее неправильной работы. (Это можно сделать несколькими способами, поэтому можно указать любой способ доработки исходной программы).
Как мы только что обсудили, для задания закрашенной/заштрихованной области нужно использовать 4 условия:
х>0, х<=1,5,.у>=0 и y<=x 2 , которые должны выполниться одновременно.
Изучаем предложенную программу и замечаем, что одного условия - х>=0 - не хватает. Без него под систему условий х<=1,5, у>=0 и у<=x 2 подпадают также точки под параболой слева от оси OY и сверху от оси ОХ. Чтобы ответить на первый вопрос задачи (и получить свой первый балл), вычислим какую-нибудь точку из этой области. Она должна быть сверху от оси ОХ (значит, у>0), слева от оси OY (значит, х<0) и ниже параболы (значит, у<=x 2 ). Возьмем какую-нибудь точку на оси ОХ такую, что х<=0, например, х= -1. Для нее должно выполниться y>=0 и у<=х. То есть нас устроит любое значение у от 0 до (-1) 2 . Например, 0,5.
Отвечаем на первый вопрос: х=-1y=0,5
Однако за такое решение мы получим еще только один балл (из двух возможных).
Второй балл нам не дадут, потому что в программе "спрятана" не одна ошибка, а две - во-первых, программа не проверяет условие х<=0; во-вторых, система IF' ов, которая использована в программе, содержит только один ELSE. А он, как известно, относится только к последнему IF'y, у которого нет своего ELSE.
То есть, программа работает неправильно не только для вычисленной нами еще одной области, но и для всех случаев, когда условия первых двух IF'ob не выполняются (при у>х 2 и при х>1.5). В этих случаях программа просто ничего не выдает в качестве ответа (а должна выдавать "не принадлежит").
Либо (что гораздо проще и короче) записать условие принадлежности точки области через сложное условие (через логическое И). Рекомендуемый ответ должен выглядеть так:
Читайте также:


