Методы решения систем линейных уравнений в приложении microsoft excel презентация
Презентация на тему: " РЕШЕНИЕ УРАВНЕНИЙ В СРЕДЕ MS EXCEL. Решение линейных уравнений уравнений с помощью средства «Подбор параметра» Пример 1 Найти все корни уравнения 3cos2x-sinx." — Транскрипт:
1 РЕШЕНИЕ УРАВНЕНИЙ В СРЕДЕ MS EXCEL
2 Решение линейных уравнений уравнений с помощью средства «Подбор параметра» Пример 1 Найти все корни уравнения 3cos2x-sinx = 0 при x [0;3]
3 Шаг 1 Табулируем функцию 3cos2x-sinx = 0 с шагом 0,3 на отрезке [0;3] . При решении уравнений с помощью средства Подбор параметра значения переменной должны быть заданы числом
4 Из таблицы значений видно, что функция на [0;3] меняет знак два раза: при х [0,6;0,9] и х [2,4;2,7], на этих отрезках есть точки пересечения функции с осью Х
5 Найдем корни полинома методом последовательных приближений с помощью средства поиск решения: Сервис > Подбор параметра
6 Скопируйте формулу из ячейки В2 в F2 (теперь формула ссылается на пустую ячейку Е2, поэтому в F2 отражается 0) Установите в ячейку Е2 значение переменной из [0,6;0,9], например х=0,7
7 Зададим относительную погрешность вычислений 0,00001 и предельное число итераций 1000 Сервис > Параметры > Вычисления
9 В качестве начальных значений приближений к корням можно взять любые точки из отрезков локализации корней, например 0,7 и 2,5
10 Установите курсорную рамку в ячейку F2 и выполните Сервис, Подбор параметра Аналогично найдите второй корень уравнения
11 РЕШЕНИЕ СИСТЕМЫ НЕЛИНЕЙНЫХ УРАВНЕНИЙ В СРЕДЕ MS EXCEL С ИСПОЛЬЗОВАНИЕМ СРЕДСТВА «ПОИСК РЕШЕНИЯ»
12 Пара (х;у) является решением системы уравнений тогда и только тогда, когда она является решением следующего уравнения с двумя неизвестными: (х 2 +у 2 -3) 2 +(2х+3у-1) 2 =0
13 Решением системы - точки пересечения окружности r=3 и прямой уравнение имеет не более двух различных решений Определяемое значение нелинейной задачи зависит от начального приближения
14 Для локализации корней протабулируем левую часть уравнения (х 2 +у 2 -3) 2 + (2х+3у-1) 2 = 0 по переменным х и у на [-3;3] шагом 1,5
15 Протабулируем функцию с помощью таблицы подстановки F(x;y)=(х 2 +у 2 -3) 2 +(2х+3у-1) 2
16 Из таблицы видно, что начальное приближение к корню следует выбрать следующие пары значений (-1,5;1,5), (1,5;0) и (1,5;1,5)
17 Для нахождения корней уравнения введем соответствующие пары значений (х; у) для первого корня в ячейки в А10, А11 для второго корня в ячейки в А14,А15 для третьего корня в ячейки в А17,А18 F(x;y) соответственно в ячейки В13, В16, В19
18 Найдем первый корень. 1.Установить курсорную рамку в ячейке В15 2.Выполнить Сервис > Поиск Решения
21 После нажатия кнопки Выполнить средство Поиск решения находит решение, которое помещает в ячейки А11, А12 Аналогично находим второй и третий корни. Решением уравнения будут две пары значений (-1,269;1,179) (1,576;-0,717)
22 РЕШЕНИЕ МАТРИЧНЫХ УРАВНЕНИЙ
23 Простейшие операции над массивами МАССИВ - объект Excel, используемый для получения нескольких значений в результате вычисления одной формулы или для работы с набором аргументов, расположенных в различных ячейках и сгруппированных по строкам или столбцам.
24 Два типа массивов Microsoft Excel : диапазон массива - непрерывный диапазон ячеек, использующих общую формулу; диапазон констант - набор констант, используемых в качестве аргументов функций.
25 диапазон констант - набор констант, используемых в качестве аргументов функций диапазон массива - непрерывный диапазон ячеек, использующих общую формулу;
27 Для умножения (деления) массива на число: 1.Выделить диапазон ячеек того же размера 2.Ввести в первую ячейку диапазона формулу =Е1:G3*100 и нажать комбинацию клавиш SHIFT+ CTRL+ENTER Если в формуле используется ссылка на ячейку в которой хранится число, то ссылка на эту ячейку должна быть абсолютной
28 Формула массива обрабатывает несколько наборов значений (аргументов массива). Каждый аргумент массива должен включать одинаковое число строк и столбцов. Формула массива создается так же, как и другие формулы, только что для ввода такой формулы используются комбинация клавиш SHIFT+ CTRL+ENTER
29 Пример Перемножение массивов: 1.Выделить область такого же размера как перемножаемые массивы 2.Ввести в первую ячейку формулу =А1:С3*А1:С7 3.Для ввода массива нажать комбинацию SHIFT+ CTRL+ENTER Сложение, вычитание, деление, вычисление каждого элемента как результата некоторой функции производится аналогично. При вводе формулы массива Microsoft Excel автоматически заключает ее в фигурные скобки
30 Формула массива может выполнить несколько вычислений, а затем вернуть одно значение или группу значений. Пример Рассчитать суммарный балл оценки экспертом качества услуги по формуле: Si - суммарный балл Wi – вес критерия Ci – оценка критерия экспертом N – количество критериев
31 Способ решения 1 1.Введите в ячейку D2 формулу =В2*С2 и скопируйте ее в ячейки диапазона D3:D7 2.Введите в ячейку D8 формулу = СУММ(D2:D7) 3.В ячейке D9 вычислите значение S = D86
33 Функцию можно ввести в ячейку с клавиатуры или с помощью средства Мастер функций Каждая функция выводится в стандартном окне диалога Для ввода аргумента достаточно указать в соответствующих полях числовые значения аргументов, адреса ячеек или адреса диапазонов ячеек
35 Окно диалога функции Суммпроизв() Результат вычисления формулы - число
36 Функции для работы с массивами МУМНОЖ(массив1;массив2) - перемножает массивы. Массивы (матрицы) должны быть одной размерности и оба массива должны содержать только числа.
37 МОБР(массив)- возвращает обратную матрицу для матрицы, хранящейся в массиве
38 ТРАНСП(массив) - используется для того, чтобы поменять ориентацию массива на рабочем листе с вертикальной на горизонтальную и наоборот.
39 МОПРЕД(массив) - возвращает определитель матрицы (матрица хранится в массиве). Определитель матрицы - это число, вычисляемое на основе значений элементов массива. Для массива A1:C3, состоящего из трех сток и тех столбцов, определитель вычисляется следующим образом: = A1*(B2*C3-B3*C2) + A2*(B3*C1-B1*C3) + A3*(B1*C2-B2*C1)
40 СУММСУММКВ(массив_x;массив_y) - возвращает сумму сумм квадратов соответствующих элементов двух массивов. Сумма сумм квадратов - это распространенный термин во многих статистических вычислениях. Массив_x - это первый массив или интервал значений. Массив_y - это второй массив или интервал значений.
41 СРГЕОМ(число1;число2;. ) - возвращает среднее геометрическое значений массива или интервала положительных чисел. Например, функцию СРГЕОМ можно использовать для вычисления средних темпов роста, если задан составной доход с переменными ставками. СУММКВРАЗН(массив_x;массив_y) - возвращает сумму квадратов разностей с оответствующих значений в двух массивах. Массив_x - это первый массив или интервал значений. Массив_y - это второй массив или интервал значений.
42 ЧИСЛСТОЛБ(массив) - возвращает количество столбцов в ссылке или массиве: =ЧИСЛСТОЛБ(A1:D9) в ячейке отображается число 4 ЧСТРОК(массив) - возвращает количество строк в ссылке или массиве. = ЧСТРОК (A1:D9) в ячейке отображается число 9 Статистические функции, который используются для прогнозирования Тенденция(), Рост(), Предсказ(), Линейн() также используют правило ввода значений массива
43 Решение матричных уравнений в EXCEL Найти решение уравнения А*Х=В А-матрица коэффициентов В- столбец (вектор) свободных членов Х-столбец (вектор)неизвестных Решение линейной системы имеет вид: Х=А -1 *В А -1 – обратная матрица
44 Шаг 1. Вычислим А -1 с помощью функции =МОБР(массив) Шаг 2. Выделить диапазон К2:К4 для элементов массива вектора Х и ввести формулу =МУМНОЖ(E2:G4;I2:I4) Для вставки массива нажать комбинацию клавиш SHIFT+ CTRL+ENTER
45 Шаг 3. Проверка. Умножим матрицу А на найденный вектор Х В результате мы должны получить вектор В Выделим диапазон М2:М4 и введем функцию = МУМНОЖ(А2:С4;К2:К4) Для вставки массива нажать комбинацию клавиш SHIFT+ CTRL+ENTER
46 Самостоятельно решить системы линейных уравнений А 2 *Х=В и А 3 *Х=В
47 Решить уравнение Z=Х т A X А-матрица, Х-вектор, Х T - транспонированный вектор Шаг1. Найти транспонированный вектор Х T Выделать диапазон G2:I2 и ввести формул =ТРАНСП(E2:E4) для ввода массива значений нажать SHIFT+ CTRL+ENTER
48 Шаг2. Умножить полученную строку Х T на матрицу Авыделить диапазон К2:М2 и ввести формулу =МУМНОЖ(G2:I2;A2:C4) Шаг 3. В отдельную ячейку введите формулу =МУМНОЖ(K2:M2;E2:E4) – результат вычисления число 227, но для ввода нажать SHIFT+ CTRL+ENTER
49 Это же решение можно получить путем ввода в ячейку одной формулы, содержащей вложенные функции: =МУМНОЖ(МУМНОЖ(ТРАНСП(E2:E4);A2:C4);E2:E4) Самостоятельно решить уравнения: 1. Z=Y т A т AY 2. Z=Y т A т A 2 Y
50 Решение системы линейных уравнений методом Гаусса
51 1. Ввести матрицу коэффициентов в ячейки рабочего листа MS Excel 2. Скопировать первую строчку (диапазон А1:Е6) в диапазоны А6:Е6 А11:Е11 А16:Е16
53 3. Выделить диапазон А7:Е7 и введите формулу, которая обращает в 0 коэффициент при х 1 во втором уравнении системы: =A2:E2-$A$1:$E$1*(A2/$A$1) Для вставки элементов массива нажать SHIFT+ CTRL+ENTER Выделить диапазон А7:Е7 и протащить маркер автозаполнения этого диапазона, чтобы заполнить диапазоны А7:Е7 в диапазон А8:Е8 и А9:Е9. Это обратит в 0 коэффициенты при х 1 в третьем и четвертом уравнениях системы.
54 4. Выделить диапазон А7:Е7 и скопируйте значения в буфер Выделите диапазон А12:Е12 и выполните вставку значений без формул используйте команду Правка, специальная вставка Аналогично вставьте значения в диапазон А17:Е17
56 5. Выделите диапазон А19:Е19 и введите формулу массива, которая обращает в 0 коэффициент при х 3 =A14:E14-$A$13:$E$13*(C14/$C$13) Для вставки элементов массива нажать SHIFT+ СTRL+ENTER Прямая прогонка метода Гаусса завершена

Помогите другим пользователям — будьте первым, кто поделится своим мнением об этой презентации.
Аннотация к презентации
Посмотреть презентацию на тему "Решение систем уравнения в EXСEL" для 11 класса в режиме онлайн с анимацией. Содержит 11 слайдов. Самый большой каталог качественных презентаций по информатике в рунете. Если не понравится материал, просто поставьте плохую оценку.
Содержание

Решение системы уравнений в Excel методом Крамера и обратной матрицы

Метод Крамера
Ме́тодКра́мера — способ решения систем линейных алгебраических уравнений с числом уравнений равным числу неизвестных с ненулевым главным определителем матрицы коэффициентов системы (причём для таких уравнений решение существует и единственно). Для системы n линейных уравнений с n неизвестными - основная матрица системы.

Определитель квадратной матрицы равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения - определитель системы: Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Нахождения неизвестных переменных по методу Крамера
а11X1+a12X2=B1 a21X1+a22X2=b2 X1=

Метод обратной матрицы
Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит следующем . Пусть дана система линейных уравнений с неизвестными (над произвольным полем): Тогда её можно переписать в матричной форме: А*X=B,где А- основная матрица системы;B и X - столбцы свободных членов и решений системы соответственно:

Найдём обратную матрицу по формуле: Таким образом, решение системы линейных алгебраических уравнений матричным методом определяется по формуле

Вычислить значения корней сформированной системы уравнений двумя методами: обратной матрицы и методом Крамера.

Решение СЛАУ методом Крамера в Excel
Находим матричный определитель: Находим определители Xn, заменяя каждый столбец матрицей B

Определители Xn порядка делим на матричный определитель и получаем ответ

Решение СЛАУ методом обратной матрицы
Мышкой выделить квадратную область клеток, где будет размещена обратная матрица. 2. Начать вписывать формулу =МОБР 3. Выделить мышкой матрицу А. При этом правее скобки впишется соответству- ющий диапазон клеток. 4. Закрыть скобку, нажать комбинацию клавиш: Ctrl-Shift-Enter 5. Должна вычислиться обратная матрица и заполнить предназначенную для неё область

1.Начать вписывать формулу =МУМНОЖ 2.Выделить мышкой матрицу - первый сомножитель. 3. Выделить мышкой вектор- второй сомножитель. 4.нажать комбинацию клавиш: Ctrl-Shift-Enter5. Вычислиться произведение и заполниться предназначенная для неё область.
Загрузить презентацию (764 кБ)
Тема “Решение математических задач средствами EXCEL”, является значимой в курсе “Информатика и информационные технологии”, которая возникает на различных этапах изучения предмета. Например, вычисления алгебраических выражений, решения квадратных уравнений в различных средах, построение графиков функций и т.д.
На протяжении почти всего курса математики учащиеся изучают различные методы решения уравнений и систем уравнений. Когда школьники изучат методы решения систем уравнений на уроках алгебры, на уроках информатики целесообразно рассмотреть дополнительные, более эффективные, по времени, инструменты для выполнения таких заданий. Данная тема не является сложной для учащихся, но очень трудоемкая для учителя, необходимо делать много записей на доске, фактически учитель весь урок стоит спиной к учащимся. Для оптимизации и эффективности учебной деятельности учителя на уроке была создана презентация, которая может применяться на любом этапе прохождения темы фрагментарно или полностью учителями математики, а особенно полезна учителям информатики из-за ограниченного количества часов по предмету.
Данный урок можно отнести к интегрированным урокам, построенным на деятельной основе с применением проблемно-исследовательской технологии. Ценность урока заключается в том, что ученики решают стандартные математические задачи нестандартным способом – применяя современные компьютерные технологии. Этим достигается мотивационная цель – побуждение интереса, показ необходимости знаний по математике и информатики в реальной жизни. На уроке ученики покажут владение компьютером, умение работать с пакетом программ Microsoft Office, знания, умения и навыки, полученные на уроках математики. В результате будет достигнута образовательная цель урока: по математики обобщение знаний по темам: “Матрицы. Действия с матрицами. Решение систем линейных уравнений методом Крамера, Гаусса”, по информатике у учащихся формируется навык работы с табличными формулами, познакомятся с возможностями Excel для решения различных уравнений и систем уравнений.
11 класс, информатика.
Тема: “Применение табличного процессора MS Excel для решения систем линейных алгебраических уравнений”.
Тема рассчитана на два урока.
Тип урока: комбинированный урок, совершенствование знаний, умений и навыков.
Вид урока: интегрированный.
-
повторение и закрепление знаний учащихся математического аппарата по теме;
- отработать умение переходить от математической записи выражений к записи в среде электронных таблиц;
- продемонстрировать учащимся рациональность использования электронных таблиц для решения систем п линейных уравнений с п неизвестными;
Развитие внимания, памяти, представления, мышления, речи. Развитие интереса к предмету, навыка самостоятельной работы.
-
формирование умений анализировать, выделять главное, сравнивать, строить аналогии;
- развитие умения применять имеющиеся знания и умения в новой ситуации;
- развивать гибкость мышления, отыскивать наиболее краткий путь достижения цели развивать целенаправленность, рациональность, критичность мышления.
- умение устанавливать межпредметные связи.
- формирование способностей, позволяющих осуществлять быструю смену видов учебной деятельности.
Формы организации познавательной деятельности: фронтальная, индивидуальная, групповая, коллективная.
Методы и приемы обучения: объяснительно-иллюстративный, проблемного изложения, наглядно-иллюстративный, практический, эвристическая беседа.
Оборудование: доска, компьютеры, мультимедийный проектор и экран, презентация, карточки с индивидуальным заданием, папка с электронным материалом для урока.
Средства обучения: презентация учителя MS PowerPoint “Решение математических задач средствами Excel”, ресурсы Интернет.
Компьютерное программное обеспечение: пакет программ Microsoft Office 2007.
- Учитель сообщает учащимся тему и цель урока. Учащиеся записывают тему урока Слайд Титульный лист.
- Рассказывает о том, как будет построен урок.
- Знакомит с задачами, которые должны быть решены в ходе урока.
2. Актуализация опорных знаний.
Учитель. Для успешного проведения занятия по теме нам необходимо будет вспомнить и повторить материал из уроков математики “Методы решения линейных систем уравнений” и из информатики “Работа с формулами в Excel. Логические формулы. Относительные и абсолютные ссылки”.
Откройте файл D://Уроки_11/Решение СЛАУ/Приложение 2. У учащихся файл без листа Решение.
Заполните все поля таблицы.
Фронтальная работа с учащимися по проверки знаний и умений работы с формулами и функциями в Excel. На экране демонстрируется пример таблицы,

в которой необходимо заполнить все поля. Учащиеся предлагают алгоритмы заполнения полей. В тетради выписывают формулу для заполнения столбца K (победители, призеры), далее сравнивают свое решение с решением, представленным на экране (лист Решение, Приложение 2).

3. Изучение нового материала.
Какие методы решения линейных уравнений вы знаете? Если не просмотрели файл выложенный в домашнее задание предыдущего урока, то можете открыть файл D://Уроки_11/Решение СЛАУ/Приложение 1.
Метод последовательного исключения неизвестных, метод Крамера.
Посмотрите описание метода Крамера, с какими элементами нужно уметь работать при применении этого метода?
Т.е. с матрицами, на экране демонстрируется пример матрицы . Откройте файл D://Уроки_11/Решение СЛАУ/Приложение 3, лист Пример и выполните задание.
Учащиеся открывают документ Приложение 3 (лист Пример 1).
Выполняются задания, представленные на экране.
Для работы с матрицами в Excel существуют специальные формулы, формулы для работы с массивом или их ещё называют табличные формулы.
Презентация. Слайд 3, 4. Учащиеся записывают понятие табличной формулы и особенности её ввода.
4. Подготовка к осмысление и применение изученного материала. Практическая работа.
1. Для решения, каких задач можно применять табличные формулы?
Ответ может быть предопределен заданием, которое они выполняли – действия с матрицами, если решением должна получиться тоже матрица.
2. Дайте понятие матрицы? Может ли сказать, что любая прямоугольная таблица, заполненная числовыми значениями, есть матрица?
Ответ утвердительный. Слайд 5
3. Какие виды матриц вы знаете, чем они отличаются друг от друга? (заполнение, размерность и т.д.)
После обсуждения представить Слайд 6.
4. Можно ли с матрицами производить какие-либо действия?
Учащиеся могу перечислить некоторые действия с матрицами, сложение, умножение на число и т.д. Слайд 7.
Учитель информирует учащихся , о широких возможностях табличного процессора Excel для работы с матрицами.
Ученики записывают тему пункта темы Слайд8.
Повторение, обобщение математических знаний, дополненных демонстрацией новых функций Excel.
Презентация Слайды 9-14.
Демонстрация каждого слайда предопределяется вопросами по теме слайда.
В тетрадь учащиеся записывают только функции Excel для работы с матрицами и одновременно выполняют тренировочные практические задания из Приложение 3 Листы: пример 2, пример 3, пример 4. Подробно остановиться на примере 5, Приложение 3, Слайд 14.
Теперь непосредственно перейдем к решению СЛАУ и познакомимся с методом, который вы рассматривали на уроках математики, это матричный метод. Слайд 16. Как вы думаете почему вы не решали системы матричным методом?
Сложность вычисления обратной матрицы
Запишите в тетрадь алгоритм решения системы матричным способом.
Учитель открывает файл – заготовку упражнения и вместе с учащимися решает упражнение.
Рассмотрим теперь решение СЛАУ методом Крамера, этот метод вам знаком, но на уроках математики вы решали, в основном, системы из двух уравнений с двумя неизвестными, почему? Слайд 22.
Нужно много времени для вычисления определителей.
Возможности Excel решают эту проблему. Откройте новый лист в книге и вместе решим систему уравнений представленную на экране.
Свои решения учащиеся сравнивают с решением, представленным в презентации. Слайды 23-25.
5. Закрепление (эвристическая беседа, тренировка, отработка умений).
Проверка практической работы, обсудить проблемы в выполнении с каждой группой, если были выполнены не все задания, то откорректировать домашнее задание. Выставление оценок за урок.
Домашнее задание. На выбор:
1. (Приложение 4) Выполнить один из вариантов из карточки , разобрать программы решения систем уравнений на языке Паскаль из теоретического материала (Приложение 1)
2. Выполнить один из вариантов из карточки. Создать отдельно программу для решения систем методом Гаусса или матричным методом, группе программистов доработать программу метод Крамера.
Опыт работы с интегрированными уроками показывает, что у учащихся повышается качество знаний, оно может и не выражаться в оценках, но расширяется кругозор, развиваются творческие способности, повышается интерес к предметам, и вообще интерес к обучению, формируется убеждение, что учащиеся могут изучить больше, чем дается по программе.
Предложенное занятие по содержанию и выполнению заданий, кажется, насыщенным и перегруженным теорией и практическими упражнениями, но применение презентации, заготовок файлов (приложение 3) помогает выполнить все запланированные действия. Такое занятие рекомендуется проводить в математических классах, когда учащиеся уже изучили методы решения СЛАУ. За неделю до изучения этой темы выложить в эл. дневник, для ознакомления, информационный материал по методам решения систем уравнений и описание создания программ для решения систем уравнений на языке программирования.
1. Воронина Т.П. Образование в эпоху новых информационных технологий / Т.П. Воронина.- М.: АМО, 2008. -147 с.
2. Глинская Е. А. Межпредметные связи в обучении / Е.А. Глинская, С.В. Титова. – 3-е изд. – Тула: Инфо, 2007. - 44 с.
3. Данилюк Д. Я. Учебный предмет как интегрированная система /Д.Я. Данилюк //Педагогика. - 2007. - № 4. - С. 24-28.
4. Иванова М.А. Межпредметные связи на уроках информатики / М.А. Иванова, И.Л. Карева // Информатика и образование. – 2005. - №5. – С. 17-20.
5. А.В. Могилев, Н.И. Пак, Е.К. Хеннер "Информатика", Москва, ACADEMA, 2000 г.

Решение системы уравнений в Excel методом Крамера и обратной матрицы

Метод Крамера Ме тод Кра мера — способ решения систем линейных алгебраических уравнений с числом уравнений равным числу неизвестных с ненулевым главным определителем матрицы коэффициентов системы (причём для таких уравнений решение существует и единственно). Для системы n линейных уравнений с n неизвестными - основная матрица системы.

Определитель квадратной матрицы равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения - определитель системы: Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Нахождения неизвестных переменных по методу Крамера

Метод обратной матрицы Ма тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит следующем . Пусть дана система линейных уравнений с неизвестными (над произвольным полем): Тогда её можно переписать в матричной форме: А*X=B, где А- основная матрица системы; B и X - столбцы свободных членов и решений системы соответственно:

Найдём обратную матрицу по формуле: Таким образом, решение системы линейных алгебраических уравнений матричным методом определяется по формуле

Вычислить значения корней сформированной системы уравнений двумя методами: обратной матрицы и методом Крамера.

Решение СЛАУ методом Крамера в Excel

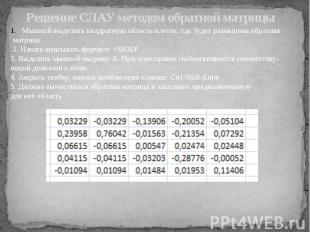
Решение СЛАУ методом обратной матрицы

1.Начать вписывать формулу =МУМНОЖ 2.Выделить мышкой матрицу - первый сомножитель. 3. Выделить мышкой вектор- второй сомножитель. 4.нажать комбинацию клавиш: Ctrl-Shift-Enter 5. Вычислиться произведение и заполниться предназначенная для неё область.
Читайте также:


