Расчет усилия гибки листового металла
Величина внешнего изгибающего момента при гибке определяется из условия равновесия его с моментом внутренних сил, а последний слагается из моментов нормальных напряжений в растягиваемой и сжимаемой зонах.
Для определения моментов внутренних сил необходимо знать распределение напряжений по поперечному сечению и величину наибольшего напряжения для данной степени деформации.
Усилие гибки определяется из равенства внешнего изгибающего момента моменту внутренних сил. Изгибающие моменты для различных схем гибки следующие: для одноугловой:
В табл. 23 приведены формулы усилия гибки для свободного изгиба, для гибки с прижимом и приближенные формулы для гибки с калибровкой материала. В последнем случае усилие гибки определяется не столько процессом изгиба, сколько процессом калибровки, требующим значительного давления и практически зависящим от регулировки хода пресса и от отклонений материала по толщине.
Таблица 23. Формулы для определения усилий гибки
Обозначения: РК - усилие калибровки, кгс;
РПР - усилие прижима, кгс, составляющее (0,25/0,3) РИЗ;
В - ширина полосы (длина линии изгиба), мм;
l - расстояние между опорами при угловой гибке, мм;
n = 1,8 - коэффициент, характеризующий влияние упрочнения;
р - давление калибровки (правки), кгс/мм 2 (по табл. 24);
F - площадь калибруемой заготовки (под пуансоном), мм 2 ;
k1 - коэффициент для свободной гибки, находимый по табл. 24;
k2 - коэффициент для двухугловой гибки, приведенный в табл. 25.
Оптимальным плечом для свободного изгиба следует считать:
, где I - расстояние между опорами, мм.
Усилие, необходимое для двухугловой гибки, больше усилия одноугловой гибки заготовки тех же размеров. В данном случае изгиб осуществляется действием двух изгибающих моментов, что при прочих равных условиях требует удвоенного усилии.
Но и одностороннее усилие при двухугловой гибке больше усилия одноугловой (V-образной) гибки потому, что при одном и том же изгибающем моменте, плечо двухугловой гибки меньше. Кроме того к усилию двухугловой гибки необходимо прибавить усилие прижима, составляющее 0,25-0,3 усилия изгиба. В некоторых случаях целесообразно применять усилие прижима большей величины (0,5 / 0,6) РИЗ.
На рис. 69 приведены схемы двухугловой гибки (левой полки). На рис. 69,а показано начальное положение и эпюра одностороннего изгибающего момента (для. точек А, В, С), а на рис. 69,б - дальнейшая стадия изгиба со схемой сил, действующих на заготовку.
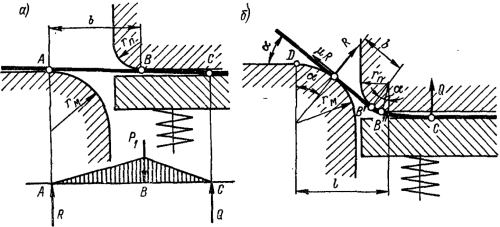
Рис. 69. Схема двухугловой гибки
Установлено, что в зависимости от геометрических соотношений максимальное усилие двухуглового изгиба возникает при величине угла α от 45 до 80°, когда плечо изгиба I имеет наименьшую величину.
В результате исследования [42] установлена более точная величина усилия двухугловой гибки (без усилия прижима):
, где n - коэффициент увеличения номинального зазора (см. табл. 27);
k2 - коэффициент, наибольшее значение которого приведено в табл. 25.
В табл. 23 приведена формула для определения усилия при двухугловой гибке с прижимом. Экспериментальное значение коэффициентов для сталей 08, 10, 20кп, СтЗ, 1Х18Н9Т толщиной 4; 6 и 8 мм в зависимости от rM/S и rП/S приведено в табл. 25.
При несимметричной и криволинейной форме изгиба применяют одноугловую (одностороннюю) гибку с прижимом, так как простая угловая гибка не обеспечивает точности из-за смещения заготовки. Этот случай приближенно можно рассматривать как половину двухугловой гибки с прижимом. Соответствующее усилие гибки приведено в табл. 23. Значения коэффициентов k 2 при прямолинейном изгибе те же.
Односторонняя гибка с прижимом применяется также в комбинированных процессах штамповки.
В табл. 24 приведены значения коэффициента k1 для свободного изгиба, а в табл. 25 k2 - значения для двухуглового изгиба. В табл. 26 даны приближенные значения давления правки (калибровки).
Вальцовка листового металла
В одной из статей блога два с половиной года назад была затронута тема расчета геометрии деталей, получающихся в процессе вальцовки. В этой публикации речь пойдет об определении усилий, возникающих при вальцовке листового металла. Тема интересная.
. и важная не только для специалистов эксплуатирующих листогибочные вальцы, но и для всех, кто, так или иначе, связан с процессом гибки на листогибочных и обычных прессах.
Во всех расчетных формулах для определения усилия гибки листов в качестве одних из главных определяющих параметров фигурируют или предел прочности, или предел текучести металла листовой заготовки. Известно, что в процессе изгиба область, подверженная деформации, упрочняется. Но на сколько? Иногда это упрочнение учитывают повышающим предел текучести постоянным коэффициентом, как, например, в статье о V-образной гибке. В программе, представленной в этой статье, повышение прочности будет определено и учтено аналитически по расчетной кривой деформационного упрочнения.
В паспортах листогибочных валковых машин в последнее время обычно указывается максимальная ширина и толщина изгибаемой листовой заготовки из стали С255 и наименьший радиус вальцовки. А на практике постоянно возникает вопрос – «потянут» ли вальцы менее широкий, но более толстый лист, да еще, возможно, и из другой марки стали? Вопрос не праздный – ошибка может привести к поломке станка и дорогостоящему последующему ремонту.
Включаем MS Excel и начинаем рассмотрение решения озвученной задачи на примере вальцовки листового металла на трехвалковой листогибочной машине.
Расчет в Excel моментов и сил при вальцовке.
Задача:
Определить возможность гибки и правки обечайки диаметром 1600 мм и длиной 1500 мм из листовой стали С345 (09Г2С) толщиной 18 мм на вальцах марки И2222.
Из паспортных данных машины известно, что на ней можно изготовить обечайку минимальным диаметром 440 мм и длиной 2000 мм из листовой стали С255 (Ст3 сп5) толщиной 16 мм.
Вальцовка листового металла на трехвалковой машине с подвижным в вертикальной плоскости верхним валком показана на схеме, из которой очевидно, что наиболее нагруженным является верхний валок.

Задачу решим следующим образом:
1. Определим в расчете №1 усилие на верхнем валке при гибке и правке обечайки с предельными размерами из паспорта. То есть узнаем возможности листогибочной машины И2222.
2. В расчете №2 вычислим силы, действующие на наиболее нагруженный верхний валок при гибке и правке интересующей нас короткой трубы из стали С345.
3. Сравним значения сил и сделаем выводы.
Расчет №1:

Расчет №2:

Вывод:
Так как усилия на верхнем валке в расчете №2 немного меньше усилий из расчета в Excel №1, то следует вывод: на вальцах И2222 можно изготовить трубу из стали 09Г2С диаметром 1600 мм, длиной 1500 мм с толщиной стенки 18 мм.
Формулы, использованные в расчете:
12. ε т = [σт] / E +0,002
13. m =lg( [σв] / [σт] )/lg( εв / εт )
14. A = [ σв ] /(g* εв m )= [ σт ] /(g* εт m )
15. n = A *2 (2,59- m ) /( E /g *(2+ m ))
16. R о = R + s /2
17. r о = Rо / s
18. R г = Rо /(1+ n * r о (1- m ) )
19. M г =( A * b * s (2+ m ) )/(2 ( m +1) *(2+ m )* Rг m )* g
20. α г =arcsin (( L /2)/( Rг + D /2+ s /2))
21. P г =2* M г /( R г *tg ( αг ))
22. R пр = k ф * Rг
23. M пр =( A * b * s (2+ m ) )/(2 ( m +1) *(2+ m )* Rпр m )* g
24. α пр =arcsin (( L /2)/( Rпр + D /2+ s /2))
25. P пр =2* π * M пр /( R пр *((π- αпр )*tg ( αпр )+1-1/cos ( α пр )))
Заключение.
Расчет в Excel был выполнен без учета веса верхнего валка. Если учесть этот момент, возможности листогибочной машины увеличатся на 2…3%.
Механические свойства сталей в пунктах 4…7 расчета можно найти в ГОСТ 27772-88 ( εт =δ5).
При правке заваренных обечаек изгибающий момент и усилие на верхнем валке возрастают из-за неправильной геометрии подогнутых краев заготовки и усиления сопротивления замкнутого контура.
Коэффициент формы обечайки kф в пункте 11 можно определить по подсказке в примечании к ячейке D13.
Этот коэффициент зависит от способа подгибки краев заготовки:
kф =0,75…0,85 – при вальцовке без подкладного листа с плоскими краями;
kф =0,80…0,90 — при вальцовке без подкладного листа по радиусу;
kф =0,85…0,95 — при вальцовке с подкладным листом:
kф =0,95…1,00 – при гибке на прессе в штампе.
В завершении статьи определим коэффициент упрочнения, о котором упоминалось в самом начале, для каждого из рассчитанных выше вариантов.
K1 = Mг1 /( Wx1 * [σт]1 )=37783899/(2000*16 2 /6*245)=1,81
K2 = Mг2 /( Wx2 * [σт]2 )=42658644/(1500*18 2 /6*325)=1,62
С уменьшением радиуса гибки листа логично нарастает упрочнение. Используя параметры кривой деформационного упрочнения, можно более точно определять усилия и при V-образной гибке на листогибочных прессах.
Смею предположить, что при использовании предложенной программы вальцовка листового металла станет для вас более понятной и безопасной.
Прошу уважающих труд автора скачивать файл с расчетной программой после подписки на анонсы статей в окне, расположенном в конце каждой статьи или в окне вверху страницы!
Гибка металла на вальцах
За последнее время ко мне было несколько обращений от читателей блога за помощью в решении одной и той же задачи: как при работе на трехвалковых листогибочных вальцах и профилегибах определить окончательное местоположение среднего ролика (валка).
. относительно положения крайних роликов (валков), которое обеспечит гибку (вальцовку) заготовки с определенным заданным необходимым радиусом? Ответ на этот вопрос позволит повысить производительность труда при гибке металла за счет уменьшения количества прогонов заготовки до момента получения годной детали.
В этой статье вы найдете теоретическое решение поставленной задачи. Сразу оговорюсь – на практике я этот расчет не применял и, соответственно, не проверял результативность предлагаемого метода. Однако я уверен, что в определенных случаях гибка металла может быть выполнена гораздо быстрее при использовании этой методики, чем обычно.
Чаще всего в обычной практике окончательное местоположение подвижного центрального ролика (валка) и количество проходов до получения годной детали определяется «методом тыка». После длительной (или не очень) отработки технологического процесса на пробной детали определяют координату положения центрального ролика (валка), которую и используют при дальнейших перенастройках вальцев, изготавливая партию этих деталей.
Метод удобен, прост и хорош при значительном количестве одинаковых деталей – то есть при серийном производстве. При единичном или «очень мелкосерийном» производстве, когда необходимо гнуть разные профили или листы разной толщины разными радиусами, потери времени на настройку «методом тыка» становятся катастрофически огромными. Особенно эти потери заметны при гибке длинных (8…11м) заготовок! Пока сделаешь проход…, пока проведешь замеры…, пока перестроишь положение ролика (валка)… — и все сначала! И так десяток раз.
Расчет в Excel местоположения подвижного среднего ролика.
Запускаем программу MS Excel или программу OOo Calc, и начинаем работу!
С общими правилами форматирования электронных таблиц, которые применяются в статьях блога, можно ознакомиться здесь .
Прежде всего, хочу заметить, что листогибочные вальцы и профилегибы разных моделей могут иметь подвижные крайние ролики (валки), а могут — подвижный средний ролик (валок). Однако для нашей задачи это не имеет принципиального значения.
На рисунке, расположенном ниже изображена расчетная схема к задаче.

Вальцуемая деталь в начале процесса лежит на двух крайних роликах (валках), имеющих диаметр D . Средний ролик (валок) диаметром d подводится до касания с верхом заготовки. Далее средний ролик (валок) опускается вниз на расстояние равное расчетному размеру H , включается привод вращения роликов, заготовка прокатывается, производится гибка металла, и на выходе получается деталь с заданным радиусом изгиба R ! Осталось дело за малым – правильно, быстро и точно научиться рассчитывать размер H . Этим и займемся.
Исходные данные:
1. Диаметр подвижного верхнего ролика (валка) /справочно/ d в мм записываем
в ячейку D3: 120
2. Диаметр опорных с приводом вращения крайних роликов (валков) D в мм пишем
в ячейку D4: 150
3. Расстояние между осями опорных крайних роликов (валков) A в мм вводим
в ячейку D5: 500
4. Высоту сечения детали h в мм заносим
в ячейку D6: 36
5. Внутренний радиус изгиба детали по чертежу R в мм заносим
в ячейку D7: 600

Расчеты и действия:
6. Вычисляем расчетную вертикальную подачу верхнего ролика (валка) Hрасч в мм без учета пружинения
в ячейке D9: =D4/2+D6+D7- ((D4/2+D6+D7)^2- (D5/2)^2)^(½) =45,4
Hрасч = D /2+ h + R — (( D /2+ h + R )^2- ( A /2)^2)^(½)
7. Настраиваем вальцы на этот размер Hрасч и делаем первый прогон заготовки. Измеряем или высчитываем по хорде и высоте сегмента получившийся в результате внутренний радиус, который обозначим R0 и записываем полученное значение в мм
в ячейку D10: 655
8. Вычисляем какой должна была бы быть расчетная теоретическая вертикальная подача верхнего ролика (валка) H0расч в мм для изготовления детали с радиусом R0 без учета пружинения
в ячейке D11: =D4/2+D6+D10- ((D4/2+D6+D10)^2- (D5/2)^2)^(½) =41,9
H0расч = D /2+ h + R0 — (( D /2+ h + R0 )^2- ( A /2)^2)^(½)
9. Но деталь с внутренним радиусом изгиба R0 получилась при опущенном верхнем валке на размер Hрасч, а не H0расч. Считаем поправку на обратное пружинение x в мм
в ячейке D12: =D9-D11 =3,5
x = Hрасч — H0расч
10. Так как радиусы R и R0 имеют близкие размеры, то можно с достаточной степенью точности принять эту же величину поправки x для определения окончательного фактического расстояния H , на которое необходимо подать вниз верхний ролик (валок) для получения на вальцованной детали внутреннего радиуса R .
Вычисляем окончательную расчетную вертикальную подачу верхнего ролика (валка) H в мм c учетом пружинения
в ячейке D13: =D9+D12 =48,9
H = Hрасч+ x
Задача решена! Первая деталь из партии изготовлена за 2 прохода! Найдено местоположение среднего ролика (валка).
Особенности и проблемы гибки металла на вальцах.
Да, как было бы всё красиво и просто – надавил, прогнал – деталь готова, но есть несколько «но»…
1. При вальцовке деталей с малыми радиусами в целом ряде случаев нельзя получить необходимый радиус R за один проход по причине возможности возникновения деформаций, гофр и надрывов в верхних (сжимаемых) и нижних (растягиваемых) слоях сечения заготовки. В таких случаях назначение технологом нескольких проходов обусловлено технологической особенностью конкретной детали. И это не исключительные случаи, а весьма распространенные!
2. Одномоментная без прокаток подача среднего ролика (валка) на большое расстояние H может быть недопустимой из-за возникновения значительных усилий, перегружающих сверх допустимой нормы механизм вертикального перемещения вальцев. Это может вызвать поломку станка. В аналогичной ситуации перегрузки при этом оказаться может и привод вращения роликов (валков)!
3. Концы заготовки, если их предварительно не подогнуть, например, на прессе, останутся прямолинейными участками при гибке на трехвалковых вальцах! Длина прямолинейных участков L чуть больше половины расстояния между нижними роликами А /2.
4. При движении среднего ролика (валка) вниз в сечении заготовки, подверженном изгибу, постепенно нарастают нормальные напряжения, которые вызывают вначале пружинную деформацию. Как только напряжения в крайних верхних и нижних волокнах сечения достигнут предела текучести материала детали σт , начнется пластическая деформация – то есть начнется процесс гибки. Если средний ролик (валок) отвести обратно вверх до начала возникновения пластической деформации, то заготовка отпружинит следом и сохранит свое первоначальное прямолинейное состояние! Именно эффект обратного пружинения вынуждает увеличить размер вертикальной подачи Hрасч на величину x , так как участки заготовки отпружинивают и частично распрямляются, выходя из зоны гибки, расположенной между роликами (валками).
Мы нашли эту поправку x опытным путем. Обратное пружинение или остаточную кривизну детали можно рассчитать, но это непростая задача. Кроме величины предела текучести материала σт значимую роль при решении этого вопроса играет момент сопротивления изгибу поперечного сечения вальцуемого элемента Wx . А так как часто профили особенно из алюминиевых сплавов имеют весьма замысловатое поперечное сечение, то расчет момента сопротивления Wx выливается в отдельную непростую задачу. К тому же и фактическое значение предела текучести σт часто значительно колеблется даже у образцов, вырезанных для испытаний из одного и того же листа или одного и того же куска профиля.
В предложенной методике сделана попытка уйти от определения обратного пружинения «методом научного тыка». Для пластичных материалов, например алюминиевых сплавов, значение x будет очень небольшим. Для сталей – в зависимости от марки, конечно, немного больше.
Вопросы, касающиеся гибки металла, рассматриваются так же в целом ряде весьма популярных у читателей этого блога статей: «Расчет усилия листогиба», «Расчет длины развертки», «Изготовление гнутого швеллера», «Всё о гнутом швеллере», «Всё о гнутом уголке».
Для получения информации о новых статьях и для скачивания рабочих файлов программ прошу Вас подписаться на анонсы в окне, расположенном в конце каждой статьи или в окне вверху страницы.
Не забывайте подтвердить подписку кликом по ссылке в письме, которое тут же придет к вам на указанную почту (может прийти в папку «Спам»).
Прошу уважающих труд автора скачивать файл с расчетом после подписки на анонсы статей!
Ссылка на скачивание файла: raschet-mestopolozheniia-rolika (xls 32,0KB).
ТЕХНОЛОГИЧЕСКИЕ ОСОБЕННОСТИ ГИБКИ МЕТАЛЛОВ
При этом методе между листом металла и стенками V-образной матрицы существует воздушный зазор, лист остается "в воздухе" и не соприкасается со стенками матрицы.
Пуансон воздействует на металл сверху в одной точке, а матрица только двумя точками вверху V-образного паза.
Геометрия гиба формируется только за счет глубины погружения пуансона в матрицу.
Ширина ручья на матрице чаще всего выбирается из расчета 10-15 толщин металла, а инструмент имеет угол намного более острый, чем деталь после гибки.
Преимущества «свободной гибки»:
- Высокая гибкость: без смены гибочных инструментов вы можете получить любой угол гибки, находящийся в промежутке между углом раскрытия V-образной матрицы.
- Меньшие затраты на инструмент, можно обойтись одним комплектом для многих задач.
- Меньшее требуемое усилие гибки по сравнению с другими методами гибки.
Недостатки «свободной гибки»:
- Менее точные углы. В связи с тем что инструмент воздействует на металл только в трех точках то заготовка может повести себя непредсказуемо и угол гиба по всей длине будет неравномерный,
- Меньшая точность повторений, на которую сильно влияют различия в качестве материала заготовок.
- Больший эффект обратного пружинения за счет большей упругой деформации.
- Меньшая универсальность и качество гибки. Раскрытие матрицы при свободной гибке 10-15 толщин листа, это является причиной увеличения минимального отгиба. Отсутствие соприкосновения со стенками матрицы является причиной деформации отверстий («выворот») расположенных близко к линии гиба.
В каких случаях «свободная гибка» предпочтительнее:
- Большая номенклатура изделий, мелкосерийное производство.
- Разные углы гибов (в том числе острые).
- Минимальные требования к точности и качеству гибов.
- Геометрия конечных деталей не содержит маленьких минимальных отгибов и допустимы внутренние радиусы гибов равные двум толщинам и более.
ГИБКА НА ОСНОВЕ
Данный метод гибки некоторые объединяют с «свободной гибкой», но у него много своих особенностей.
В отличии от классической «воздушной гибки» заготовка в самом конечном положении контактирует со стенками V-образного паза и нижней частью пуансона.
Требуемое усилие выше чем при «свободной гибке» до трех раз. Раскрытие матрицы выбирается из диапазона 6-10 толщин металла.
Преимущества «гибки на основе»:
- Более точные углы по сравнению с «воздушной гибкой», теоритические значения ±300.
- Меньший эффект обратного пружинения и большая повторяемость за счет большего воздействия на металл и уменьшения упругих деформаций. Несмотря на это пружинение немного остается, поэтому если необходимо получать на готовой детали 90°, то инструмент следует выбирать 88°-85°.
- Лучшее качество гибки: «выворот» отверстия уменьшается при достижении пуансоном нижнего положения, относительно небольшие раскрытия матриц позволяют делать небольшие минимальные отгибы и довольно точные внутренние радиусы равные от 1 до 2 толщин металла.
Недостатки «гибки на основе»:
- Большее требуемое усилие гибки по сравнению со «свободной», не применим для толстых металлов.
- Меньшая гибкость по сравнению с «воздушной гибкой», чтобы достичь всех преимуществ данного метода на другом профиле или угле необходим другой инструмент.
В каких случаях «гибка на основе» предпочтительнее:
- Ограниченная номенклатура изделий, мелкосерийное и серийное производство.
- Повышенные требования к точности и качеству гибов.
- Внутренние радиусы гибов должны быть от 1 до 2 толщин металла.
- Часто используется один угол гибов, например 90° и изредка более тупые.
- Оптимальные минимальные отгибы.
Данный метод заключается в максимальном пространства между пуансоном и матрицей в конечном положении.
Угол гиба определяется усилием и геометрией гибочного инструмента.
Давление продолжается даже при достижении нижней точки, за счет этого отсутствует упругая деформация, лист металла пластически деформируется под давлением инструмента.
Преимущества «чеканки»:
- Точность углов гиба, несмотря на разницу в толщине и свойствах материала.
- Маленький внутренний радиус, до 0,5 толщины металла, бывает недостижим другими способами.
- Обратное пружинение практически отсутствует, максимальная повторяемость.
- Доступные специльные исполнения, например Z-гибка, U-гибка, несколько гибов за один раз, сложные формы.
Недостатки «чеканки»:
- Максимальные требования по усилию, причем не только к станку, но и к инструменту и системе крепления.
- Отсутствие гибкости, один инструмент - один вид профиля.
- Только тонкий металл, в основном используют на толщинах до 2 мм.
- Повышенный износ инструмента и оборудования.
В каких случаях «чеканка» предпочтительнее:
- Крупносерийное производство.
- Самые высокие требования к точности и повторяемости.
- Внутренние радиусы гибов должны быть меньше толщины металла.
- Необходимо не зависеть от качества заготовок.
- Сложная форма гибов, которую не получить другими методами.
2. РАСЧЕТ УСИЛИЯ ДЛЯ ГИБКИ
Чтобы гибочный инструмент служил долго, необходимо ограничивать нагрузку на инструмент в соответствии с максимально допустимой. На инструменте этот параметр указывается в тоннах или килоньютонах на метр.
Важно понимать, что с уменьшением длины заготовки и инструмента уменьшается максимально допустимое номинальное усилие. Например, инструмент выдерживает нагрузку 60 тонн/метр, соответственно 10 сантиметров такого инструмента выдержит давление только 6 тонн.
Расчитать требуемое усилие для гибки металла можно только примерно, на практике используют таблицы или формулу.
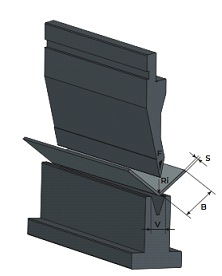
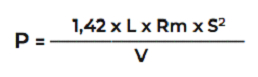
S - толщина металла, мм
V - раскрытие матрицы, мм
Ri - внутренний радиус гиба на детали, мм
В - минимальный отгиббез толщины металла при 90°, мм
Rm - предел прочности в кг/мм2
F - необходимое усилие, т/м
Формула расчета усилия:
1,42 - это коэффициент, учитывающий̆ трение заготовки о кромки матриц, у горячекатаного и несмазанного металла трение больше чем у холоднокатаного, если металл ржавый̆, то следует добавлять 10-15% к расчетному усилию.
L - длина заготовки, чтобы получить результат в тоннах длину надо указывать в метрах.
Таблица зависимости минимального отгиба от градуса гиба

Где В - минимальный отгиб без толщины металла при 90°, указанный в таблицах усилий
Пример расчета гибки листового металла
Гибка листового металла – процесс деформации формы заготовки путем изгиба под действием пресса на точку сгиба. Металлический лист помещают между двумя плитами или фигурными валками в зависимости от модели станка и подвергают контролируемой деформации. В дальнейшем полученная заготовка используется в качестве элемента для основного изделия.
Современное оборудование позволяет работать с металлами любых габаритов и толщины, придавая им сложный контур с несколькими углами. При необходимости из листового проката можно создать даже замкнутое изделие.

Почему важно в процессе гибки листа учитывать длину профиля и усилие пресса
Гибка листа при рабочих процессах всегда сопровождается деформациями, которые возникают в структуре металла. Внутренняя поверхность радиуса листа под действием профильного пресса сужается и образовывает складки, а внешняя поверхность – работает на разрыв и растяжение. Если выйти за пределы допустимых значений, в кристаллической решетке стали или алюминия появятся разрывы, которые значительно ухудшат свойства металла. В худшем случае, превышение допустимых нагрузок на точку сгиба может привести к полному разрыву материала.
Чтобы избежать подобного, специалисты выполняют предварительные расчеты предельных соотношений толщины металла, длины профиля и радиуса изгиба. В листогибах с ЧПУ расчеты выполняются автоматически. Оператору достаточно задать первичные параметры и оборудование самостоятельно произведет гибку листового металла под заданный угол.
Но такой метод не подойдет для малых и средних способов механизации. Здесь уже необходимо производить самостоятельные расчеты по специальным формулам и таблицам.
Даже если взять лист нержавеющей стали с точными размерами будущей заготовки, то после деформации готовое изделие получится на 7-9% короче. А это в точной работе недопустимо. Поэтому специалисты перед началом металлообработки выполняют предварительные расчеты по формулам.

Приведем примеры расчетов для ручной и полуавтоматической гибки
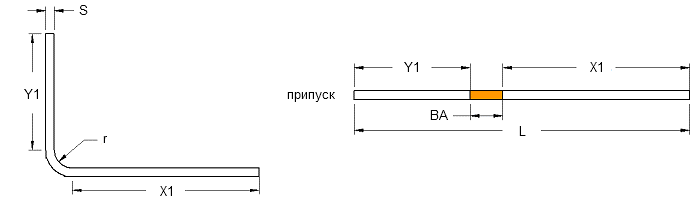
Размер длины заготовки определяется по формуле:
где
Y1 и X1 – длина прямых участков листового профиля;
φ – внешний угол;
r – радиус гиба;
K – коэффициент положения нейтральной линии (определяется по техническим таблицам)
S – толщина металла.
Для определения длины заготовки с несколькими углами перегиба в приведенную формулу добавляются суммы в скобках для каждого дополнительного угла. Расчет заготовки выполняется методом развертки с суммированием длины всех прямых полок Yn, Xn и добавления радиуса скривления.
Усилие пресса на заготовку при гибке листового металла определяется по формуле:
где
S – толщина листового профиля металла;
L – размер длины заготовки;
∂ʋ – предел прочности на растяжение (справочное значение);
V – развертка матрицы (технический параметр станка).
На практике специалисты используют готовые шаблоны и таблицы в зависимости от типа и размеров металлического профиля. Из таблиц выбираются точные параметры заготовки и подбираются максимально допустимые усилия пресса с углами деформации.
Расчеты по формулам используются только при работе с нестандартными заготовками и единичными заказами, где важно соблюсти размеры в точности до 0,1 мм.
Воспользуйтесь услугами специалистов
Нет времени разбираться самостоятельно? Компания «БиэМ» в рамках работ по гибке металла предоставляет услуги по гибке стального, оцинкованного и алюминиевого листа. Для обработки проката используются автоматические и полуавтоматические способы. В производственных цехах применяются листогибы с ЧПУ, которые позволяют обрабатывать черные металлы, нержавеющую сталь и алюминий с толщиной до 4 мм и общим габаритным размером до 3 м.
Изготовление заборов, в том числе с элементами холодной ковки от 6000 руб.
Читайте также:
