Как найти размер памяти любого массива numpy
Библиотека NumPy ( Numerical Python ) считается основной реализацией массивов Python. Она представляет высокопроизводительный, полнофункциональный тип n-мерного массива, который называется ndarray ( array ). Операции с array выполняются на два порядка быстрее, чем операции со списками. Многие популярные библиотеки data science, такие как pandas, SciPy, Keras и другие, построены на базе NumPy или зависят от нее.
1. Создание массива в Python
Создадим массив на основе списка. NumPy рекомендует импортировать модуль numpy под именем np , чтобы к его компонентам можно было обращаться с префиксом " np ".
Приведем пример создания массива на основе списка из трех строк и трех столбцов:
>>> b = [[5, 6, 10], [25, 64, 17], [14, 25, 14]]
>>> mas = np.array (b)
>>> mas
array([[ 5, 6, 10],
[25, 64, 17],
[14, 25, 14]])
NumPy автоматически форматирует array на основание количества их измерений и выравнивает столбцы в каждой строке.
Список так же можно передавать напрямую переменной:
>>> numbers = np.array ([ 1, 5, 47, 78])
>>> numbers
array([ 1, 5, 47, 78])
2. Атрибуты array
2.1. Определение типа элементов array
Для проверки типа элемента array можно воспользоваться атрибутом dtype :
2.2. Определение размерности array
Для определения размерности существует атрибут ndim , который содержит количество измерений array . Атрибут shape содержит кортеж, определяющий размерность array .
>>> import numpy as np
>>> numbers_1 = np.array ([[5, 7, 45], [14, 7, 9]])
>>> numbers_1. ndim
2
>>> numbers_1. shape
(2, 3)
В примере numbers_1 состоит из двух строк и трех столбцов.
2.3. Определение количества и размера элементов
Количество элементов в массиве можно получить с помощью атрибута size.
>>> import numpy as np
>>> numbers_1 = np.array ([[5, 7, 45], [14, 7, 9]])
>>> numbers_1. size
6
Количество байтов, необходимое для хранения элементов можно получить из атрибута itemsize .
>>> numbers_1. itemsize
4
Для компиляторов C с 32-разрядным int, размер равен 4. Если у вас 64-разрядный, у вас будет равен 8.
2.4. Перебор элементов array
Для перебора многомерной коллекции array можно воспользоваться циклом for:
Если вы хотите получить все результаты в одно строку, можно воспользоваться атрибутом flat :
3. Создание массивов в Python по диапазонам
NumPy представляет множество функций для создания массивов в заданном диапазоне. Разберем самые распространённые.
3.1. Создание диапазонов функцией arange
В библиотеке NumPy существует функция arange для создания целочисленных диапазонов, аналогичной встроенной функции range в Python.
>>> import numpy as np
>>> np. arange (7)
array([0, 1, 2, 3, 4, 5, 6])
>>> np. arange (5, 10)
array([5, 6, 7, 8, 9])
>>> np. arange (100, 10, -10)
array([100, 90, 80, 70, 60, 50, 40, 30, 20])
При создании коллекций array вы можете воспользоваться встроенной функции Python range, но рекомендуется использовать именно arange , так как она оптимизирована для array . Все свойства arange аналогичны функции range.
3.2. Создание диапазонов чисел с плавающей точкой функцией linspace
Для создания диапазонов чисел с плавающей точкой можно воспользоваться функцикй limspace библиотеки NumPy.
>>> import numpy as np
>>> np. linspace (1.0, 2.0, num=5)
array([1. , 1.25, 1.5 , 1.75, 2. ])
>>> np. linspace (1.0, 5.0, num=10)
array([1. , 1.44444444, 1.88888889, 2.33333333, 2.77777778, 3.22222222, 3.66666667, 4.11111111, 4.55555556, 5. ])
В функции linspace первые два аргумента определяют начальное и конечное значение диапазона. Важно: конечное значение включается в array . Ключевой аргумент num необязательный. Он задает количество равномерно распределенных генерируемых значений. По умолчанию num = 50 .
3.3. Изменение размерности array методом reshape
Методом reshape вы можете преобразовать одномерную коллекцию в многомерную. В примере создадим коллекцию array с помощью arange со значениями от 1 до 36 и с помощью метода reshape преобразуем ее в структуру из 6 строк и 6 столбцов.
>>> import numpy as np
>>> np.arange(1, 37). reshape (6, 6)
array([[ 1, 2, 3, 4, 5, 6],
[ 7, 8, 9, 10, 11, 12],
[13, 14, 15, 16, 17, 18],
[19, 20, 21, 22, 23, 24],
[25, 26, 27, 28, 29, 30],
[31, 32, 33, 34, 35, 36]])
>>> np.arange(1, 37). reshape (4, 9)
array([[ 1, 2, 3, 4, 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14, 15, 16, 17, 18],
[19, 20, 21, 22, 23, 24, 25, 26, 27],
[28, 29, 30, 31, 32, 33, 34, 35, 36]])
Во втором примере мы преобразовали в структуру 4 строк и 9 столбцов.
Размерность можно изменять для любой коллекции array , но при условии, что количество новой версии не будет отличаться от оригинала. Например, коллекцию из шести элементов, можно преобразовать в коллекцию 3*2 или 2*3. В нашем примере мы преобразовали коллекцию из 36 элементов в коллекцию 6*6 и 4*9. В случае неправильного преобразования, вы получите ошибку ValueError .
3.4. Заполнение array конкретными значениями. Функции zeros , ones , full
Функция zeros создает коллекцию содержащие 0. Первым аргументом должно быть целое число или кортеж целых чисел.
>>> import numpy as np
>>> np. zeros (7)
array([0., 0., 0., 0., 0., 0., 0.])
>>> np. zeros ((3, 3))
array([[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]])
Функция ones создает коллекцию содержащие 1.
>>> import numpy as np
>>> np. ones ((3, 3))
array([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
По умолчанию функции zeros и ones создают коллекции array, содержащие значения float . Для изменения типа значения можно задать аргумент dtype :
>>> import numpy as np
>>> np. ones ((3, 3), dtype=int )
array([[1, 1, 1],
[1, 1, 1],
[1, 1, 1]])
>>> np. zeros ((3, 3), dtype=int )
array([[0, 0, 0],
[0, 0, 0],
[0, 0, 0]])
Функция full , возвращает элементы со значением и типом второго аргумента:
>>> import numpy as np
>>> np. full ((3, 4), 55)
array([[55, 55, 55, 55],
[55, 55, 55, 55],
[55, 55, 55, 55]])
>>> np. full ((2, 4), 21.2)
array([[21.2, 21.2, 21.2, 21.2],
[21.2, 21.2, 21.2, 21.2]])
3.5. Вывод больших коллекций array
При выводе больших коллекций array , NumPy исключает из вывода все строки и столбцы кроме первых трех и последних. Вместо исключенных данных проставляется знак многоточие.
>>> import numpy as np
>>> np.arange(1, 100001).reshape(100, 1000)
array([[ 1, 2, 3, . 998, 999, 1000],
[ 1001, 1002, 1003, . 1998, 1999, 2000],
[ 2001, 2002, 2003, . 2998, 2999, 3000],
.
[ 97001, 97002, 97003, . 97998, 97999, 98000],
[ 98001, 98002, 98003, . 98998, 98999, 99000],
[ 99001, 99002, 99003, . 99998, 99999, 100000]])
4. Операторы array
4.1. Арифметические операции c массивами в Python
Арифметические операции с array выполняются поэлементно, то есть применяются к каждому элементу массива. Пример, если мы умножаем массив на 3, то каждый элемент будет умножен на 3. Так же и с остальными арифметическими операциями.
>>> import numpy as np
>>> numbers_1 = np.array ([[5, 7, 45], [14, 7, 9]])
>>> numbers_1 * 3
array([[ 15, 21, 135],
[ 42, 21, 27]])
>>> numbers_1 ** 3
array([[ 125, 343, 91125],
[ 2744, 343, 729]], dtype=int32)
>>> numbers_1
array([[ 5, 7, 45],
[14, 7, 9]])
Важно, что при арифметических операциях, возвращается новая коллекция array , исходный массив numbers_1 не изменяется.
А вот расширенное присваивание изменяет каждый элемент левого операнда:
>>> import numpy as np
>>> numbers_1 = np.array([[5, 7, 45], [14, 7, 9]])
>>> numbers_1 += 10
>>> numbers_1
array([[15, 17, 55],
[24, 17, 19]])
4.2. Арифметические операции между коллекциями array
С коллекциями array можно выполнять арифметические операции, если они имеют одинаковые размеры. Результатом будет новая коллекция array :
>>> import numpy as np
>>> numbers_1 = np.array ([[5, 7, 45], [14, 7, 9]])
>>> numbers_2 = np.array ([[8, 12, -35], [4, 12, 25]])
>>> numbers_1 * numbers_2
array([[ 40, 84, -1575],
[ 56, 84, 225]])
>>> numbers_1 - numbers_2
array([[ -3, -5, 80],
[ 10, -5, -16]])
4.3. Сравнение коллекция array
Коллекции array можно сравнивать как между собой, так и с отдельными значениями. Сравнение выполняется поэлементно.
>>> import numpy as np
>>> numbers_1 = np.array([2, 4, 6, 8, 10])
>>> numbers_2 = np.array([1, 5, 6, 7, 12])
>>> numbers_1 > numbers_2
array([ True, False, False, True, False])
>>> numbers_1 == numbers_2
array([False, False, True, False, False])
>>> numbers_1 >= 5
array([False, False, True, True, True])
В результате сравнений создаются коллекции array с логическими значениями ( True или False), каждое из которых означает результат сравнения каждого элемента.
5. Вычислительные методы NumPy
При помощи различных методов мы можем проводить арифметические операции внутри коллекций, вычислить сумму всех элементов или найти наибольше значение. Приведем пример основных методов:
>>> import numpy as np
>>> grades = np.array([[3, 4, 5, 4], [2, 5, 4, 5], [5, 5, 4, 5]])
>>> grades
array([[3, 4, 5, 4],
[2, 5, 4, 5],
[5, 5, 4, 5]])
>>> grades. min()
2
>>> grades. max()
5
>>> grades. sum()
51
>>> grades. mean()
4.25
>>> grades. std()
0.924211375534118
>>> grades. var()
0.8541666666666666
Метод min() и max() находит наименьшее и наибольшее значение. Метод sum() - вычисляет сумму всех элементов, mean() - математическое ожидание, std() - стандартное отклонение, var() - дисперсию.
Эти методы могут применяться к конкретным осям array. К примеру, нам нужно вычислить средний бал по предмету. Для это в метод добавляется аргумент axis , который позволяет проводить вычисление по строкам или столбцам.
>>> grades.mean( axis=0 )
array([3.33333333, 4.66666667, 4.33333333, 4.66666667])
>>> grades.mean( axis=1 )
array([4. , 4. , 4.75])
Если axis=0, выполняется вычисления по всем значениям строк внутри каждого столбца.
Если axis=1, выполняется вычисления со всеми значениями столбца внутри каждой отдельной строки.
6. Индексирование и сегментация массивов в Python
Для одномерных коллекций array применяются, операции сегментации и индексирования, описанные в разделе "Сегментация последовательностей в Python". Ниже разберем сегментацию с двумерными коллекциями array.
Выбор элемента двумерной коллекции array
Для выбора элемента двумерной коллекции array укажите кортеж с индексами строки и столбца элемента в квадратных скобках.
Выбор подмножества строк двумерной коллекции array
Для выбора одной строки укажите в квадратных скобках только один индекс:
>>> grades[ 2 ]
array([5, 5, 4, 5])
Для выбора нескольких строк используйте синтаксис сегмента:
>>> grades[ 1:3 ]
array([[2, 5, 4, 5],
[5, 5, 4, 5]])
Для выбора нескольких несмежных строк используйте список индексов строк:
>>> grades[[ 1, 3 ]]
array([[2, 5, 4, 5],
[5, 4, 5, 3]])
Выбор подмножества столбцов двумерной коллекции array
Для выбора подмножества столбцов следует указать кортеж, в котором указаны выбираемые строки и столбцы:
>>> grades[ :, 1 ]
array([4, 5, 5, 4])
Двоеточие указывает какие строки в столбце должны выбираться. В нашем случает " : " является сегментом и выбираются все строки. После запятой мы указали 1, значит выбрали столбец номер два.
Для выбора нескольких смежных столбцов используется синтаксис сегмента:
Для выбора конкретных столбцов используйте список индексов этих строк:
>>> grades[:, [0, 2, 3] ]
array([[3, 5, 4],
[2, 4, 5],
[5, 4, 5],
[5, 5, 3]])
7. Глубокое копирование. Метод copy
В случае если вам необходимо создать новую коллекцию с аналогичными данными, можно воспользоваться методом copy . Метод copy коллекций array возвращает новый объект array с глубокой копией данных объекта исходной коллекции.
>>> import numpy as np
>>> numbers_1 = np.array([21, 25, 12, 1, 78])
>>> numbers_1
array([21, 25, 12, 1, 78])
>>> numbers_2 = numbers_1. copy()
>>> numbers_2
array([21, 25, 12, 1, 78])
В итоге мы получили новый массив numbers_2, с которым далее мы можем работать, не изменяя основной массив.
8. Изменение размеров и транспонирование массива в Python
В NumPy существует много возможностей для изменения размера массивов.
8.1. Метод resize
Метод resize изменяет размер исходной коллекции array:
>>> import numpy as np
>>> numbers = np.array([21, 25, 12, 1, 78, 77])
>>> numbers
array([21, 25, 12, 1, 78, 77])
>>> numbers. resize(3, 2)
>>> numbers
array([[21, 25],
[12, 1],
[78, 77]])
8.2. Методы flatten и ravel
- Метод flatten выполняет глубокое копирование данных исходной коллекции
>>> import numpy as np
>>> numbers = np.array([21, 25, 12, 1, 78])
>>> numbers_fl = numbers. flatten()
>>> numbers_fl
array([21, 25, 12, 1, 78])
Чтобы проверить что numbers и numbers_fl не используют общие данные изменим элемент numbers_fl и выведем оба массива:
>>> numbers_fl[ 0 ] = 77
>>> numbers_fl
array([ 77 , 25, 12, 1, 78])
>>> numbers
array([21, 25, 12, 1, 78])
Значение в numbers_fl изменилось, значит массивы уже не связаны между собой.
- метод ravel создает представление (поверхностную копию) исходной коллекции array, которое использует общие данные.
>>> numbers
array([21, 25, 12, 1, 78])
>>> numbers_ra = numbers. ravel()
>>> numbers_ra
array([21, 25, 12, 1, 78])
Чтобы проверить использование общих данных, изменим один элемент numbers_ra:
>>> numbers_ra[ 0 ] = 125
>>> numbers_ra
array([ 125 , 25, 12, 1, 78])
>>> numbers
array([ 125 , 25, 12, 1, 78])
В результате значения поменялись в обоих массивах.
8.3. Транспонирование строк и столбцов
С помощью атрибута T вы можете быстро транспонировать строки и столбцы маcсива, то есть сделать так чтобы строки стали столбцами, а столбцы строками.
>>> import numpy as np
>>> numbers = np.array([[45, 65, 48], [78, 45, 62]])
>>> numbers
array([[45, 65, 48],
[78, 45, 62]])
>>> numbers. T
array([[45, 78],
[65, 45],
[48, 62]])
Транспонирование не изменяет исходную коллекцию array.
8.4. Горизонтальное и вертикальное дополнение. Функции hstack и vstack
Добавление новых строк или столбцов, называется горизонтальным или вертикальным дополнением. Допустим у нас есть две коллекции array, и мы хотим объединить их в одну. Для этого можно воспользоваться функцией hstack() из библиотеки NumPy. Функцие hstack() передается кортеж с объединяемыми коллекциями:
>>> import numpy as np
>>> numbers_1 = np.array([21, 25, 12, 1, 78])
>>> numbers_2 = np.array([17, 54, 55, 24, 78])
>>> np. hstack (( numbers_1, numbers_2 ))
array([21, 25, 12, 1, 78, 17, 54, 55, 24, 78])
В случае если нам требуется объединить массивы добавлением, можно воспользоваться функцией vstack() :
>>> np. vstack (( numbers_1, numbers_2 ))
array([[21, 25, 12, 1, 78],
[17, 54, 55, 24, 78]])
Здравствуйте! Я продолжаю работу над пособием по python-библиотеке NumPy.
В прошлой части мы научились создавать массивы и их печатать. Однако это не имеет смысла, если с ними ничего нельзя делать.
Сегодня мы познакомимся с операциями над массивами.
Базовые операции
Математические операции над массивами выполняются поэлементно. Создается новый массив, который заполняется результатами действия оператора.
Для этого, естественно, массивы должны быть одинаковых размеров.
Также можно производить математические операции между массивом и числом. В этом случае к каждому элементу прибавляется (или что вы там делаете) это число.
NumPy также предоставляет множество математических операций для обработки массивов:
Полный список можно посмотреть здесь.
Многие унарные операции, такие как, например, вычисление суммы всех элементов массива, представлены также и в виде методов класса ndarray.
По умолчанию, эти операции применяются к массиву, как если бы он был списком чисел, независимо от его формы. Однако, указав параметр axis, можно применить операцию для указанной оси массива:
Индексы, срезы, итерации
Одномерные массивы осуществляют операции индексирования, срезов и итераций очень схожим образом с обычными списками и другими последовательностями Python (разве что удалять с помощью срезов нельзя).
У многомерных массивов на каждую ось приходится один индекс. Индексы передаются в виде последовательности чисел, разделенных запятыми (то бишь, кортежами):
Когда индексов меньше, чем осей, отсутствующие индексы предполагаются дополненными с помощью срезов:
b[i] можно читать как b[i, <столько символов ':', сколько нужно>]. В NumPy это также может быть записано с помощью точек, как b[i, . ].
Например, если x имеет ранг 5 (то есть у него 5 осей), тогда
- x[1, 2, . ] эквивалентно x[1, 2, :, :, :],
- x[. , 3] то же самое, что x[:, :, :, :, 3] и
- x[4, . , 5, :] это x[4, :, :, 5, :].
Итерирование многомерных массивов начинается с первой оси:
Однако, если нужно перебрать поэлементно весь массив, как если бы он был одномерным, для этого можно использовать атрибут flat:
Манипуляции с формой
Как уже говорилось, у массива есть форма (shape), определяемая числом элементов вдоль каждой оси:
Форма массива может быть изменена с помощью различных команд:
Порядок элементов в массиве в результате функции ravel() соответствует обычному "C-стилю", то есть, чем правее индекс, тем он "быстрее изменяется": за элементом a[0,0] следует a[0,1]. Если одна форма массива была изменена на другую, массив переформировывается также в "C-стиле". Функции ravel() и reshape() также могут работать (при использовании дополнительного аргумента) в FORTRAN-стиле, в котором быстрее изменяется более левый индекс.
Метод reshape() возвращает ее аргумент с измененной формой, в то время как метод resize() изменяет сам массив:
Если при операции такой перестройки один из аргументов задается как -1, то он автоматически рассчитывается в соответствии с остальными заданными:
Объединение массивов
Несколько массивов могут быть объединены вместе вдоль разных осей с помощью функций hstack и vstack.
hstack() объединяет массивы по первым осям, vstack() — по последним:
Функция column_stack() объединяет одномерные массивы в качестве столбцов двумерного массива:
Аналогично для строк имеется функция row_stack().
Разбиение массива
Используя hsplit() вы можете разбить массив вдоль горизонтальной оси, указав либо число возвращаемых массивов одинаковой формы, либо номера столбцов, после которых массив разрезается "ножницами":
Функция vsplit() разбивает массив вдоль вертикальной оси, а array_split() позволяет указать оси, вдоль которых произойдет разбиение.
Копии и представления
При работе с массивами, их данные иногда необходимо копировать в другой массив, а иногда нет. Это часто является источником путаницы. Возможно 3 случая:
Вообще никаких копий
Простое присваивание не создает ни копии массива, ни копии его данных:
Python передает изменяемые объекты как ссылки, поэтому вызовы функций также не создают копий.
Представление или поверхностная копия
Разные объекты массивов могут использовать одни и те же данные. Метод view() создает новый объект массива, являющийся представлением тех же данных.
Пакет numpy предоставляет $n$-мерные однородные массивы (все элементы одного типа); в них нельзя вставить или удалить элемент в произвольном месте. В numpy реализовано много операций над массивами в целом. Если задачу можно решить, произведя некоторую последовательность операций над массивами, то это будет столь же эффективно, как в C или matlab — львиная доля времени тратится в библиотечных функциях, написанных на C .
Замечание. Модуль numpy.random не рассматривается целенаправленно. Вместо него рассмотри модуль scipy.stats , который больше подходит под вероятностно-статистические задачи.
Можно преобразовать список в массив.
print печатает массивы в удобной форме.
Класс ndarray имеет много методов.
Наш массив одномерный.
В $n$-мерном случае возвращается кортеж размеров по каждой координате.
size — это полное число элементов в массиве; len — размер по первой координате (в 1-мерном случае это то же самое).
numpy предоставляет несколько типов для целых ( int16 , int32 , int64 ) и чисел с плавающей точкой ( float32 , float64 ).
Массив чисел с плавающей точкой.
Точно такой же массив.
Индексировать массив можно обычным образом.
Массивы — изменяемые объекты.
Массивы, разумеется, можно использовать в for циклах. Но при этом теряется главное преимущество numpy — быстродействие. Всегда, когда это возможно, лучше использовать операции над массивами как едиными целыми.
Упражнение: создайте numpy-массив, состоящий из первых пяти простых чисел, выведите его тип и размер.
Решение:
Массивы, заполненные нулями или единицами. Часто лучше сначала создать такой массив, а потом присваивать значения его элементам.
Если нужно создать массив, заполненный нулями, длины и типа другого массива, то можно использовать конструкцию
Функция arange подобна range . Аргументы могут быть с плавающей точкой. Следует избегать ситуаций, когда (конец-начало)/шаг — целое число, потому что в этом случае включение последнего элемента зависит от ошибок округления. Лучше, чтобы конец диапазона был где-то посредине шага.
Последовательности чисел с постоянным шагом можно также создавать функцией linspace . Начало и конец диапазона включаются; последний аргумент — число точек.
Упражнение: создайте и выведите последовательность чисел от 10 до 20 с постоянным шагом, длина последовательности - 21.
Решение:
Последовательность чисел с постоянным шагом по логарифмической шкале от $10^0$ до $10^1$.
Арифметические операции проводятся поэлементно.
Когда операнды разных типов, они пиводятся к большему типу.
Библиотека numpy содержит элементарные функции, которые тоже применяются к массивам поэлементно. Они называются универсальными функциями ( ufunc ).
Один из операндов может быть скаляром, а не массивом.
Сравнения дают булевы массивы.
Кванторы "существует" и "для всех".
Модификация на месте.
При выполнении операций над массивами деление на 0 не возбуждает исключения, а даёт значения np.nan или np.inf .
Сумма и произведение всех элементов массива; максимальный и минимальный элемент; среднее и среднеквадратичное отклонение.
Имеются встроенные функции
Иногда бывает нужно использовать частичные (кумулятивные) суммы. В наших курсах такое может пригодится.
Функция sort возвращает отсортированную копию, метод sort сортирует на месте.
Расщепление массива в позициях 3 и 6.
Функции delete , insert и append не меняют массив на месте, а возвращают новый массив, в котором удалены, вставлены в середину или добавлены в конец какие-то элементы.
Есть несколько способов индексации массива. Вот обычный индекс.
Диапазон индексов. Создаётся новый заголовок массива, указывающий на те же данные. Изменения, сделанные через такой массив, видны и в исходном массиве.
Диапазон с шагом 2.
Массив в обратном порядке.
Подмассиву можно присвоить значение — массив правильного размера или скаляр.
Тут опять создаётся только новый заголовок, указывающий на те же данные.
Чтобы скопировать и данные массива, нужно использовать метод copy .
Можно задать список индексов.
Можно задать булев массив той же величины.
Упражнение:
1). Создайте массив чисел от $-2\pi$ до $2\pi$.
2). Посчитайте сумму поэлементных квадратов синуса и косинуса для данного массива.
3). С помощью np.all проверьте, что в ответе только единицы.
Решение:
Атрибуту shape можно присвоить новое значение — кортеж размеров по всем координатам. Получится новый заголовок массива; его данные не изменятся.
Можно растянуть в одномерный массив
Арифметические операции поэлементные
Поэлементное и матричное (только в Python >=3.5) умножение.
Упражнение: создайте матрицы $\begin -3 & 4 \\ 4 & 3 \end$ и $\begin 2 & 1 \\ 1 & 2 \end$. Посчитайте их поэлементное и матричное произведения.
Решение:
Умножение матрицы на вектор.
Если у вас Питон более ранней версии, то для работы с матрицами можно использовать класс np.matrix , в котором операция умножения реализуется как матричное умножение.
Внешнее произведение $a_=u_i v_j$
Двумерные массивы, зависящие только от одного индекса: $x_=u_j$, $y_=v_i$
Метод reshape делает то же самое, что присваивание атрибуту shape .
Цикл по строкам.
Можно построить двумерный массив из функции.
Соединение матриц по горизонтали и по вертикали.
Сумма всех элементов; суммы столбцов; суммы строк.
Аналогично работают prod , max , min и т.д.
След - сумма диагональных элементов.
Упражнение:
в статистике и машинном обучении часто приходится иметь с функцией $RSS$, которая вычисляется по формуле $\sum_^ (y_i - a_i)^2$, где $y_i$ — координаты одномерного вектора $y$, $a_i$ — координаты одномерного вектора $a$. Посчитайте $RSS$ для $y = (1, 2, 3, 4, 5), a = (3, 2, 1, 0, -1)$.
Решение:
Суммирование (аналогично остальные операции)
Выше при арифметических операциях с массивами, например, при сложении и умножении, мы перемножали массивы одинаковой формы. В самом простом случае операндами были одномерные массивы одинаковой длины.
Произошло поэлементное умножение, все элементы массива $a$ умножились на $2$. Но мы знаем, что это можно сделать проще, просто умножив массив на $2$.
На самом деле поведение будет аналогичным, если умножить одномерный массив на массив длины $1$.
В этом случае работает так называемый broadcasting. Один массив "растягивается", чтобы повторить форму другого.
Такой же эффект работает и для многомерных массивов. Если по какому-то измерению размер у одного массива равен $1$, а у другого — произвольный, то по этому измерению может произойти "рястяжение". Таким образом, массивы можно умножать друг на друга, если в измерениях, где они по размеру не совпадают, хотя бы у одного размер $1$. Для других поэлементных операций правило аналогично.
Важно отметить, что размерности сопоставляются справа налево. Если их количество не совпадает, что массивы меньшей размерности сначала дополняются слева размерностями 1. Например, при сложении массива размера $4 \times 3$ с массивом размера $3$ последний сначала преобразуется в массив размера $1 \times 3$.
Схематично проведенную операцию можно визуализировать следующим образом.
Если неединичные размерности справа не будут совпадать, то выполнить операцию уже не получится. Например, как приведено на схеме ниже.
Упражнение:
Подумайте, массив какого размера получится, если перемножить массив $4 \times 1 \times 3$ и массив $12 \times 1$. Убедитесь на практике в правильности вашего ответа.
Знать про broadcasting нужно, но пользоваться им надо с осторожностью. Многократное копирование массива при растяжении может привести к неэффективной работе программы по памяти. Особенно за этим приходится следить при работе с GPU.
Решение линейной системы $au=v$.
Собственные значения и собственные векторы: $a u_i = \lambda_i u_i$. l — одномерный массив собственных значений $\lambda_i$, столбцы матрицы $u$ — собственные векторы $u_i$.
Функция diag от одномерного массива строит диагональную матрицу; от квадратной матрицы — возвращает одномерный массив её диагональных элементов.
Все уравнения $a u_i = \lambda_i u_i$ можно собрать в одно матричное уравнение $a u = u \Lambda$, где $\Lambda$ — диагональная матрица с собственными значениями $\lambda_i$ по диагонали.
Поэтому $u^ a u = \Lambda$.
Найдём теперь левые собственные векторы $v_i a = \lambda_i v_i$. Собственные значения $\lambda_i$ те же самые.
Собственные векторы нормированы на 1.
Левые и правые собственные векторы, соответствующие разным собственным значениям, ортогональны, потому что $v_i a u_j = \lambda_i v_i u_j = \lambda_j v_i u_j$.
Упражнение:
в машинном обучении есть модель линейной регрессии, для которой "хорошее" решение считается по следующей формуле: $\widehat = (X^T \cdot X + \lambda \cdot I_n)^\cdot X^T y$. Вычислите $\widehat$ для $ X = \begin -3 & 4 & 1 \\ 4 & 3 & 1 \end$, $y = \begin 10 \\ 12 \end$, $I_n$ — единичная матрица размерности 3, $\lambda = 0.1$.
Решение:
Адаптивное численное интегрирование (может быть до бесконечности). err — оценка ошибки.
Получится такой файл
Теперь его можно прочитать
Посмотрим на простой пример — сумма первых $10^8$ чисел.
Немного улучшеный код
Код с использованием функций библиотеки numpy
Простой и понятный код работает в $30$ раз быстрее!
Посмотрим на другой пример. Сгенерируем матрицу размера $500\times1000$, и вычислим средний минимум по колонкам.
Простой код, но при этом даже использующий некоторые питон-функции
Замечание. Далее с помощью scipy.stats происходит генерация случайных чисел из равномерного распределения на отрезке $[0, 1]$. Этот модуль будем изучать в следующем ноутбуке.
Понятный код с использованием функций библиотеки numpy
Простой и понятный код работает в 1500 раз быстрее!
С помощью соглашения Эйнштейна о суммировании, многие общие многомерные линейные алгебраические операции с массивами могут быть представлены простым способом.
Если одна и та же буква в обозначении индекса встречается и сверху, и снизу, то такой член полагается просуммированным по всем значениям, которые может принимать этот индекс.
Например, выражение $c_j = a_i b^i_j$ понимается как $c_j = \sum_^n a_i b^i_j$.
Подобные операции часто возникают в анализе данных, в особенности при реализации байесовских методов.
В numpy такие операции реализует функция einsum , причем здесь не делается разницы между нижними и верхними индексами. Функция принимает на вход сигнатуру операции в виде текстовой строки и матрицы с данными.
Разберем на примере выше. В данном случае сигнатура имеет вид i,ji->j . Элементы сигнатуры последовательно означают следующее (тензор = многомерная матрица):
Визуально, данный массив выглядит следующим образом:
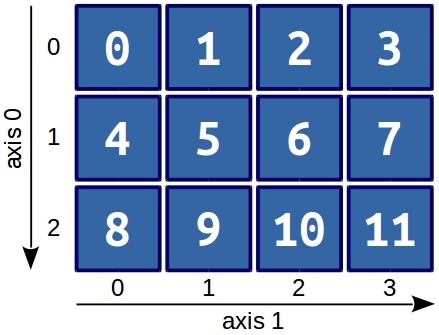
Глядя на картинку, становится понятно, что первая ось (и индекс соответственно) - это строки, вторая ось - это столбцы. Т.е. получить элемент 9 можно простой командой:
Снова можно подумать, что ничего нового - все как в стандартном Python. Да, так и есть, и, это круто!
Еще круто, то что NumPy добавляет к удобному и привычному синтаксису Python, весьма удобные трюки, например - транслирование массивов:
В данном примере, без всяких циклов, мы умножили каждый столбец из массива a на соответствующий элемент из массива b .
Т.е. мы как бы транслировали (в какой-то степени можно сказать - растянули) массив b по массиву a .
То же самое мы можем проделать с каждой строкой массива a :
В данном случае мы просто прибавили к массиву a массив-столбец c . И получили, то что хотели.
При работе с двумерными или трехмерными массивами, особенно с массивами большей размерности, становится очень важным удобство работы с элементами массива, которые расположены вдоль отдельных измерений - его осей.
Например, у нас есть двумерный массив и мы хотим узнать его минимальные элементы по строкам и столбцам.
Для начала создадим массив из случайных чисел и пусть, для нашего удобства, эти числа будут целыми:
Минимальный элемент в данном массиве это:
А вот минимальные элементы по столбцам и строкам:
Такое поведение заложено практически во все функции и методы NumPy:
Что насчет вычислений, их скорости и занимаемой памяти?
Для примера, создадим трехмерный массив:
Почему именно трехмерный?
На самом деле реальный мир вовсе не ограничивается таблицами, векторами и матрицами.
Еще существуют тензоры, кватернионы, октавы. А некоторые данные, гораздо удобнее представлять именно в трехмерном и четырехмерном представлении:
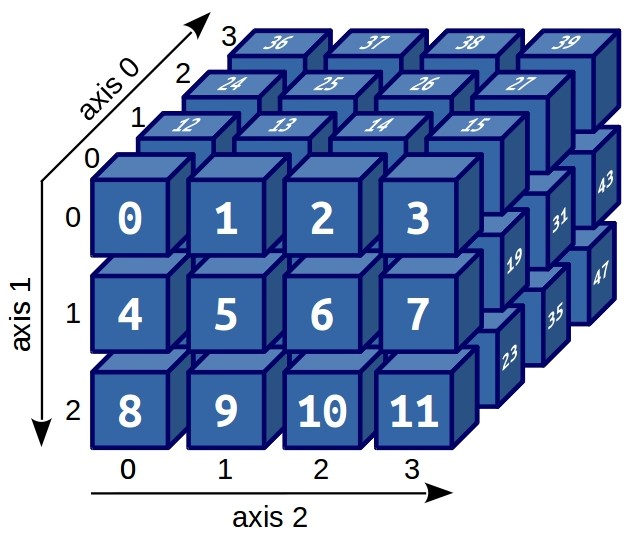
Визуализация (и хорошее воображение) позволяет сразу догадаться, как устроена индексация трехмерных массивов. Например, если нам нужно вытащить из данного массива число 31, то достаточно выполнить:
В самом деле, у массивов есть целый ряд важных атрибутов. Например, количество осей массива (его размерность), которую при работе с очень большими массивами, не всегда легко увидеть:
Массив a действительно трехмерный.
Но иногда становится интересно, а на сколько же большой массив перед нами. Например, какой он формы, т.е. сколько элементов расположено вдоль каждой оси? Ответить позволяет метод ndarray.shape :
Метод ndarray.size просто возвращает общее количество элементов массива:
Еще может встать такой вопрос - сколько памяти занимает наш массив?
Иногда даже возникает такой вопрос - влезет ли результирующий массив после всех вычислений в оперативную память?
Что бы на него ответить надо знать, сколько "весит" один элемент массива:
ndarray.itemsize возвращает размер элемента в байтах.
Теперь мы можем узнать сколько "весит" наш массив:
Итого - 384 байта. На самом деле, размер занимаемой массивом памяти, зависит не только от количества элементов в нем, но и от испльзуемого типа данных:
dtype('int64') - означает, что используется целочисленный тип данных, в котором для хранения одного числа выделяется 64 бита памяти.
Но если мы выполним какие-нибудь вычисления с массивом, то тип данных может измениться:
Теперь у нас есть еще один массив - массив b и его тип данных 'float64' - вещественные числа (числа с плавающей точкой) длинной 64 бита.
И так, массив может быть создан из обычного списка или кортежа Python с использованием функции array() .
Причем тип полученного массива зависит от типа элементов последовательности:
Функция array() преобразует последовательности последовательностей в двумерные массивы, а последовательности последовательностей, которые тоже состоят из последовательностей в трехмерные массивы.
То есть уровень вложенности исходной последовательности определяет размерность получаемого массива:
Очень часто возникает задача создания массива определенного размера, причем, чем заполнен массив абсолютно неважно.
В этом случае можно воспользоваться циклами или генераторами списков (кортежей), но NumPy для таких случаев предлагает более быстрые и менее затратные функции-заполнители.
Функция zeros заполняет массив нулями, функция ones - единицами, а функция empty - случайными числами, которые зависят от состояния памяти.
По умолчанию, тип создаваемого массива - float64 .
Для создания последовательностей чисел NumPy предоставляет функцию arange , которая возвращает одномерные массивы:
Если функция arange используется с аргументами типа float , то предсказать количество элементов в возвращаемом массиве не так-то просто.
Гораздо чаще возникает необходимость указания не шага изменения чисел в диапазоне, а количества чисел в заданном диапазоне.
Функция linspace , так же как и arange принимает три аргумента, но третий аргумент, как раз и указывает количество чисел в диапазоне.
Функция linspace удобна еще и тем, что может быть использована для вычисления значений функций на заданном множестве точек:
Чтобы быстрее разобраться с примерами печати массивов воспользуемся методом ndarray.reshape() , который позволяет изменять размеры массивов.
Одномерные массивы в NumPy печатаются в виде строк:
Двумерные массивы печатаются в виде матриц:
Трехмерные массивы печатаются в виде списка матриц, которые разделены пустой строкой:
Можете поэкспериментировать с печатью массивов большей размерности и вы убедитесь, что в ней довольно легко ориентироваться.
В случае, если массив очень большой (больше 1000 элементов), NumPy печатает только начало и конец массива, заменяя его центральную часть многоточием.
Если необходимо выводить весь массив целиком, то такое поведение печати можно изменить с помощью set_printoptions .
Занимаясь научными вычислениями, вы получаете результаты, которые должны быть обязательно сохранены.
Самый надежный способ хранения - это загрузка массивов с результатами в файл, так как их легко хранить и передавать.
Для данных нужд, NumPy предоставляет очень удобные инструменты, позволяющие производить загрузку и выгрузку массивов в файлы различных форматов, а также производить их сжатие, необходимое для больших массивов.
NumPy имеет два собственных формата файлов .npy - для хранения массивов без сжатия и .npz - для предварительного сжатия массивов.
Читайте также:


