Фронтальный треугольник как сделать
Рис.142
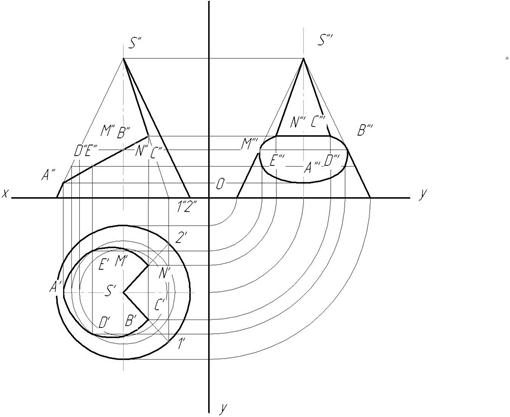
Вырез произведен двумя плоскостями. Одна проходит через вершину конуса и рассечет его поверхность по образующим. Вторая плоскость – фронтально-проецирующая, линия пересечения – часть эллипса, ограниченная прямой принадлежащей линии пересечения плоскостей.
1. Отметим фронтальные проекции характерных точек для построения выреза – А”, В”, С”, M",N" (рис. 143).
2. Точки D и Е выбраны произвольно для построения эллипса, т.к. линия среза от А до СN представляет собой часть эллипса.
3. Найдем горизонтальные проекции точек А, В, С, D, Е, N. Точки лежат на поверхности конуса, а значит, они лежат на линиях, принадлежащих поверхности конуса. Горизонтальные проекции точек М и В, D и E найдены на окружностях, принадлежащих поверхности конуса. Точки С и N – на образующих S1 и S2.
4. Соединяем полученные горизонтальные проекции. S’С’ и S’N‘ – прямые, C’, B’, D’, A’, E’, M’, N’ – кривая линия – часть эллипса (рис. 142).
Рис.143 Рис.144
Строим профильную проекцию конуса и профильные проекции точек. Соединяем их (рис.145).
Пример 2. Вырез на цилиндре (рис.146).
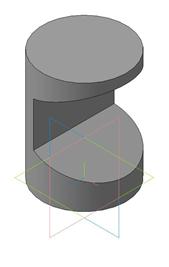
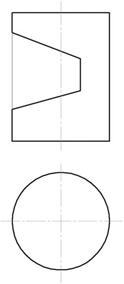
Вырез произведен тремя плоскостями. Наклонные фронтально-проецирующие плоскости рассекут цилиндр по части эллипса, ограниченного прямой. Плоскость, параллельная оси вращения, пересекает поверхность цилиндра по образующим.
1. Отметим на фронтальной проекции выреза фронтальные проекции A",F",G",K",L",P". Характерные точки D",E" ,M",N" – на оси симметрии цилиндра, B",C",T",V " – отмечены произвольно на линии, принадлежащей поверхности цилиндра. Все точки принадлежат боковой поверхности цилиндра, которая проецируется в окружность на горизонтальной плоскости проекций. Поэтому все горизонтальные проекции точек принадлежат этой окружности (рис.147).
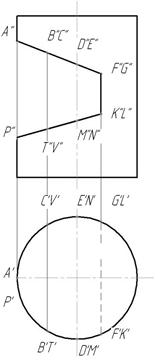
Рис.147
Найдем профильные проекции всех точек. Затем полученные точки соединяем. Линия GECABDF – часть эллипса, FK и GL отрезки прямых, GF и KL-отрезки прямых, LNVPTMK – часть эллипса (рис. 148).
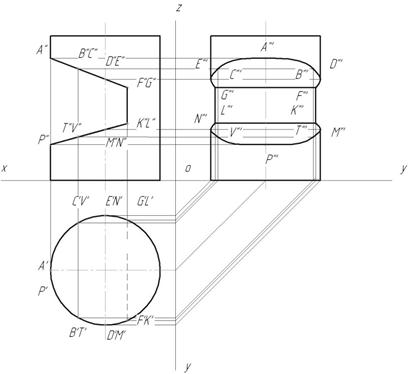
Рис.148
Пример 3. Вырез на призме (рис.149).
Рис.149 Hbc
Пример 4. Вырез на пирамиде (рис.150).
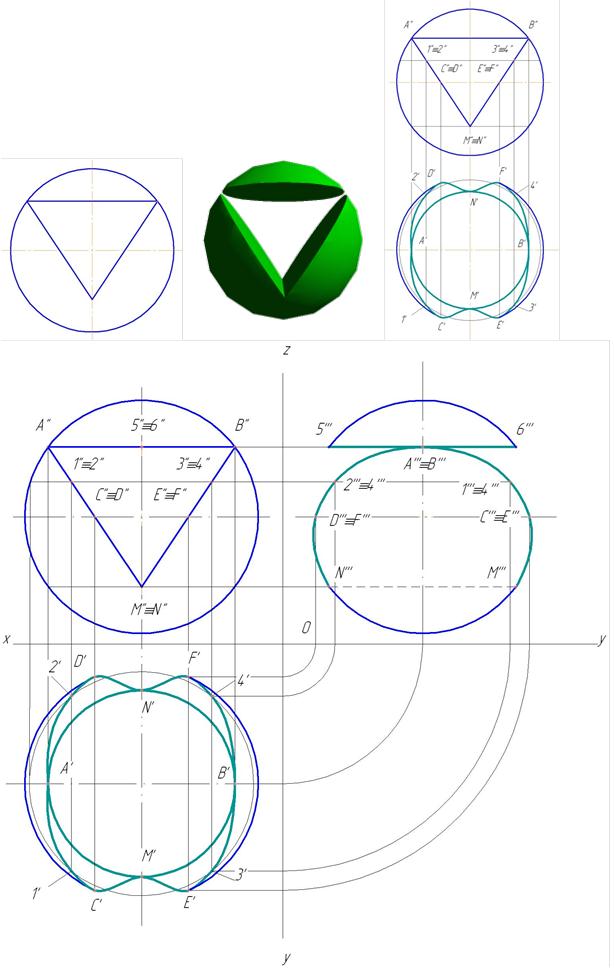
Пример 5. Вырез на сфере (рис. 151
p>
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: На стипендию можно купить что-нибудь, но не больше. 9122 – | 7289 – или читать все.
Отключите adBlock!
и обновите страницу (F5)
очень нужно




Пошаговое руководство решения задачи №6 — построение линии пересечения сферической поверхности от сквозного призматического выреза.
Необходимо построить линию пересечения сферической поверхности (шара) от сквозного призматического выреза, состоящего из четырех граней (проецирующих плоскостей). Фронтальная проекция линии пересечения заданных поверхностей (шара и многогранника) задана исходным чертежом, требуется построить ее в горизонтальную и профильную проекции.
Для решения такой задачи по начертательной геометрии необходимо знать:
— построение трех проекций сферической поверхности (шара) по заданным координатам, на комплексном чертеже;
— построение линии пересечения шаровой поверхности с гранным телом;
— частные случаи построения линии пересечения шаровой поверхности с проецирующей плоскостью.
Порядок решения Задачи

Рис.6.1
1. В правой части листа формата A3 наносятся оси координат и согласно варианту задания строится фронтальная, горизонтальная и профильная проекции сферы (шара) заданного радиуса.
По координатам точек, взятым из таблицы по своему варианту, наносятся вершины сквозного четырехгранного выреза во фронтальной проекции (рис.6.1).
2. Решение задачи заключается в построении горизонтальной и профильной проекции линии пересечения данного выреза.
Прежде чем приступить к построению этих проекций, необходимо вспомнить некоторые частные случаи сечений шаровой поверхности от проецирующей плоскости (сквозное отверстие можно рассматривать как гранное тело, образованное четырьмя плоскостями), а именно:
(а) если плоскость во фронтальной проекции рассекает шаровую поверхность параллельно экватору, то в горизонтальной проекции это сечение проецируется в виде окружности с радиусом, взятым в этом сечении от оси вращения шара до очерка, а в профильной проекции это сечение проецируется в виде прямой линии;
(b) если плоскость во фронтальной проекции рассекает шаровую поверхность перпендикулярно экватору, то в горизонтальной проекции это сечение проецируется в виде прямой линии, а в профильной — в виде окружности с радиусом, взятым тем же способом что и в первом случае;
(c) если плоскость во фронтальной проекции рассекает шаровую поверхность под некоторым (отличным от 0 и 90 градусов) углом к экватору, то в горизонтальной и фронтальной проекциях это сечение будет проецироваться в виде эллипса. Построение эллипса осуществляется по опорным (характерным) и некоторым промежуточным, взятым произвольно, точкам;
(d) все точки фронтальной проекции сферы, расположенные на очерке, в горизонтальной проекции будут проецироваться на экваторе, а в профильной — на главном меридиане;
(e) все точки фронтальной проекции сферы, расположенные на экваторе, в горизонтальной проекции будут проецироваться на очерке, а в профильной — на экваторе;
(f) все точки фронтальной проекции сферы, расположенные на главном меридиане, в горизонтальной проекции будут проецироваться также на главном меридиане, а в профильной — на очерке сферы.

Рис.6.2
3. С учетом приведенных частных случаев сечений построение выреза в горизонтальной и профильной проекциях не вызывает особых затруднений и начинается с определения характерных (опорных) точек сквозного выреза во фронтальной проекции. Этими точками являются А, В, С, D. Тогда берем проекцию стороны призмы B’C’ и рассматриваем ее как проецирующую плоскость ’, рассекающую шар параллельно экватору, — строим в горизонтальной проекции окружность с радиусом r1 взятым в этой плоскости, от оси шара до очерка. Проецируем на эту окружность точки B’ и C’, получаем B и C — их горизонтальные проекции. Вполне очевидно, что этих точек будет по две (точки входа и выхода), т.к. отверстие сквозное.
Аналогичным способом строится проекция сечения плоскости А’D’. Берется радиус от оси сферы до очерка (разумеется не до точки A’) и в горизонтальной проекции проводится окружность этим радиусом. Проецированием находятся проекции точек D (их будет две — точка входа и точка выхода) — D и D1 и промежуточной точки, расположенной на экваторе.

Рис.6.3
Сторона четырехугольника СD горизонтальной проекции проецируется в прямую линию, причем эта линия должна начинаться от очерка, т.к. во фронтальной проекции
она пересекает экватор шара и продолжается до точек С и D.

Рис.6.4
Горизонтальной проекцией сторон четырехугольника АВ будет эллипс, строим его по характерным (опорным) точкам. Проецируем точки, расположенные на меридиане, экваторе и очерке фронтальной проекции соответственно на меридиан, очерк и экватор горизонтальной проекции. Соединяя их по лекалу с уже имеющимися
проекциями точек B и B1, и получаем искомую проекцию эллипса.
4. Аналогичным способом строится третья профильная проекция данного выреза (вид слева), поэтому нет надобности в подробном изложении четырехугольника ВС и АD будут проецироваться в прямые линии, СD – в окружность, AB – в эллипс.

Рис.6.5
5. Заключительным этапом в решении задачи является определение видимости сторон сквозного выреза, которая определяется из расположения их на сопряженной плоскости проекций. Тогда видимыми точками и линиями в горизонтальной плоскости будут точки и линии, которые во фронтальной — расположены выше экватора и на профильной проекции видимыми будут точки и линии которые на фронтальной плоскости расположены левее меридианы.
Экватор и меридиан являются границами видимости. Точки и линии, расположенные ниже экватора и правее меридиана во фронтальной проекции, в горизонтальной и профильной проекциях будут невидимыми.
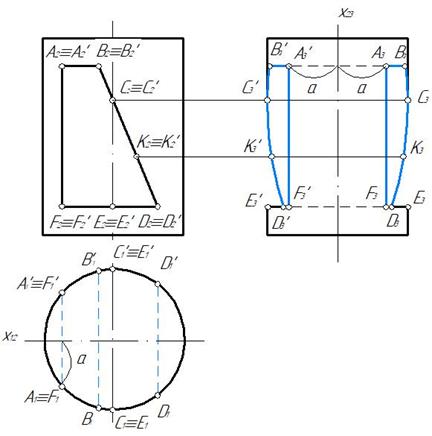
Пример 1. Построить три проекции цилиндра с вырезом (рис. 147).

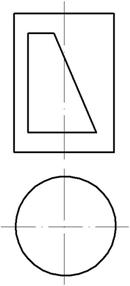
Отмечаем характерные точки выреза А, В, С, Д, Е, F, а также произвольную точку к для построения профильной проекции части эллипса. Горизонтальные проекции точек отмечаем на горизонтальном очерке цилиндра, так как горизонтальная проекция боковой поверхности цилиндра совпадает с горизонтальным очерком (рис .148)
Построение профильной проекции выреза показано на рис. 149. Для этого целесообразно ось x 12 провести через ось симметрии горизонтальной проекции,а ось x 23 через профильную ось симметрии.
Пример 2. Построить три проекции конуса с вырезом (рис. 150).

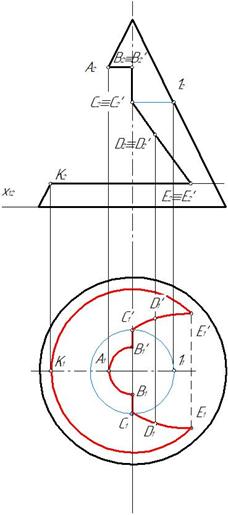
Отмечаем характерные точки вареза А, В, С, Е, K, а также произвольную точку D для построения части эллипса. Горизонтальные проекции точек отмечаем на образующих конуса и вспомогательных окружностях (рис. 151).
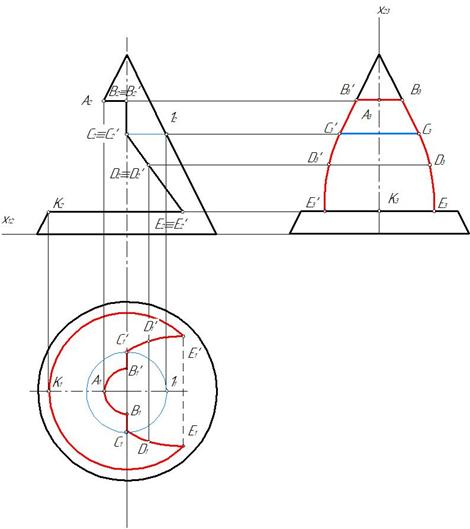
На рис. 152 показано построение профильной проекции конуса с вырезом.Для этого целесообразно ось x 12 провести через ось симметрии горизонтальной проекции, а ось x 23 через профильную ось симметрии.
Пример 3. Построить три проекции вырезе на призме (рис. 153).
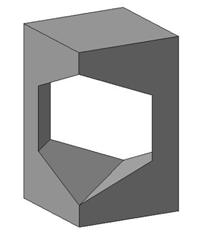
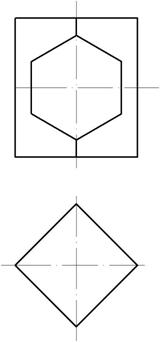
Решение показано на рис. 154
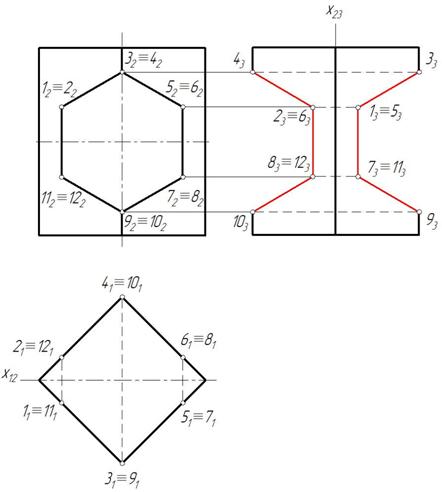
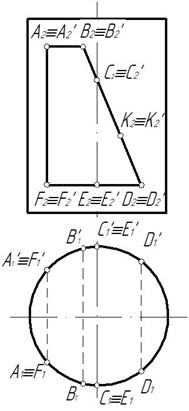
Пример 4. Построить три проекции выреза на пирамиде (рис. 155).
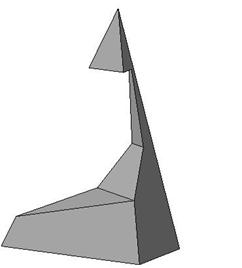
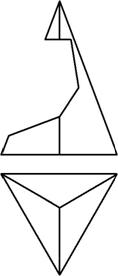
Отмечаем фронтальные проекции характерных точек выреза – это точки 12, 22, 32, 42, 52, 62. Для нахождения горизонтальных проекций точек 4 и 5 проводим по поверхности пирамиды две вспомогательные линии, параллельные основанию пирамиды ABC. Горизонтальные проекции этих линий являются треугольниками, параллельными горизонтальной проекции основания А1В1С1. На этих треугольниках отмечаем горизонтальные проекции точек 4 и 5 (рис. 156).
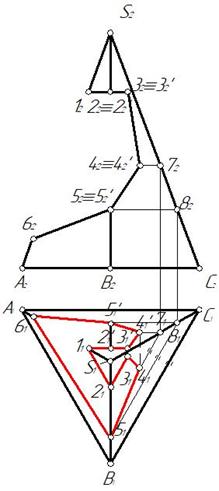
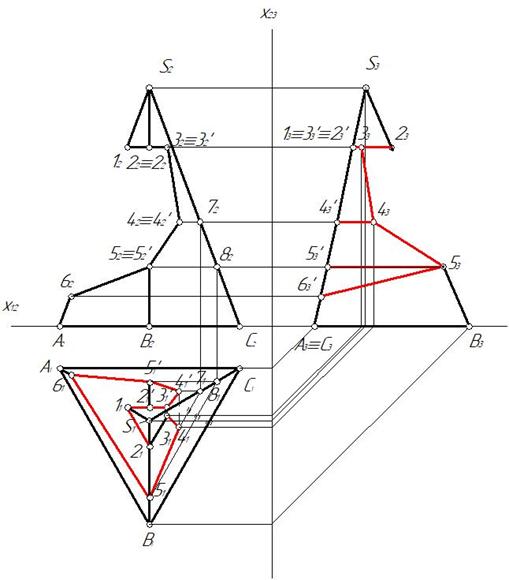
Затем строим профильную проекцию пирамиды и точек выреза. Для этого оси целесообразно провести как показано на рис. 157.
Пример 5. Построить три проекции выреза на сфере (рис. 158).
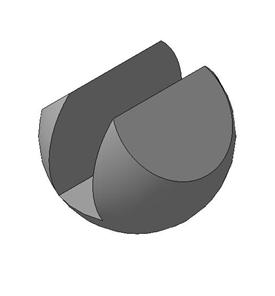
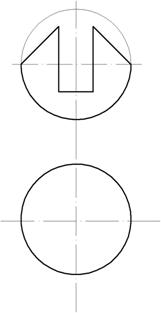
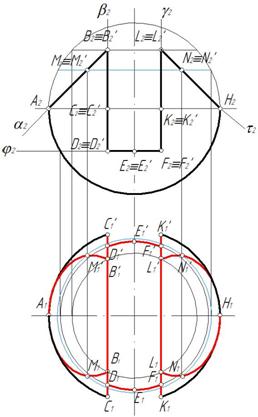
Вырез образован двумя фронтально-проецирующими плоскостями α и τ, горизонтальной плоскостью φ, двумя профильными плоскостями β и γ. Горизонтальная плоскость пересекает поверхность сферы по части окружности, ограниченной прямой. Фронтально-проецирующая плоскость пересекают поверхность сферы по окрухностям, которые на горизонтальной и профильной плоскости проецируются как части эллипсов. Профильная плоскость пересечет поверхность сферы по части окружности, которая на профильной плоскости спроецируется как часть окружности (рис. 159).
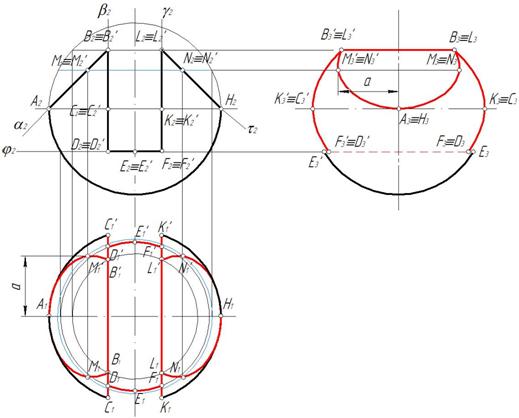
Построение профильной проекции показано на рис. 160
Метрические задачи

5. С помощью конкурирующих точек 4 и 5 определяем видимость треугольников на фронтальной плоскости проекций.

6. С помощью конкурирующих точек 6 и 7 определяем видимость треугольников на горизонтальной плоскости проекций.

7. В треугольнике ABC проводим горизонталь CL и плоскопараллельным перемещением относительно горизонтальной плоскости проекций располагаем горизонталь перпендикулярно фронтальной плоскости проекций.
Строим фронтальную проекцию треугольника ABC . Треугольник должен проецироваться в прямую линию.

8. Определяем действительную величину треугольника ABC и строим на нем линию пересечения MN.
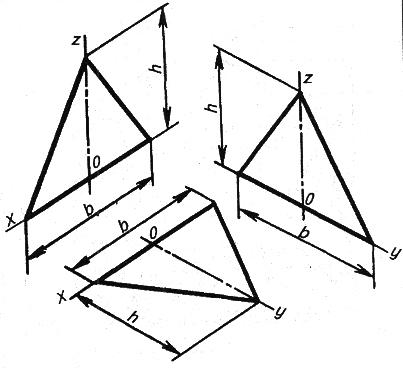
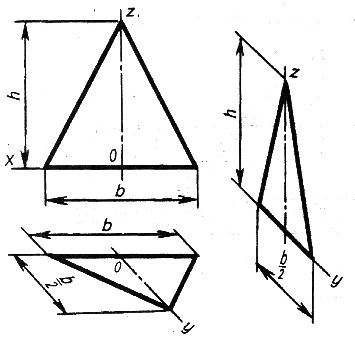
1. Треугольник расположен во фронтальной плоскости. По оси x откладываем по обе стороны от точки О отрезки b/2, равные в сумме b – стороне треугольника, а по оси z – его высоту h. Полученные точки соединяем отрезками прямых (рис.7,8).
2. Треугольник расположен в горизонтальной плоскости. По оси x откладываем от точки О отрезки b/2, равные в сумме b – стороне треугольника, а по оси y – его высоту h. Для изометрической проекции (рис.7) и половину его высоты
(h /2 ) – для фронтальной диметрии (рис.8). Полученные точки соединяем отрезками прямых.
3. Треугольник расположен в профильной плоскости. По оси y откладываем половину стороны (b/2) для фронтальной диметрической проекции и сторону b для изометрической, а по оси z – его высоту h (рис.7,8).
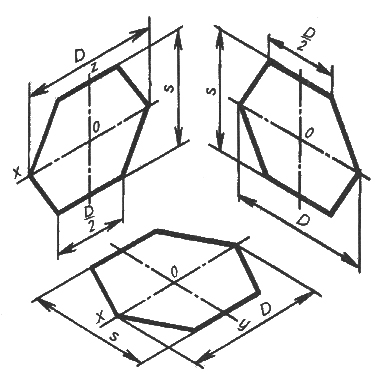
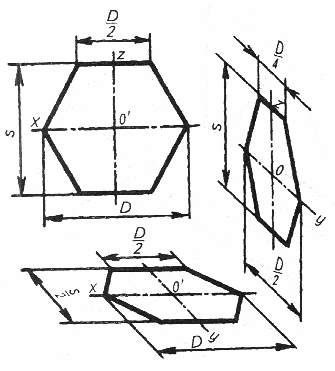
Построение аксонометрических проекций правильного шестиугольника:
1. Шестиугольник расположен во фронтальной плоскости. По оси х, симметрично точке О откладываем радиусы описанной окружности вокруг шестиугольника (D/2), равные размеру стороны шестиугольника, а по оси z, также симметрично точке О – отрезки S/2, равные половине расстояния между противоположными сторонами шестиугольника. Через точки, полученные на оси z, проводим прямые, параллельные оси х, и симметрично оси z откладываем на них отрезки, равные половине стороны шестиугольника (D/2). Полученные шесть точек соединяем отрезками прямых (рис.9,10).
2. Шестиугольник расположен в горизонтальной плоскости. Построение выполняем, как было рассмотрено выше , с той лишь разницей, что расстояние S
( для изометрии, рис.9) между противоположными сторонами (для фронтальной диметрии S/2, рис.10) откладываем по оси y.
3. Шестиугольник расположен в профильной плоскости. В этом случае размер D (для изометрии, рис.9), D/2- для фронтальной диметрии (рис.10) откладываем по оси y, а размер S – по оси z. В этой проекции сокращаются также стороны шестиугольника, расположенные параллельно оси y (размер D/4 – рис.10).
Построение аксонометрических проекций призм:
сначала строим проекции видимого основания (плоской фигуры), например в профильной плоскости. Через его вершины проводим прямые, параллельные оси х, и откладываем на них высоту (длину) призмы. Полученные точки соединяем отрезками прямых и обводим линии видимого контура (рис.11).
Построение аксонометрических проекций пирамид:
сначала строим проекцию основания пирамиды (плоской фигуры) и через точку О – центр тяжести полученной на плоскости фигуры – проводим вертикальную ось z. На этой оси откладываем высоту пирамиды – строим вершину. Полученные точки соединяем и обводим линии видимого контура (рис.12).
Как начертить изометрию?

Практически все, кому довелось изучать черчение и инженерную графику сталкивались с необходимостью произвести построение изометрической проекции детали. В этом уроке мы попробуем разобрать основные моменты, которые нужно знать, чтоб начертить изометрию. Уверен, что повторив указанные в этом уроке шаги, вы сможете самостоятельно выполнить и более сложное задание. В вашей детали может быть большее количество построений, но основные принципы останутся неизменными. Но при этом оговорюсь, что построение изометрии скорее всего будет вам не под силу, если вы еще не освоили построение третьего вида и построение простого разреза. Вы должны уже уметь хорошо ориентироваться в трех видах на чертеже.
Начнем с того, что определимся с направлением осей в изометрии.
На следующей схеме показано соответствие направлений, по которым откладываются размеры в изометрии по отношению к размерам на чертеже. Интересный момент: как показал опыт, этот рисунок кому-то помогает понять принцип построения, а кого-то - наоборот - ставит в тупик. Поэтому, если вас эта схема скорее смущает, нежели просветляет, не зацикливайтесь на нем и читайте дальше - вполне вероятно, что там все будет понятно.
На этом закончим вступительную часть и начнем непосредственно построение изометрической проекции детали. Возьмем для примера не очень сложную деталь. Это параллелепипед 50х60х80мм, имеющий сквозное вертикальное отверстие диаметром 20 мм и сквозное прямоугольное отверстие 50х30мм.
Начнем построение изометрии с вычерчивания верхней грани фигуры. Расчертим на требуемой нам высоте тонкими линиями оси Х и У. Из получившегося центра отложим вдоль оси Х 25 мм (половина от 50) и через эту точку проведем отрезок параллельный оси У длиной 60 мм. Отложим по оси У 30 мм (половина от 60) и через полученную точку проведем отрезок параллельный оси Х длиной 50 мм. Достроим фигуру.
Мы получили верхнюю грань фигуры. Не хватает только отверстия диаметром 20 мм. Построим это отверстие. В изометрии окружность изображается особым образом - в виде эллипса. Это связано с тем, что мы смотрим на нее под углом. Изображение окружностей на всех трех плоскостях я описал в отдельном уроке, а пока лишь скажу, что в изометрии окружности проецируются в эллипсы с размерами осей a=1,22D и b=0,71D. Эллипсы, обозначающие окружности на горизонтальных плоскостях в изометрии изображаются с осью а расположенной горизонтально, а ось b - вертикально. При этом расстояние между точками расположенными на оси Х или У равно диаметру окружности (смотри размер 20 мм).
Теперь, из трех углов нашей верхней грани начертим вниз вертикальные ребра - по 80 мм и соединим их в нижних точках. Фигура почти полностью начерчена - не хватает только прямоугольного сквозного отверстия.
Чтобы начертить его опустим вспомогательный отрезок 15 мм из центра ребра верхней грани (указан голубым цветом). Через полученную точку проводим отрезок 30 мм параллельный верхней грани (и оси Х). Из крайних точек чертим вертикальные ребра отверстия - по 50 мм. Замыкаем снизу и проводим внутреннее ребро отверстия, оно параллельно оси У.
На этом простая изометрическая проекция может считаться завершенной. Но как правило, в курсе инженерной графики выполняется изометрия с вырезом одной четверти. Чаще всего, это четверть нижняя левая на виде сверху - в этом случае получается наиболее интересный с точки зрения наблюдателя разрез (конечно же все зависит от изначальной правильности компоновки чертежа, но чаще всего это так). На нашем примере эта четверть обозначена красными линиями. Удалим ее.
Как видим из получившегося чертежа, сечения полностью повторяют контур разрезов на видах (смотри соответствие плоскостей обозначенных цифрой 1), но при этом они вычерчены параллельно изометрическим осям. Сечение же второй плоскостью повторяет разрез выполненный на виде слева (в данном примере этот вид мы не чертили).
Надеюсь, этот урок оказался полезным, и построение изометрии вам уже не кажется чем-то совершенно неведомым. Возможно, некоторые шаги придется прочитать по два, а то и по три раза, но в конечном итоге понимание должно будет прийти. Удачи вам в учебе!
Следующий шаг в черчении: Уникальный урок на тему "Как начертить диметрию детали?"
Вы можете сказать "спасибо!" автору статьи:
пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект "White Bird. Чертежи Студентам"
или запишите наш телефон и расскажите о нас своим друзьям - кто-то наверняка ищет способ выполнить чертежи
или создайте у себя на страничке или в блоге заметку про наши уроки - и кто-то еще сможет освоить черчение.
А вот это - не реклама. Это напоминание, что каждый из нас может сделать. Если хотите - это просьба. Мы действительно им нужны:
Автор комментария: светка
Дата: 2010-09-08
пипец. я ни чего не понимаю. а завтра экзамен. ((((
Мы стараемся. Правда. Но в то же время мы понимаем, что написать понятно для всех не сможем. Что поделаешь. Однако, мы стремимся оформлять статьи по начертательной геометрии, а так же статьи по инженерной графике в максимально информативном и доступном виде.
Автор комментария: гринкс
Дата: 2010-09-28
хорошо что у меня завтра не экзамен. а лишь занятие по черчению. Со второго прочтения разобрался и смог начертить изометрию своей детали, надеюсь что правильно :))) Спасибо
Автор комментария: Антон
Дата: 2010-10-14
В музыкальном колледже требуют изометрический чертёж.Я бы лучше концерт сыграл.Черчение для меня-полная тьма.
Да уж. Неисповедимы пути. Я бы тоже концерт сыграл. Но вот к сожалению черчу лучше, чем музицирую. Не отчаивайтесь! Звоните, если не разберетесь. Удачи! Антон.
Автор комментария: Елена
Дата: 2010-10-21
замечательно.всё так понятно и просто
Автор комментария: Андрес
Дата: 2010-11-28
Огромное вам спасибо, вспомнил азы=)
Автор комментария: Диана
Дата: 2011-11-25
помогите начертить изометрию
Автор комментария: Диана
Дата: 2011-11-25
Антон спасибо большое за внимание. я уже все поняла. а вы физику хорошо знаете??
Автор комментария: оля
Дата: 2012-02-17
тут хоть понятно)
Автор комментария: михаил
Дата: 2012-06-09
здравствуйте ! нужен чертеж спичечьного коробка в изометрической и диметрической проекции !
Эх, жаль ваш вопрос пришел в момент когда я был в отпуске. Изометрия спичечного коробка еще не встречалась мне в заданиях, хоть это и несложно, но все же какое-никакое разнообразие.
Автор комментария: Андрей
Дата: 2012-06-19
Блин завтра экзамен . Эту то деталь я понял как начертить, а вот смогу ли я начертить деталь из билета .
Андрей, надеюсь у вас все получилось. Но пожалуй, действительно, пришла пора сделать второй урок объясняющий построение изометрии детали приближенной к заданиям среднего уровня сложности. Жаль, что вам это уже не пригодится, но благодаря вам многим станет легче.
Автор комментария: Виктор
Дата: 2012-09-15
Спасибо, что напомнил. Я сто лет уже изометрию не чертил, хотя и работаю инженером
Автор комментария: Яна
Дата: 2012-11-18
надо ли чертить все отверстия если они одинаковые? например 5 отверстий под винты. Или достаточно обозначить их оси?
На учебные чертежи нет ГОСТов. Есть разрешенные допущения. И их количество в каждом ВУЗе свое. В вашем случае правильным будет согласовать с преподавателем, либо выполнить все отверстия.
Автор комментария: Свелана
Дата: 2012-11-19
Статья отличная,большое спасибо, всё прояснилось) Скажите, вы писали выше в коментариях, что нужно сделать изометрию детали средней сложности, не появилась ещё?
Светлана, все произошло немного по-другому. Я взял среднюю деталь, имеющую несколько окружностей в своих формах и создал по ней урок. "Как начертить диметрию?" :))) Ссылка на него находится в самом конце статьи, до комментариев. Я считаю, что он может серьезно углубить ваши знания в части понимания, как чертить аксонометрические проекции разных деталей.
Автор комментария: 9th
Дата: 2012-12-26
Офигенно. Спасибо, с первого раза всё понял.
Автор комментария: Семен
Дата: 2013-02-10
Вы маги чтоль? как вы смогли обьяснить столь бестолковому человеку такую не простую вещь?))
Семен, хотел ответить, что "нет, я только учусь!" Но это больно уж избито :) Маги? Нет. Просто мне хочется сделать жизнь вокруг меня хоть немного лучше. И если у меня есть возможность хоть немного повлиять на количество покупаемых студенческих работ, заменив уставших и разлюбивших свою работу преподавателей - я пытаюсь это сделать. Ну а вам - всего наилучшего!
Автор комментария: Александр
Дата: 2013-03-03
Ребят спасибо! Объяснено очень доходчиво, более лучшего объяснения не встречал!
Хорошо, коль так! Учитесь на здоровье!
Автор комментария: Золушка
Дата: 2013-03-05
СпасиБо! Можно двигаться дальше благодаря Вам! Появился свет в конце тоннеля!;)))
Автор комментария: Кирюха
Дата: 2013-03-17
Спасибо, все отлично написано, понятно. Особый респект автору. Еще хотелось бы узнать как показать резбу на валу в изометрической проекции.
Автор комментария: Лена
Дата: 2013-04-21
Спасибо большое. Все очень ясно изложено)
Автор комментария: Ольга
Дата: 2013-05-05
Спасибо огромное. Теперь все стало понятно, и я начертила деталь по контрольной.
Автор комментария: Серёга
Дата: 2013-06-02
Спасибо, что-то понял.
Автор комментария: MARUFJN
Дата: 2013-07-20
Автор комментария: АЙОГА
Дата: 2014-02-20
Автор комментария: Пётр
Дата: 2014-02-28
Скажите пожалуйста это в каком учебном заведении ещё есть черчение Я учусь в техническом Вузе и черчения нету
Петр, напишу в ответ следующее: МГТУ им. Н.Э Баумана, МИФИ, МАМИ, МАДИ, РХТУ, МИРЭА, МЭИ, МГУГиК, МГСУ, МАТИ, РУДН, РГУ Нефти и Газа им. Губкина, МГУПИ, МГОУ, МИСИ - вот неполный список московских ВУЗов, в которых не забыли, что такое подготовка полноценного инженера. Удачи!
Автор комментария: Татьяна
Дата: 2014-03-13
Спасибо вам большое,очень помогли,без вашего урока бы не справилась,все объяснено доходчиво и по существу,очень благодарна)))
Автор комментария: Вита
Дата: 2014-05-15
очень хорошая статья, не могли бы вы добавить изометрию шестиугольной призмы?очень надо!
Автор комментария: Марина
Дата: 2014-05-21
Большое спасибо. Знаю автокад для геологии, а черчение для меня вообще Луна, в вузе не было. Но благодаря объяснениям смогла сделать. Побольше бы таких толковых авторов. Еще раз огромное спасибо, спасли мне оценки ребенка
Автор комментария: Хама
Дата: 2014-11-04
Туфта! Размеры граней откладываются с коэффициентом 0,82 сторона не 50 мм а уже будет 0,82*50=41 хаваете инфу за должное.
ОК, расшифрую замечание внимательного читателя. В прямоугольной изометрической проекции действительные искажения по осям (по всем трем) и в самом деле равны 0,82. Но поскольку мы не оторваны от земли, и разбираемся с тем, как начертить домашнее задание, а не пишем реферат по черчению (!), то мы используем приведенные коэффициенты, равные единице. Я за 18 лет практики не встречал ни одного ВУЗа в нашей стране, где бы требовались коэффициенты 0,82. Поэтому рисуем с коэффициентом искажения по осям 1, но для энциклопедических знаний запоминаем 0,82. Не исключено, что этот вопрос когда-то будет задан в какой-нибудь телевикторине.
Автор комментария: Алексей
Дата: 2014-12-22
Начертите изометрию куба со стороной 80 мм и в каждой видимой гране впишите овал
Замечательное задание из замечательного ИКСИ? Так там же ничего сложного - просто аккуратно выполняете построения - только циркуль и только линейка.
Автор комментария: Антон
Дата: 2014-12-24
Огромное спасибо. Чудесное объяснение. Даже я понял. :)
Автор комментария: Человек
Дата: 2015-01-15
Автор комментария: Альбина
Дата: 2015-02-08
Большое спасибо, очень помогли! Сыну нужно было начертить изометрию, на уроке ничего не понял, я уже все забыла. Вместе с ним разобрались благодаря вашим объяснениям, очень доступно.
Автор комментария: Денис
Дата: 2015-03-11
Нужно ли заштриховывать ребро жесткости при сечении?
Денис, в изометрии всегда штрихую разрез вне зависимости от того, идет ли он через ребро жесткости. Так учили меня в свое время на кафедре черчения. Я готов предположить, что кто-то из преподавателей в каком-либо ВУЗе может считать иначе. В любом случае, стереть тонкие линии штриховки не составит труда. Но скорее всего стирать их не придется.
Автор комментария: Дмитрий
Дата: 2015-04-15
Очень бы хотелось видеть данный урок в pdf или doc формате. А в общем спасибо за урок!
Автор комментария: николай
Дата: 2015-11-17
Пользуйтесь на здоровье!
Автор комментария: Асхат Сабен
Дата: 2015-11-27
Я учусь в 9 классе. У нас есть урок черчения. Я №1 в классе по ЧЕРЧЕНИЯ! Я хочу стать архитектором. По этому я хочу узнать все подробности.
Вы один из очень небольшого количества современных школьников, кому довелось встретить черчение до ВУЗа. Поверьте, вам будут завидовать все ваши одногруппники на первом курсе :) А в целом - наличие цели и желание ее добиться - это здорово. Я поделился чем смог - пользуйтесь и добрым словом поминайте :)
Автор комментария: Михаил
Дата: 2015-11-30
Автор комментария: Анатолий
Дата: 2015-12-01
Это не изометрия, а аксонометрия.Есть ещё и диметрия.
Анатолий, на всякий случай попробую систематизировать ваши знания. Смотрите. Есть такая штука, называется аксонометрические проекции. Оно же аксонометрия. К ним относятся такие виды проекций как изометрия и диметрия. И еще несколько их подвидов. Но в целом - это же хорошо, что вы ищете. Главное - не перепутать ничего и правильно запомнить.
Автор комментария: Михаил
Дата: 2015-12-09
Ваш сайт первый по запросу в гугле. Что ж, совсем не зря! И разобрали как раз мой вариант. Спасибо за вашу работу!
Вот это я понимаю, вот это повезло :) А ведь деталь из головы брал! Но, как я понимаю, вы еще и суть теперь знаете, а это очень хорошо! Да, не зря я работал над оптимизацией, не зря!
Автор комментария: Сергей
Дата: 2016-01-10
Здравствуйте! А моему мнению,в чертеже с вырезанной четвертью, допущена неточность!
Сергей, приветствую! На картинке с вырезанной четвертью наверняка есть "неточности". Например нет штриховки, какие-то разноцветные линии, торчащие не по ГОСТу осевые. Но урок-то был о другом. Пусть пока остается как есть.
Автор комментария: Светлана
Дата: 2016-04-27
Хочу сказать спасибо за работу.Вы мне очень помогли .Ещё раз спасибо.
Спасибо, всё поняла (хотя черчение проходила в школе лет 40 назад))). Сейчас помогаю сыну. Предлагаю и Вам помощь: редактировать тексты перед публикацией на предмет знаков препинания (для лучшего понимания такой полезной информации!). С уважением! Успехов.
Автор комментария: Зоя
Дата: 2016-12-16
Давно уже не чертила изометрию, все забыла. Благодарю за отличный урок!
Автор комментария: Дан
Дата: 2017-01-08
Спасибо за это объяснение, лично мне аксанометрия нравится, но в отверстиях на плоскости малек туплю,блин архитектору это нужно. Спасибо вам)
Спасибо за объяснение,все четко показано
Спасибо огромное. Учителя объясняют тему не понятно, а здесь всё ясно и понятно
Спасибо большое! Хоть вспомнил правила изометрии. А то работаю авиационным инженером, завтра самолет строить, а я позабыл изометрические коэффициенты)))
такая себе хорактеристика азаметрий
Автор комментария: Андрей
Дата: 2019-07-10
Я, конечно, изучал изометрию почти 15 лет назад, но у Вас в финальном чертеже с разрезом есть ошибка. По условиям вертикальное отверстие сквозное, а на чертеже сделано не правильно. У вас это отверстие "уходит" дальше размеров самой детали. Как-то так.
Автор комментария: Андрей
Дата: 2019-07-10
Поправочка: всё правильно. Совпадают вертикальные линии задней стенки с разрезом. Изометрия такая изометрия. Пока не измерил в живую, не увидел. Конечно перспектива в этом плане более информативна.
Автор комментария: Владимир
Дата: 2020-07-31
ого, я уже забыл все что мы проходили на уроках черчения в школе, оказывается.
Автор комментария: LeOn4iK
Дата: 2020-11-15
Очень круто, мне понравилось!
Автор комментария: Александр
Дата: 2021-03-20
Сам учился в строительном, со временем что-то забывается, 30 лет прошло. Для детей и внуков приходится заглядывать. БлагоДарствую за толковое разъяснение, даже для школьников
Бро, это было 11 лет назад.
Добавьте свой комментарий:
Наша страница в ВК:
Коллеги, не тратьте время. Объявления правятся быстрее, чем индексируются. Лучше предлагайте обмен ссылками, статьями. Денег в конце концов переведите - варианты всякие можно придумать.
MorozArt Studio © 2005 • 2011 • Москва • Удаленная работа
При публикации статей с сайта активная ссылка на оригинал обязательна.

Здесь поочередно применяется способ прямоугольного треугольника для определения действительных величин отрезков, составляющих треугольник, а затем, к одному из них методом засечек строятся два других.
Используем Метод преобразования проекций для определения истиной величины треугольника на эпюре Монжа:

– Способ вращения вокруг осей перпендикулярных плоскостям проекций;

– Вращение вокруг горизонтали представляющих собой линии уровня;


представляющих собой линии уровня;
– Вращение вокруг следа или способ совмещения с плоскостью проекций;


Задача на определение натуральной величины плоской фигуры относится к разделу метрические задачи.
Ниже приведены решения одной и той же задачи вышеописанными методами.
9.6.1. Задание:определить натуральную величину треугольника ABC(рис. 9.8), а также угол наклона плоскости треугольника к плоскости П1.
1) Решение методом замены плоскостей проекций (рис. 9.9).
Плоскость треугольника спроецируется в натуральную величину в том случае, если она будет параллельна одной из плоскостей проекций. Одним преобразованием задачу решить невозможно. Она решается в два этапа: при первой замене плоскостей проекций получают плоскость треугольника ABC,перпендикулярную к новой плоскости проекций, при второй замене – получают плоскость треугольника, параллельную новой плоскости проекций.
Первый этап. Одним из условий перпендикулярности двух плоскостей является наличие прямой, принадлежащей одной из плоскостей, перпендикулярной к другой плоскости. Используя этот признак, проводят через точку А в плоскости треугольника горизонталь (h). Затем на произвольном расстоянии от горизонтальной проекции треугольника A1B1C1 проводят ось x1,4новой системы плоскостей проекций П1/П4перпендикулярно к горизонтальной проекции горизонтали h1.В новой системе треугольник ABC стал перпендикулярен к новой плоскости проекций П4.
На линиях проекционной связи в новой системе откладывают координатыzточек А, В, С с фронтальной проекции исходной системы плоскостей П1/П2.
При соединении новых проекций А4,B4, С4получают прямую линию, в которую спроецировался треугольник ABC. На этом этапе определяется угол наклона плоскости треугольника к горизонтальной плоскости проекции П1 – угол α. На чертеже это угол между осью x1,4и проекцией С4А4В4.
Второй этап. Выбираем новую плоскость проекции П5,параллельную плоскости треугольника, т.е. новую ось x4,5проводят параллельно С4А4В4на произвольном расстоянии. Получают новую систему П4/П5.Полученный треугольник А5В5С5и есть искомая натуральная величина треугольника ABC.
2) Решение методом вращения вокруг проецирующей оси(рис. 9.10).
Задача решается в два этапа. На первом этапе выполняют вращение так, чтобы плоскость треугольника ABCпреобразовалась в проецирующую плоскость, т.е. стала перпендикулярна к одной из плоскостей проекций. Для этого проводят горизонталь h (h1,h2) через точку А. (построение начинают с фронтальной проекции h2,она проходит через проекцию точки A2и проекцию точки 12 при этомh2 параллельна оси х).Далее находят горизонтальную проекцию h1 горизонтали h (через проекции A1 и 11). Через точку А проводят ось i – ось вращения треугольника так, чтобы она была перпендикулярна к П1. На фронтальной проекции через вершины А2 и В2 проводят следы горизонтальных плоскостей уровня Δ и Σв которых при вращении будут перемещаться точки АиВ. Вершина С принадлежит плоскости П1поэтому ее плоскостью вращения будет плоскость проекций П1.На горизонтальной проекции, взяв за центр вращения проекцию i1 поворачивают горизонталь А так, чтобы на плоскость П2 она спроецировалась в точку. На чертеже это выразится тем, что h’1 займет новое положение – перпендикулярно к оси х.
При этом на фронтальной проекции А2 остается неизменной, находясь на следе плоскости Σ2 и ее обозначим a2‘.
На горизонтальной проекции поворачиваем оставшиеся вершины В и С вокруг оси i так, чтобы . На фронтальной проекции вершина В перемещается по следу плоскости 2, а вершина С – по оси х. Соединив новые положения проекций всех вершин треугольника ABC, получают проекцию А’2В’2С’2,сливающуюся в линию. Плоскость треугольника ABC заняла проецирующее положение. На данном этапе, при необходимости, находят угол наклона плоскости треугольника ABC к П1 – угол α .
На втором этапе проводят ось jчерез вершинуС так, чтобы ось была фронтально проецирующая. При этом С’2 ≡ j’2, а горизонтальная проекция j’1 пройдет через проекцию С’1. Вокруг оси поворачивают треугольник так, чтобы он стал параллелен горизонтальной плоскости проекций. В данной задаче вращают точки А’2 и В’1, вокруг j2 до совмещения с осью х,при этом проекции B’1 и A’1 будут перемещаться параллельно оси хи займут новое положение В"1, и А"1 вершина С останется на месте. Соединив точки между собой, получают новое положение плоскости (оно соответствует натуральной величине треугольника ABC).
3) Решение методом плоскопараллельного перемещения (рис. 9.11).
Задача решается в два этапа. На первом этапе преобразуют чертеж так, чтобы плоскость треугольника ABC стала перпендикулярна к одной из плоскостей проекций. Для этого проводят в плоскости треугольника горизонталь h (фронтальная проекция А212║х,). Каждую вершину треугольника заключают в свою плоскость уровня, параллельную плоскости П1. В рассматриваемом примере вершина С принадлежит плоскости проекций П1, А принадлежит плоскости Σ, В — плоскости Δ.
Плоскость треугольника перемещается в пространстве до тех пор, пока горизонталь h1 треугольника не станет перпендикулярна к фронтальной плоскости проекций П2.
Для этого на свободном поле чертежа вычерчивают горизонтальную проекцию треугольника A1 ′ B1 ′ C1 ′ с условием, чтобы А111П2, а значит А1 ′ 11 ′ х. При этом вершины треугольника, перемещаясь каждая в своей плоскости, займут новое положение – (фронтальная проекция А2В2С2 заменится А’2В’2С’2).Соединив эти точки, получают новое положение треугольника ABC, спроецированного в линию, т.е. перпендикулярного к плоскости П2.
На втором этапе, чтобы получить натуральную величину треугольника ABC, его плоскость поворачивают до тех пор, пока она не будет параллельна одной из плоскостей проекций. В рассматриваемом решении фронтальную проекцию треугольника А2‘В2‘С2‘располагают на произвольном расстоянии от оси хпараллельно плоскости П1. При этом вершины А, Ви С треугольника заключают в горизонтально проецирующие плоскости θ, Т, Р. По следам этих плоскостей будут перемещаться горизонтальные проекции вершин А1‘В1‘С1‘. От нового положения фронтальной проекции А2"В2"С2" проводят линии проекционной связи до пресечения с соответствующими следами плоскостей, в которых они перемещаются (θ1,T1,P1), и получая проекции точек А1" В1" C1". Соединив эти проекции, получают треугольник ABC в натуральную величину.
4) Решение методом вращения вокруг линии уровня(рис.9.12)
Для решения задачи этим способом необходимо повернуть плоскость треугольника вокруг линии уровня, в данном случае вокруг горизонтали, до положения, параллельного горизонтальной плоскости проекции. Через точку А в плоскости треугольника ABC проводят горизонталь h, фронтальная проекция которой будет параллельна оси х. Отмечают точку 12 и находят ее горизонтальную проекцию 11. Прямая A111 является горизонтальной проекцией h1горизонтали h. Вокруг горизонтали будут вращаться точки В и С. Определяют натуральную величину радиуса вращения точки С .
Для определения натуральной величины радиуса вращения используют любой метод (в данном случае способ прямоугольного треугольника) строят прямоугольный треугольник, в котором O1C1 – один из катетов. Второй катет – разность координат Δzотрезка О2С2, взятого с фронтальной проекции. В построенном треугольнике гипотенуза O1C – натуральная величина радиуса вращения.
На продолжении перпендикуляра O1C1 откладывают |RBp.| и получают новое положение вершины С после вращения — С . Проекция вершины В получается пересечением луча C 11 и перпендикуляра к горизонтальной проекции h1 проведенного через проекцию точки В1.
Треугольник A B C есть искомая натуральная величина треугольника ABC.
5) Решение методом совмещения(рис. 9.13).
Для решения задачи методом совмещения необходимо построить следы плоскости Σ, которой принадлежит треугольник ABC. Для этого проводят в плоскости треугольника ABC фронталь f и находят горизонтальный след этой фронтали – N1. По условию задачи вершина С треугольника принадлежит горизонтальной плоскости проекций П1. Тогда горизонтальный след Σ1 плоскости Σпроводят через проекции N1 и C1. Соединив эти две точки и продлив отрезок до пересечения с осью х, находят точку схода следов Σх. Учитывая, что все фронтали плоскости параллельны ее фронтальному следу, фронтальный след Σ2 плоскости Σпроводят через точку Σхпараллельно проекции фронтали f2.
Для нахождения натуральной величины треугольника ABCнеобходимо построить совмещенное положение плоскости Σ с горизонтальной плоскостью проекций П1. Для этого через вершину Апроводят горизонталь h1. На фронтальном следе Σ2 фиксируют точку 22. Ее горизонтальная проекция – точка 21. Точка 2 вращается в плоскости, перпендикулярной к горизонтальному следу плоскости Σ. Поэтому, чтобы построить точку 2 в совмещенном положении 2 , проводят из 21перпендикуляр к горизонтальному следу Σ, а из центра Σх дугу окружности радиусом Σх22 до пересечения с направлением перпендикуляра. Соединив Σх с 2 , получают совмещенное положение фронтального следа Σ – Далее через точку 2 проводят горизонталь h всовмещенном положении. На этой горизонтали находят точку А , проведя перпендикуляр из точки A1 к горизонтальному следу Σ1.
По такой же схеме строят совмещенное положение точки В . Совмещенное положение точки С совпадает с ее горизонтальной проекцией С1 т.е. С1≡С . Соединив построенные точки, получают треугольник А В С – это и есть натуральная величина треугольника ABC.
Не нашли то, что искали? Воспользуйтесь поиском:
Метки

Натуральная величина треугольника с описанием.
Натуральная величина треугольника определяется 2 методами:
- замена плоскостей проекции;
- плоскопараллельное перемещение.
Для наглядности я использовал определенное задание и на его примере покажу как находится натуральная величина треугольника.
Алгоритм определения натуральной величины плоскости:
Замена плоскостей проекции
1.) Для построения чертежа использовал задание, расположенное снизу. Первоначально строятся точки по координат в плоскостях П1 и П2.

2.) Строится дополнительная горизонтальная линия 1 1 в верхнем изображении (проводится линия от средне расположенной точки по высоте), затем опускают дополнительные отрезки на нижнее изображение (как указано на рисунке снизу) и соединяют прямой. Эта прямая необходима для того, чтобы на ней расположить вспомогательную плоскость.

3.) Построив прямую на нижнем рисунке, чертится под углом 90 0 ось Х 1 (от точки С1 располагаем на произвольном расстоянии, но не слишком далеко). Затем отмеряются расстояния:
- от С2 до оси Х;
- от В2 до оси Х;
- от А0 до оси Х.
Полученные размеры откладываются от оси Х1 (размеры указаны разными цветами на рисунке снизу) и соединяют, далее подписываются точки.

4.) Строится еще одна дополнительная ось Х2, расположенная параллельно отрезку В 4 С 4 А 4. От точек В4,С4 и А4 проводят прямые перпендикулярные оси Х2.

5.) Отмеряются расстояния:
- от В1 до Х1;
- от С1 до Х1;
- от А1 до Х1.
Полученные результаты измерений откладываются от иси Х2 (на изображении снизу отмечены зелеными и голубым цветами).
Плоскопараллельное перемещение
7.) Откладывается отрезок на оси Х (обозначен синим цветом).


8.) Переносятся точки на текущее построение.
9.) Соединяют точки, получившиеся при переносе из плоскостей проекций. 10.) Методом вращения точки А2′, С2′ переносятся на горизонтальную прямую, а точка В2′ не меняет свое положение (относительно ее и происходило вращение).11.) Откладывается точка (располагают от оси Х на небольшом расстоянии, т.е. произвольном), относительно которой и будет откладываться плоско параллельное перемещение плоскости. 12.) От точек А2′, С2′ и В2′ опускаются прямые. Далее циркулем необходимо отмерить расстояния:
Затем эти размеры откладываются от С1′ (обозначены красным и синим цветами).
Читайте также:


