Что является технической реализацией логической переменной в компьютере
Системой логических элементов называется функционально полный набор логических элементов, объединенных общими электрическими, конструктивными и технологическими параметрами и использующих одинаковый тип межэлементных связей [ 1 ] . Системы элементов содержат элементы для выполнения логических операций, запоминающие элементы, элементы, реализующие функции узлов ЭВМ, а также элементы для усиления, восстановления и формирования сигналов стандартной формы.
Условно-графические обозначения ( УГО ) некоторых логических элементов представлены на рис.13.1.
Рис. 13.1. Условно-графические обозначения логических элементов
УГО элемента представляет собой прямоугольник , к которому слева подходят входные сигналы, а справа выходят выходные. Внутри прямоугольника ставится условное обозначение выполняемой элементом логической функции. Если значение выходного сигнала принимает инверсное значение по отношению к обозначенной внутри элемента функции, то данный выход обозначается на УГО элемента кружком (рис.13.1,в – 13.1,д). Аналогично, если активным уровнем входного сигнала является логический "0" , то данный вход обозначается кружком (вход E элемента 13.1,ж ).
Каждый логический элемент – это электронно-техническое изделие (рис.13.2). В этих схемах все транзисторы работают в ключевом режиме. Это означает, что при подаче сигнала высокого уровня на базу транзистора, его сопротивление становится пренебрежимо малым, то есть транзистор как бы "стягивается в точку". При низком потенциале на базе транзистора сопротивление между коллектором и эмиттером становится чрезвычайно большим, что фактически означает разрыв цепи.
Рис. 13.2. Схемотехническая реализация логических элементов
Рассмотрим это на примере работы инвертора (рис.13.2,а). Если сигнал X имеет высокий потенциал , то ключ , реализованный на транзисторе, замкнут, и потенциал точки Y низкий. В противном случае связь между точкой Y и "землей" разорвана, и сигнал Y имеет высокий уровень, что и обеспечивает реализацию логической функции " отрицание ".
Для элемента "И-НЕ" сигнал в точке Y будет иметь низкий уровень ( НУ ) лишь тогда, когда оба сигнала X1 и X2 имеют высокий уровень ( ВУ ). Работа этого элемента описывается таблицей 13.1.
Если принять, как это делается в наиболее распространенных сериях логических элементов, высокий уровень сигнала за логическую "1", а низкий уровень - за логический "0", то получим таблицу истинности данного элемента (таблицей 13.2).
Эта таблица соответствует логической функции "И-НЕ" .
В то же время, принимая высокий уровень сигнала за логический "0" , а низкий уровень – за логическую "1" , получим следующую таблицу истинности (табл. 13.3).
Эта таблица соответствует уже функции "ИЛИ-НЕ" .
Таким образом, кодирование сигналов в системе логических элементов может влиять на выполняемую им логическую функцию. В дальнейшем будем полагать кодировку сигналов, принятую для табл. 13.2.
Для элемента "ИЛИ-НЕ" (см. рис.13.2) сигнал в точке Y будет иметь высокий уровень лишь тогда, когда оба сигнала X1 и X2 имеют низкий уровень. Работа этого элемента описывается табл. 13.4, а его таблица истинности при сделанных предположениях о кодировке сигнала – таблицей 13.5. Эта таблица соответствует логической функции "ИЛИ-НЕ" .
Параметры элементов принято делить на статические и динамические [ 1 ] . Статические параметры инвариантны к переходным процессам и измеряются в статическом режиме. Динамические, наоборот, определяют реактивные свойства элемента и измеряются во время переходных процессов.
К статическим параметрам относятся токи, текущие по выводам схемы, и соответствующие напряжения. Отметим среди этих параметров следующие:
- ток потребления;
- напряжение источника питания;
- пороговое напряжение низкого уровня ( U 0 );
- пороговое напряжение высокого уровня ( U 1 );
- потребляемая мощность;
- нагрузочная способность;
- помехоустойчивость.
Среди многочисленных динамических параметров , характеризующих схему, выделим следующие:
- время перехода при включении ( t 10 ) (задний фронт);
- время перехода при выключении ( t 01 ) (передний фронт);
- время задержки распространения при включении ( tзд 01 );
- время задержки распространения при выключении ( tзд 10 );
- среднее время задержки распространения ( tзд ср ) – интервал времени, равный полусумме времен задержки распространения сигнала при включении и при выключении; в дальнейшем это время будем называть временем задержки элемента ( tзд ).
Проиллюстрируем некоторые статические и динамические параметры логических схем на примере работы элемента "НЕ" (см. рис. 13.2,а). Временная диаграмма входного и выходного сигналов этого элемента, на которой отмечены его статические и динамические параметры , приведена на рис. 13.3.
В цифровых устройствах техническую реализацию логических функций осуществляют логические элементы. Условные графические обозначения (УГО) наиболее распространенных элементов НЕ, И, ИЛИ, И-НЕ, ИЛИ-НЕ, исключающее ИЛИ, исключающее ИЛИ-НЕ показаны на рис.
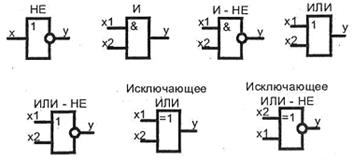
В зарубежной литературе принято логические элементы обозначать в другом виде

Практика показала нецелесообразность выпуска логических элементов, реализующих все возможные логические функции. Тем более, что с ростом числа переменных число логических функций сильно возрастает. В дальнейшем будет показано, каким образом можно реализовать любую сложную логическую функцию, используя ограниченный набор элементарных логических функций.
Тождества алгебры логики
Для математически сложных выражений устанавливается определенный порядок их расчета. В алгебре логики сложные логические выражения выполняются в следующей последовательности:
Если необходимо изменить последовательность операций, то используются скобки. Операции в скобках выполняются в первую очередь. Если одни скобки вложены в другие, то вначале выполняются операции во внутренних скобках.
Над логическими выражениями производяттождественные преобразования с использованием законов булевой алгебры.
Определение. Две функции являются эквивалентными, если они принимают одинаковые значения на одних и тех же наборах входных переменных.
Две эквивалентные функции, приравненные друг к другу, называются тождеством.
Законы булевой алгебры
1. Переместительный закон (аналогично обычной алгебре):
—для конъюнкции
От перемены мест логических слагаемых (сомножителей) их логическая сумма (логическое произведение) не меняется.
2.Сочетательный закон(аналогично обычной алгебре):
Можно различным образом группировать логические переменные при выполнении операции конъюнкции (дизъюнкции), при этом значение булевой переключательной функции не изменяется.
3. Распределительный закон
конъюнкция переменной и дизъюнкции эквивалентна дизъюнкции конъюнкций;
дизъюнкция переменной и конъюнкции равносильна конъюнкции дизъюнкций этой переменной с сомножителями.
Справедливость распределительного закона для дизъюнкции докажем с помощью таблицы истинности.
Таблица истинности распределительного закона для дизъюнкции
| a | b | c | bc | aÚbc | aÚb | aÚc | (aÚb)(aÚc) |
Значения выражения (aÚbc) и выражения (aÚb)(aÚc) совпадают для одинаковых наборов переменных. Справедливость доказана.
4. Закон инверсии (закон де Моргана).
отрицание дизъюнкции логических переменных эквивалентно конъюнкции отрицаний этих переменных;
отрицание конъюнкции переменных эквивалентно дизъюнкции отрицаний этих переменных.
Справедливость законов отрицания (де Моргана) докажем с помощью таблиц истинности.
Техническая реализация логической функции предполагает построение цифрового устройства, сигналы, на выходе которого определяются сигналами на его входах в соответствии с этой функцией.
Для построения цифрового устройства достаточно иметь элементы, реализующие три основные логические операции И, ИЛИ и НЕ. На практике также используют элементы, выполняющие другие простейшие логические операции. Такие элементы называют логическими. Их называют также логическими вентилями.
Если соединить логические элементы в соответствии со структурой выражения для логической функции, то получим цифровое устройство, реализующее заданную логическую функцию.
Логический элемент может быть реализован в виде интегральной схемы. Часто интегральная схема содержит несколько логических элементов.
На рис. 3.13 приведены примеры условных графических обозначений некоторых логических элементов, булево выражение реализуемой логической функции и их таблицы истинности.

Рисунок 3.13

Пусть имеется логическая функция вида F = x1 • x2 + x1 • x3 +
По этому выражению можно построить устройство, схема которого приведена ниже

При проектировании цифрового устройства рекомендуется поступать следующим образом:
1. По условию работы устройства определяется, что именно должно делать устройство, и уточняется алгоритм его работы.
2. Составляется таблица истинности для логической функции, реализуемой устройством.
3. Составляется логическая функция и проводится ее минимизация.
4. Разрабатывается схема проектируемого устройства.
Рассмотрим примеры проектирования некоторых цифровых устройств.
Пример 1. Необходимо спроектировать устройство включения и выключения звукового сигнала в помещении переключением одного из двух ключей, независимо от состояния другого ключа.
Требуется спроектировать логическое устройство, на выходе которого появляется сигнал логической 1 (F= 1), когда сирена включается.
При замкнутых ключах (х и у) -логические нули на входах устройства (х = 0, y = 0),
При разомкнутых ключах, логические единицы на входах устройства (х = 1, y = 1).
Учитывая сказанное, составим таблицу истинности
| № | х | y | F |
| 1 2 3 4 |
Поясним таблицу истинности:
1 строка - сирена включена (х = 0, y = 0).
2 и 3 строка –отключение сирены (выключение одного из двух ключей).
4 строка –включение сирены (выключение оставшегося включенного ключа приводит к включению сирены).
По данной таблице истинности составим логическую функцию: F = · + x · y.
Полученное логическое выражение может быть реализовано следующим образом:

Пример 2. Требуется спроектировать логическое устройство, осуществляющее передачу данных с одного из четырех входов на один выход в зависимости от комбинации сигналов на адресных входах.
Из описания следует, что проектируемое устройство имеет один выход F и четыре входа: х1, х2, х3 и x4 на которые могут подаваться логические сигналы 0 или 1, и один из входов должен подключаться к выходу в зависимости от комбинации сигналов на адресных входах.
Так как входов четыре, то, следовательно, и комбинаций на адресных шинах должно быть четыре, а для этого достаточно иметь два адресных входа А1 и А2.
С учетом этого описания можно составить следующую таблицу истинности.
| A2 | A1 | F |
| х1 х2 х3 х4 |
Из данной таблицы следует, что при нулях на обоих адресных входах к выходу устройства будет подключен первый вход данных х1.
При А1 =1, А2=0 к выходу подключен вход данных х2,
При А1= 0, А2=1 к выходу подключен вход данных х3,
При А1 =1, А2=1 к выходу подключен вход данных х4.
По данной таблице составим логическую функцию:
F = x1 + x2 A1 + x3 1 A2 + x4 A1 A2
Используя данное выражение, построим логическую схему проектируемого устройства
В электронных ЦУ наибольшее применение находят два вида цифровых сигналов — потенциальные и импульсные.
Потенциальные цифровые сигналы. Элементами потенциального цифрового сигнала являются потенциалы двух уровней. Каждый уровень потенциала на выходе некоторого ЦУ остается неизменным в течение всего времени присутствия цифры двоичного числа, уровень потенциала изменится с момента изменения цифры двоичного числа. При потенциальном способе представления двоичной переменной двум ее значениям ставится в соответствие два уровня напряжения—низкий U' и высокий U". Если высокому уровню напряжения соответствует значение логической переменной х= 1, низкому—х=0, то говорят, что устройство работает с положительной логикой (рис. 2, а). Если высокому уровню напряжения ставится в соответствие значение логической переменной х=0, а низкому х=1, то устройство работает с отрицательной логикой (рис. 2, б).
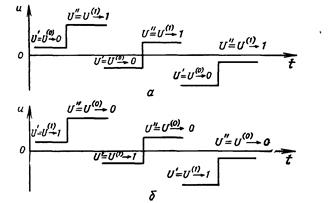
Рис. 2 Уровни потенциального цифрового сигнала
Например, имеем двоичное число 100110011. На рис. 3 изображен потенциальный цифровой сигнал, представляющий это число, написанное сверху: высокий потенциал отображен 1, а низкий—0. ЦА, работающие с такими сигналами, называются потенциальными.
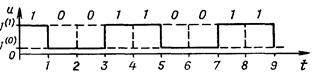
Рис. 3 Потенциальной цифровой сигнал
Импульсные цифровые сигналы. При использовании импульсных цифровых сигналов значение логической переменной определяется на интервале действия тактового импульса, который подается на специальный вход ЦА. Логической единице ставится в соответствие обычно появление импульса, логическому нулю—отсутствие его. ЦА, работающие с такими сигналами, называются импульсными (рис. 4).
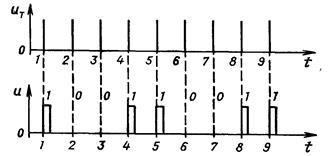
Рис. 4 Импульсный цифровой сигнал
В настоящее время в связи с развитием микроэлектроники импульсные ЦА находят ограниченное применение.
В некоторых ЦА часть логических переменных отображается потенциальными цифровыми сигналами, а другая часть — импульсными. Такие ЦА называются потенциально-импульсными. При этом потенциалы (рис. 3) и импульсы (рис. 4), соответствующие разрядам числа, передаются по одной линии и обрабатываются ЦА последовательно. Время обработки одного слова определяется произведением времени обработки одной цифры на количество разрядов слова.
Таким образом, обработка цифровой информации в ЦС производится электронными схемами – цифровыми устройствами. При этом в электронных ЦУ наибольшее применение находят два вида цифровых сигналов — потенциальные и импульсные.
1. В современных ЦС применяются в основном двоичные модифицированные коды
2. Обработка цифровой информации в ЦС производится электронными схемами – цифровыми устройствами.
3. Функция логических переменных, принимающая два значения (0 или 1), называется логической функцией (переключательной функцией).
4. В электронных ЦУ наибольшее применение находят два вида цифровых сигналов — потенциальные и импульсные.
Читайте также:


