Что такое компьютерные алгоритмы

Обновлено: 15.01.2025

Для решения большинства задач существует множество готовых программ. Но для того чтобы лучше понимать все происходящее с компьютером и уверенно принимать правильные решения, рядовому пользователю необходимо обладать определенной компьютерной грамотностью.

Следует отметить, что большинство редакторов (например, Microsoft Office Word, Excel) имеют встроенные средства программирования, освоив которые можно значительно расширить свои возможности.

Появление алгоритмов связывают с зарождением математики. Более 1000 лет назад (в 825 году) ученый из города Хорезма Абдулла (или Абу Джафар) Мухаммед бен Муса аль-Хорезми создал книгу по математике, в которой описал способы выполнения арифметических действий над многозначными числами. Само слово алгоритм возникло в Европе после перевода на латынь книги этого математика.

Алгоритм – описание последовательности действий (план), строгое исполнение которых приводит к решению поставленной задачи за конечное число шагов.

Вы постоянно сталкиваетесь с этим понятием в различных сферах деятельности человека (кулинарные книги, инструкции по использованию различных приборов, правила решения математических задач. ). Обычно мы выполняем привычные действия не задумываясь, механически. Например, вы хорошо знаете, как открывать ключом дверь. Однако, чтобы научить этому малыша, придется четко разъяснить и сами эти действия и порядок их выполнения:

1. Достать ключ из кармана.

2. Вставить ключ в замочную скважину.

3. Повернуть ключ два раза против часовой стрелки.

Если вы внимательно оглянитесь вокруг, то обнаружите множество алгоритмов которые мы с вами постоянно выполняем. Мир алгоритмов очень разнообразен. Несмотря на это, удается выделить общие свойства, которыми обладает любой алгоритм.

Свойства алгоритмов:

1. Дискретность (алгоритм должен состоять из конкретных действий, следующих в определенном порядке);

2. Детерминированность (любое действие должно быть строго и недвусмысленно определено в каждом случае);

3. Конечность (каждое действие и алгоритм в целом должны иметь возможность завершения);

4. Массовость (один и тот же алгоритм можно использовать с разными исходными данными);

5. Результативность (отсутствие ошибок, алгоритм должен приводить к правильному результату для всех допустимых входных значениях).

Виды алгоритмов:

1. Линейный алгоритм (описание действий, которые выполняются однократно в заданном порядке);

2. Циклический алгоритм (описание действий, которые должны повторятся указанное число раз или пока не выполнено задание);

3. Разветвляющий алгоритм (алгоритм, в котором в зависимости от условия выполняется либо одна, либо другая последовательность действий)

Для более наглядного представления алгоритма широко используется графическая форма - блок-схема, которая составляется из стандартных графических объектов.

Каждый программист знает о важности использования алгоритмов. В этой статье мы поговорим о том, что такое алгоритм и какими характеристиками он обладает. А самое главное — составим список алгоритмов, которые широко применяются в программировании на разных языках и, стало быть, будут полезны для любого программиста.

Algorithm — что это?

Если говорить неофициально, то алгоритмом можно назвать любую корректно определённую вычислительную процедуру, когда на вход подаётся какая-нибудь величина либо набор величин, а результатом выполнения этой процедуры становится выходная величина либо набор значений. Можно сказать, что алгоритм — это некая последовательность действий (вычислительных шагов), благодаря чему происходит преобразование входных данных в выходные данные.

Также нужно понимать, что алгоритм как последовательность шагов позволяет решать конкретную задачу и должен: 1. Работать за конечный объём времени. Если алгоритм не способен разобраться с проблемой за конечное количество времени, можно сказать, что он бесполезен. 2. Иметь чётко определённые инструкции, порядок. Любой шаг должен точно определяться. Его инструкции должны быть однозначны для любой последовательности шагов. 3. Быть пригодным к использованию. Алгоритм должен быть способен решить проблему, для устранения которой его создавали.

Если интересуют подробности, вот отдельные статьи про свойства алгоритма, а вот про способы представления и записи алгоритма.

Сегодня алгоритмы используются при обработке данных как в информатике и программировании, так и в математике. Кстати, наиболее ранними математическими алгоритмами называют разложение на простые множители и извлечение квадратного корня — их использовали в древнем Вавилоне ещё в 1600 г. до н. э. Но мы не будем уходить далеко в прошлое, а рассмотрим, как и обещали, основные алгоритмы программирования на сегодняшний день.

Алгоритмы сортировки (пирамидальная, быстрая, слиянием)

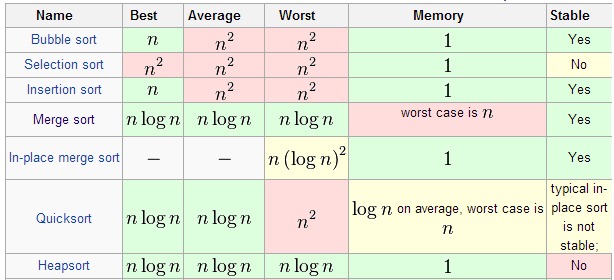
Какой алгоритм сортировки считают лучшим? Здесь нет однозначного ответа, ведь всё зависит от ваших предпочтений и поставленных перед вами задач. Рассмотрим несколько основных: 1. Сортировка слиянием. Важнейший на сегодня, базируется на принципе сравнения элементов и задействует подход «разделяй и властвуй», позволяя более эффективно решать проблемы, которые когда-то решались за время O (n^2). Сортировка слиянием была изобретена математиком Джоном фон Нейманом в далёком 1945 году. 2. Быстрая сортировка. Это уже другой подход и несколько иная процедура. Тут алгоритм базируется, как на in-place разделении, так и на принципе «разделяй и властвуй». Однако эта сортировка нестабильна, что и является её проблемой. Зато алгоритм эффективен при сортировке массивов в оперативной памяти. 3. Пирамидальная сортировка. Алгоритм in-place который использует приоритетную очередь (за счёт этой очереди сокращается время поиска данных).

Некоторые пользователи утверждают, что именно благодаря алгоритмам сортировки у нас сегодня есть искусственный интеллект, глубинный анализ данных и даже интернет.

Преобразование Фурье. Быстрое преобразование Фурье

Электронно-вычислительные устройства используют алгоритмы для функционирования, в том числе и алгоритм преобразования Фурье. И телефон, и смартфон, и компьютер, и маршрутизатор, и интернет — всё это не может работать без алгоритмов для функционирования, запомните это.

Dijkstra's algorithm

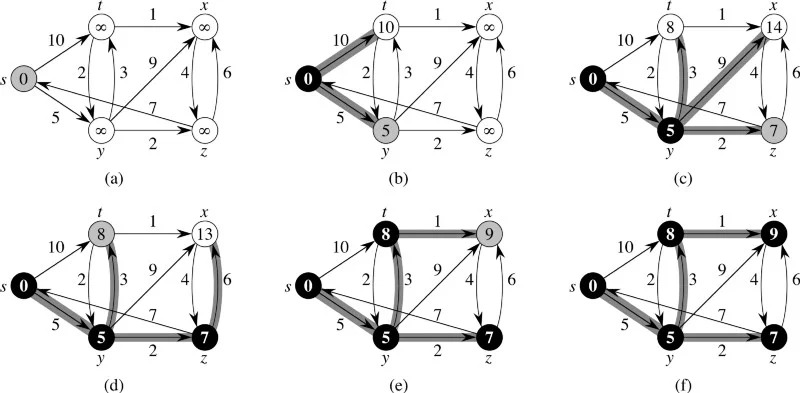
Без этого алгоритма, опять же, не сможет эффективно работать тот же интернет. С его помощью решаются задачи, в которых проблема представляется в виде графа, обеспечивающего поиск наикратчайшего пути между 2-мя узлами. Даже сегодня, когда у нас есть решения и получше, программисты по-прежнему используют поиск кратчайшего пути, если речь идёт о системах, требующих повышенной стабильности.

Algorithm RSA

Пришёл к нам из криптографии и сделал криптографию доступной всем, предопределив её будущее. Вообще, он служит для решения простой задачи с неочевидным решением и позволяет делиться открытыми ключами между конечными пользователями и независимыми платформами таким образом, чтобы можно было применять шифрование.

Алгоритм безопасного хэширования

Ну, это не совсем algorithm. Скорее, его можно назвать семейством криптографических хэш-функций (SHA-1, SHA-2 и т.д.), которые разработаны в США и имеют важнейшее значение для всего мира. Антивирусы, электронная почта, магазины приложений, браузеры и т. п. — во всём этом используются алгоритмы безопасного хэширования (на деле хэш является результатом их работы). Алгоритм служит для определения, удалось ли пользователю загрузить то, что хотелось, а также не подверглись ли вы фишингу или атаке «человек посередине».

Анализ связей

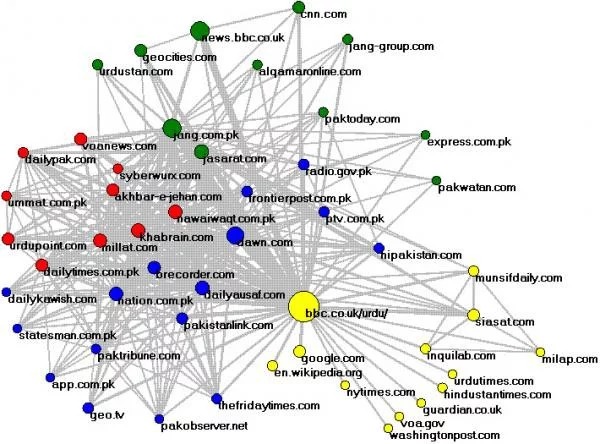
Идея анализа связей проста. К примеру, вы легко сможете представить график в виде матрицы, что сведёт задачу к проблеме уровня собственной значимости каждого узла. Данный подход к структуре графа позволит оценить относительную важность каждого объекта, который включён в систему.

Algorithm был создан в далёком 1976 году и используется сегодня при ранжировании страниц в процессе поиска в Google, при генерации ленты новостей, при составлении списка возможных друзей на Facebook, при работе с контактами в LinkedIn и во многих других случаях. Любой из перечисленных сервисов работает с различными объектами и параметрами и объектами, однако сама математика по сути не меняется.

Пропорционально-интегрально-дифференцирующий algorithm

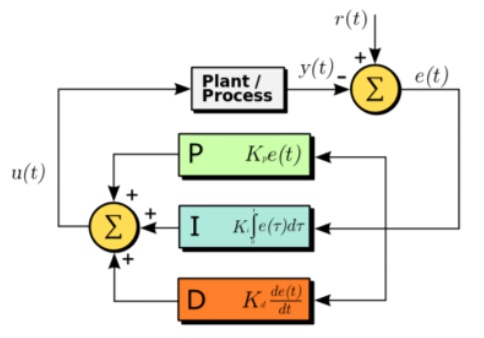
Пользовались ли вы автомобилем, самолётом, сотовой связью? Видели ли вы робота в работе? Во всех этих случаях вы можете сказать, что видели данный algorithm в действии.

Его обычно применяет замкнутый механизм обратной связи для контура управления. Это необходимо для минимизации ошибки между реальным выходным сигналом и желаемым выходным сигналом. Задействуется там, где необходимо создать систему для обработки сигнала либо для управления гидравлическими, механическими и тепловыми механизмами автоматизированного типа.

Сжатие данных

Сложно сказать, какой algorithm для сжатия наиболее важен, ведь в зависимости от поставленных задач он может меняться от zip до mp3 либо от JPEG до MPEG-2. Но эти алгоритмы важны почти для всех сфер деятельности.

Алгоритм сжатия — это не только очередной заархивированный документ. Он позволяет выполнять сжатие данных на веб-странице при их загрузке на компьютер. Или задействуется в базах данных, видео, музыке, облачных вычислениях. По сути алгоритмы сжатия данных делают системы дешевле и эффективнее.

Алгоритм генерации случайных чисел

На самом деле не существует «настоящего» генератора случайных чисел, и мы уже об этом говорили. Зато у нас существуют генераторы псевдослучайных чисел, которые прекрасно делают свою работу. Они имеют расширенную вариативность использования: программные приложения в программировании, криптография, алгоритмы хэширования, видеоигры, искусственный интеллект, тесты при разработке программ и т. д.

Алгоритмы в науке и технике

Роль алгоритмических последовательностей в современной науке и технике очень велика. Их без преувеличения считают богатством науки и техники, которое накапливалось десятилетиями. Можно вспомнить пресловутую машину Тьюринга и не только.

Однако на деле наибольшее значение имеют algorithms, которые накоплены в математике, ведь именно математика пронизывает иные технические науки и делает их более структурированными. Замечено, что если удается получить алгоритмическую последовательность данных, позволяющую решить конкретную задачу, то можно создать соответствующую машину, что если удалось получить алгоритм решения какой-нибудь задачи, то можно создать машину, стало быть, автоматизировать решение этой задачи. А автоматизация важна не только в IT-сфере, но и в промышленности, технике, науке, медицине и многих других отраслях.

С этой точки зрения суть алгоритмов можно выразить иначе, то есть они являются: - формой изложения научных данных, результатов исследований и анализа; - реальным руководством к действию по решению ранее изученных проблем; - средством экономии времени и умственной работы; - важным и нужным этапом по автоматизации; - инструментом исследования новых проблем (особенно в математике).

Да, algorithms -- важная часть как всей науки, так и локальной обработки исходных данных, но эта часть не исчерпывает содержание самой науки. Не менее важны понятия и определения, которые входят в эту науку, установленные факты (доказанные теоремы), выработанные подходы к изучаемым явлениям и объектам.

Раз уж вспомнили математику, скажем, что большой вклад в развитие алгоритмов здесь внесли советские (российские) ученые. К примеру, хорошо известен так называемый алгоритм четырех русских -- метод алгоритмического ускорения с использованием булевых матриц. Он был создан четырьмя русскими учеными В. Л. Арлазаровым, Э. А. Диницем, М. А. Кронродом и И. А. Фараджевым в 1970 г. в Москве. Также упоминания заслуживает один известный метод русского ученого Анатолия Карацубы -- созданный им алгори тм служит для быстрого умножения. И так далее.

Говорить на эту тему можно очень долго. Если же вы хотите освоить нужные алгоритмические последовательности на практике и в контексте программирования, добро пожаловать на специальный курс в OTUS!

Каждый программист знает о важности использования алгоритмов . В этой статье мы поговорим о том, что такое алгоритм и какими характеристиками он обладает. А самое главное — составим список алгоритмов , которые широко применяются в программировании и, стало быть, будут полезны для программиста.

Алгоритм — что это?

Если говорить неофициально, то алгоритмом можно назвать любую корректно определённую вычислительную процедуру , когда на вход подаётся какая-нибудь величина либо набор величин, а результатом выполнения становится выходная величина либо набор значений. Можно сказать, что алгоритм — это некая последовательность вычислительных шагов , благодаря чему происходит преобразование входных данных в выходные.

Также нужно понимать, что алгоритм как последовательность шагов позволяет решать конкретную задачу и должен:

1. Работать за конечный объём времени. Если алгоритм не способен разобраться с проблемой за конечное количество времени, можно сказать, что этот алгоритм бесполезен.

2. Иметь чётко определённые инструкции. Любой шаг алгоритма должен точно определяться . При этом его инструкции должны быть однозначны для любого случая.

3. Быть пригоден к использованию. Речь идёт о том, что алгоритм должен быть способен решить проблему , для устранения которой его создавали.

Сегодня алгоритмы используются как в информатике и программировании, так и в математике. Кстати, наиболее ранними математическими алгоритмами называют разложение на простые множители и извлечение квадратного корня — их использовали в древнем Вавилоне ещё в 1600 г. до н. э. Но мы не будем уходить далеко в прошлое, а рассмотрим, как и обещали, основные алгоритмы программирования на сегодняшний день.

Алгоритмы сортировки (пирамидальная, быстрая, слиянием)

Какой алгоритм сортировки считают лучшим? Здесь нет однозначного ответа, ведь всё зависит от ваших предпочтений и поставленных перед вами задач. Рассмотрим каждый из алгоритмов:

1. Сортировка слиянием . Важнейший на сегодня алгоритм. Базируется на принципе сравнения элементов и задействует подход «разделяй и властвуй», позволяя более эффективно решать проблемы, которые когда-то решались за время O (n^2). Сортировка слиянием была изобретена математиком Джоном фон Нейманом в далёком 1945 году.

2. Быстрая сортировка . Это уже другой подход к сортировке. Тут алгоритм базируется, как на in-place разделении, так и на принципе «разделяй и властвуй». Однако эта сортировка нестабильна, что и является её проблемой. Зато алгоритм эффективен при сортировке массивов в оперативной памяти.

3. Пирамидальная сортировка . Алгоритм in-place который использует приоритетную очередь (за счёт этой очереди сокращается время поиска данных).

Считается, что вышеописанные алгоритмы лучше, если сравнивать их с другими, например, сортировкой пузырьком . Можно сказать, что именно благодаря алгоритмам сортировки у нас сегодня есть искусственный интеллект, глубинный анализ данных и даже интернет .

Преобразование Фурье. Быстрое преобразование Фурье

Электронно-вычислительные устройства используют алгоритмы для функционирования, в том числе и алгоритм преобразования Фурье . И телефон, и смартфон, и компьютер, и маршрутизатор, и интернет — всё это не может работать без алгоритмов для функционирования, запомните это.

Алгоритм Дейкстры

Без этого алгоритма, опять же, не сможет эффективно работать тот же интернет. С его помощью решаются задачи, в которых проблема представляется в виде графа, обеспечивающего поиск наикратчайшего пути между 2-мя узлами. Даже сегодня, когда у нас есть решения и получше, программисты по-прежнему используют поиск кратчайшего пути , если речь идёт о системах, требующих повышенной стабильности.

Алгоритм RSA

Это алгоритм пришёл к нам из криптографии . Он сделал криптографию доступной всем, предопределив её будущее. Вообще, RSA-алгоритм сделан для решения простой задачи с неочевидным решением . Он позволяет делиться открытыми ключами между конечными пользователями и независимыми платформами таким образом, чтобы можно было применять шифрование.

Алгоритм безопасного хэширования

Ну, это не совсем алгоритм. Скорее, его можно назвать семейством криптографических хэш-функций (SHA-1, SHA-2 и т.д.), которые разработаны в США и имеют важнейшее значение для всего мира. Антивирусы, электронная почта, магазины приложений, браузеры и т. п. — во всём этом используются алгоритмы безопасного хэширования (на деле хэш является результатом их работы). Алгоритм нужен для определения, удалось ли вам загрузить то, что хотели, а также не подверглись ли вы фишингу или атаке «человек посередине».

Анализ связей

Идея алгоритма анализа связей проста. Например, вы легко сможете представить график в виде матрицы, что сведёт задачу к проблеме уровня собственной значимости каждого узла. Данный подход к структуре графа позволит оценить относительную важность каждого объекта, который включён в систему.

Алгоритм был создан в далёком 1976 году и используется сегодня при ранжировании страниц в процессе поиска в Google, при генерации ленты новостей, при составлении списка возможных друзей на Facebook, при работе с контактами в LinkedIn и во многих других случаях. Любой из перечисленных сервисов работает с различными объектами и параметрами и объектами, однако сама математика по сути не меняется.

Пропорционально-интегрально-дифференцирующий алгоритм

Пользовались ли вы автомобилем, самолётом, сотовой связью? Видели ли вы робота в работе? Во всех этих случаях вы можете сказать, что видели данный алгоритм в действии.

Пропорционально-интегрально-дифференцирующий алгоритм обычно применяет замкнутый механизм обратной связи для контура управления. Это необходимо для минимизации ошибки между реальным выходным сигналом и желаемым выходным сигналом. Алгоритм задействуется там, где необходимо создать систему для обработки сигнала либо для управления гидравлическими, механическими и тепловыми механизмами автоматизированного типа.

Алгоритмы сжатия данных

Сложно сказать, какой алгоритм для сжатия наиболее важен, ведь в зависимости от поставленных задач он может меняться от zip до mp3 либо от JPEG до MPEG-2. Но эти алгоритмы важны почти для всех сфер деятельности.

Алгоритм генерации случайных чисел

На самом деле не существует «настоящего» генератора случайных чисел, и мы уже об этом говорили . Зато у нас существуют генераторы псевдослучайных чисел , которые прекрасно с этим справляются. Они имеют расширенную вариативность использования: программные приложения в программировании, криптография, алгоритмы хэширования, видеоигры, искусственный интеллект, тесты при разработке программ и т. д.

Алгоритмы появились вместе с математикой, а первые упоминания о них встречаются в книге математика Мухаммеда бен Мусы аль-Хорезми из города Хорезма. Он описал методы выполнения различных действий с многозначными числами еще в 825 году. Само слово «алгоритм» появилось после того, как книгу ученого перевели на латинский язык в Египте.

Современное определение алгоритма в информатике — это описание действий, последовательное выполнение которых позволяет решить поставленную задачу за конкретное количество шагов.

С этим человек сталкивается каждый день, когда читает рецепты в кулинарных книгах, инструкции к различной технике, правила решения заданий. Но обычно все эти действия выполняются автоматически, без их анализа. Родители сталкиваются с этим понятием, когда объясняют детям, как открыть двери ключом или почистить зубы. Алгоритмов в окружающем мире множество, но есть общие признаки для всех их видов.

Свойства и виды

Для изучения понятия нужно разобраться в свойствах алгоритма в информатике. Их существует несколько:

дискретность;
детерминированность или определенность;
понятность;
завершаемость или конечность;
массовость или универсальность;
результативность.

Согласно свойству дискретности, алгоритмы должны описывать весь процесс решения задания в виде выполнения простых шагов. При этом на пункты отводится определенное количество времени. Каждый шаг должен определяться состоянием системы, то есть при одних и тех же исходных данных результат не меняется. Но есть и вероятностные алгоритмы, где пункты зависят от системы и случайно генерируемых чисел. В этой ситуации понятие становится подвидом обычного.

Понятность заключается в том, что команды алгоритма должны быть доступны конкретному исполнителю и входить в его личную систему. В ходе работы математическая функция при правильно заданных исходных данных выдает результат за определенное количество шагов. Иногда процедура может не завершиться, но вероятность таких случаев стремится к нулю.

Универсальность или массовость позволяет использовать алгоритм с разными наборами начальных данных. Последнее свойство обеспечивает его завершение в виде определенного числа — результата.

У каждого алгоритма есть свои начальные условия, цели и пути решения задачи. Существует большая разница между вычислительными и интерактивными видами. Происхождение первых связано с опытами ученого Тьюринга, они могут преобразовать входные данные в выходные. Вторые предназначены для связи с объектом управления, они работают только под внешним воздействием. Ученые выделяют несколько видов алгоритмов в информатике:

детерминированные или жесткие;
гибкие;
линейные;
разветвляющиеся;
циклические;
вспомогательные;
структурные блок-схемы.

Жесткие еще называются механическими, так как чаще всего они используются для работы двигателя или машины. Они задают действия в единственно верной последовательности, что приводит к искомому или требуемому результату при условии выполнения процессов, для которых они и разработаны.

Гибкие алгоритмы делятся на эвристические и вероятностные. Первые используются при различных умственных выводах без строгих аргументов, а вторые дают возможность получить один результат несколькими способами.

Линейный тип — это набор команд, которые выполняются в строгой последовательности. Разветвляющийся включает хотя бы одно условие и при проверке дает разделение на несколько блоков. Появляются альтернативные ветвления программы.

В циклических видах несколько раз повторяются одни и те же действия, при этом меняются исходные данные. Сюда относятся переборы вариантов и бо́льшая часть способов расчета. Циклом в этом случае называют последовательность команд, которые нужно выполнить множество раз для достижения требуемого результата.

Подчиненный или вспомогательный вид является ранее разработанным алгоритмом для быстрого решения задачи. Он необходим для сокращения записи, если в структуре есть одинаковые команды. Схемами называются графические изображения с помощью блоков и соединяющих их прямых линий. Их используют перед программированием в качестве наглядных примеров, поскольку зрительное восприятие позволяет быстрее осмыслить процесс обработки информации и выявить возможные ошибки. В блоках отображаются исходные данные, которые вносятся в компьютер для вычислений.

Способы записи

Алгоритмы записываются несколькими методами. В информатике используется всего три:

словесно-формульный;
графический;
программный.

В первом случае алгоритм записывается простым языком — словами и математическими формулами, что необходимо для понимания его теории. Здесь учитываются исходные данные, действия с ними и условия получения результата. Второй тип записи — компьютерное описание. Для этого применяются языки программирования и сами программы — форсы представления расчетов для их выполнения машиной.

Графическое описание состоит из связанных между собой географических фигур. Основные элементы блок-схем:

прямоугольники;
эллипсы;
ромбы;
шестиугольники;
стрелки;
пунктирные линии;
соединительные фигуры.

В прямоугольниках записывают процессы, они указывают на выполнение операций, которые изменяют форму или значение данных. Ромбы содержат способы решения, здесь выбирается следующее направление в зависимости от поставленных условий. Модификации могут передаваться в шестиугольниках, где записываются операции, меняющие команды.

В блок-схемах можно выделить ручной ввод и предопределенные процессы. Первая фигура позволяет исполнителю ввести данные во время работы алгоритма через устройства, подключенные к компьютеру. Второе понятие заключается в использовании заранее записанных алгоритмов.

Графическое изображение содержит блоки документов и дисплеев. Оператор может вводить данные с бумаги и выводить их на нее, а также с помощью устройств, которые воспроизводят информацию на экране (проекторы для интерактивных досок, подключенные к компьютерам планшеты и ноутбуки).

Линии и соединительные фигуры указывают на связи между разными блоками и их последовательность. В схеме есть блоки начала и конца алгоритма, его прерывания, которое может произойти из-за сбоев в программе. Можно также указывать комментарии и пояснения исполнителя, для этого есть отдельные фигуры.

Правила создания

Существует несколько правил создания алгоритмов. Если их соблюдать, то в ходе работы всегда будет верный результат. Форма должна быть настолько простой, чтобы ее понял тот, кто занимается ее разработкой. Также не должно возникнуть проблем с чтением у того, кто будет выполнять описанные действия.

Объект, который проводит расчеты в алгоритме, называется исполнителем. Идеальными считаются роботы, компьютеры и другие машины. Они работают с программами, то есть схемами, написанными определенным языком программирования.

Разобраться с действиями помогут простые примеры алгоритмов по информатике. Когда есть ряд чисел от 1 до 100 и необходимо найти из них простые, то выбираются те, что делятся на единицу и себя. В этом случае используется циклическая структура:

сначала нужно взять число 1;
проверить, меньше ли оно, чем 100;
если да, то узнать, простое ли оно;
при выполнении условия записать;
перейти к числу 2;
повторить операцию.

Такие действия проводят со всеми числами. При этом первые четыре шага будут постоянно повторяться. Если попадается число, не являющееся простым (4, 6, 8 и т. д. ), то его нужно просто пропустить. Алгоритм в этом случае обладает предусловиями, то есть проверки происходят в начале цикла.

Анализ работы

Распространение информационных технологий привело к увеличению риска сбоев в работе программ. Предотвратить появление ошибок в алгоритмах можно с помощью доказательства их корректности математическими средствами. Такой анализ называется формальным методом, он предусматривает использование специального набора инструментов.

Гипотеза Ричарда Мейса утверждает, что избежать ошибок легче, чем их устранить. Благодаря доказательству корректности программ можно выявить их свойства, применяемые ко всем видам входных данных. Само понятие делится на две разновидности — частичную и полную. При первом типе корректности алгоритм дает правильный результат только для тех случаев, когда он завершается. Во втором случае программа завершает работу корректно для всего диапазона данных.

Исполнители во время проверки сравнивают выдаваемые данные со спецификой требуемого результата. Для доказательства корректности используются предусловия и постусловия. Первые должны выполняться перед включением программы, вторые — после завершения ее работы. Формальные методы успешно применяются для многих задач: верификации программ и микропроцессоров, разработки искусственного интеллекта, электронных схем и автоматических систем для железной дороги, спецификации стандартов.

Для выполнения алгоритма нужно только конкретное количество шагов, но на практике для этого потребуется много времени. В связи с этим введено понятие сложности. Она бывает временной, вычислительной и связанной с размерами алгоритма. Для увеличения эффективности используются быстрые программы, которые появились еще в 50-х годах прошлого века.

Роль алгоритмов в программировании. В настоящее время наибольшей популярностью пользуются системы объектно-ориентированного программирования (Visual Basic, Delphi). Разработка программы с помощью такой системы программирования состоит из двух этапов: 1) создание в визуальном режиме элементов графического интерфейса программы; 2) разработка программного кода. Такой подход существенно облегчает создание программ, так как разработка графического интерфейса вручную (в процедурных языках) сложный и трудоёмкий процесс.

Первый шаг к пониманию важности изучения и знания алгоритмов это дать точное определение тому, что понимается под алгоритмом. Алгоритм в программировании- это понятная и точная последовательность действий , записанных на языке программирования. Согласно популярной книге Алгоритмы: построение и анализ (Кормен, Лейзерсон, Ривест, Штайн)"алгоритм (algorithm) - это любая корректно определенная вычислительная процедура, на вход (input) которой подается некоторая величина или набор величин, и результатом выполнения которой является выходная (output) величина или набор значений". Другими словами, алгоритмы похожи на дорожные карты для достижения четко определенной цели. Код, для вычисления членов последовательности Фибоначчи - это реализация конкретного алгоритма. Даже простая функция сложения двух чисел является алгоритмом, хотя и простым.

Для создания алгоритма (программы) необходимо знать:

полный набор исходных данных задачи (начальное состояние объекта);

цель создания алгоритма (конечное состояние объекта);

систему команд исполнителя (то есть набор команд, которые исполнитель понимает и может выполнить).

Полученный алгоритм (программа) должен обладать следующим набором свойств:

дискретность (алгоритм разбит на отдельные шаги - команды);

однозначность (каждая команда определяет единственно возможное действие исполнителя);

понятность (все команды алгоритма входят в систему команд исполнителя);

результативность (исполнитель должен решить задачу за конечное число шагов).

Большая часть алгоритмов обладает также свойством массовости (с помощью одного и того же алгоритма можно решать множество однотипных задач).

Некоторые алгоритмы, к примеру, для вычисления последовательности Фибоначчи, являются интуитивно понятными и относятся к врожденным навыкам логического мышления и решения задач. Тем не менее, большинству из нас будет не лишним изучить и сложные алгоритмы, чтобы в будущем можно было использовать их в качестве строительных блоков для более эффективного решения логических задач. В действительности можно удивиться, узнав как много сложных алгоритмов используется людьми при проверке электронной почты или прослушивании музыки. В этой статье представлены некоторые основные идеи анализа алгоритмов с практическими примерами, иллюстрирующими важность изучения алгоритмов.

Язык программирования - набор правил записи алгоритмических структур и данных.

Анализ времени выполнения алгоритма

Одним из наиболее важных аспектов алгоритма является его скорость. Часто бывает легко придумать алгоритм решающий задачу, но если алгоритм слишком медленный, то он возвращается на доработку. Поскольку точная скорость алгоритма зависит от того где запускается алгоритм, а также деталей реализации, компьютерные специалисты обычно говорят о времени выполнения относительно входных данных. Например, если вход состоит из N целых чисел, то алгоритм может иметь время выполнения пропорциональное N 2 , что представляется как O(N 2 ). Это означает, что если вы запустите реализацию алгоритма на компьютере с входом размером в N, то это займет C*N 2 секунд, где C-некоторая константа, которая не меняется с изменением размера входа.

Тем не менее, время выполнения многих сложных алгоритмов зависит не только от размера входных данных, но и от множества других факторов. Например, алгоритм сортировки множества целых чисел может работать намного быстрее, если это множество уже отсортировано. Принято говорить о наихудшем случае выполнения, и среднем случае выполнения. Наихудшее время выполнения - это максимальное время работы алгоритма при самом "плохом" из всех возможных входов. Средний случай выполнения - это среднее время работы алгоритма на всех возможных входах. Из этих двух типов времени выполнения, легче всего рассуждать о наихудшем случае и поэтому его используют чаще в качестве эталона для заданного алгоритма. Процесс определения наихудшего и среднего случая времени выполнения алгоритма может быть достаточно сложным, т.к. обычно невозможно запустить алгоритм для всех возможных входов.

Выше отмечалось, что один и тот же алгоритм может быть записан по-разному. Можно записывать алгоритм естественным языком. В таком виде мы используем рецепты, инструкции и т.п. Для записи алгоритмов, предназначенных формальным исполнителям, разработаны специальные языки программирования . Любой алгоритм можно описать графически в виде блок-схемы . Для этого разработана специальная система обозначений:

Начало и конец алгоритма

Ввод и вывод данных.

Вывод данных иногда обозначают иначе:

В вычислительных алгоритмах так обозначают присваивание

Развилка - компонент, необходимый для реализации ветвлений и циклов

Начало цикла с параметром

В программировании - процедуры или подпрограммы

Переходы между блоками

Приведем пример описания алгоритма суммирования двух величин в виде блок-схемы:

Такой способ описания алгоритм наиболее нагляден и понятен человеку. Поэтому, алгоритмы формальных исполнителей обычно разрабатывают сначала в виде блок-схемы, и только затем создают программу на одном из языков программирования.

Сортировка

Сортировка является хорошим примером алгоритма, который часто используется программистами. Самый простой способ отсортировать группу элементов это начать с удаления наименьшего элемента из группы, и поставить его первым. Затем удаляется второй по величине элемент и ставится вторым и т.д. К сожалению, время работы этого алгоритма составляет O(N 2 ), а это означает, что потребуется количество времени пропорциональное количеству элементов в квадрате. Если бы нам пришлось сортировать млрд. элементов, то этот алгоритмы бы потребовал 10 18 операций. Если считать что обычные настольные ПК делают примерно 10 9 операций в секунду, то потребуются годы чтобы закончить сортировку этого млрд. элементов.

К счастью существует ряд более совершенных алгоритмов, например, быстрая сортировка (quicksort), пирамидальная сортировка (heapsort) и сортировка слияния(mergesort). Эти алгоритмы имеют время выполнения O(N * Log(N)). Таким образом, число операций необходимых для сортировки млрд. элементов сокращается до таких разумных пределов, что даже самый дешевый настольный ПК способен провести такую сортировку. Вместо млрд. в квадрате операций (10 18 ) эти алгоритмы требуют только 10 млрд. операций (10 10 ), т.е. в 100 млн. раз быстрее.

Кратчайший путь

Алгоритмы поиска кратчайшего пути из одной точки в другую исследуются уже на протяжении многих лет. Примеров прикладного применения этих алгоритмов предостаточно, однако для простоты изложения будем придерживаться следующей постановки: требуется найти кратчайший путь из точки А в точку Б в городе с несколькими улицами и перекрестками. Существует много разных алгоритмов для решения этой задачи и все они со своими преимуществами и недостатками. Прежде чем мы углубимся в их изучение, давайте рассмотрим время выполнения простого алгоритма перебором. Если алгоритм рассматривает каждый возможный путь от А до Б (который не образует циклов) он вряд ли закончится при нашей жизни, даже если А и Б находятся в маленьком городке. Время выполнения этого алгоритма является экспоненциальным, что обозначается как O(C N ) для некоторого C. Даже для малых значений C, C N становится астрономическим числом, когда N принимает умеренно большое значение.

Один из самых быстрых алгоритмов для решения этой задачи имеет время выполненияO(E+V*Log(V)), где E число дорожных сегментов, а V число пересечений. Алгоритм займет около 2 секунд времени, для поиска кратчайшего пути в городе из 10000 пересечений и 20000 дорожных сегментов (обычно бывает около 2 дорожных сегментов на одно пересечение). Этот алгоритм известен как алгоритм Дейкстры, он является довольно таки сложным и требует использования структуры данных очередь с приоритетом (priority queue). Однако в некоторых случаях даже такое время выполнения является слишком медленным (взять например нахождение кратчайшего пути от Нью-Йорка до Сан-Франциско - в США есть миллионы пересечений), в таких случаях программисты пытаются улучшить время выполнения с помощью так называемой эвристики. Эвристика - это приближенное значение чего-то, что имеет отношение к задаче. В задаче поиска кратчайшего пути, например, может оказаться полезным знать, как далеко находится точка от пункта назначения. Зная это можно разработать более быстрый алгоритм (например алгоритм поиска А* в некоторых случаях работает значительно быстрее чем алгоритм Дейкстры). Такой подход не всегда улучшает время выполнения алгоритма в наихудшем случае, но в большинстве реальных приложений алгоритм начинает работать быстрее.

Приближенные алгоритмы

Иногда даже самый продвинутый алгоритм с самой продвинутой эвристикой работает слишком медленно на самом быстром компьютере. В таких случаях приходится снижать точность конечного результата. Вместо того чтобы пытаться получить кратчайший путь, можно ограничиться путем, который например на 10% больше чем кратчайший путь.

На самом деле есть немало важных задач, для которых известные на сегодня алгоритмы выдают оптимальный результат слишком медленно. Наиболее известная группа из этих задач называется NP (non-deterministic polynomial). Если задача называется NP-полной или NP-трудной, то это означает, что никто не знает достаточно хорошего способа для получения оптимального решения. Кроме того, если кто-то разработает эффективный алгоритм для решения одной NP-трудной задачи, то этот алгоритм можно будет применить ко всем NP-трудным задачам.

Хорошим примером NP-трудной задачи является задача коммивояжёра. Продавец хочет посетить N городов, и он знает, сколько времени занимает перемещение из одного города в другой. Вопрос в том насколько быстро он сможет посетить все города? Самый быстрый из известных алгоритмов для решения этой задачи является слишком медленным - и многие считают, что так будет всегда - поэтому программисты ищут достаточно быстрые алгоритмы, дающие хорошее решение, но часто не оптимальное.

Случайные алгоритмы

Еще один подход, применяемый для решения некоторых задач, заключается в том, чтобы сделать алгоритм случайным. Данный подход не улучшает время алгоритма в худшем случае, но довольно часто хорошо работает в среднем случае. Алгоритм быстрой сортировки является хорошим примером использования рандомизации. В худшем случае, алгоритм быстрой сортировки сортирует группу элементов за O(N 2 ), где N количество элементов. Если в этом алгоритме использовать рандомизацию, то шансы на худший случай становятся незначительно малыми, и в среднем случае алгоритм быстрой сортировки работает за время O(N*Log(N)). Другие алгоритмы даже в худшем случае гарантируют время работы O(N*Log(N)), однако они медленнее в среднем случае. Хотя оба алгоритма имеют время работы пропорциональное N*Log(N), алгоритм быстрой сортировки имеет более меньший постоянный коэффициент (constant factor) - т.е. он требует C*N*Log(N), в то время как другие алгоритмы требуют более 2*C*N*Log(N) операций.

Другой алгоритм, использующий случайные числа ищет медиану для группы чисел и его время работы в среднем случае составляет O(N). Это намного быстрее по сравнению с алгоритмом, который сортирует числа и выбирает среднее, и работает за O(N*Log(N)). Существуют детерминированные алгоритмы (не случайные) которые позволяют найти медиану за время O(N), однако случайный алгоритм проще для понимания и часто работает быстрее этих детерминированных алгоритмов.

Основная идея алгоритма поиска медианы это выбрать среди чисел случайное, и посчитать, сколько чисел в группе меньше чем выбранное число. Допустим, есть N чисел, K из них меньше или равно выбранному числу. Если K меньше чем половина N, тогда мы знаем что медиана это (N/2-K)-е число которое больше чем случайно выбранное число, так что мы отбрасываем K чисел меньших или равных случайному числу. Теперь допустим мы хотим найти (N/2-K)-е наименьшее число, вместо медианы. Алгоритм такой же, мы просто случайно выбираем число и повторяем описанные шаги.

Сжатие

Еще один класс алгоритмов предназначен для сжатия данных. Этот алгоритм не имеет ожидаемого результата (как например, алгоритм сортировки), но вместо этого делается оптимизация по некоторым критериям. В случае сжатия данных, алгоритм (например, LZW) пытается сделать так чтобы данные занимали как можно меньше байтов, но в то же время, чтобы можно было распаковывать их до первоначальной формы. В некоторых случаях этот тип алгоритмов использует те же методы что и другие алгоритмы, что приводит к хорошему результату, но неоптимальному. Например, JPG и MP3 сжимают данные таким образом, что конечный результат получается более низкого качества, чем оригинал, однако и размер меньше. MP3 сжатие не сохраняет каждую особенность оригинального аудио файла, но пытается сохранить достаточно деталей, чтобы обеспечить приемлемое качество и в то же время значительно сократить размер файла. Формат JPG следует тому же принципу, но детали существенно отличаются, т.к. целью является сжатие изображения, а не аудио.

Зачем нужно знать всякие алгоритмы

Чтобы использовать алгоритмы должным образом, важно знать все упомянутые типы алгоритмов. Если вам придется разрабатывать важную часть программного обеспечения, то вы должны быть в состоянии оценить скорость работы вашего алгоритма. Точность вашей оценки зависит от того насколько вы владеете анализом времени исполнения алгоритмов. Кроме этого, необходимо знать детали алгоритмов, что позволит предсказывать особые случаи, в которых программа не будет работать быстро, или будет давать неприемлемые результаты.

Конечно, будут моменты, когда вы будете натыкаться на ранее не изучавшиеся проблемы. В таких случаях нужно придумать новый алгоритм, или по-новому применить старый алгоритм. Чем больше вы знаете об алгоритмах, тем больше у вас шансов найти хорошее решение проблемы. Во многих случаях новая задача легко сводится к старой, но для этого нужно иметь фундаментальное понимание старых задач.

Реальные примеры

Примеров решений реальных задач требующих новейших алгоритмов предостаточно. Почти все, что вы делаете на компьютере зависит от алгоритмов, которые кто-то очень долго разрабатывал. Даже самых простых программ не существовало бы без алгоритмов, которые работают "за сценой" управляя памятью и загружая данные с жесткого диска.

Существуют десятки примеров применения сложных алгоритмов, но обсудим две задачи, решение которых требует таких же навыков, как для решения некоторых задач на TopCoder. Первая задача известна как задача о максимальном потоке, а вторая связана с динамическим программированием - методом который часто позволяет решать задачи с казалось бы невозможной молниеносной скоростью.

Алгоритм поиска максимального потока

Задача поиска максимального потока состоит в том, чтобы посредством имеющейся сети наилучшим образом переместить что-то из одного места в другое. Конкретно такая проблема впервые возникла в 1950-х в связи с железнодорожными путями Советского Союза. США хотели знать, как быстро Советский Союз может подвозить материалы к государствам-сателлитам в Восточной Европе через свою сеть железных дорог.

Кроме того США хотели знать какую часть рельсов можно наиболее легко уничтожить чтобы отрезать государства-сателлиты от остальной части Советского Союза. Оказалось, что эти две задачи тесно связаны и что решение задачи поиска максимального потока также решает задачу о минимальном разрезе, что, в конечном счете, позволит выяснить самый дешевый способ отрезать Советский Союз от своих спутников.

Первый эффективный алгоритм для поиска максимального потока был придуман учеными Фордом и Фалкерсоном. Алгоритм впоследствии был назван алгоритмом Форда - Фалкерсона и является одним из наиболее известных алгоритмов в области компьютерной науки. В последние 50 лет алгоритм претерпел ряд улучшений, что сделало его быстрее (правда, некоторые из этих улучшений устрашают своей сложностью).

Сравнение последовательностей

Многим кодерам за всю свою карьеру ни разу не приходилось реализовывать алгоритм, использующий динамическое программирование. Тем не менее, динамическое программирование применяется в ряде важных алгоритмов. Один из алгоритмов это нахождение различий между двумя последовательностями, который большинство программистов наверняка использовали, хотя возможно и не разбирались в нем. Этот алгоритм вычисляет минимальное количество вставок, удалений, редактирований необходимых для преобразования последовательность A в последовательность B.

Например, рассмотрим последовательности "AABAA" и "AAAB". Для преобразования первой последовательности во вторую самое простое, что нужно сделать это удалить B в середине и изменить последнюю A на B. Этот алгоритм имеет множество применений, включая некоторые задачи связанные с ДНК и обнаружением плагиата. Однако многие программисты используют его в основном для сравнения версий одного и того же файла с исходным кодом. Если элементы последовательности это строки в файле, тот этот алгоритм позволяет узнать какие строки надо удалить, вставить, изменить чтобы преобразовать одну версию файла в другую.

Без динамического программирования приходится перебирать экспоненциальное число преобразований, чтобы перейти от одной последовательности к другой. Однако динамическое программирование сокращает время выполнения алгоритма до O(N*M), где N и M количество элементов в двух последовательностях.

Заключение

Сколько существует различных задач, столько существует и различных алгоритмов для их решения. Тем не менее есть большая вероятность того что задача которую вы пытаетесь решить в некотором смысле похожа на другую задачу. Развивая глубокое понимание широкого диапазона алгоритмов, вы сможете выбрать верный алгоритм и применить его для решения задачи. Кроме того решение задач в соревнованиях на TopCoder поможет вам отточить свои навыки в этой области. Многие из этих задач кажутся искусственными и не реалистичными, но они требуют такого, же набора алгоритмических знаний который требуется каждый день в реальном мире.

Читайте также: