Как сделать усеченную шестигранную пирамиду
. развертку сначала нужно строить развертку целая пирамида потом на ней уже контур вырезан запомните что развертка .
Всем Привет! С вами RAIDO TV и на нашем семейном канале вы увидите кучу крутых ПЛАСТИЛИНовых мастер-классов, .
В этом мастер классе покажу как сделать шестиугольную пирамиду из бумаги. Подпишись на канал, если не подписан .
Всем Привет! С вами RAIDO TV и на нашем семейном канале вы увидите кучу крутых ПЛАСТИЛИНовых мастер-классов, .
Во втором видео-уроке из цикла о пирамиде, как геометрической фигуре в рисунке, мы немного усложним задачу и .
Это наша развертка. Но нам надо сделать из еще натуральный вид сечение для того чтобы мы сделали натуральное .
В этом мастер классе мы сделаем с вами усеченную шестиугольную пирамиду из бумаги своими руками. Подпишись на .
Как построить сечение пирамиды плоскостью. Сечение геометрических тел плоскостью. Начертательная геометрия.
У нас в итоге выходят развертка пирамиды пирамида у нас находится именно такое вертикальное положение без наклона .
Построение аксонометрической проекции усеченной четырехгранной пирамиды во фронтальной диметрии, построение .
Теперь мы можем обрести нашу пирамиду. На нашем чертеже ось прямая а.б. Это пассива не не поэтому она должна быть .
Обучающее видео о том, как построить многогранник, основанием которого является шестиугольник,у которого все углы .
Прямоугольник, квадрат, треугольник, трапеция и другие – геометрические фигуры из раздела точной науки. Пирамида - это многогранник. Основанием этой фигуры является многоугольник, а боковыми гранями треугольники, имеющие общую вершину, или трапеции. Для полного представления и изучения любого геометрического объекта изготавливают макеты. Используют самый разнообразный материал, из которого выполняется пирамида. Поверхность многогранной фигуры, развернутая на плоскости, называется ее разверткой. Создать макет поможет метод преобразования плоских предметов в объемные многогранники и определенные знания из геометрии. Развертки из бумаги или картона изготовить непросто. Потребуется умение выполнять чертежи по заданным размерам.
Материалы и приспособления

Моделирование и выполнение многогранных объемных геометрических фигур - интересный и захватывающий процесс. Из бумаги можно выполнить большое количество всевозможных макетов. Для работы будут необходимы:
- бумага или картон;
- ножницы;
- карандаш;
- линейка;
- циркуль;
- ластик;
- клей.
Определение параметров
Прежде всего определим, какой будет пирамида. Развертка данной фигуры является основой для изготовления объемной фигуры. Выполнение работы потребует предельной точности. При неправильном чертеже геометрическую фигуру собрать будет невозможно. Допустим, необходимо изготовить макет правильной треугольной пирамиды.
Любое геометрическое тело обладает определенными свойствами. Данная фигура имеет основанием правильный многоугольник, а ее вершина спроецирована в его центр. В качестве основания выбран равносторонний треугольник. Данное условие определяет название. Боковые ребра у пирамиды – это треугольники, количество которых зависит от выбранного для основания многогранника. В данном случае их будет три. Также важно знать размеры всех составных частей, из которых будет составлена пирамида. Развертки из бумаги выполняются в соответствии с учетом всех данных геометрической фигуры. Параметры будущей модели оговариваются заранее. От этих данных зависит выбор используемого материала.
Как выполняется развертка правильной пирамиды?
Основой модели является лист бумаги или картона. Работу начинают с чертежа пирамиды. Фигура представляется в развернутом виде. Плоское изображение на бумаге соответствует заранее выбранным размерам и параметрам. Правильная пирамида имеет основанием правильный многоугольник, а высота проходит через его центр. Изготавливаем для начала простую модель. В данном случае – это треугольная пирамида. Определяем размеры выбранной фигуры.
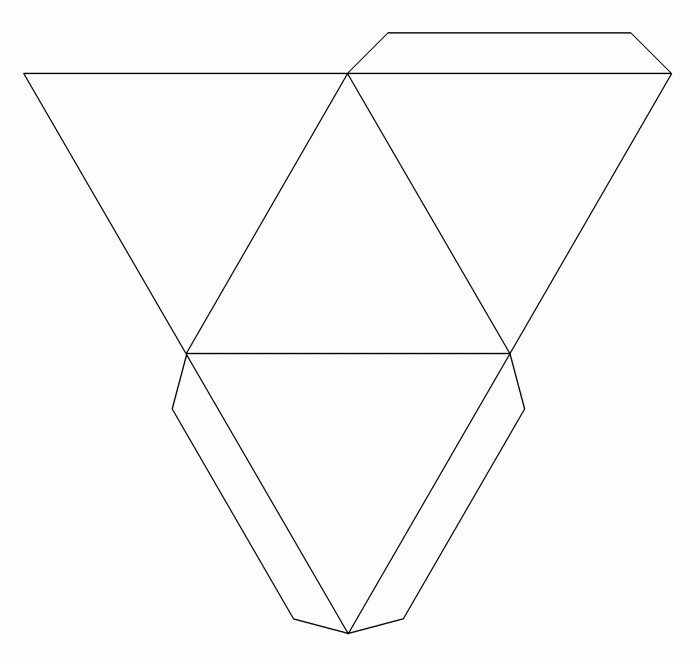
Чтобы построить развертку пирамиды, основанием которой является правильный треугольник, в центре листа, используя линейку и карандаш, нарисуем основание заданных размеров. Далее к каждой его стороне вычерчиваем боковые грани пирамиды – треугольники. Теперь переходим к их построению. Размеры сторон треугольников боковой поверхности измеряем циркулем. Ножку циркуля ставим в вершину нарисованного основания и делаем засечку. Действие повторяем, перемещаясь в следующую точку треугольника. Пересечение, полученное в результате таких действий, определит вершины боковых граней пирамиды. Их соединяем с основанием. Получаем чертеж пирамиды. Для склеивания объемной фигуры на сторонах боковых граней предусматривают клапаны. Дорисовываем небольшие трапеции.
Сборка макета
Вырезаем ножницами выполненный рисунок по контуру. Аккуратно сгибаем развертку по всем линиям. Клапаны-трапеции заправляем внутрь фигуры таким образом, чтобы ее грани сомкнулись. Их смазываем клеем. Через тридцать минут клей высохнет. Объемная фигура готова.
Развертка четырехугольной пирамиды
Сначала представим, как выглядит геометрическая фигура, макет которой будем изготавливать. Основанием выбранной пирамиды является четырехугольник. Боковые ребра - треугольники. Для работы используем те же материалы и приспособления, что и в предыдущем варианте. Чертеж выполняем на бумаге карандашом. В центре листа чертим четырехугольник с выбранными параметрами.
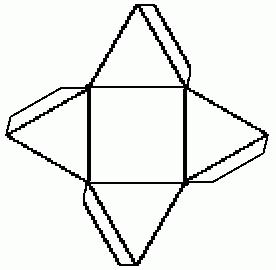
Каждую сторону основания делим пополам. Проводим перпендикуляр, который будет являться высотой треугольной грани. Раствором циркуля, равным длине боковой грани пирамиды, делаем на перпендикулярах засечки, установив его ножку в вершину основания. Оба угла одной стороны основания соединяем с полученной точкой на перпендикуляре. В результате получаем в центре чертежа квадрат, на гранях которого нарисованы треугольники. Чтобы зафиксировать модель на боковых гранях, дорисовывают вспомогательные клапаны. Для надежного крепления достаточно полоски сантиметровой ширины. Пирамида готова к сборке.
Завершающий этап выполнения макета
Полученную выкройку фигуры вырезаем по контуру. По начерченным линиям сгибаем бумагу. Сбор объемной фигуры производят путем склеивания. Предусмотренные клапаны смазываем клеем и фиксируем полученную модель.

Объемные макеты сложных фигур
После выполнения простой модели многогранника можно перейти к более сложным геометрическим фигурам. Развертка пирамиды усеченной намного сложнее в выполнении. Ее основаниями являются подобные многогранники. Боковые грани – это трапеции. Последовательность выполнения работы будет такой же, как та, в которой изготавливалась простая пирамида. Развертка будет более громоздкой. Для выполнения чертежа используют карандаш, циркуль и линейку.
Построение чертежа
Развертка пирамиды усеченной выполняется в несколько этапов. Боковой гранью усеченной пирамиды является трапеция, а основаниями - подобные многогранники. Допустим, что это квадраты. На листе бумаги выполняем чертеж трапеции с заданными размерами. Боковые стороны полученной фигуры продлеваем до пересечения. В результате получаем равнобедренный треугольник. Его сторону измеряем циркулем. На отдельном листе бумаги строим окружность, радиусом которой будет измеренное расстояние.
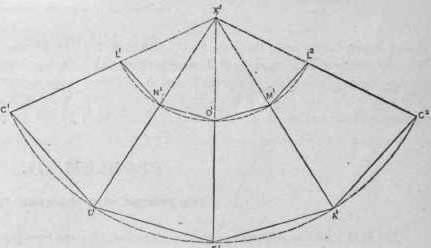
Следующий этап – это построение боковых ребер, которые имеет усеченная пирамида. Развертка выполняется внутри нарисованной окружности. Циркулем измеряют нижнее основание трапеции. На окружности отмечаем пять точек, которые соединяют линии с ее центром. Получаем четыре равнобедренных треугольника. Циркулем измеряем сторону трапеции, нарисованной на отдельном листе. Данное расстояние откладываем на каждой стороне нарисованных треугольников. Полученные точки соединяем. Боковые грани трапеции готовы. Остается только нарисовать верхнее и нижнее основания пирамиды. В данном случае это подобные многогранники – квадраты. К верхнему и нижнему основаниям первой трапеции дорисовываем квадраты. На чертеже изображены все части, которые имеет пирамида. Развертка практически готова. Остается только дорисовать соединительные клапаны на сторонах меньшего квадрата и одной из граней трапеций.
Завершение моделирования
Перед склеиванием объемной фигуры чертеж по контуру вырезают ножницами. Далее развертку аккуратно сгибают по начерченным линиям. Крепежные клапаны заправляем внутрь модели. Их смазываем клеем и прижимаем к граням пирамиды. Модели даем высохнуть.

Изготовление разных моделей многогранников
Выполнение объемных моделей геометрических фигур - увлекательное занятие. Чтобы его досконально освоить, следует начинать с выполнения самых простых разверток. Постепенно переходя от простых поделок к более сложным моделям, можно приступать к созданию самых замысловатых конструкций.
Сечение пирамиды SABCDE плоскостью α(αH, αV) выполнено ранее. Развертка боковой поверхности пирамиды будет представлять собой плоскую фигуру, состоящую из треугольников, являющихся гранями пирамиды. Развертка поверхности усеченной пирамиды строится в два этапа.

Этап первый - построение действительной величины сечения. Выполняется способом вращения вокруг следа плоскости αH: - взяв на следе плоскости αV произвольную точку 6(6", 6`), строим ее совмещенное положение с плоскостью H - 60; - строим совмещенное положение с плоскостью H фронтального следа плоскости αV - αV0 по точкам αx и 60; - строим совмещенное положение с плоскостью H точки сечения 1 - 10 находим на пересечении соответствующей фронтали плоскости α с проекцией линии вращения; - аналогично строим совмещенное положение с плоскостью H остальных точек сечения 2, 3, 4, 5 - 20, 30, 40, 50. Данные построения выделены зеленым цветом.
Развертка поверхности усеченной пирамиды - этап второй. Построение выделено синим цветом. Построение развертки выполняем способом треугольников: - Определяем действительную величину ребер пирамиды способом вращения их вокруг оси i ∋ S также i ⊥ H, в том же ключе строим действительную величину ребер усеченной пирамиды: A1, B2, C3, D4, E5; - на прямой a произвольного положения откладываем величину |S0A0| ≅ |S"A2|; - из точки A0 проводим дугу радиусом r1 = |A`B`|; - из точки S0 проводим дугу радиусом RB = |S"B2|; - пересечение дуг r1 и RB определяет положение вершины B0 треугольника ΔS0B0A0. ΔS0B0A0 ≅ ΔSBA - грани пирамиды; - из точки S0 проводим дугу радиусом R1 = |S"1"0|, из точки S0 проводим дугу радиусом R2 = |S"2"0|; - пересечение дуги R1 и S0A0 а также R2 и S0B0 определяет положение вершин 10 и 20. 1020B0A0 ≅ 12BA - грани усеченной пирамиды;
Развертка поверхности усеченной пирамиды продолжается таким же образом и для остальных ее граней. К построенной развертке боковой поверхности усеченной пирамиды присоединяем основание A0B0C0 D0E0 и сечение 1020304050, которые строим способом триангуляции.
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты . Возможно очное и дистанционное обучение по Skype: 1000 р./ак.ч.
6.1. Пирамида. Сечение пирамиды плоскостью. Развертка пирамиды
Многогранником называется тело, ограниченное плоскими многоугольниками, которые называется гранями.
Грани, пересекаясь, образуют ребра .
Ребра, пересекаясь, образуют вершины .
Рассмотрим два основных вида многогранников:
Пирамида – многогранник, у которого боковыми гранями являются треугольники, а основанием – многоугольник.
Упражнение
Дана пирамида, основание которой параллельно π1. Основание представляет собой некоторый треугольник.

S – вершина пирамиды (Рисунок 6.1).
Рисунок 6.1 – Пересечение поверхности пирамиды прямой
Требуется построить точки пересечения прямой m общего положения с поверхностью пирамиды.
- Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π2.
- Строим сечение ∆ (123) поверхности пирамиды с плоскостью σ.
Решение задачи сводится к нахождению линии пересечения плоскостей общего положения (боковые грани пирамиды) и плоскости частного положения (плоскость σ).
Примечание. При наличии круто падающих рёбер (близких к вертикали), построение недостающей проекции точки на ребре по одной данной проекции необходимо выполнять при помощи пропорционального деления отрезка.
- В сечении находим точки M и N принадлежащие прямой m.
- Определяем видимость прямой m.
Развёрткой многогранника называется фигура, полученная в результате последовательного совмещения граней многогранника с плоскостью.
Развёртка всегда строится наружной (лицевой) стороной к наблюдателю.
Для построения развёртки пирамиды нужно определить истинные величины всех рёбер пирамиды и построить грани пирамиды в виде треугольников, последовательно присоединяя их друг к другу.
Основание можно присоединить к любой грани, например, АС (Рисунок 6.2).

Рисунок 6.2 – Построение развёртки пирамиды
В упражнении истинные значения ребер определены способом вращения. Для построения линии сечения на развертке, на истинных величинах рёбер построим точки \overline,\overline,\overline , проведя горизонтальные линии (траектории перемещения точек 1, 2, 3) до пересечения с соответствующими истинными проекциями ребер.
6.2. Призма. Развертка призмы
Призма – многогранник, у которого боковыми гранями являются параллелограммы, а основания – многоугольники, лежащие в параллельных плоскостях.
Упражнение
Дана призма, основания которой параллельны плоскости проекций π1.
Требуется построить точки пересечения прямой m с поверхностью призмы (Рисунок 6.3).
- Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π2.
- Строим сечение поверхности призмы с плоскостью σ →(∆(123)).
- В сечении находим точки K и L принадлежащие прямой m.
- Определяем видимость прямой m. Если грань АВ на π2 видна, то точка К на π2 видима, грань ВС невидима, следовательно, точка Lневидима.
Рассмотрим наклонную призму. Пусть основание призмы параллельно π1, а ребра параллельны π2.
Построим нормальное сечение, то есть сечение плоскостью σ, перпендикулярной ребрам призмы (Рисунок 6.4).
Это сечение развернется в прямую линию. Боковые ребра перпендикулярны к линии сечения.

Рисунок 6.4 – Построение развёртки призмы
Порядок построения :
- Найдем истинную величину сечения – (102030), для чего повернём сечение (123) вокруг оси n⊥π2, (можно ввести ДПП π3//σ).
- Проведём горизонтальную линию на свободном месте листа. Отложим на ней отрезки:
/10-20/; /20-30/; /30-10/.
- Проведём направления рёбер перпендикулярно этой линии через точки: 10; 20; 30 и отмерим вверх и вниз расстояния от нормального сечения (на π2) до верхнего и нижнего основания, откладывая их на линиях-ребрах.
6.3. Взаимное пересечение многогранников
В результате пересечения многогранников получим ломаную линию.
Возможны два случая пересечения многогранников (Рисунок 6.5):

Рисунок 6.5 – Варианты пересечения многогранников
Вершины ломаной – точки пересечения рёбер одного многогранника с гранями другого.
Звенья ломаной – линии пересечения граней.
Для решения задачи нужно найти вершины ломаной, то есть точки пересечения всех рёбер, участвующих в пересечении.
Построенные точки соединить.
Упражнение

Построить линии пересечения призмы с пирамидой (Рисунок 6.6).
Рисунок 6.6. Построение линии пересечения призмы с пирамидой
Решение
- Находим на π2 проекции точек пересечения ребра пирамиды с проецирующими гранями призмы (точки 12 и 22). Находим их горизонтальные проекции.
- Строим точки пересечения ребра призмы с боковыми гранями пирамиды (точки 32 и 42), для чего используем вспомогательную плоскость τ⊥π2.
- Полученные на π1 точки 3, 2, 4, 1 соединяем отрезками прямых. Причем отрезки 11-31, 11-21, 11-41 невидимы. Получили замкнутую линию пересечения пирамиды с призмой.
Упражнение
остроить три проекции пирамиды с вырезом и развертку (Рисунок 6.7).
- По двум проекциям построить третью;
- На всех трех проекциях построить проекции линии пересечения призматического выреза с пирамидой;
- Невидимые участки линии пересечения и участки рёбер многогранников показывать штриховой линией;
- Построить развёртку пирамиды с нанесением линии пересечения.

Рисунок 6.7. Построение проекций пирамиды с вырезом и развертки
Решение :
- Проводим линии рёбер призмы на всех проекциях.
- Введём плоскость σ⊥π2, σ//π1:
- σ//АВС – основанию пирамиды;
- σ пересекает пирамиду сечение подобно ΔА1В1С1.
Это сечение пересекается:
— с ребром D в двух точках 1 и 4;
— с ребром Е в двух точках 2 и 5.
Соединим найденные точки: 1-2-3-1; 4-6-5-7-4 и определим видимость.
Построение развертки рассмотрено ранее.
6.4. Задачи для самостоятельной работы
1-4. Построить линию пересечения гранных поверхностей. Показать видимость (Рисунки 6.8 – 6.11).
Рисунок 6.8
Рисунок 6.9
Рисунок 6.10
Рисунок 6.11
По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты . Возможно очное и дистанционное обучение по Skype: 1000 р./ак.ч.
Здравствуйте, друзья! В этой статье предложено рассмотреть два случая построения сечения шестиугольной пирамиды. Пирамида всегда “рассекается” сложнее, чем призма, а чем больше у нее углов в основании, тем труднее. В первой задаче я постаралась пользоваться методом следов, а во второй – преимущественно использован метод внутреннего проецирования. Так как чертежи насыщены построениями, я использовала разные цвета, и не всегда соблюдала правило “невидимое – пунктиром”. Постараюсь сопроводить картинки подробным описанием.
Задача 1. Построить сечение правильной шестиугольной пирамиды плоскостью, проходящей через заданные точки.

Шаг 1. Точки и лежат в плоскости основания пирамиды, что для нас очень удобно. Проведем прямую , она пересечется с лучом плоскости основания. За счет принадлежности обеим прямым – и точка принадлежит как плоскости грани , так и секущей плоскости.

Шаг 2. Через точки и можем проводить прямую, она пересечет ребро в точке .

Шаг 3. Так как прямая , также принадлежащая плоскости основания, не параллельна , то она пересечет эту прямую, и таким образом, можно было бы получить точку плоскости грани . Но пересечение этих прямых – за границами чертежа. Где невозможно применение метода следов, на помощь приходит метод внутреннего проецирования. Проведем прямую и ее проекцию в плоскости основания – .

Шаг 4. Проведем проекцию будущей прямой секущей плоскости – (просто соединим вершины). пересечет в точке , – в точке . Из точки поднимемся вверх до секущей плоскости – построим перпендикуляр к плоскости основания . – точка прокола перпендикуляром секущей плоскости.

Шаг 5. Точка принадлежит секущей плоскости, точка – также. Проводим прямую . Прямая пересечет ребро в точке (поздно было переделывать картинку, пусть уж будет вторая точка ). Она принадлежит обеим плоскостям – и , и .

Шаг 6. Вернемся к методу следов. Проводим прямую , и ищем ее пересечение с . Это точка . Она лежит в плоскости грани .

Шаг 7. Проводим , эта прямая пересечет ребро в точке .

Шаг 8. Соединим полученные точки отрезками.

Окончательный вид сечения с противоположной стороны.

Окончательный вид сечения.
Задача 2. Построить сечение правильной шестиугольной пирамиды плоскостью, проходящей через заданные точки.

Задача 2. Шаг 1. Проводим диагонали основания пирамиды , , . Из точек и секущей плоскости опускаем перпендикуляры к основанию, определяем точки и , в которых эти перпендикуляры достигнут основания пирамиды.

Шаг 2. Проводим прямые и секущей плоскости и их проекции и . Проекцией прямой будет прямая . Определяем точку пересечения и , и из этой точки поднимаем перпендикуляр до пересечения с – получили точку .

Шаг 3. Из точки , которая является пересечением диагонали и проекции , поднимаем перпендикуляр до пересечения с – получаем точку . Из точки , которая является пересечением диагонали и проекции , поднимаем перпендикуляр до пересечения с – получаем точку . Через точки и проведем прямую, которая пересечет ребро пирамиды в точке .

Шаг 4. Через точки и также проведем прямую. Определим место пересечения ею ребра – точку . Осталось найти две точки – на ребре и на ребре .

Шаг 5. Проведем прямую – продолжение ребра основания. Также через точки и проведем прямую, принадлежащую грани . Найдем место пересечения прямых и – точку .

Шаг 6. Через точки и секущей плоскости, лежащие в основании, проводим прямую, которая пересечет ребро в точке .

Шаг 7. Прямая пересечет продолжение диагональ в точке . Проведем прямую через точки и , чтобы определить точку пересечения этой прямой с ребром – точку .
Читайте также:


