Как сделать тетраэдр
Развертка и схема тетраэдра. Как сделать тетраэдр из бумаги самому
Из истории
Тетраэдр еще одна удивительная фигура, которая довольно часто встречается в нашей жизни, но обычно наши знания о нем ограничиваются определением, свойствами и формулами из школьного курса геометрии.
Слово "тетраэдр" образовано из двух греческих слов: tetra – переводиться как четыре и hedra – означает основание, грань; в каждой вершине тетраэдра сходятся по 3 грани. Эта фигура имеет 4 грани, 6 ребер и 4 вершины.
С самых древних времен представления людей о красоте были связаны с симметрией. Возможно, этим объясняется интерес людей к многогранникам – удивительным символам симметрии, привлекавшим внимание выдающихся мыслителей и людей всех эпох. Уже во времена Пифагора дивились их красоте и симметрии. Ученики Пифагора считали, что правильные многогранники – это божественные фигуры и использовали их в философских сочинениях. Первоосновам бытия – огню, воздуху, воде, земле придавалась форма соответственно октаэдра, икосаэдра, тетраэдра, куба, а Вселенная представлялась в форме додекаэдра. Ученики Платона продолжили изучение перечисленных тел, поэтому эти многогранники называют Платоновыми телами.
Роль задач о тетраэдрах очень высока в развитии математического мышления школьников. Эти задачи стимулируют накопление геометрических представлений и знаний, способствуют развитию пространственного мышления, что особенно важно в процессе изучения стереометрии.
Где можно встретить тетраэдр? Тетраэдр, такая удивительная геометрическая фигура, которая встречается нам повсюду, но с первого взгляда ее не так просто заметить. Тетраэдр может образовать жёсткую конструкцию. Выполненный из стержней, его часто используют в качестве основы для пространственных конструкций балок, ферм мостов, пролётов зданий, перекрытий и т. д. Прямоугольный тетраэдр давно используется в оптике. На велосипедах отражатели катафоты имеют форму тетраэдра. Благодаря свойствам тетраэдра, катафоты отражают свет и другим людям и водителям видно велосипедиста. Если внимательно присмотреться, то внутри катафота видно множество форм тетраэдра.
Виды тетраэдра
Фигуру тетраэдр можно разделить на несколько видов, какие они бывают?
Равногранный тетраэдр, все его грани являются равными между собой треугольниками;
Ортоцентрический тетраэдр, высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке;
Прямоугольный тетраэдр, ребра, прилежащие к одной из вершин, являются перпендикулярными между собой;
Правильный тетраэдр, это тетраэдр, грани которого являются равносторонними треугольниками,
Инцентрический тетраэдр, его отрезки соединяют вершины с центрами окружностей, которые вписаны в противоположные грани и пересекаются в одной точке.
Выделяют так же каркасный тетраэдр, соразмерный тетраэдр.
Тетраэдр – подсказанное нам природой идеальное равновесие, в основе которого, идеальность равнобедренного треугольника. Тетраэдр – треугольник, но только в объемном виде, в наше время его можно назвать 3D треугольник.
Пополнить свою коллекцию геометрических фигур новой фигурой – тетраэдром, вы можете используя развертки, представленные на нашем сайте. Тетраэдр, собранный по этим разверткам можно использовать для обучения, например, что бы научить детишек считать, узнавать цвета, можно объяснить, что такое плоскость и объем, что такое треугольник др.
Тетраэдр – самая простая фигура из многоугольников. Он состоит из четырех граней, каждая из которых представляет собой равносторонний треугольник, при этом каждая из сторон соединяется с другой всего лишь одной гранью. При изучении свойств этой трехмерной геометрической фигуры для наглядности лучше всего сделать модель тетраэдра из бумаги.
Как склеить тетраэдр из бумаги?
Для построения простого тетраэдра из бумаги нам понадобится:
- собственно бумага (плотная, можно использовать картон);
- транспортир;
- линейка;
- ножницы;
- клей;
- тетраэдр из бумаги, схема.
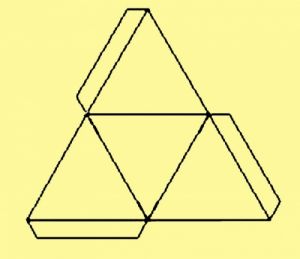
- Работу над тетраэдром начинаем с рисования развертки из бумаги. Если выполнение фигуры планируется из обычной бумаги, можно чертить развертку прямо на ней.
- Чертим прямую, которая будет являться гранью тетраэдра. С двух концов откладываем углы по 60 ⁰ , а через полученные точки проводим прямые линии до их пересечения. У нас получился равносторонний треугольник.
- Далее на каждой стороне полученного треугольника строим такие же. От каждого конца снова откладываем по 60 ⁰ и соединяем. В результате должна получиться схема, состоящая из четырех равносторонних треугольников.
- Для того, чтобы развертку можно было склеить и получить тетраэдр, следует сделать припуски по 1 см с трех сторон разных треугольников. В результате получается вот такой чертеж .
- Вырезаем развертку и сгибаем ее по всем линиям, припуски загибаем внутрь, если нужно, обрезаем углы. Мажем их клеем и прижимаем ко внутренним сторонам граней, состыковав линию сгиба между стороной и припуском со стороной свободного треугольника.
Несколько дополнительных рекомендаций:
- если бумага очень плотная, то по местам сгибов следует провести твердым предметом, например, ребром линейки;
- для того, чтобы получить разноцветный тетраэдр, можно раскрасить грани или выполнить развертку на листах цветной бумаги.
Как из бумаги сделать тетраэдр без склеивания?
Предлагаем вашему вниманию мастер-класс, в котором рассказывается, как собрать 6 тетраэдров из бумаги в единый модуль при помощи техники оригами.
- 5 пар квадратных листов бумаги различных цветов;
- ножницы.
Если вы справились с тетраэдром, можно продолжить и смастерить из бумаги призму, икосаэдр, параллелепипед и другие геометрические фигуры.
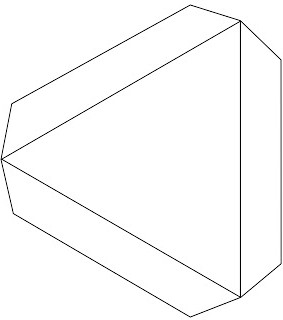
Если вдруг вам дали задание на уроке геометрии или само по себе возникло желание освежить в памяти свойства объемных фигур, то вам непременно следует прочесть о том, как из бумаги сделать тетраэдр, и обязательно применить наши советы на практике. Ведь эта фигура благодаря своей простоте является одной из базовых моделей трехмерного моделирования.
Само слово "тетраэдр" можно перевести с греческого как "четырехгранник". И правда, рассматриваемый объект имеет четыре треугольные грани, а также четыре вершины и шесть ребер. Существует несколько подвидов данной фигуры, но мы не будем обсуждать все возможные варианты. В этой статье вы сможете узнать о способах, как из бумаги сделать
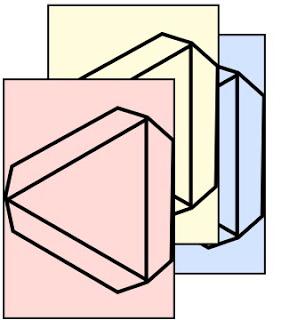
Для работы не понадобится вдаваться в сложные математические вычисления, не придется рассчитывать ни обьем тетраэдра, ни его площадь, ни высоту. Единственное, что потребуется, - это лист бумаги, карандаш, ножницы и клей, а то и восве можно обойтись только бумагой.
Так как из бумаги сделать тетраэдр, имея все необходимые материалы? Существует несколько способов. Первый и самый распространенный вариант: вырезать четыре отдельных треугольника с так называемыми "лепестками", которые затем склеиваются между собой. Вы можете нарисовать равносторонний треугольник самостоятельно или же воспользоваться готовым шаблоном. К преимуществам этого способа можно отнести

возможность сделать фигуру разноцветной, взяв бумагу разных цветов и оттенков. Это придаст изделию яркость и более интересный вид.
Второй способ заключатся в склеивании не отдельных треугольников, а уже соединенных между собой (так называемая развертка тетраэдра). В этом случае тоже может быть несколько вариантов, а именно: лепестки для склейки могут находиться на всех открытых гранях или же только на некоторых, тех, которые представляют минимум для надежной фиксации.
И, наконец, рассматривая третий способ того, как из бумаги сделать тетраэдр, мы увидим, что нет нужды даже в каких-либо клеящих веществах, ведь

еще одним вариантом сборки данной геометрической фигуры является модульное оригами. Вот такую полую пирамиду можно сделать, применив данный метод, имея в запасе достаточное количество бумаги, усидчивости и терпения. В целом, это не очень сложная, но довольно кропотливая работа, и в этой статье мы не будем приводить подробных инструкций. Если вас заинтересует данная информация, вы сможете найти ее в источниках, посвященных этому японскому искусству. И, если вы все-таки дадите себе труд разыскать инструкцию к этой поделке, в скором времени у вас легко получится даже такая сложная конструкция.

Каждый из перечисленных выше вариантов имеет свои преимущества перед остальными, и все они являются достойными и эффективными. И выбирать способ, который подходит именно вам, следует, опираясь на наличие времени и терпения, а также предназначение будущей модели тетраэдра.
Тетраэдр (четырёхгранник) - многогранник с четырьмя треугольными гранями, в каждой из вершин которого сходятся по 3 грани.

У тетраэдра 4 грани, 4 вершины и 6 рёбер.
В данном случае я привожу развёртку правильного тетраэдра, у которого все грани - равносторонние треугольники. На сайте Википедии можно подробно прочитать о различных видах тетраэдров, расчётов объёма, применении этой фигуры и пр.
Читайте также:


