Как сделать таблицу относительных частот в процентах
Я новичок в R. Мне нужно создать простую таблицу частот (как в книгах) с кумулятивной частотой и относительной частотой.
поэтому я хочу генерировать из некоторых простых данных, таких как
Я знаю, что это должно быть просто, но я не знаю, как.
я получил некоторые результаты, используя этот код:
ты близко! Есть несколько функций, которые сделают это легким для вас, а именно cumsum() и prop.table() . Вот как бы я, наверное, все это сложил. Я делаю некоторые случайные данные, но суть одна и та же:
базовые функции table , cumsum и prop.table должен доставить вас туда:
С cbind и именования столбцов по своему вкусу это должно быть довольно легко для вас в будущем. Выход из функции таблицы является матрицей, поэтому этот результат также является матрицей. Если бы это делалось на чем-то большом, было бы эффективнее сделать следующее:
если вы ищете что-то предварительно упакованные, рассмотрим!--4-- функция> от descr пакета.
или, чтобы получить кумулятивные проценты, используйте ordered() функции
чтобы добавить столбец "кумулятивные частоты":
если в данных отсутствуют значения, в таблицу добавляется допустимый столбец процентов.
Очень часто из-за дороговизны или слишком большого числа наблюдений невозможно получить полной информации об объектах, событиях или наблюдениях. По этой причине информацию получают на основе анализа части всего множества объектов, событий или наблюдений, называемой рядом числовых данных, рядом выборочных данных или, просто, выборкой.
Выборка представляет собой конечный ряд чисел (выборочных данных), количество чисел в котором называют объемом выборки
Для обеспечения достоверности информации об объектах, событиях или наблюдениях, полученных на основе статистических исследований числовых рядов (анализа выборочных данных), отбор выборочных данных должен носить случайный характер и иметь достаточно большой объем, то есть выборка должны быть репрезентативной (представительной).
Статистические исследования числовых рядов (рядов чисел, рядов выборочных данных) удобно проводить в соответствии со следующей схемой, которую мы изложим на примере следующей выборки X :
Определяем объем выборки (число чисел в числовом ряде).
В числовом ряде (1) десять чисел, поэтому объем выборки равен 10.
Вычисляем среднее арифметическое числового ряда X (среднее выборочное значение), которое обозначают .
Для числового ряда (1)
Производим упорядочение числового ряда по возрастанию (ранжирование числовых данных). Полученный числовой ряд, который обозначим X1 , называют вариационным рядом.
Для числового ряда X вариационный ряд X1 имеет следующий вид:
Вычисляем размах числового ряда X , то есть разность между наибольшим числом из числового ряда и наименьшим числом из числового ряда.
В числовом ряде X , как и в вариационном ряде X1 , число 3,44 является наибольшим числом, а число 3,12 является наименьшим числом. Поэтому размах числового ряда X равен
Вычисляем медиану числового ряда.
В случае, когда объем выборки (число членов числового ряда) – чётное число, медианой числового ряда является число, равное половине суммы двух чисел, стоящих в середине вариационного ряда.
Число членов ряда X равно чётному числу 10 , а в середине вариационного ряда X1 стоят числа 3,24 и 3,25 . Поэтому медиана числового ряда, которую обычно обозначают символом Me , равна
В случае, когда объем выборки (число членов числового ряда) – нечётное число, медианой числового ряда является число, стоящее в середине вариационного ряда.
Например, медианой числового ряда
является число 7 .
Составляем таблицу частот числового ряда.
Если взглянуть на числа (выборочные данные), составляющие вариационный ряд X1 , то можно заметить, некоторые числа повторяются, а другие встречаются лишь по одному разу. Это наблюдение приводит к следующему определению.
ОПРЕДЕЛЕНИЕ 1 . Если выборочное данное встречается в вариационном ряде m раз, то число m называют частотой (абсолютной частотой) этого выборочного данного.
Воспользовавшись определением 1, сформируем для числового ряда X таблицу, содержащую две строки, которую называют таблицей частот (абсолютных частот) числового ряда. Для этого в первой строке таблицы запишем числа, составляющие вариационный ряд X1 , причем запишем числа в порядке возрастания и без повторений. Во второй строке таблицы запишем частоты (абсолютные частоты), соответствующие числам из первой строки таблицы.
ТАБЛИЦА ЧАСТОТ ЧИСЛОВОГО РЯДА
| Числа, составляющие вариационный ряд (без повторений) | 3,12 | 3,24 | 3,25 | 3,34 | 3,37 | 3,44 |
| Частоты | 3 | 2 | 1 | 1 | 1 | 2 |
| Числа, составляющие вариационный ряд (без повторений) | Частоты |
| 3,12 | 3 |
| 3,24 | 2 |
| 3,25 | 1 |
| 3,34 | 1 |
| 3,37 | 1 |
| 3,44 | 2 |
ЗАМЕЧАНИЕ. Сумма частот, то есть сумма чисел, записанных во второй строке таблицы частот числового ряда, равна объему выборки (числу чисел в числовом ряде). В рассматриваемом случае это число 10 .
Составляем таблицу относительных частот (в процентах).
ОПРЕДЕЛЕНИЕ 2 . Относительной частотой (в процентах) выборочного данного называют число процентов, которое составляет частота этого выборочного данного от всего объема выборки (количества членов числового ряда).
Для того, чтобы сформировать таблицу относительных частот числового ряда, заменим частоты, записанные во второй строке таблицы частот числового ряда, на соответствующие им относительные частоты. В результате получим следующую таблицу.
ТАБЛИЦА ОТНОСИТЕЛЬНЫХ ЧАСТОТ (В ПРОЦЕНТАХ)
| Числа, составляющие вариационный ряд (без повторений) | 3,12 | 3,24 | 3,25 | 3,34 | 3,37 | 3,44 |
| Относительные частоты (%) | 30% | 20% | 10% | 10% | 10% | 20% |
| Числа, составляющие вариационный ряд (без повторений) | Относительные частоты (%) |
| 3,12 | 30% |
| 3,24 | 20% |
| 3,25 | 10% |
| 3,34 | 10% |
| 3,37 | 10% |
| 3,44 | 20% |
Находим моду числового ряда.
ОПРЕДЕЛЕНИЕ 3 . Модой числового ряда называют выборочное данное с наибольшей частотой.
Из таблицы частот числового ряда видно, что модой числового ряда X является число 3,12 , поскольку его частота 3 является наибольшей. Очевидно, что и относительная частота этого выборочного данного является самой большой (30%) .
ЗАМЕЧАНИЕ . Объем выборки, среднее выборочное значение, размах, медиана и мода числового ряда являются одними из статистических характеристик числовых рядов.
При анализе данных периодически возникает задача подсчитать количество значений, попадающих в заданные интервалы "от и до" (в статистике их называют "карманы"). Например, подсчитать количество звонков определенной длительности при разборе статистики по мобильной связи, чтобы понимать какой тариф для нас выгоднее:

Для решения подобной задачи можно воспользоваться функцией ЧАСТОТА (FREQUENCY) . Ее синтаксис прост:
=ЧАСТОТА( Данные ; Карманы )
- Карманы - диапазон с границами интервалов, попадание в которые нас интересует
- Данные - диапазон с исходными числовыми значениями, которые мы анализируем
Для использования функции ЧАСТОТА нужно:
- заранее подготовить ячейки с интересующими нас интервалами-карманами (желтые F2:F5 в нашем примере)
- выделить пустой диапазон ячеек (G2:G6) по размеру на одну ячейку больший, чем диапазон карманов (F2:F5)
- ввести функцию ЧАСТОТА и нажать в конце сочетание Ctrl+Shift+Enter, т.е. ввести ее как формулу массива
Кроме того, с помощью функции ЧАСТОТА можно легко подсчитывать количество уникальных чисел в наборе с помощью простой формулы массива:
Выбор количества групп
Количество групп, выбранных для группировки данных, непосредственно зависит от объема исходной выборки. Чем больше элементов содержит выборка, тем больше групп можно создать. Как правило, распределение частот должно содержать не менее 5 и не более 15 групп. Если групп слишком мало или слишком много, новую информацию получить сложно. Выделение групп процесс творческий, и я бы рекомендовал в качестве первого подхода использовать формулу Стерджесcа:
где k – число групп, n – объем выборки; далее визуально определить по графику, насколько удачным получилось разбиение и, если требуется, скорректировать число групп на величину ± 1.
Вычисление интервала группирования
Каждая группа, образующая распределение частот, должна иметь одинаковый размах. Чтобы определить ширину интервала группирования, диапазон изменения данных делят на заданное количество групп.
(2) Ширина интервала группирования = Диапазон / Количество групп
В нашем примере (см. первое упоминание в заметке Как упорядочить массив данных) имеются данные о 158 фондах (рис. 1).

Рис. 1. Упорядоченный массив, содержащий данные о пятилетней среднегодовой доходности 158 фондов, ориентированных на быстрый рост капитала, за период с 1 января 1997 до 31 декабря 2001
Для такого массива достаточно создать восемь групп (k = 1 + log2158 = 8,3). Диапазон значений массива вычисляется по формуле 26,3 – (–6,1) = 32,4. С учетом формулы (2) ширина интервала группирования = 32,4 / 8 = 4,05. Для удобства округляем до 5 (в меньшую сторону округлять нельзя, так как какие-то значения выпадут из рассмотрения).
Вычисление границ групп
Для вычисления распределения частот необходимо так определить границы групп, чтобы они не пересекались. Перекрытие групп не допускается. Поскольку размах каждой группы, построенной на основе данных о пятилетней среднегодовой доходности фондов, равен 5%, границы групп должны быть установлены так, чтобы учесть все данные. По возможности эти границы должны быть достаточно наглядными. Например, величины из первой группы должны изменяться в диапазоне от –10% до –5% и так далее, пока не будут сформированы 8 неперекрывающихся групп, ширина каждой из которых равна 5% (рис. 2).

Рис. 2. Распределение частот для пятилетней среднегодовой доходности 158 фондов
Главным преимуществом этой таблицы является возможность легко вычислять основные характеристики данных. Например, таблица демонстрирует, что диапазон среднегодовой доходности 158 фондов ограничен числами –10% и 30%, причем показатели в основном группируются в диапазоне 5…15%.
С другой стороны, эта сводная таблица имеет недостаток: по ней невозможно определить, как распределены индивидуальные данные внутри групп. Например, доходность трех фондов из представленных в таблице, изменяется в диапазоне 20–25%, но определить, вокруг какого значения они сконцентрированы (20 или 25%), невозможно. Для представления средней доходности этих трех фондов выбирается срединная точка (22,5%). Срединной точкой интервала –10…–5%, является значение –7,5% и т.д.
Субъективность при выборе границ групп
Выбор границ групп при вычислении распределения частот является субъективным. Если наборы данных невелики, одинаковый выбор границ групп для разных выборок может привести к разным результатам. Например, если при вычислении распределения частот для показателей пятилетней среднегодовой доходности ширину интервалов группирования установить равной 4%, а не 5%, возникнет смещение распределения. Особенно сильно этот эффект проявляется при работе с малыми выборками.
Смещение распределения возникает не только в результате изменения границ групп. Например, ширину интервала группирования можно оставить равной 5%, изменив границы первой и последней групп. Эта манипуляция также приводит к смещению распределения, особенно, если объем выборки невелик. К счастью, по мере увеличения объема выборки этот эффект становится менее выраженным.
Распределение относительных частот и процентное распределение
Для более углубленного анализа распределения частот можно построить либо распределение относительных частот (долей) либо процентное распределение. Выбор распределения зависит от того, с какими данными желает работать пользователь: с долями или процентами (рис. 3).
Рис. 3. Распределение относительных частот и процентное распределение для пятилетней среднегодовой доходности 158 фондов
Таким образом, доля фондов, ориентированных на быстрый рост капитала, среднегодовая доходность которых изменяется от 10 до 15%, равна 0,386, а процент — 38,6%. Работать с долями или процентами удобнее, чем с количеством элементов в группе. Распределение относительных частот, как и процентное распределение, позволяет сравнивать даже наборы данных, имеющие разные объемы.
Функция распределения
Часто оказывается полезной таблица интегральных процентов, которую также называют распределением интегральных процентов. Функция распределения позволяет обнаружить информацию, которая ускользает от распределения частот (рис. 4). (Для построения распределение интегральных процентов были использованы данные, приведенные на рис. 3.)

Рис. 4. Распределение интегральных процентов
Для вычисления распределения частот можно воспользоваться командой Данные → Анализ данных (рис. 5).

Рис. 5. Анализ данных
Если надстройка Анализ данных не отражается, ее нужно предварительно установить. Выберите меню Файл → Параметры (рис. 6). В открывшемся окне Параметры Excel, выберите меню Надстройки → Пакет анализа и кликните на кнопке Перейти.

Рис. 6. Параметры Excel
В открывшемся окне Надстройки поставьте галочку на опции Пакет анализа и кликните Ok (рис. 7).

Рис. 7. Надстройки
Теперь нужно подготовить исходные данные. Расположим числа доходности 158 фондов (как на рис. 1) в столбце А (рис. 8). Вообще говоря, это не обязательно. Можно расположить данные и в виде двумерного массива, как на рис. 1. В столбце С размещаем упорядоченный массив верхних границ диапазонов. Именно этот массив и будет чуть позже введен в поле Интервал карманов. Здесь есть маленькая тонкость. Excel включит верхнюю границу в диапазон. Например, интервал, для которого указана верхняя граница 10, фактически является интервалом 5,00001…10. Именно к этому интервалу будет относиться число 10, а не к следующему интервалу 10…15. Можно сказать и иначе: нижняя граница не входит в интервал, а верхняя – входит. Запускаем надстройку Анализ данных, из списка Инструменты анализа выбираем пункт Гистограмма, жмем ОК.
Рис. 8. Подготовка исходных данных и запуск надстройки

Рис. 9. Настройка гистограммы
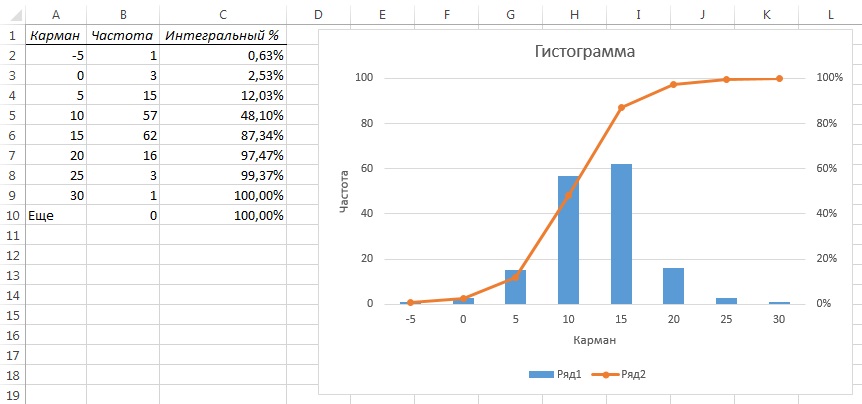
Рис. 10. Гистограмма с функцией распределения по диапазонам и интегральным процентом
Гистограмма
Полигон
Как и при построении гистограмм, величина исследуемой переменной откладывается вдоль горизонтальной оси. По вертикальной оси откладывается количество элементов в каждой группе, их относительная доля или процент. Процентный полигон представляет собой график, построенный путем соединения средних точек, соответствующих процентной доле каждой группы (рис. 11). Надстройка Анализ данных не умеет строить полигоны; с методом, использованным при построении графика на рис. 11 можно ознакомиться на соответствующем листе Excel-файла.

Рис. 11. Процентный полигон для пятилетней доходности
Полигон интегральных процентов, или кривая распределения, является графическим изображением распределения суммарных процентов (накопительным итогом).

Рис. 12. Полигон интегральных процентов
На рис. 12 изображены полигоны интегральных процентов (метод построения см. Excel-файл) на основе пятилетней среднегодовой доходности 158 фондов, ориентированных на быстрый рост капитала, и 101 фонда, ориентированного на медленный рост капитала. На оси X отложены средние значения диапазонов. Видно, что среднегодовая доходность 48,1% фондов, ориентированных на быстрый рост капитала, не превышает 10%, в то время как доля фондов, ориентированных на медленный рост капитала, в этом интервале равна 36,7%. Обратите внимание на то, что в интервале до 20% кривая распределения среднегодовой доходности фондов, ориентированных на быстрый рост капитала, расположена слева от кривой распределения доходности фондов, ориентированных на медленный рост капитала. В то же время количество фондов, ориентированных на быстрый и медленный рост капитала, доходность которых не превышает 20,0%, приблизительно одинаково.
Изображение двумерных числовых данных
Выше мы рассмотрели гистограммы, полигоны, кривые распределений и полигоны накопленных частот, представляющие собой удобные графические инструменты для анализа числовых одномерных данных. Для анализа двумерных числовых величин используется иной вид графического представления – диаграмма разброса. В программе Excel эта диаграмма называется точечной, а в научной литературе — корреляционной. Такие диаграммы оказываются полезными в разных областях деловой активности. Например, специалисты по маркетингу с помощью таких диаграмм могут исследовать эффективность рекламной кампании, сравнивая объемы недельных продаж и расходы на рекламу, а менеджеры по кадрам — изучать систему оплаты труда в компании, сравнивая трудовой стаж сотрудников и их текущую зарплату.
Используя диаграмму разброса, менеджер по логистике может анализировать вклад таможенного сбора в суммарные логистические затраты (рис. 13). Диаграммы разброса играют важную роль при изучении коэффициента корреляции, а также в регрессионном анализе.

Рис. 13. Корреляция таможенного сбора (как процентной доли таможенной стоимости, ось Y) и таможенной стоимости, ось Х
Для построения диаграммы разброса выберите два столбца и кликните на типе диаграммы Точечная (рис. 14). Обратите внимание на то, что Мастер диаграмм по умолчанию считает, что переменная X находится в первом столбце диапазона. Если данные на вашем листе расположены иначе, поменяйте столбцы местами.

Рис. 14. Построение точечной диаграммы
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 105–124
Использование Excel для расчета статистических характеристик случайной величины
Разделы: Математика
- Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
- применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.
- Сегодня на уроке мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
- Для начала вспомним:
– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)
– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)
– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).
– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).
– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).
- Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.
Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):
1. Занести данные в EXCEL, каждое число в отдельную ячейку.
| 23 | 25 | 24 | 25 | 30 | 24 | 30 | 26 | 28 | 26 |
| 32 | 33 | 31 | 31 | 25 | 33 | 25 | 29 | 30 | 28 |
| 23 | 30 | 29 | 24 | 33 | 30 | 30 | 28 | 26 | 25 |
| 26 | 29 | 27 | 29 | 26 | 28 | 27 | 26 | 29 | 28 |
| 29 | 30 | 27 | 30 | 28 | 32 | 28 | 26 | 30 | 26 |
| 31 | 27 | 30 | 27 | 33 | 28 | 26 | 30 | 31 | 29 |
| 27 | 30 | 30 | 29 | 27 | 26 | 28 | 31 | 29 | 28 |
| 33 | 27 | 30 | 33 | 26 | 31 | 34 | 28 | 32 | 22 |
| 29 | 30 | 27 | 29 | 34 | 29 | 32 | 29 | 29 | 30 |
| 29 | 29 | 36 | 29 | 29 | 34 | 23 | 28 | 24 | 28 |
2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем — статистические, в списке: МОДА
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Мо = 29 (чел) – Фирм у которых в штате 29 человек больше всего.
Используя тот же путь вычисляем медиану.
Вставка – Функция – Статистические – Медиана.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили Ме = 29 (чел) – среднее значение сотрудников в фирме.
Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.
Вставка – Функция – Статистические – МАКС.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наибольшее значение = 36.
Вставка – Функция – Статистические – МИН.
В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:
Нажимаем клавишу ОК. Получили наименьшее значение = 22.
36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.
Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения xi случайной величины меняются от 22 до 36 включительно шагом 1.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni |
Чтобы сосчитать частоту каждого значения воспользуемся
Вставка – Функция – Статистические – СЧЕТЕСЛИ.
В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22
Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.
| xi | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| ni | 1 | 3 | 4 | 5 | 11 | 9 | 13 | 18 | 16 | 6 | 4 | 6 | 3 | 0 | 1 |
Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические — СУММА). Должно получиться 100 (количество всех фирм).
Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)
Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.
Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).
Диаграмма – Стандартные – Круговая.
Диаграмма – Стандартные – Гистограмма.
4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.
Инструменты Excel для построения гистограмм, полигонов
В процедуре автоматически выполняются следующие вычисления:
выбирается число m интервалов группировки (7 £ m £ 20);
вычисляются середины интервалов группировки , , ;
для каждого интервала вычисляются частоты nj — количество выборочных значений, которые попали в j -й интервал;
для каждого интервала вычисляются накопленные частоты — количество выборочных значений, не превышающих верхней границы j -го интервала;
Строится гистограмма – график ступенчатой функции , , , D j = ( aj , bj ) , .
Для того чтобы вычислять накопленные частоты и отобразить гистограмму в листе в листе Excel , в окне процедуры следует пометить соответствующие поля.

Читайте также:


