Как сделать распределительный закон умножения
(a+b)c=ac+bc - \u043e\u0442\u043d\u043e\u0441\u0438\u0442\u0435\u043b\u044c\u043d\u043e \u0441\u043b\u043e\u0436\u0435\u043d\u0438\u044f
(a-b)c=ac-bc - \u043e\u0442\u043d\u043e\u0441\u0438\u0442\u0435\u043b\u044c\u043d\u043e \u0432\u044b\u0447\u0438\u0442\u0430\u043d\u0438\u044f
\u0421 \u041d\u043e\u0432\u044b\u043c \u0413\u043e\u0434\u043e\u043c )))">,\u0420\u0430\u0441\u043f\u0440\u0435\u0434\u0435\u043b\u0438\u0442\u0435\u043b\u044c\u043d\u044b\u0439 \u0437\u0430\u043a\u043e\u043d \u0443\u043c\u043d\u043e\u0436\u0435\u043d\u0438\u044f \u043e\u0442\u043d\u043e\u0441\u0438\u0442\u0435\u043b\u044c\u043d\u043e \u0441\u043b\u043e\u0436\u0435\u043d\u0438\u044f. \n
(a + b)\u00a0\u00b7 c = ac + bc \u00a0 \u0438\u043b\u0438 \u00a0 \u00a0\u0441\u00a0\u00b7\u00a0(a + b) = \u0441\u0430 + cb. \n
\u0427\u0442\u043e\u0431\u044b \u0441\u0443\u043c\u043c\u0443 \u0443\u043c\u043d\u043e\u0436\u0438\u0442\u044c \u043d\u0430 \u0447\u0438\u0441\u043b\u043e, \u043c\u043e\u0436\u043d\u043e \u0443\u043c\u043d\u043e\u0436\u0438\u0442\u044c \u043d\u0430 \u044d\u0442\u043e \u0447\u0438\u0441\u043b\u043e \u043a\u0430\u0436\u0434\u043e\u0435 \u0441\u043b\u0430\u0433\u0430\u0435\u043c\u043e\u0435 \u0438 \u043f\u043e\u043b\u0443\u0447\u0435\u043d\u043d\u044b\u0435 \u043f\u0440\u043e\u0438\u0437\u0432\u0435\u0434\u0435\u043d\u0438\u044f \u0441\u043b\u043e\u0436\u0438\u0442\u044c.
\u0420\u0430\u0441\u043f\u0440\u0435\u0434\u0435\u043b\u0438\u0442\u0435\u043b\u044c\u043d\u044b\u0439 \u0437\u0430\u043a\u043e\u043d \u0443\u043c\u043d\u043e\u0436\u0435\u043d\u0438\u044f \u043e\u0442\u043d\u043e\u0441\u0438\u0442\u0435\u043b\u044c\u043d\u043e \u0432\u044b\u0447\u0438\u0442\u0430\u043d\u0438\u044f. \n
(a - b)\u00a0\u00b7 c = ac - bc \u00a0 \u0438\u043b\u0438 \u00a0 \u00a0\u0441\u00a0\u00b7\u00a0(a - b) = \u0441\u0430 - cb. \n
\u0427\u0442\u043e\u0431\u044b \u0440\u0430\u0437\u043d\u043e\u0441\u0442\u044c \u0443\u043c\u043d\u043e\u0436\u0438\u0442\u044c \u043d\u0430 \u0447\u0438\u0441\u043b\u043e, \u043c\u043e\u0436\u043d\u043e \u0443\u043c\u043d\u043e\u0436\u0438\u0442\u044c \u043d\u0430 \u044d\u0442\u043e \u0447\u0438\u0441\u043b\u043e\n\u0443\u043c\u0435\u043d\u044c\u0448\u0430\u0435\u043c\u043e\u0435 \u0438 \u0432\u044b\u0447\u0438\u0442\u0430\u0435\u043c\u043e\u0435 \u043e\u0442\u0434\u0435\u043b\u044c\u043d\u043e \u0438 \u0438\u0437 \u043f\u0435\u0440\u0432\u043e\u0433\u043e \u043f\u0440\u043e\u0438\u0437\u0432\u0435\u0434\u0435\u043d\u0438\u044f \u0432\u044b\u0447\u0435\u0441\u0442\u044c\n\u0432\u0442\u043e\u0440\u043e\u0435.
">]" data-testid="answer_box_list">

Распределительный закон умножения относительно сложения.
(a + b) · c = ac + bc или с · (a + b) = са + cb.
Чтобы сумму умножить на число, можно умножить на это число каждое слагаемое и полученные произведения сложить.
Распределительный закон умножения относительно вычитания.
(a - b) · c = ac - bc или с · (a - b) = са - cb.
Чтобы разность умножить на число, можно умножить на это число уменьшаемое и вычитаемое отдельно и из первого произведения вычесть второе.


Новые вопросы в Математика
Детский сад привезли 3 коробки с зелёными кубиками и 5 коробок с красными. В каждой коробке по 10 кубиков. Задачу нужно решить двумя способами.
Помогите решить эту задачу как уровнение. легковой автомобиль со скоростью 80 км/ч, а из поселка Б Расстояние между поселками А и Б — 40 км. Из посе … лка А выеха одновременно грузовик со скоростью 60 км/ч. Через сколько часов легковая машина догонит грузовик? и, = 80 км/ч И, = 60 км/ч 4. еств. = ? ч . ГО А S = 40 км Б Б CS
В детский сад привезли 3 коробки с зелёными кубиками и 5 коробок с красными. В каждой коробке по 10 кубиков. Сколько всего кубиков привезли в детский … сад?
Математики - ленивые люди, поэтому они всё время создавали какие-то формулы, законы, обозначения. Их старания не прошли зря, теперь современный человек может легко решать уравнения и задачи. С лёгкостью доказывать теоремы по геометрии, и всё это благодаря формулам, обозначениям, свойствам!
Законы умножения и сложения
Их для умножения и сложения чисел всего три. Они очень полезны, благодаря им можно с лёгкостью решать большие уравнения. Каждый из них имеет свою формулу и название.
Первый закон умножения и сложения - сочетательный. Числа в таком случае группируют, зная, что сумма и произведение все равно не изменятся.
Второй закон умножения и сложения - переместительный. В этом случае числа перемещают так, как будет удобно, зная, что сумма и произведение также останутся теми же.
Третий, наиболее часто используемый, - распределительный закон. Его смысл в том, чтобы выполнять действия не отдельно для каждого числа, а умножать сразу на сумму. И наоборот, вносить множитель в скобки, умножая на каждое слагаемое. Это действительно удобно, и стоит научиться использовать этот закон!
Эти законы нельзя использовать для деления и вычитания, так как они могут изменить конечный результат.
Распределительный закон
Он очень удобен, ведь с его помощью можно умножать число на сумму без каких-либо трудностей! А всё потому, что распределять намного удобнее, чем просто умножать на каждый множитель.
Для наглядности можно рассмотреть пример, где он применяется при умножении и сложении.
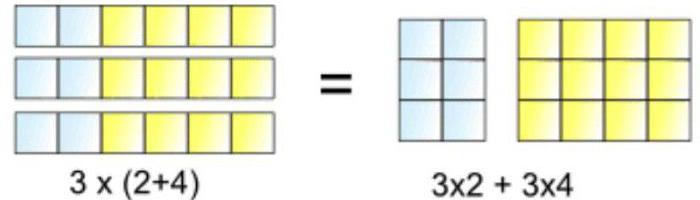
Дано выражение: 3 х 2 + 3 х 5.
Так выглядит обычное выражение. Если мы будем использовать распределительный закон, оно будет выглядеть так: 3 х (2 + 3) = 3 х 5 = 15.
Как видим, пользуясь этим удобным "средством", можно намного быстрее решать различные уравнения!
Всё на свете имеет своё название и формулировку, распределительный закон - не исключение! Стоит заучить его формулировку, чтобы с лёгкостью пользоваться им в любых условиях и при любых обстоятельствах. Стоит понять его действие!
Пример, где применяется распределительный закон умножения относительно сложения
Рассмотрим ещё один пример, где применим этот закон: 2 х 5 + 2 х 3 = 16.
Такое выражение было первоначально, а потом оно стало таким: 2 х (5 + 3) = 2 х 8 = 16.
Как видим, ответ не изменился, а выполнять действия стало намного легче! Это же прекрасно! Мы смогли облегчить себе жизнь!

Распределительный закон умножения относительно сложения очень полезен, поэтому им нужно пользоваться! Не стоит бояться пробовать что-то новое! Все свойства, теоремы и формулы есть в математике неспроста!
Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику

Тема. Распределительный закон умножения.
Цель: учить умножать целые числа, используя распределительный закон умножения; развитие ценностного отношения к знаниям как интеллектуальному ресурсу, обеспечивающему будущее человека, как результату кропотливого, но увлекательного учебного труда.
УУД: предметные: познакомиться с распределительным законом умножения целых чисел; познавательные: выделять характерные причинно-следственные связи регулятивные: учить ставить учебные цели и задачи; планировать свои действия в соответствии с поставленной задачей ; коммуникативные: аргументировать свою точку зрения; личностные: осмысление обсуждаемой проблемы, нахождение в ней личностного смысла; развитие рефлексивной способности .
Тип урока: изучение нового материала.
I. Оргмомент.
II. Проверка домашнего задания.
III. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
IV. Актуализация знаний.
V. Первичное усвоение новых знаний.
VI. Первичное закрепление.
VII. Итог урока.
VIII. Домашнее задание.
I. Оргмомент.
Проверка готовности класса к уроку, настраивание учащихся на работу.
II. Проверка домашнего задания.
П. 2.8 – повт., № 341 (в, м), № 343 (в).
в) х − (− 15 ) = 465;
х = 465 : (− 15 );
Ответ: х = −31.
м) (− 68 ) : х = − 4;
х = (− 68 ) : (− 4 );
Ответ: х = 17.
в) ( 24968 + 11648 ) : ( 768 − 1564 ) = − 46 ;

III. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
а) 13 + 59 + 47; б) −45 + 87 + 45; в) 2 ∙ (−34) ∙ (−5);
г) 69 ∙ 12 + 31 ∙ 12; д) 251 ∙ (−7) – 151 ∙(− 7);
Для решения второго задания, чем вы пользовались? Правильно, переместительным, сочетательным и распределительным законами. Если вы помните, скажите, как они звучат? Скажите, для чего нужны законы сложения и вычитания?
IV. Актуализация знаний.
Положительные числа – это…
Отрицательные числа – это…
Противоположные числа – это…
Модуль числа – это…
Любое положительное число всегда …
Любое отрицательное число всегда …
Из двух отрицательных чисел …
Чтобы сложить два числа с одинаковыми знаками, надо …
Чтобы сложить два числа с разными знаками надо …
Сумма противоположных чисел …
При умножении чисел с одинаковыми знаками получается …
При умножении чисел с разными знаками получается …
При умножении любого числа на нуль…
При делении чисел с одинаковыми знаками получается …
При делении чисел с разными знаками получается …
V. Первичное усвоение новых знаний.


VI. Первичное закрепление.
П. 2.9, № 344, № 345, № 346 (а, б, в, г, д, е), № 350 (1 стлб.), № 356 (1 стлб.)
№ 344. Запишите произведение в виде суммы (разности):
Распределительный закон: (а + b) · c = a · c + b · c.
б) 17 · ( 31 + 16 ) = 17 · 31 + 17 · 16 ; в) ( 28 + 37 ) · 56 = 28 · 56 + 37 · 56 ;
г) ( 72 + 98 ) · 12 = 72 · 12 + 98 · 12 ; д) ( 49 − 17 ) · 12 = 49 · 12 − 17 · 12 ;
е) 8 · ( 57 − 38 ) = 8 · 57 − 8 · 38 ; ж) 17 · ( 28 + 31 ) = 17 · 28 + 17 · 31 .
Распределительный закон : a · c + b · c = ( а + b) · c.
б) 57 · 38 + 57 · 64 = 57 · ( 38 + 64 ); в) 39 · 12 + 28 · 12 = 12 · ( 39 + 28 );
г) 73 · 57 + 79 · 57 = 57 · ( 73 + 79 ); д) 13 · 95 − 13 · 41 = 13 · ( 95 − 41 );
е) 27 · 48 − 19 · 48 = 48 · ( 27 − 19 ); ж) 54 · 88 − 54 · 87 = 54 · ( 88 − 87 ).
№ 346 (а, б, в, г, д, е).
а) 350 · 46 + 250 · 46 = 46 · ( 350 + 250 ) = 46 · 600 = 27600 ;
б) 728 · 49 − 528 · 49 = 49 · ( 728 − 528 ) = 49 · 200 = 9800 ;
в) 52 · 100 − 52 · 99 = 52 · ( 100 − 99 ) = 52 · 1 = 52 ;
г) 99 · 48 + 1 · 48 = ( 99 + 1 ) · 48 = 100 · 48 = 4800 ;
д) 4300 − 43 · 99 = 43 · 100 − 43 · 99 = 43 · ( 100 − 99 ) = 43 · 1 = 43 ;
№ 350 (1 стлб.).
б) 6 · ( 8 + (− 17 )) = 6 · 8 + 6 · (− 17 ); г) 16 · ( 8 − 17 ) = 16 · 8 + 16 · (− 17 );
е) ( 25 + 16 ) · (− 9 ) = 25 · (− 9 ) + 16 · (− 9 ); з) (− 15 − 42 ) · 13 = (− 15 ) · 13 + (− 42 ) · 13 .
№ 356 (1 стлб.).
б) 49 · 57 − 49 · 570 = 49 · ( 57 − 570 );
г) (− 53 ) · 48 − (− 53 ) · 59 = − 53 · ( 48 − 59 );
е) − 53 · 48 − 57 · 48 = 48 · ((− 53 ) − 57 ).
VII. Итог урока.
1. В процессе повторения теории (правил) в начале урока я принимал(а) активное участие
Да Нет Затрудняюсь ответить
2. Я выучил(а) правила, могу их применять
Да Нет Затрудняюсь ответить
3. Я решил(а) все задания правильно, я уверен(а)
Да Нет Затрудняюсь ответить
4. Урок мне понравился, всё понятно
Да Нет Затрудняюсь ответить
5. Могу оценить свою работу на уроке. Ставлю себе ___________________.
VIII. Домашнее задание.
П. 2.9 – читать, знать формулу, рассмотреть примеры, № 350 (2 стлб.), № 356 (2 стлб.), № 346 (и).
№ 350 (2 стлб.).
в) (− 7 ) · ((− 15 ) + (− 12 ) = (− 7 ) · (− 15 ) + (− 7 ) · (− 12 );
д) (− 17 ) · (− 15 − 12 ) = (− 17 ) · (− 15 ) + (− 17 ) · (− 12 );
ж) ( 45 − 17 ) · (− 11 ) = 45 · (− 11 ) + (− 17 ) · (− 11 );
и) (− 28 − 37 ) · (− 3 ) = (− 28 ) · (− 3 ) + (− 37 ) · (− 3 ).
№ 356 (2 стлб.).
в) 58 · 64 − 99 · 64 = 64 · ( 58 − 99 );
д) (− 45 ) · 12 + 95 · (− 45 ) = − 45 · ( 12 + 95 );
ж) − 45 · 13 − 45 · 27 = − 45 · ( 13 + 27 ).
и) 728 · 359 − 628 · 359 + 641 · 1000 = ( 728 − 628 ) · 359 + 641 · 1000 = 100 · 359 + 641 · 10 · 100 = 100 Х
Х ( 359 + 6410 ) = 100 · 6769 = 676900 .
1. В процессе повторения теории (правил) в начале урока я принимал(а) активное участие
Да Нет Затрудняюсь ответить
2. Я выучил(а) правила, могу их применять
Да Нет Затрудняюсь ответить
3. Я решил(а) все задания правильно, я уверен(а)
Да Нет Затрудняюсь ответить
4. Урок мне понравился, всё понятно
Да Нет Затрудняюсь ответить
5. Могу оценить свою работу на уроке. Ставлю себе ___________________.
1. В процессе повторения теории (правил) в начале урока я принимал(а) активное участие
Да Нет Затрудняюсь ответить
2. Я выучил(а) правила, могу их применять
Да Нет Затрудняюсь ответить
3. Я решил(а) все задания правильно, я уверен(а)
Да Нет Затрудняюсь ответить
4. Урок мне понравился, всё понятно
Да Нет Затрудняюсь ответить
5. Могу оценить свою работу на уроке. Ставлю себе ___________________.
1. В процессе повторения теории (правил) в начале урока я принимал(а) активное участие
Да Нет Затрудняюсь ответить
2. Я выучил(а) правила, могу их применять
Да Нет Затрудняюсь ответить
3. Я решил(а) все задания правильно, я уверен(а)
Да Нет Затрудняюсь ответить
4. Урок мне понравился, всё понятно
Да Нет Затрудняюсь ответить
5. Могу оценить свою работу на уроке. Ставлю себе ___________________.
1. В процессе повторения теории (правил) в начале урока я принимал(а) активное участие
Да Нет Затрудняюсь ответить
2. Я выучил(а) правила, могу их применять
Да Нет Затрудняюсь ответить
3. Я решил(а) все задания правильно, я уверен(а)
Да Нет Затрудняюсь ответить
4. Урок мне понравился, всё понятно
Да Нет Затрудняюсь ответить
5. Могу оценить свою работу на уроке. Ставлю себе ___________________.
1. В процессе повторения теории (правил) в начале урока я принимал(а) активное участие
Да Нет Затрудняюсь ответить
2. Я выучил(а) правила, могу их применять
Да Нет Затрудняюсь ответить
3. Я решил(а) все задания правильно, я уверен(а)
Да Нет Затрудняюсь ответить
4. Урок мне понравился, всё понятно
Да Нет Затрудняюсь ответить
5. Могу оценить свою работу на уроке. Ставлю себе ___________________.
Задача 1. На скотном дворе гуляли гуси и поросята. Мальчик сосчитал количество голов, их оказалось 30, затем он сосчитал количество ног, их оказалось 84. Сколько гусей и сколько поросят было на школьном дворе?
1) Представьте, что все поросята подняли по две ноги вверх
2) на земле осталось стоять 30 · 2 = 60 ног
3) подняли вверх 84 − 60 = 24 ноги
4) подняли 24 : 2 = 12 поросят
5) 30 − 12 = 18 гусей
Ответ: 12 поросят и 18 гусей.
Задача 2. Имеются двое песочных часов: на 3 минуты и на 7 минут. Яйцо варится 11 минут. Как отмерить это время при помощи имеющихся часов?
Перевернуть обои часы. Когда пройдёт 3 минуты в семиминутных часах останется 4 минуты. Поставьте яйца в это время вариться. Когда 4 минуты закончатся, перевернуть семиминутные часы обратно 4 + 7 + 11 мин.
Задача 1. На скотном дворе гуляли гуси и поросята. Мальчик сосчитал количество голов, их оказалось 30, затем он сосчитал количество ног, их оказалось 84. Сколько гусей и сколько поросят было на школьном дворе?
Задача 2. Имеются двое песочных часов: на 3 минуты и на 7 минут. Яйцо варится 11 минут. Как отмерить это время при помощи имеющихся часов?
Задача 1. На скотном дворе гуляли гуси и поросята. Мальчик сосчитал количество голов, их оказалось 30, затем он сосчитал количество ног, их оказалось 84. Сколько гусей и сколько поросят было на школьном дворе?
Задача 2. Имеются двое песочных часов: на 3 минуты и на 7 минут. Яйцо варится 11 минут. Как отмерить это время при помощи имеющихся часов?
Задача 1. На скотном дворе гуляли гуси и поросята. Мальчик сосчитал количество голов, их оказалось 30, затем он сосчитал количество ног, их оказалось 84. Сколько гусей и сколько поросят было на школьном дворе?
Задача 2. Имеются двое песочных часов: на 3 минуты и на 7 минут. Яйцо варится 11 минут. Как отмерить это время при помощи имеющихся часов?
Задача 1. На скотном дворе гуляли гуси и поросята. Мальчик сосчитал количество голов, их оказалось 30, затем он сосчитал количество ног, их оказалось 84. Сколько гусей и сколько поросят было на школьном дворе?
Задача 2. Имеются двое песочных часов: на 3 минуты и на 7 минут. Яйцо варится 11 минут. Как отмерить это время при помощи имеющихся часов?
Задача 1. На скотном дворе гуляли гуси и поросята. Мальчик сосчитал количество голов, их оказалось 30, затем он сосчитал количество ног, их оказалось 84. Сколько гусей и сколько поросят было на школьном дворе?
Задача 2. Имеются двое песочных часов: на 3 минуты и на 7 минут. Яйцо варится 11 минут. Как отмерить это время при помощи имеющихся часов?
Задача 1. На скотном дворе гуляли гуси и поросята. Мальчик сосчитал количество голов, их оказалось 30, затем он сосчитал количество ног, их оказалось 84. Сколько гусей и сколько поросят было на школьном дворе?
Задача 2. Имеются двое песочных часов: на 3 минуты и на 7 минут. Яйцо варится 11 минут. Как отмерить это время при помощи имеющихся часов?
Задача 1. На скотном дворе гуляли гуси и поросята. Мальчик сосчитал количество голов, их оказалось 30, затем он сосчитал количество ног, их оказалось 84. Сколько гусей и сколько поросят было на школьном дворе?
Задача 2. Имеются двое песочных часов: на 3 минуты и на 7 минут. Яйцо варится 11 минут. Как отмерить это время при помощи имеющихся часов?
Тип урока: урок изучения и первичного закрепления новых знаний.
Цель: способствовать созданию условий для самостоятельного открытия учащимися распределительного закона умножения относительно сложения.
-
Формировать представление о формулировке и записи распределительного закона умножения относительно сложения через формулу; умение по применению на практике распределительного закона умножения относительно сложения и записи его в общем виде, используя буквы.
- Развивать математическую речь, логическое мышление, умения сравнивать, наблюдать, анализировать, выдвигать гипотезы, размышлять, отыскивать разные решения, классифицировать, обобщать, формулировать выводы и отстаивать свою точку зрения.
- Продолжить работу по воспитанию любви к предмету, любознательности, чувства сопереживания и уважительного отношения к мнению одноклассников, культуры общения.
Методы и приёмы: словесный, наглядный, исследовательский, проблемно-поисковый.
Формы организации познавательной деятельности: индивидуальная, групповая, работа в парах.
Средства обучения: учебник, карточки, пословица, мультимедийная доска (проектор), смайлики.
- Аргинская И. И., Ивановская Е. И., Кормишина С.Н. Математика: Учебник для 3 класса: В 2 частях. - Самара: Издательство “Учебная литература”:Издательский дом “Фёдоров”,2008. Часть I.
- И.И.Аргинская “Сборник заданий по математике для самостоятельных, проверочных и контрольных работ в начальной школе”, издательство “Учебная литература”, 2006г.
| Этапы урока | Ход урока |
| 1. Психологический настрой детей на урок | Учитель: |
- Сегодня очень хороший солнечный день.
- Давайте мы улыбнёмся друг другу.
- Пусть наш урок будет интересным и даст нам возможность открыть новые знания.
- Желаю всем нам успеха! В путь!
- Один мудрец однажды сказал: “Не для школы, а для жизни мы учимся!”
- В чём заключается смысл данной пословицы? (Слайд 1)
- Предлагаю решить логические задачи в группах. (деление класса на 3 группы)
1 группа. Валя и Наташа учатся в одном классе.“Я всегда захожу в четвёртый кабинет от начала коридора”, - сказала Наташа. “А я захожу в четвёртый кабинет от его конца”, - сказала Валя. Ск. кл. комнат на этом этаже? (7 комнат.)
2 группа. Васиного отца зовут Иван Николаевич, а дедушку – Семён Петрович. Каково отчество Васиной мамы? (Семёновна)
3 группа. Ребята пилят брёвна на метровые куски. Отпиливание одного такого куска занимает одну минуту. За сколько минут они распилят бревно длиной 5 метров? (за 4 минуты)
- Слово предоставляется представителям от каждой группы.
(выслушивается и оценивается работа всех групп)
- Молодцы! Все хорошо потрудились!.
- Посмотрите на следующее задание.
- Что можете сказать про эту запись? 20, 12, 11. (Слайд 2)
- Это числа. Их три. Все они натуральные.
Здесь есть чётные и нечётные числа. Они двузначные. Числа записаны в порядке убывания.
- Какое задание вы бы предложили своим одноклассникам, используя данные числа?
- Найти лишнее число.
- Разделить числа на группы и дополнить эти группы своими числами.
- Расположить числа в порядке возрастания.
- Найти сумму (разность) этих чисел.
- Представить числа в виде суммы разрядных слагаемых. . и т.д.
- А кто из вас внимательный? Есть ли какая-то связь этих чисел с сегодняшним днём?
- Это дата: 20 декабря 2011 год.
- А сейчас проведём зарядку для ума – математический диктант. В тетрадях записываем только значение выражений. (диктант)
- Обменяемся тетрадями и проверим друг друга по образцу. (Слайд №3.)
15, 56, 54, 2, 49, 74, 79, 6, 100, 66
- Встаньте те ребята, которые не допустили ни одной ошибки. - Молодцы.
- Какие знания вам были нужны при выполнении диктанта?
- Знание компонентов сложения, вычитания, умножения и деления, таблицы умножения, деления, сложения, вычитания.Умение понимать задание и правильно выполнять действия с числами. . и т.д.
Учитель: - Молодцы! Спасибо за старание.
- Представьте три наименьших числа, из записанных нами чисел в виде суммы одинаковых слагаемых. Запишите результаты в тетради.
- 2=1+1
- 6=3+3
- 6=2+2+2
- 6=1+1+1+1+1+1
- 15=5+5+5
- 15=3+3+3+3+3
- 15=1+1+1+1+1+1+1+1+1+1+1+1+1+1+1
- Представьте каждое из этих чисел в виде произведения двух множителей.
- 2=1*2
- 2=2*1
- 6=2*3
- 6=3*2
- 6=6*1
- 6=1*6
- 15=5*3
- 15=3*5
- 15=15*1
- 15=1*15
- Как вы думаете, для чего нам нужны знания таблицы умножения?
- Когда ею можно заменить сложение?
(о связи сложения с умножением)
- Да, сегодня нам эти знания очень пригодятся.
- (3+5)*3.
- 3*3+5*3
- (4+2)*2.
- 4*2+2*2
- Сравните выражения каждой пары.
- Чем похожи выражения каждой пары?
- Использованы одни и те же числа.
- И там, и там встречается умножение и сложение.
- Выражение решается в несколько действий.
- Чем они отличаются?
- Наличием скобок. Количеством действий.
- Попробуйте, опираясь на свои знания, найти значения выражений.
- Что интересного заметили?
- В чём особенность получившихся значений?
Высказывания детей:
- Попытайтесь сформулировать вывод, почему значения записанных выражений одинаковы?
- Вывод: в первой паре мы сумму чисел умножали на число, во второй паре мы находили значение суммы, где каждое слагаемое дано в виде произведения чисел. Найдя значения выражений, мы увидели, что они равны между собой.
-Давайте сформулируем наше новое знание.
- Вывод: при умножении суммы на число значение выражения не изменится, если умножить на это число каждое слагаемое и полученные результаты сложить.
- Где мы можем проверить нашу гипотезу?
- Откройте учебник на стр.93. (Слайд 5)
- Прочитаем утверждение, которое здесь записано.
- Сравните данное утверждение с тем, которое мы сделали сами. (Высказывания детей)
- Какое открытие сделали?
Высказывания детей :
- Вы думаете, что всё самое интересное уже позади?
- Нет, всё ещё впереди.
- Выполним пункт 3, №168. Работать будем в парах.
(Составь ещё три пары похожих выражений и найди их значение)
- Проверим варианты решений на доске.
- С каким свойством умножения познакомились?
- Как звучит новое математическое свойство?
(воспроизводят переместительное свойство умножения относительно сложения)
- Какова наша задача на уроке?
- Применять новые знания при решении задач и примеров.
- Предлагаю записать формулу в общем виде, используя буквы а,в,с, опираясь на выполненные выражения в предыдущих заданиях.
- (а+в)*с=а*с+в*с (Слайд 7)
- Сравните нашу формулу с формулой в учебнике на стр.93, пункт 6, №168.
- Почему разные записи?
Вам предлагается решить 2 выражения по выбору.
- При выполнении каких заданий мы можем применить этот закон?
- При решении задач, примеров, .
- Как называется фигура, которая изображена на стр.95, №171?
- Можем ли мы найти площадь этой фигуры?
- Как это сделать?
- Разбить фигуру на прямоугольники, найти их площади и полученные площади сложить.
- Представить визуально прямоугольники.
2). Нахождение площади фигуры.
-Сам-но найдите S фигуры любым способом.
- 1 способ: 6*6=36(см 2 )
- 2 способ: 6*3+4*3+2*3=36(см 2 )
- 3 способ: 9*4=36(см 2 )
- 4 способ: 3*2+6*2+9*2=36(см 2 )
(После выполнения №171 проводится проверка, во время которой выявляются рациональные способы нахождения площади данной фигуры).
- Какие способы нахождения площади на ваш взгляд самые рациональные? Почему?
- Требуют меньше всего выполнения действий и вычислений.
- Учебник стр.94 №170. Прочитайте 1, а затем 2 задачи. (Слайд 10)
- Предлагаю составить краткую запись к задаче, пользуясь таблицей.
- Сравните задачи. Чем они похожи?
Высказывания детей : (По содержанию и сюжету. Встречаются одинаковые числа.)
Учитель: - В чём их основное различие?
- Количество детских и женских платье в 1 задаче различно, а во 2-й - одинаково.
- Реши обе задачи по действиям или выражением.
- Для какой задачи можно составить более короткое числовое выражение?
- Запись 3*5+2*5 можно заменить записью (3+2)*5
Учитель: - Какое свойство умножения применяется при его решении?
(распределительное свойство умножения относительно сложения)
- Я узнал (а) .
- Я повторил (а) .
- Я научился (лась) .
- Какое вы сегодня сделали открытие?
- Как формулируется распределительный закон умножения относительно сложения?
- Кому вы скажите спасибо за работу на уроке?
- У каждого из вас, на парте, лежит смайлик. Выберите тот смайлик, который соответствует вашему настроению от сегодняшнего урока.
- Вспомните слова мудреца, сказанные в начале урока: “Не для школы, а для жизни мы учимся!”
- Как вы их понимаете сейчас?
-А теперь крепко потрите свои ладошки, так, чтобы стало жарко. Быстро передайте тепло другу, соединив свои ладошки с ладошками соседа.
Сумма не меняется от перестановки её слагаемых: a + b = b + a.
2. Сочетательный закон
Сумма не зависит от группировки её слагаемых: (a + b) + c = a + (b + c) = a + b + c
3. Свойство нуля
Сумма нуля и любого числа равна этому числу: 0 + a = a
4. Свойство противоположных чисел
Сумма противоположных чисел равна нулю: a + (-a)=0
1. Переместительный закон
Произведение не меняется от перестановки его сомножителей: ab = ba.
2. Сочетательный закон
Произведение не зависит от группировки его сомножителей: (ab)c = a(bc) = abc
3. Распределительный закон
Произведение числа и суммы равно сумме произведений числа на слагаемые суммы: $$a(b +c )= ab + ac$$
4. Свойство единицы
Произведение единицы и любого числа равно этому числу: $1 \cdot a = a$
5. Свойство нуля
Произведение нуля и любого числа равно нулю: $0 \cdot a = 0$
6. Свойство обратных чисел
Произведение обратных чисел равно единице: $a \cdot a \frac 1a = 1 (a \neq 0)$
Применение переместительных и сочетательных законов сложения и умножения к числовым выражениям значительно облегчает вычисления.
Пример 1. Найдите значение выражения, выбирая удобный порядок вычислений
$(3\frac + 4\frac ) + (2\frac - 1\frac ) + \frac 23 \cdot 0,2 \cdot 0,8 \cdot 5 \cdot 1,25 =$
$= (3\frac + 2\frac ) + (4\frac - 1\frac ) + \frac 23 \cdot (0,2 \cdot 0,5) \cdot (0,8 \cdot 1,25) =$
$= (3 + 2 \frac + 4 - 1) + \frac + \frac 23 \cdot 1 \cdot 1 = 9 + (\frac 13 + \frac 23) = 10$
Пример 2. Вычислите удобным способом:
$(74,7 \cdot \frac + (-105,3) \cdot 2 \frac 37 - (-105,3) \cdot \frac - 2 \frac \cdot 74,7) : 10 =$
$( \frac (74,7 + 105,3) - 2 \frac 37 (105,3 + 74,7)) : 10 = ( \frac - 2 \frac 37 ) \cdot (74 + 105 + 1) : 10 = $
$( \frac - \frac - 2) \cdot (180 : 10) = \frac \cdot 18 = \frac \cdot 6 = -7 \cdot 6 = 42$
п.2. Приведение подобных слагаемых
Применение законов сложения и умножения к выражениям с переменными также даёт возможность их упростить, прежде всего, с помощью приведения подобных слагаемых.
Подобные слагаемые – это слагаемые в выражении с переменными, имеющие одинаковую буквенную часть (любое буквенное выражение); числа без буквенной части также считаются подобными слагаемыми.
Заметим, что в выражении 3ab+2ba слагаемые подобны, т.к. 2ba=2ab по переместительному закону умножения.
Получаем следующий алгоритм.
Алгоритм приведения подобных слагаемых
1. Провести перестановку слагаемых так, чтобы подобные слагаемые оказались рядом, сгруппировать их с помощью скобок.
2. Вынести за скобки буквенную часть подобных слагаемых.
3. Вычислить значение числового выражения в скобках. Это – новый числовой коэффициент.
4. Заменить подобные слагаемые в выражении полученным результатом.
Пример 3. Упростите выражение:
$3(a + 4b - 1) - 4(2a - b + 4) + a = 3a + 3 \cdot 4b - 3 - 4 \cdot 2a + 4b - 16 + a=$
$= (3a - 8a + a) + (12b + 4b) - (3 + 16) = (3 - 8 + 1)a + (12 + 4)b - 19=$
Читайте также:


