Как сделать потенциальную диаграмму для контура
Совокупность радиус-векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения, токи и т. д., называется векторной диаграммой. Векторные диаграммы наглядно иллюстрируют ход решения задачи. При точном построении векторов можно непосредственно из диаграммы определить амплитуды и фазы искомых величин. Приближенное (качественное) построение диаграмм при аналитическом решении служит надежным контролем корректности хода решения и позволяет легко определить квадрант, в котором находятся определяемые векторы.
При построении векторных диаграмм для цепей с последовательным соединением элементов за базовый (отправной) вектор следует принимать вектор тока (см. лекцию № 8), а к нему под соответствующими углами подстраивать векторы напряжений на отдельных элементах. Для цепей с параллельным соединением элементов за базовый (отправной) вектор следует принять вектор напряжения (см. лекцию № 8), ориентируя относительно него векторы токов в параллельных ветвях.
Для наглядного определения величины и фазы напряжения между различными точками электрической цепи удобно использовать топографические диаграммы. Они представляют собой соединенные соответственно схеме электрической цепи точки на комплексной плоскости, отображающие их потенциалы. На топографической диаграмме, представляющей собой в принципе векторную диаграмму, порядок расположения векторов напряжений строго соответствует порядку расположения элементов в схеме, а вектор падения напряжения на каждом последующем элементе примыкает к концу вектора напряжения на каждом предыдущем элементе.
В качестве примера построим векторную диаграмму токов, а также топографическую диаграмму потенциалов для схемы, расчет которой был приведен в лекции № 5 (см. рис. 1).
При данных параметрах и заданном напряжении на входе схемы найденные значения токов (см. лекцию № 5) равны: ; ; .
При построении векторной диаграммы зададимся масштабами токов и напряжений (см. рис. 2). Векторную диаграмму можно строить, имея запись комплекса в показательной форме, т.е. по значениям модуля и фазы . Однако на практике удобнее проводить построения, используя алгебраическую форму записи, поскольку при этом вещественная и мнимая составляющие комплексной величины непосредственно откладываются на соответствующих осях комплексной плоскости, определяя положение точки на ней.
Построение векторной диаграммы токов осуществляется непосредственно на основании известных значений их комплексов. Для построения топографической диаграммы предварительно осуществим расчет комплексных потенциалов (другой вариант построения топографической диаграммы предполагает расчет комплексов напряжений на элементах цепи с последующим суммированием векторов напряжений вдоль контура непосредственно на комплексной плоскости).
При построении топографической диаграммы обход контуров можно производить по направлению тока или против. Чаще используют второй вариант.
В этом случае с учетом того, что в электротехнике принято, что ток течет от большего потенциала к меньшему, потенциал искомой точки равен потенциалу предыдущей плюс падение напряжения на элементе между этими точками. Если на пути обхода встречается источник ЭДС, то потенциал искомой точки будет равен потенциалу предыдущей плюс величина этой ЭДС, если направление обхода совпадает с направлением ЭДС, и минус величина ЭДС, если не совпадает. Это вытекает из того, что напряжение на источнике ЭДС имеет направление, противоположное ЭДС.
Обозначив на схеме по рис. 1 точки между элементами цепи e и a и приняв потенциал точки а за нуль( ), определим потенциалы этих точек:
Таким образом, в результате проведенных вычислений получено, что . Но разность потенциалов точек е и а равно напряжению U, приложенному к цепи, а оно равно 120 В. Таким образом, второй закон Кирхгофа выполняется, а следовательно, вычисления выполнены верно. В соответствии с полученными результатами строится топографическая диаграмма на рис. 2. Следует обратить внимание на ориентацию векторов, составляющих топографическую диаграмму, относительно векторов тока: для резистивных элементов соответствующие векторы параллельны, для индуктивного и емкостных – ортогональны.
В заключение заметим, что векторы напряжений ориентированы относительно точек топографической диаграммы противоположно положительным направлениям напряжений относительно соответствующих точек электрической цепи. В этой связи допускается не указывать на топографической диаграмме направления векторов напряжений.
Потенциальная диаграмма
Потенциальная диаграмма применяется при анализе цепей постоянного тока. Она представляет собой график распределения потенциала вдоль участка цепи или контура, при этом по оси абсцисс откладываются сопротивления резистивных элементов, встречающихся на пути обхода ветви или контура, а по оси ординат – потенциалы соответствующих точек. Таким образом, каждой точке рассматриваемого участка или контура соответствует точка на потенциальной диаграмме.
Рассмотрим построение потенциальной диаграммы на примере схемы на рис. 3.
При параметрах схемы ; ; ; ; и токи в ветвях схемы равны: ; ; .
Построим потенциальную диаграмму для контура abcda.
Для выбора масштаба по оси абсцисс просуммируем сопротивления резисторов вдоль рассматриваемого контура: после чего определим потенциалы точек контура относительно потенциала произвольно выбранной точки a, потенциал которой принят за нуль:
Таким образом, координаты точек потенциальной диаграммы: а(0;0);b(4;-20); c(4;17); d(7;2). С учетом выбранных масштабов на рис. 4 построена потенциальная диаграмма для выбранного контура.
Преобразование линейных электрических схем
Для упрощения расчета и повышения наглядности анализа сложных электрических цепей во многих случаях рационально подвергнуть их предварительному преобразованию. Очевидно, что преобразование должно приводить к упрощению исходной схемы за счет уменьшения числа ее ветвей и (или) узлов. Такое преобразование называется целесообразным. При этом при любых способах преобразований должно выполняться условие неизменности токов в ветвях участков схемы, не затронутых этими преобразованиями. Из последнего вытекает, что, если преобразованию подвергаются участки цепи, не содержащие источников энергии, то мощности в исходной и эквивалентной схемах одинаковы. Если в преобразуемые участки входят источники энергии, то в общем случае мощности в исходной и преобразованной цепях будут различны.
Рассмотрим наиболее важные случаи преобразования электрических цепей.
1. Преобразование последовательно соединенных элементов
Рассмотрим участок цепи на рис. 5,а. При расчете внешней по отношению к этому участку цепи данную ветвь можно свести к виду на рис. 5,б, где
При этом при вычислении эквивалентной ЭДС k-я ЭДС берется со знаком “+”, если ее направление совпадает с направлением эквивалентной ЭДС, и “-”, если не совпадает.
2. Преобразование параллельно соединенных ветвей
Пусть имеем схему на рис. 6,а.
Согласно закону Ома для участка цепи с источником ЭДС
| ; | (3) |
| , | (4) |
причем со знаком “+” в (4) записываются ЭДС и ток , если они направлены к тому же узлу, что и ЭДС ; в противном случае они записываются со знаком “-”.
3. Взаимные преобразования “треугольник-звезда”
В ряде случаев могут встретиться схемы, соединения в которых нельзя отнести ни к последовательному, ни к параллельному типу (см. рис. 7). В таких случаях преобразования носят более сложный характер: преобразование треугольника в звезду и наоборот.
Преобразовать треугольник в звезду – значит заменить три сопротивления, соединенных в треугольник между какими-то тремя узлами, другими тремя сопротивлениями, соединенными в звезду между теми же точками. При этом на участках схемы, не затронутых этими преобразованиями, токи должны остаться неизменными.
Без вывода запишем формулы эквивалентных преобразований
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш.шк., 1978. –528с.
Контрольные вопросы и задачи
- Что представляют собой векторные диаграммы?
- Что такое топографические диаграммы, для чего они служат?
- В чем сходство и различие топографической и потенциальной диаграмм?
- Какой практический смысл преобразований электрических цепей?
- В чем заключается принцип эквивалентности преобразований?
- Построить потенциальные диаграммы для левого и внешнего контуров цепи рис.3.
Участок ветви, содержащий один или несколько источников энергии, является активным.
Положительные направления тока и напряжения указаны стрелкой.
Определим потенциалы точек c, d, e, b, предположив, что известен потенциал точки a-ja.
Для правильного выбора знаков следует помнить, что:
1) ток в сопротивлении всегда направлен от более высокого потенциала к более низкому, т.е. потенциал падает по направлению тока.
3) напряжение U=Uac положительно, когда потенциал точки а выше, чем потенциал точки с.
При обозначении напряжения (разности потенциалов) на схемах посредством стрелки она ставится в направлении от точки высшего потенциала к точке низшего потенциала.
На участке cd э.д.с. E1 действует в сторону повышения потенциала, следовательно:
Чтобы наглядно оценить распределение потенциала вдоль участка цепи, полезно построить потенциальную диаграмму, которая представляет график изменения потенциала вдоль участка цепи или замкнутого контура.
По оси абсцисс графика откладываются потенциалы точек, а по оси ординат – сопротивления отдельных участков цепи. Для участка цепи рис. 16 распределение потенциала построено на рис. 17.
Рис. 16. Потенциальная диаграмма участка цепи.
Потенциальная диаграмма рис. 16 построена, начиная с точки a, которая условно принята за начало отсчета. Потенциал ja принят равным нулю.
Точка цепи, потенциал которой условно принимается равным нулю, называется базисной.
Если в условии задачи не оговорено, какая точка является базисной, то можно потенциал любой точки условно приравнивать к нулю. Тогда потенциалы всех остальных точек будут определяться относительно выбранного базиса.
Обобщенный закон Ома.
Закон Ома выражаемый формулой , определяет зависимость между током и напряжением на пассивном участке электрической цепи.
Определим зависимость между током, напряжением и э.д.с. на активном участке (рис. 16).
Из формулы 15 следует:
На положительное напряжение на участке a – b Uab=ja -jb
Формула (18) выражает обобщенный закон Ома, или закон Ома для участка, содержащего э.д.с.
Закон Ома применяется для участка ветви и для одноконтурной замкнутой схемы.
Пример № 1. Построения потенциальной диаграммы:
Построить потенциальную диаграмму для одноконтурной схемы:
Решение: 1. перерисуем заданный контур, вынося внутренние сопротивления э.д.с. (r1- r4) за их пределы; обозначим точки контура.
2. Выберем положительное направление тока I, определим его значение используя обобщенный закон Ома:
3. За базисную точку примем точку a. Найдем потенциалы остальных точек:
4. В системе координат строим потенциальную диаграмму:
1. Метод контурных токов.
Метод контурных токов.
Метод контурных токов – один из основных и широко применяемых на практике методов. Он заключается в определении по второму закону Кирхгофа контурных токов. Для каждого контура цепи задают ток, который остается неизменным. В цепи протекает столько контурных токов, сколько независимых контуров в ней содержится. Направление контурного тока выбирают произвольно.
Контурные токи, проходя через узел, остаются непрерывными. Следовательно, первый закон Кирхгофа выполняется автоматически. Уравнения с контурными токами записываются только для второго закона Кирхгофа. Число уравнений, составленных по методу контурных токов, меньше чем по методу законов Кирхгофа.
Рис.28. Иллюстрация к методу контурных токов.
На рис.28 показана цепь с двумя независимыми контурами, следовательно, и с двумя контурными токами I11 и I22.
Токи в ветвях I1 и I2 равны контурным токам:
Ток I3 равен сумме этих двух контурных токов:
По второму закону Кирхгофа для первого контура цепи:
r11 – сумма всех сопротивлений, входящих в контур I, называется собственным сопротивлением контура.
r12 – сопротивление ветви, общей для контура I и II;
E11 называется контурной э.д.с.
Аналогично для второго контура рис.28.
Уравнения, составленные по методу контурных токов, всегда записывают в виде системы. Для схемы рис.28:
В результате решения системы находят контурные токи, а затем токи ветвей.
Если заданная электрическая цепь содержит n независимых контуров, то на основании второго закона Кирхгофа получается n контурных уравнений:
Число уравнений, составляемых по методу контурных токов, определяется по формуле:
где Nb – число ветвей электрической цепи;
Nи.т. – число идеальных источников тока.
Если в цепи отсутствуют источники тока, число уравнений равно числу контурных токов и, соответственно, числу независимых контуров рассматриваемой электрической цепи.
Пример.
Решим пример, используя метод контурных токов.
(Для схемы рис.1 составить уравнения по законам Кирхгофа и определить неизвестные точки.)
Цепь содержит три контура, через которые протекают контурные токи.
При наличии источников тока надо так направлять контурные токи, чтобы они протекали через данные источники. Но через один источник тока не может протекать два контурных тока.
На рис.1 обозначены положительные направления контурных токов. Очевидно, что I11=J1; I22=-J2
Контурный ток I33 – неизвестен, для него составляем уравнение:
В результате решения определяем I33=16,25 мА
4. Применение законов Кирхгофа для расчета электрических цепей.
1 закон: алгебраическая сумма токов в узле равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:

2 закон: алгебраическая сумма падений напряжений в замкнутом контуре равна алгебраической сумме ЭДС этого контура. . . 2 закон не записывается для контуров содержащих источники тока. Напряжение и ЭДС совпадающие с направлением обхода контура записываем со знаком (+), несовпадающие со знаком (-)
Метод наложения основан на принципе наложения: ток в любой ветви электрической цепи от действия нескольких источников равен алгебраической сумме токов от действия каждого источника в отдельности.
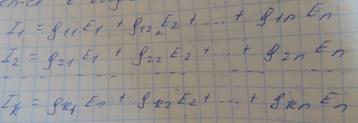
Где коэффициенты g11,g22… называются входными проводимостями, а g12, g13… наз-ся взаимными проводимостями.
Отношение контурного тока к ЭДС, действующей в том же контуре, при отсутствии независимых источников во всех остальных контурах называется входной проводимостью.
Отношение контурного тока к ЭДС, действующей в другом контуре, при отсутствии независимых источников во всех остальных контурах называется передаточной (взаимной) проводимостью.
Отношение напряжения в узле к току, заданному в том же узле, при отсутствии в схеме других независимых источников называется входным сопротивлением эл-кой цепи.
Отношение напряжения в узле к току, заданному в другом узле, при отсутствии в схеме других источников называется передаточным (взаимным) сопротивлением узлов.
8. Метод узловых потенциалов (напряжений).
Метод узловых напряжений заключается в том , что на основании первого закона Кирхгофа определяются потенциалы в узлах эл-кой цепи относительно базисного узла. Эти разности потенциалов называются узловыми напряжениями.
Узловое напряжение- это напряжение в данном узле относительно базисного.
Напряжение на какой-либо ветви равно разности узловых напряжений; произведение же этого напряжения на комплексную проводимость данной ветви равно току в этой ветви. Т.о., зная узловые напряжения в электрической цепи , можно найти токи в ветвях.
Если принять потенциал базисного узла равным нулю, то напряжение между остальными узлами и базисным узлом будут равны также потенциалам этих узлов. Поэтому данный метод называется также методом узловых потенциалов.
Собственная проводимость равняется сумме проводимостей ветвей сходящихся в данном узле. Величина положительная.
9.Применение метода узловых потенциалов при наличии в цепи идеальных источников эдс.

За базисный принимается один из узлов между которыми находится идеальный источник ЭДС.
В ветви с идеальным источником ток находится по первому закону Кирхгофа:

Суть метода преобразований состоит в упрощении цепи и, как следствие, ее расчета.
1)Преобразуем схему к простой (склеиваем все r и Е)
2)Треугольники преобразуем в звёзды
3)Находим ток в ветви
4)Раскрываем ветвь и считаем всё по току который нашли
Ток протекает везде одинаковый.
Напряжение равно сумме всех напряжений.
При параллельном соединении напряжение везде одинаковое.
G0=1/R1 [см] – проводимость величина обратная сопротивлению.(сименс)
12) Преобразование треугольников в эквивалентную звезду-называется такая замена части цепи, соединенной по схеме треугольником цепью соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи сохраняются неизменной.
 |

13)Эквивалентные преобразования активных соединений звездой и треугольником.
Преобразование треугольников в эквивалентную звезду-называется такая замена части цепи, соединенной по схеме треугольником цепью соединенной по схеме звезды, при которой токи и напряжения в остальной части цепи сохраняются неизменной.
 |
Преобразуем ЭДС в источник тока по формулам I=E/rвн, g=1/rвн

14)Метод основан на методе наложения и используется в том случае, если схема содержит один источник.
В этом методе произвольно задается ток самой дальней ветви от источника. По закону Ома и законам Кирхгофа определяют расчетные значения ЭДС источника. Вычисляя отношение расчетного значения ЭДС к заданному значению, получают коэффициент пропорциональности:
15)Баланс мощностей в цепи постоянного тока.
Из закона сохранения энергии следует, что вся мощность поступающая в цепь от источников энергии в любой момент времени равна всей мощности потребляемой приемниками данной цепи.
– мощность потребителей которыми в цепи постоянного тока являются резисторы.
Т.к. ток входит в выражение в квадрате, то независимо от его направления мощность потребителя всегда положительна.
Мощность источника бывает как положительной так и отрицательной.
РЕ=IE, где I – ток ветви с источником:
Мощность источника тока определяется по формуле:
PI=IU, где I- значение тока источника, U–напряжение на его зажимах.
Если ток Iи напряжение Uдействуют так, как показано на рисунке, то мощность в источнике тока положительная в противном случае отрицательная.
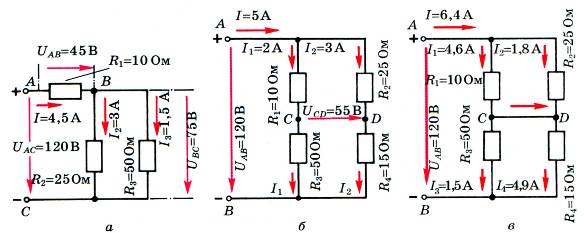
Рис. 1.
Тогда φА = 120 В. Когда движение направлено от точки А к точке В, потенциал будет уменьшаться на значение падения напряжения на сопротивлении участка. Например, для схемы (рис. 1, а) φС = φА – I2R2 . Если на горизонтальной оси откладывать последовательно сопротивление участков, обходя контур по часовой стрелке, а на вертикальной – потенциал точек, то для первой, второй и третьей схем соединения (рис. 1. а, б, в) получаем кусочно-линейные зависимости (рис. 2 а, б, в). Тангенсы углов наклона графика, с учетом масштабных коэффициентов осей сопротивлений (mR ) и потенциалов (mU), пропорциональны токам ветвей.
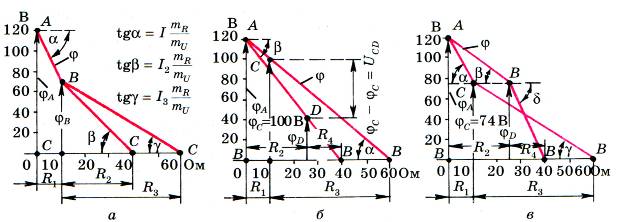
Рис. 2.
Для произвольного контура (рис. 3), зная токи, сопротивления, ЭДС ветвей, на основании закона Ома для активного участка цепи вычисляют потенциалы промежуточных точек. Затем строят потенциальную диаграмму. Согласно закона Ома, U12 = φ1 – φ2 – I1R1. Зададим условно нулевое значение потенциала φ1 точки 1 (узел 1 заземлен). Тогда φ2 = - I1R1 φ3, или U43 = φ4 – φ3 = I2R2 > 0. Благодаря этому φ4 = φ3 + I2R2 = (Е1 - I1R1) + I2R2. Напряжение U54 = φ5 – φ4 = - Е2, откуда φ5 = φ4 - Е2. Ветвь 5 – 6 – 7 – 8 разорвана, ток I3 в ней отсутствует и U75 = U76 = U85 = φ8 – φ5, где φ5 уже определено, а U76 известно. Тогда φ8 = U76 + φ5. Для ветви 8 – 9 – 1: φ9 – φ8 = - Е3, или φ9 = φ8 - Е3 и φ1 – φ9 = + I4R4, что в соответствии с начальным условием должно быть равно нулю (условие проверки).
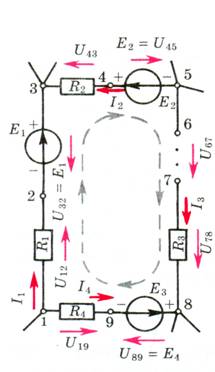
Рис. 3.
График распределения потенциала по контуру (рис. 4) дает представление о разности потенциалов между любыми двумя точками контура. Например, U49 = φ4 – φ9 максимальна, что учитывается при конструктивном внедрении схемы в конкретной установке. Необходимо обеспечить надежную электрическую изоляцию этих точек или разнести их в пространстве, чтобы не было электрического пробоя диэлектрика. Чем большее расстояние l между этими точками, тем меньшая напряженность электрического поля ε = U49/l.
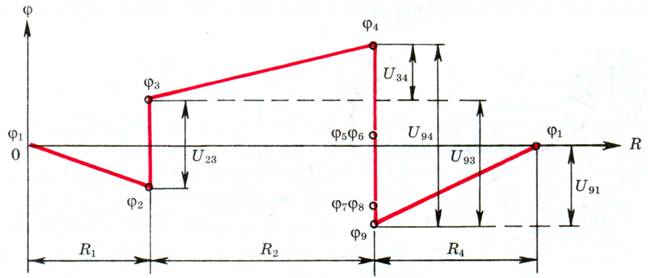
Рис. 4.
На рис. 2.2 выбираем замкнутый контур, включавший обе эдс. Для построения потенциальной диаграммы пронумеруем рассматриваемый контур цепи и примем потенциал какой-либо точки равным нулю (например, точки I, т.е. φ1 = 0 (см. рис. 2.2). Точки контура 1, 2, 3, 4, 5, I ставим после каждого элемента схемы.
Потенциалы других точек относительно точки I (φ1 = 0) определяются следующим образом:
На потенциальной диаграмме откладываются потенциалы отдельных точек выбранного контура по отношению к одной точке, потенциал которой принят за нуль. Порядок расположения выбранных точек должен соответствовать порядку расположения каждого элемента на схеме с учетом величины его сопротивления. При таком построении каждой точке контура соответствует определенная точка на потенциальной диаграмме.
Приняв масштабы для единиц потенциала (mφ) и сопротивления (mR), построим потенциальную диаграмму.

Рис. 2.5. Потенциальная диаграмма контура
Для данного примера приняты следующие масштабы: mφ = 2 B/мм; mR = 0,25 Ом/мм.
По построенной потенциальной диаграмме (рис. 2.5) можно определить напряжение между любыми точками выбранного контура, что бывает необходимо при анализе работы схемы.
ЗАДАНИЕ № 2. РАСЧЕТ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
Задание на расчет цепи
По выданному преподавателем номеру варианта (№B) и значению К необходимо по табл. 1.1 данных указаний определить номер расчетной схемы (№cx) и вариант параметров схемы (№п), которые затем находят на рис. 3.1 и табл. 3.1 соответственно.





Рис. 3.1 Расчетные цепи (схемы) переменного тока
Значения параметров цепи (схемы) переменного тока
| Параметры цепи | R1 | R2 | R3 | X1 | X2 | X3 | X4 | X5 |
| Ncx, Nn | Ом | Ом | Ом | Ом | Ом | Ом | Ом | Ом |
e1 = 310 sin 314t B; e2 = 310 sin (314t + 60°) B; e3 = 141 sin (314t -30°) B
Примечание. Отсутствующие в схеме варианта задания параметры цепи (хотя они и указаны в табл. 3.1) необходимо принять равными нулю.
Для заданной цепи (схемы) необходимо выполнить следующее:
1.Рассчитать токи в ветвях методом контурных токов.
2.Определить активные и реактивные мощности источников эдс и всех пассивных элементов цепи.
3.Проверить правильность расчета токов, составив уравнения баланса активных и реактивных мощностей цепи.
4.Построить векторную диаграмму токов на комплексной плоскости.
5.Записать уравнения для мгновенных значений токов.
6.Исключить один из источников в схеме, соединив накоротко точки, к которым он присоединялся.
7.В полученной простой цепи со смешанным соединением элементов рассчитать токи во всех ветвях символическим методом.
8.Определить активную, реактивную и полную мощности цепи, а также активные и реактивные мощности всех ее элементов.
9.Выполнить проверку расчета, составив уравнения баланса активной и реактивной мощностей цепи..
10. Рассчитать коэффициент мощности цепи (cosφ) и определить его характер (отстающий или опережающий).
Литература: [1, с. 79. 126; 2, с. 72. 107].
3.2. Примерный перечень вопросов для защиты задания
1. Дать определения синусоидальной величины и основных её параметров: амплитуды, начальной фазы, частоты, угловой частоты.
2. Почему действующее значение синусоидальной величины является её основной характеристикой?
3. Показать связь между синусоидальной величиной и изображающим её вектором и комплексом.
4. С какой целью синусоидальные величины изображают векторами и комплексными числами?

5. Что такое векторная диаграмма?
6. Можно ли на векторной диаграмме изображать синусоидальные величины, изменяющиеся с разной частотой?
7. Объясните, почему при постоянном напряжения включение в цепь конденсатора равносильно разрыву цепи, а при переменном напряжении ток через емкость проходит?
8. Почему индуктивности элементов цепи учитывают при расчете переменных токов и не учитывают при расчете постоянных?
9. Как учитывают емкости и индуктивности элементов при расчете цепей синусоидального тока?
10. Как определить сдвиг фаз напряжения и тока цепи (угол φ)?
11. Что характеризует коэффициент мощности (cos φ)? Почему на практике стремятся увеличить cos φ ?
12. Что понимают под активной, реактивной и полной мощностями цепи? Как они рассчитываются?
13. В каких цепях возникает резонанс напряжения (тока) и почему он так называется? Каково значение коэффициента мощности при резонансе и почему оно такое?
14. В чем сущность символического метода расчета цепей переменного тока?
Пример расчета цепи синусоидального тока
Для схемы рис. 3.2 заданы: величины эдс и параметры цепи
e1 = 310 ∙ sin(314 t + 30°) B; е2 = З14 sin (314 t - 60°) B;
RI = 10 Ом; R2 = 15 Ом; R3 = 5 Ом;
xI = 32 Ом; x2 = 8 Ом; x3 = 22 Ом; x4 = 10 Ом.
Читайте также:


