Как сделать параллельный перенос
Конспект
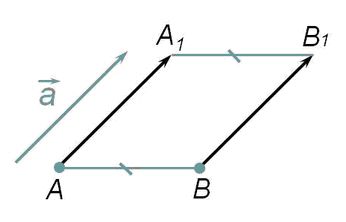
Отметим точки A, B и зададим некоторый вектор а. Отложим вектор а от каждой из точек. При этом точка А отображается в точку А1, точка В отображается в точку В1. Таким образом вектор АА1 равен вектору ВВ1 и равны вектору а. Этот вид отображения плоскости на себя называется параллельным переносом.
Проведем отрезок АВ. Отложим вектор р от точек А и В. При этом точка А отображается в точку А1, точка В отображается в точку В1. Проведем отрезок А1В1. Отрезок АВ отображается на отрезок А1В1 при параллельном переносе на вектор р.
Построим треугольник ABC и задаем некоторый вектор а. Отложим вектор р от каждой из точек А, В, С. При этом точка А отображается в точку А1, точка В отображается в точку В1, точка С отображается в точку С1. Таким образом векторы АА1 = ВВ1 = СС1 и равны вектору а. Соединим отрезками точки А1, В1, С1. Треугольник АВС отображается на треугольник А1В1С1 при параллельном переносе на вектор а.
Сформулируем определение. Параллельным переносом на вектор р называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М1, что вектор ММ1 = р. Является ли параллельный перенос движением – отображением плоскости на себя, сохраняющим расстояние?
Пусть при параллельном переносе на вектор а точки M и N отображаются в точки M1 и N1. Так как вектор MM1 равен вектору a и вектор NN1 равен вектору a, то векторы MM1 и NN1 равны, т.е. MM1 = NN1, MM1 ║ NN1 следовательно, четырехугольник – параллелограмм, т.е. MN = M1N1. Значит, расстояние не изменяется. Таким образом доказали, что параллельный перенос является движением. Отметим следующие свойства.
При параллельном переносе:
1) отрезок переходит в равный ему отрезок;
2) угол переходит в равный ему угол;
3) окружность переходит в равную ей окружность;
4) любой многоугольник переходит в равный ему многоугольник;
5) параллельные прямые переходят в параллельные прямые;
6) перпендикулярные прямые переходят в перпендикулярные прямые.
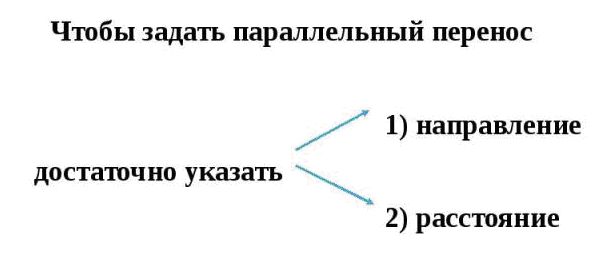
Чтобы задать параллельный перенос достаточно задать некоторый вектор т.е. указать направление и расстояние.
Пусть на плоскости задана геометрическая фигура. Если каждую точку данной фигуры переместить на некоторое расстояние, так чтобы расстояние между точками сохранилось, то мы получим новую фигуру, преобразованную из данной. (Рис.1) Таким образом, преобразование одной фигуры в другую так, что расстояние между точками остается неизменным, называется движением.
Например, при перемещении фигуры М на некоторое расстояние получим фигуру М1. Все точки фигуры М передут в точки фигуры М1. Расстояние между точками сохранится АВ = А1В1
Свойства движения
При движение все точки, лежащие на прямой, перейдут в точки также лежащие на прямой. Порядок их взаимного расположения останется неизменным. Т.е. Прямые переходят в прямые, полупрямые - в полупрямые, отрезки - в отрезки и т.д. При движении градусная мера угла между двумя полупрямыми останется неизменной.

Рис.1 Движение и его свойства.
2.Симметрия относительно точки
Пусть на плоскости задана точка О. (Рис.2) Возьмем произвольную точку А. Если через точки О и А провести прямую и отложить от точки О отрезок ОА', равный отрезку АО, то точка О будет называться точкой симметрии. А точка А' - точкой симметричной точке А относительно точки О.
При преобразовании фигур каждая точка переходит в симметричную ей точку относительно точки симметрии О. Такое преобразование называется преобразованием симметрии, а фигуры называются симметричными относительно точки О.
Если при преобразовании фигура переходит в саму себя, то она называется центрально-симметричной, а точка О называется точкой симметрии. Например, параллелограмм, окружность, эллипс, ромб, квадрат.
Преобразование фигур относительно точки симметрии является движением.

Рис.2 Симметрия относительно точки.
3.Симметрия относительно прямой
Пусть дана прямая а. (Рис.3). Если взять произвольную точку, например точку Е, провести перпендикуляр к прямой а и на продолжении этого перпендикуляра отложить отрезок ВE', равный отрезку ЕВ, то точка Е' будет симметрична относительно прямой а. Если точка лежит на прямой а, то она симметрична сама себе.
При преобразовании фигуры в фигуру каждая точка переходит в точку С', симметричную относительно прямой а. Такое преобразование называется преобразование симметрии относительно прямой.
Преобразование симметрии относительно прямой также является движением, т.к. согласно определению движения расстояние между точками фигуры при смещении относительно прямой не изменяется.

Рис.3 Симметрия относительно прямой.
4.Параллельный перенос и его свойства
Пусть на плоскости с осями координат Ox и Oy задана фигура S. Каждая точка фигуры параллельным переносом переходит в точку А' на одно и тоже расстояние. Тогда можно дать следующее определение: преобразование фигуры S в фигуру S', в котором каждая точка фигуры с координатами x и y смещается в точку с координатами x+a и y+b, где a и b постоянные числа, называется параллельным переносом.
Параллельный перенос есть движение, т.к. все точки смещаются на одно и тоже расстояние.
Таким образом, для получения координат новой фигуры, параллельный перенос задается следующими формулами:
x' = x + a
y' = y + b
Свойства параллельного переноса
При параллельном переносе все точки какой-либо фигуры смещаются по параллельным прямым на одно и тоже расстояние. Перпендикулярные прямые переходят в перпендикулярные прямые, параллельные прямые - в параллельные. Расстояния между точками какой-либо фигуры при перемещении, так же как и углы между прямыми, сохраняются.

Рис.4 Параллельный перенос и его свойства.
5.Пример 1
Докажите, что у параллелограмма точка пересечения диагоналей является центром симметрии.
Доказательство:
Пусть дан параллелограмм АВA'В' (Рис.5). По свойству параллелограмма, его диагонали делятся точкой пересечения пополам, а противолежащие стороны параллельны и равны. Следовательно, треугольники АОB' и ВОА' равны по двум сторонам и углу между ними. АО = ОА', ВО = ОB', углы при вершине О равны как вертикальные. А отсюда следует, что точки A' и B' симметричны точкам А и В относительно точки О. Т.е. получается, что вершины параллелограмма центрально симметричны относительно точки О.
Теперь на стороне АВ' возьмем произвольную точку Е и проведем через нее прямую, проходящую через точку О. Треугольники ЕОВ' и BOE' равны по второму признаку равенства треугольников: по стороне и прилегающим к ней углам. BO = OB' и углы при вершинах О и В,B' равны (при вершине О как вертикальные, при вершинах B,B' как внутренние накрест лежащие). Следовательно, отрезки ЕО и ОE' равны, т.е. ЕО = ОE'.

Рис.5 Задача. Докажите, что у параллелограмма.
Отсюда можно сделать вывод, что каждая точка Х параллелограмма переходит в точку X', симметричную относительно данной точки О. Т.е. преобразование симметрии относительно точки О переводит параллелограмм в сам себя, поэтому он называется центрально-симметричной фигурой, а точка О является его центром симметрии.
Пример 2
Докажите, что прямая, содержащая медиану равнобедренного треугольника, которая проведена к основанию, является его осью симметрии.
Доказательство:
Пусть АВА' данный равнобедренный треугольник с основанием АА', АВ = ВA' (Рис.6). Медиана ОВ лежит на прямой а. Так как медиана делит противолежащую сторону пополам, то треугольники АВО и A'BO равны по трем сторонам (АВ = ВA', АО = ОA', сторона ОВ у них общая). Следовательно, углы при вершине О равны 90°, как равные смежные углы. А углы при вершине В равны, так как треугольники равны. Следовательно, вершина треугольника А симметрична вершине A' относительно прямой а, так как основание АA' перпендикулярно прямой а. Так же как и для любой точки, принадлежащей отрезку АО, найдется симметричная ей точка на отрезке ОА' относительно прямой а.
Точка В лежит на прямой а, поэтому она симметрична сама себе относительно прямой а.
Теперь проведем произвольную прямую b, параллельную основанию АА'. Она пересечет боковые стороны треугольника в точках ЕЕ'. Рассмотрим треугольники ЕВО' и BO'E'. Они равны по второму признаку равенства треугольников (по стороне и прилегающим к ней углам: сторона BO' у них общая, углы при вершинах В и О' равны). Следовательно, ЕО' = O'E'.

Рис.6 Задача. Докажите, что прямая, содержащая медиану.
Отсюда следует, что любая точка Х' треугольника ВОА' симметрична точке Х треугольника АВО относительно прямой а, что является преобразованием симметрии относительно прямой. А если преобразование симметрии относительно прямой а переводит треугольник АВА' сам в себя, то прямая а является его осью симметрии.
Пример 3
Параллельный перенос задается формулами x' = x + 2, y' = y - 3. В какие точки при этом параллельном переносе переходят точки А (1;1), В (2;2), С (-2;0).
Решение:
По условию задачи параллельный перенос задается формулами:
x' = x + 2, y' = y - 3
Следовательно, точка А переходит в точку А' с координатами:
x' = 1 + 2 = 3, y' = 1 - 3 = -2, т.е. A' (3;-2).
Точка В переходит в точку В' с координатами:
x' = 2 + 2 = 4, y' = 2 - 3 = -1, т.е. В' (4;-1).
Точка С переходит в точку С' с координатами:
x' = -2 + 2 = 0, y' = 0 - 3 = -3, т.е. С' (0;-3). (Рис.7)

Рис.7 Задача. Параллельный перенос задается формулами.
Пример 4
Докажите, что если у двух ромбов равны диагонали, то они равны.
Доказательство:
Пусть даны два ромба: ABCD и A''B''С''D''. AC = A''C'', BD = B''D''. Углы между диагоналями равны 90°. Докажем, что они совмещаются движением, причем вершина А переходит в вершину A'', вершина В - в B'', вершина С - в С'', вершина D - в D''.
Подвергнем ромб ABCD преобразованию симметрии относительно прямой а, перпендикулярной отрезку СС' и проходящей через его середину (Рис.8). Если два ромба не располагаются друг под другом, то нужного расположения можно добиться при помощи параллельного переноса. (Напомним, что параллельный перенос также является движением со всеми вытекающими из этого свойствами.) В результате получим ромб A'B'C'D'. Если точки А и А' различны, то подвергнем его симметрии относительно прямой b, перпндикулярной отрезку A'A'' и проходящей через его середину и точку С'. Таким образом, отрезок A'C' перейдет в отрезок A''C''. И в результате получим ромб A''B'''C''D'''.
Преобразование симметрии относительно прямой является движением. А при движении точки переходят в точки, прямые - в прямые, углы между прямыми, так же как и расстояния между точками, сохраняются.

Рис.8 Задача. Докажите, что если у двух ромбов.
Отсюда следует, что отрезок B'''D''' перпендикулярен отрезку А''C'' и проходит через его середину, а точки B''' и D''' совпадают с точками B'' и D'', так как по условию задачи диагонали двух ромбов равны. Таким образом, получается, что диагонали ромба АС и BD полностью совпадут с диагоналями A''C'' и B''D''. А из этого следует, что и вершины ромба ABCD полностью совпадут с вершинами ромба A''B''C''D'', так как они находятся на концах диагоналей. Следовательно, ромб ABCD полностью перейдет в ромб A''B''C''D''.
Пример 5
Существует ли параллельный перенос, при котором точка А (2;2) переходит в точку A'(3;-2), а точка В (-2;1) переходит в точку В'(-2;-3).
Решение:
Параллельный перенос задается формулами:
x' = x + a, y' = y + b
где а и b одни и те же числа. Отсюда следует, что
a = x' - x, b = y' - y. Подставим координаты точки А и A':
a = 3 - 2, b = -2 - 2; т.е. a = 1, b = -4
Следовательно, параллельный перенос по точке А задается формулами: x' = x + 1, y' = y - 4
Параллельный перенос и его свойства
Содержание
Общие сведения о параллельном переносе
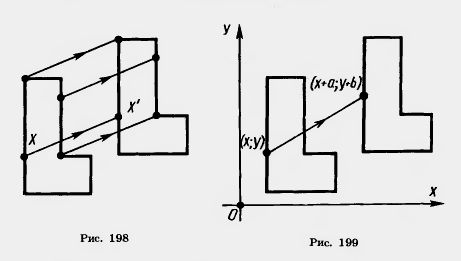
Введем на плоскости декартовы координаты х, у. Преобразование фигуры F, при котором произвольная ее точка (х; у) переходит в точку (х + а; у + b), где а и b одни и те же для всех точек (х; у), называется параллельным переносом (рис. 199). Параллельный перенос задается формулами x' = x + а, у' = у + b.
Эти формулы выражают координаты х', у' точки, в которую переходит точка (х; у) при параллельном переносе.
Свойства параллельного переноса
Параллельный перенос есть движение.
Действительно, две произвольные точки А(х1; у1) к В (х2; у2) переходят при параллельном переносе в точки А' (х1 +а; у1 + b), В'(х2 + а; y2+b). Поэтому
АВ 2 =(х2-х1) 2 + (у2-у1 ) 2
Отсюда АВ=А'В'. Таким образом, параллельный перенос сохраняет расстояния, а значит, является движением, что и требовалось доказать.
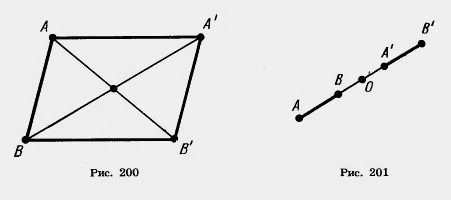
Действительно, пусть точки A (x1; y1) и В (x2; y2) переходят в точки A'(x1+а; y1 + b) и В' (х2 + а; y2 + b) (рис. 200). Середина отрезка АВ' имеет координаты
![]()
Те же координаты имеет и середина отрезка А'В. Отсюда следует, что диагонали четырехугольника АА'В'В пересекаются и точкой пересечения делятся пополам. Значит, этот четырехугольник — параллелограмм. А у параллелограмма противолежащие стороны А А' и ВВ' параллельны и равны.
Заметим, что у параллелограмма АА'В'В параллельны и две другие противолежащие стороны — АВ и А 'В'. Отсюда следует, что при параллельном, переносе прямая переходит в параллельную прямую (или в себя).
Замечание. В предыдущем доказательстве предполагалось, что точка В не лежит на прямой АА'. В случае, когда точка В лежит на прямой АА', точка В' тоже лежит на этой прямой, так как середина отрезка АВ' совпадает с серединой отрезка ВА' (рис. 201). Значит, все точки А, В, А', В' лежат на одной прямой. Далее,
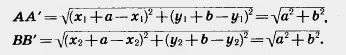
Таким образом, в этом случае точки АиВ смещаются по прямой АВ на одно и то же расстояние а прямая АВ переходит в себя.
Повторение темы о параллельном переносе
Мы с вами уже познакомились с такой темой, как параллельный перенос. На этом уроке вы узнали, что такое преобразование на плоскости, где все точки перемещаются на одно и то же расстояние, считается параллельным переносом.
Из данного урока, каждому из вас стало понятно, что параллельный перенос является движением, так как при таком переносе любая прямая переходит в такую же параллельную ей прямую.
Если мы посмотрим на рисунок, то можем наглядно представить такое движение, как сдвиг площади в направлении данного вектора на его длину.
Свойства, которыми обладает параллельный перенос в пространстве
• Во-первых, параллельный перенос является движением;
• Во-вторых, при выполнении этого действия все точки смещаются по параллельным прямым и притом на одно и то же расстояние;
• В-третьих, при таком переносе прямая имеет свойство переходить в такую же параллельную прямую или в себя саму;
• В-четвертых, независимо от того, какими точками были A и A', но точка A переходит в точку A'.
• В-пятых, при таком переносе, т.е параллельном переносе в пространстве, в любом случае плоскость имеет свойство переходить в себя саму или же такую же параллельную ей плоскость.
Истрия и применение в науке
Как правило, в каждого понятия есть свой первооткрыватель, но автор параллельного переноса в пространстве, на жаль, нам неизвестен. А вот применение параллельного переноса в пространстве довольно широко. Как правило, такой перенос используют при преобразовании графической функции в математике, в механике, а также в кристаллографии.

Но если рассматривать трансляция или кристаллографию, то в этом случае перенос приобретает симметричное преобразование, в котором узел пространственной решётки должен совпасть с идентичным ближайшим узлом. В принципе, трансляцию можно отнести к частному случаю параллельного переноса, так как при сдвиге на определенный вектор ее свойства в данной системе не изменяются, а являются вектором трансляции и для нее свойственна трансляционная симметрия.
Примеры из жизни
В повседневной жизни мы с вами также постоянно сталкиваемся с примерами параллельного переноса в пространстве. Таким наглядным примером может быть, применяемая в строительной индустрии скользящая опалубка, этот процесс мы можем наблюдать и при перестановке мебели в квартире, да и следы от подошвы нам также напоминают о параллельном переносе в пространстве.
А также, параллельный перенос можно встретить и в таких необычных ситуациях:

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Сертификат и скидка на обучение каждому участнику

Параллельный перенос, симметрия относительно плоскости.
Сформировать понятие параллельного переноса;
Рассмотреть симметрию относительно плоскости.
Параллельный перенос
Параллельным переносом фигуры называется перенос всех точек пространства на одно расстояние в одном направлении.
Параллельный перенос определяет вектор, по которому совершается перенос.
Чтобы совершить параллельный перенос, нужно знать направление и расстояние, что означает задать вектор.
Чтобы при параллельном переносе построить изображение многоугольника, достаточно построить изображения вершин этого многоугольника.
Первоначальная фигура и фигура, полученная после параллельного переноса, равны.
Параллельный перенос используется для конструирования графиков функций.
На рисунке изображена парабола и два результата параллельного переноса.
Иногда параллельный перенос встречается в необычных ситуациях:

Симметрия
Математически строгое представление о симметрии сформировалось сравнительно недавно – в XIX веке. В наиболее простой трактовке известного немецкого математика Германа Вейля (1855-1955) современное определение симметрии выглядит так: симметричным называется такой объект, который можно как-то изменять, получая в результате то же, с чего начали.
Мы будем называть симметрией фигуры любое преобразование, переводящее фигуру в себя, т.е. обеспечивающее ее самосовмещение.
Перечислим виды симметрии.
Виды симметрии
Осевая симметрия
Преобразование, при котором каждая точка A фигуры (или тела) преобразуется в симметричную ей относительно некоторой оси l точу А, при этом отрезок AA´ l , называется осевой симметрией.
Если точка А лежит на оси l, то она симметрична самой себе, т.е. A совпадает с A´.
В частности, если при преобразовании симметрии относительно оси l,
фигура F переходит сама в себя, то она называется симметричной относительно оси l, а ось l называется ее осью симметрии.
Центральная симметрия.
Преобразования, переводящее каждую точку A фигуры или тела в точку A´, симметричную ей относительно центра O, называется преобразованием центральной симметрии или просто центральной симметрией.

Точка O называется центром симметрии и является неподвижной. Других неподвижных точек это преобразование не имеет. Если при преобразовании центральной симметрии относительно центра О фигура F преобразуется в себя, то она называется симметричной относительно центра O.при этом центр O называется центром симметрии фигуры F. Примерами фигур, обладающих центром симметрии, являются параллелограмм, окружность и т.д.
Знакомые понятия поворота и параллельного переноса используются при определении так называемой трансляционной симметрии.
Рассмотрим трансляционную симметрию более подробно.
Трансляционная симметрия
Поворот
Преобразование, при котором каждая точка A фигуры или тела поворачивается на один и тот же угол α вокруг заданного центра O, называется вращением или поворотом плоскости . Точка О называется центром вращения, а угол α – углом вращения. Точка O является неподвижной точкой этого преобразования.

Центральная симметрия есть поворот фигуры или тела на 180˚.
Параллельный перенос.
Преобразование при котором каждая точка фигуры или тела перемещается в одном и том же направлении на одно и то же расстояние, называется параллельным переносом .
Чтобы задать преобразование параллельного переноса, достаточно задать вектор .
Скользящая симметрия
Скользящей симметрией называется такое преобразование, при котором последовательно выполняются осевая симметрия и параллельный перенос.

Все перечисленные преобразования будем называть преобразованиями симметрии. Для преобразований симметрии имеют место следующие свойства:
отрезок переходит в равный ему отрезок;
угол переходит в равный ему угол;
окружность переходит в равную ей окружность;
любой многоугольник переходит в равный ему многоугольник и т.д.
параллельные прямые переходят в параллельные, перпендикулярные в перпендикулярные.
Читайте также:


