Как сделать описанную окружность
\u0426\u0435\u043d\u0442\u0440 \u043e\u043f\u0438\u0441\u0430\u043d\u043d\u043e\u0439 \u043e\u043a\u0440\u0443\u0436\u043d\u043e\u0441\u0442\u0438 - \u043f\u0435\u0440\u0435\u0441\u0435\u0447\u0435\u043d\u0438\u0435 \u0441\u0435\u0440\u0435\u0434\u0438\u043d\u043d\u044b\u0445 \u043f\u0435\u0440\u043f\u0435\u043d\u0434\u0438\u043a\u0443\u043b\u044f\u0440\u043e\u0432 \u0441\u0442\u043e\u0440\u043e\u043d.
\u041d\u0443\u0436\u043d\u043e \u043f\u043e\u0441\u0442\u0440\u043e\u0438\u0442\u044c \u0441\u0435\u0440\u0435\u0434\u0438\u043d\u043d\u044b\u0435 \u043f\u0435\u0440\u043f\u0435\u043d\u0434\u0438\u043a\u0443\u043b\u044f\u0440\u044b \u043a \u0434\u0432\u0443\u043c \u0441\u0442\u043e\u0440\u043e\u043d\u0430\u043c.
\u0414\u043b\u044f \u0442\u043e\u0433\u043e, \u0447\u0442\u043e\u0431\u044b \u043f\u043e\u0441\u0442\u0440\u043e\u0438\u0442\u044c \u0441\u0435\u0440\u0435\u0434\u0438\u043d\u043d\u044b\u0439 \u043f\u0435\u0440\u043f\u0435\u043d\u0434\u0438\u043a\u0443\u043b\u044f\u0440 \u043a \u043e\u0442\u0440\u0435\u0437\u043a\u0443, \u043d\u0443\u0436\u043d\u043e \u043f\u0440\u043e\u0432\u0435\u0441\u0442\u0438 \u0434\u0432\u0435 \u043e\u043a\u0440\u0443\u0436\u043d\u043e\u0441\u0442\u0438 \u0441 \u0446\u0435\u043d\u0442\u0440\u0430\u043c\u0438 \u0432 \u043a\u043e\u043d\u0446\u0430\u0445 \u043e\u0442\u0440\u0435\u0437\u043a\u0430 \u0438 \u0447\u0435\u0440\u0435\u0437 \u0442\u043e\u0447\u043a\u0438 \u043f\u0435\u0440\u0435\u0441\u0435\u0447\u0435\u043d\u0438\u044f \u043e\u043a\u0440\u0443\u0436\u043d\u043e\u0441\u0442\u0435\u0439\u00a0 \u043f\u0440\u043e\u0432\u0435\u0441\u0442\u0438 \u043f\u0440\u044f\u043c\u0443\u044e.">]" data-testid="answer_box_list">

Центр описанной окружности - пересечение серединных перпендикуляров сторон.
Нужно построить серединные перпендикуляры к двум сторонам.
Для того, чтобы построить серединный перпендикуляр к отрезку, нужно провести две окружности с центрами в концах отрезка и через точки пересечения окружностей провести прямую.
Новые вопросы в Математика
5) Найдите значения тригонометрических отношений для углов, конечная сторона которых проходит через точки. a) (-1, 1) b) (-1, 0) c) (1, -1)
ПОМГИТЕ ПЖ Какое наибольшее количество ферзей можно поставить на доску 6×8 с вырезанным в центре квадратом 2×2 так, чтобы они не били друг друга? Подр … азумевается, что ферзь бьёт все клетки, расположенные по вертикалям, горизонталям и обеим диагоналям. Ферзь не бьет сквозь вырезанные клетки.
помогите пожалуйста сумма длинн всех рёбер прямоугольного паралепипеда равна 96 см, два его измерения равны 7 см и 12 см. найдите третье измерение пар … алепипеда.
Есть 10 сумок, в каждой из которых 100 идентичных монет. Во всех сумках (кроме одной) монеты весят по 10 грамм. Однако в контрафактной сумке все монет … ы весят либо 9, либо 11 грамм. Сможете ли Вы определить контрафактную сумку за одно взвешивание с помощью точных весов? Помогите пожалуйста до воскресенья надо сделать
Кругова діаграма показує уподобання хлопців 6-Ы щодо кінофільмів; пригоди, фантастика і бойовики (мал. 52). Відомо, що: 1) більшість хлопців надають п … еревагу приго- дам; 2) Фантастику полюбляють найменше. Скільки хлопців

Описанная окру́жность многоугольника — окружность, содержащая все вершины многоугольника. Центром является точка (принято обозначать ) пересечения серединных перпендикуляров к сторонам многоугольника.
Содержание
Свойства
- Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам. Как следствие: если рядом с n-угольником описана окружность, то все серединные перпендикуляры к его сторонам пересекаются в одной точке (центре окружности).
- Около любого правильногомногоугольника можно описать окружность, и притом только одну.
Для треугольника

- Около треугольника можно описать окружность, притом только одну. Её центром будет являться точка пересечения серединных перпендикуляров.
- У остроугольного треугольника центр описанной окружности лежит внутри, у тупоугольного — вне треугольника, у прямоугольного — на середине гипотенузы.
Обозначаем буквой О точку пересечения серединных перпендикуляров к его сторонам и проведем отрезки ОА, ОВ и ОС. Так как точка О равноудалена от вершин треугольника АВС, то ОА = OB = ОС. Поэтому окружность с центром О радиуса ОА проходит через все три вершины треугольника и, значит, является описанной около треугольника ABC.
- 3 из 4 окружностей, описанных относительно серединных треугольников (образованных средними линиями треугольника), пересекаются в одной точке внутри треугольника. Эта точка и есть центр описанной окружности основного треугольника.
- Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника.
- Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
Радиус
Радиус описанной окружности может быть найден по формулам
" width="" height="" />
" width="" height="" />
> = \frac>" width="" height="" />
Где:
— стороны треугольника,
— угол, лежащий против стороны ,
— площадь треугольника. — полупериметр треугольника.
Положение центра описанной окружности
Пусть _A, <\mathbf r>_B, <\mathbf r>_C" width="" height="" />
радиус-векторы вершин треугольника, _O " width="" height="" />
— радиус-вектор центра описанной окружности. Тогда

При этом - длины сторон треугольника, противоположных вершинам .
Уравнение описанной окружности
Пусть _A = (x_A, y_A), <\mathbf r>_B = (x_B, y_B), <\mathbf r>_C= (x_C, y_C)" width="" height="" />
координаты вершин треугольника в некоторой декартовой системе координат на плоскости, _O= (x_O, y_O) " width="" height="" />
— координаты центра описанной окружности. Тогда


Для точек , лежащих внутри окружности, определитель отрицателен, а для точек вне ее — положителен.
Для четырехугольника

Вписанный простой (без самопересечений) четырёхугольник необходимо является выпуклым.
Около выпуклого четырёхугольника можно описать окружность тогда и только тогда, когда сумма его внутренних противоположных углов равна 180° (π радиан).
Можно описать окружность около:
- любого прямоугольника (частный случай квадрат)
- любой равнобедренной трапеции
У четырёхугольника, вписанного в окружность, произведение длин диагоналей равно сумме произведений длин пар противоположных сторон: [1]
Для многоугольника
- Если из отрезков составить многоугольник, то его площадь будет максимальна, когда он вписанный.
- Если точка равноудалена от вершин многоугольника, то она проектируется в центр окружности, описанной около этого многоугольника.
В сферическом треугольнике
Описанная окружность для сферического треугольника — это окружность, содержащая все его вершины.
- Если A, B, C — углы сферического треугольника, P — их полусумма, то тангенс радиуса [2] описанной окружности будет равен [3] :78,83
- Описанная окружность принадлежит сфере. Радиус, проведенный из центра сферы через центр описанной окружности пересечет сферу в точке пересечения серединных перпендикуляров (больших кругов сферы, перпендикулярных сторонам в их середине) к сторонам сферического треугольника [3] :21-22 .
См. также
Примечания
- ↑Теорема Птолемея
- ↑ Здесь радиус окружности измеряется по сфере, то есть представляет собой градусную меру дуги большого круга, соединяющей точку пересечения радиуса сферы, проведенного из центра сферы через центр окружности, со сферой и вершину треугольника.
- ↑ 12Степанов Н. Н. Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — 154 с.
Литература
- Элементарная геометрия / Киселёв А.П.. — М .: Просвещение, 1980.
- Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М .: Просвещение, 1991. — С. 87. — 383 с. — ISBN 5-09-001287-3
- Понарин Я. П. Элементарная геометрия. В 2 тт. — М .: МЦНМО, 2004. — С. 53-54. — ISBN 5-94057-170-0
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое "Описанная окружность" в других словарях:
Окружность — и её центр Окружность геометрическое место всех точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное неотрицательное расстояние, называемое её радиусом. Содержание … Википедия
Окружность девяти точек — 9 точек Окружность девяти точек это окружность, проходящая через середины всех трёх сторон треугольника. Она также назы … Википедия
Окружность Эйлера — В геометрии треугольника окружность девяти точек это окружность, проходящая через середины всех трёх сторон треугольника. Она также называется окружностью Эйлера, окружностью Фейербаха, окружностью шести точек. Окружность девяти точек получила… … Википедия
Вписанная окружность — Окружность, вписанная в многоугольник ABCDE Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон. Центр окружности, вписанной в угол, лежит на биссектри … Википедия
Вневписанная окружность — Вписанная (с центром I) и 3 вневписанные (с центрами в J) окружности в Вневписанная … Википедия
основная окружность конического зубчатого колеса с циклоидальной линией зубьев — Концентрическая окружность на развертке делительного конуса конического зубчатого колеса, при качении по которой другой окружности, называемой паллоидной, точка, жестко связанная с паллоидной окружностью, образует линию зуба в форме удлиненной… … Справочник технического переводчика
прилегающая окружность — Окружность минимального диаметра, описанная вокруг реального профиля наружной поверхности вращения, или окружность максимального диаметра, вписанная в реальный профиль внутренней поверхности вращения. Примечание В тех случаях, когда расположение… … Справочник технического переводчика
Основная окружность конического зубчатого колеса с циклоидальной линией зубьев — 163. Основная окружность конического зубчатого колеса с циклоидальной линией зубьев Концентрическая окружность на развертке делительного конуса конического зубчатого колеса, при качении по которой другой окружности, называемой паллоидной, точка,… … Словарь-справочник терминов нормативно-технической документации
начальная окружность ротора — Описанная вокруг оси технологического или транспортного ротора окружность, на которой расположены условные центры позиций ротора. [ГОСТ 14334 87] Тематики роторные и роторно конвейерные линии … Справочник технического переводчика
Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.
Радиусом называется любой отрезок соединяющей точку окружности с ее центром.
Чтобы построить окружность необходимо знать уравнение окружности:
(х – а) 2 + (у – b) 2 = R 2
Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.
И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:
Пример №1:
(х – 1) 2 + (у – 2) 2 = 4 2
Найдем центр окружности:
х – 1=0
x=1
Центр окружности будет находится в точке (1;2)
Найдем радиус окружности:
R 2 =4
R 2 =2 2
R=2
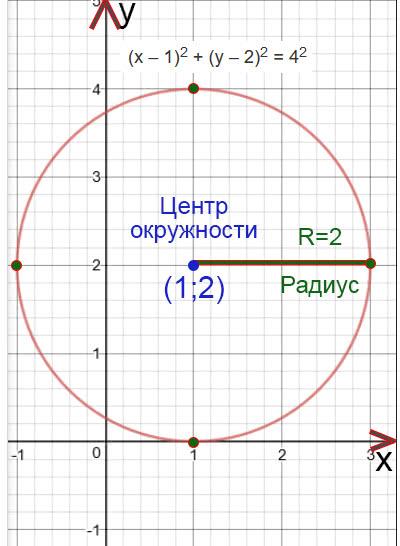
Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность.
Пример №2:
х 2 + (у + 1) 2 =1
Можно представить уравнение окружности ввиде:
(х-0) 2 + (у + 1) 2 =1 2
Найдем центр окружности:
х=0
Центр окружности будет находится в точке (0;–1)
Найдем радиус окружности:
R 2 =1
R 2 =1 2
R=1

Построим окружность.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Описанные и вписанные окружности
Наглядная геометрия 9 класс. Опорный конспект 2 Описанные и вписанные окружности
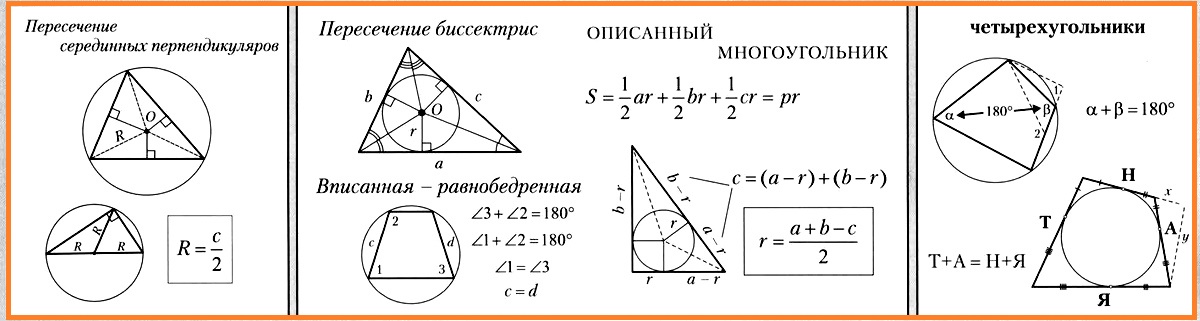
Около любого треугольника можно описать окружность. Она проходит через все вершины треугольника. Вы уже знаете, что точка пересечения серединных перпендикуляров равноудалена от вершин треугольника. Она и является центром описанной окружности.
В любой треугольник можно вписать окружность. Она касается всех сторон треугольника. Вы также знаете, что точка пересечения биссектрис треугольника равноудалена от сторон треугольника. Она и является центром вписанной окружности.
А можно ли описать окружность около любого параллелограмма? Если попробовать это сделать, то окажется, что около параллелограмма можно описать окружность, только если он — прямоугольник. Мы узнаем, каким свойством обладают вписанные и описанные четырехугольники и какие признаки позволяют судить о том, можно ли около данного четырехугольника описать и можно ли в него вписать окружность.
И вдобавок мы познакомимся с одной важной формулой площади треугольника S = рr.

1. Окружность, описанная около треугольника.
Окружность называется описанной около треугольника, если она проходит через все его вершины.
Теорема. Вокруг любого треугольника можно описать окружность, и только одну. Ее центр лежит на пересечении серединных перпендикуляров к сторонам треугольника.
Доказательство. Точка пересечения серединных перпендикуляров к сторонам треугольника равноудалена от его вершин (доказано нами в 7 классе). Поэтому она является центром описанной окружности, расстояние от этой точки до любой из вершин равно радиусу.
Если существует еще одна описанная окружность, то ее центр равноудален от всех трех вершин и поэтому совпадает с точкой пересечения серединных перпендикуляров, а радиус совпадает с радиусом первой окружности. Окружности совпадают.
2. Окружность, описанная около прямоугольного треугольника.
Теорема. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а радиус окружности равен половине гипотенузы.
Доказательство. Мы знаем, что медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы (доказано нами в 7 классе). Поэтому середина гипотенузы является центром описанной окружности, а ее радиус равен половине гипотенузы, т. е. R = c/2.
3. Окружность, вписанная в треугольник.
Окружность называется вписанной в треугольник, ест она касается всех сторон треугольника.
Теорема. В любой треугольник можно вписать окружность, и только одну. Ее центр лежит на пересечении биссектрис треугольника.
Доказательство. Точка пересечения биссектрис треугольника равноудалена от сторон треугольника (доказано нами в 7 классе). Если из этой точки опустить перпендикуляры на стороны и провести окружность радиусом, равным перпендикуляру, то стороны треугольника будут касаться окружности по признаку касательной.
Если существует еще одна вписанная окружность, то ее центр равноудален от всех трех сторон и поэтому совпадает с точкой пересечения биссектрис, а радиус совпадает с радиусом первой окружности. Окружности совпадают.
4. Формула площади S = рr.
Теорема. Площадь треугольника S = рr, где р — полупериметр треугольника, r — радиус вписанной окружности.
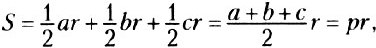
Доказательство. Соединим центр вписанной окружности с вершинами треугольника, стороны которого равны а, b и с. Получим три треугольника, для которых радиусы вписанной окружности, проведенные в точки касания, являются высотами. Площадь данного треугольника равна сумме площадей этих треугольников:
где p — полупериметр треугольника.
Данная формула справедлива для любого многоугольника, в который можно вписать окружность, т. е. для любого описанного многоугольника. Доказательство аналогично.
5. Окружность, вписанная в прямоугольный треугольник.
Теорема. Радиус окружности, вписанной в прямоугольный треугольник, находится по формуле r = (а + b – c)/2.
Доказательство. Проведем радиусы в точки касания. Получим квадрат со стороной r (четырехугольник, у которого все углы прямые и две соседние стороны равны по r) и отрезки катетов, равные r и а – r для катета а, r и b – r для катета b. Так как отрезки касательных, проведенных из одной точки, к окружности равны, то гипотенуза равна сумме отрезков (a – r) и (b – r). Так как с = (а – r) + (b – r), то r = (а + b – c)/2.
6. Свойство вписанного четырехугольника.
Теорема (свойство вписанного четырехугольника). Если четырехугольник вписан в окружность, то суммы его противоположных углов равны по 180°.
Доказательство. Противоположные углы α и β являются вписанными. Они опираются на дуги, которые дополняют друг друга до окружности. Окружность содержит 360°. Так как вписанный угол равен половине дуги, на которую он опирается, то сумма углов α и β равна 180°.
7. Признак вписанного четырехугольника.
Теорема (признак вписанного четырехугольника). Если сумма противоположных углов четырехугольника равна 180°, то вокруг него можно описать окружность.
Доказательство. Через три вершины четырехугольника всегда можно провести окружность (это вершины некоторого треугольника). Если четвертая вершина будет лежать внутри окружности или вне ее, то угол при этой вершине будет больше или меньше угла β, по свойству внешнего угла треугольника, т. е. 1 8. Свойство вписанной трапеции.
Теорема. Вписанная трапеция является равнобедренной.
Доказательство. 1-й способ. ∠1 + ∠2 = 180° как внутренние односторонние при параллельных прямых и секущей, ∠3 + ∠2 = 180° по свойству вписанного четырехугольника. Тогда ∠1 = ∠3 и трапеция равнобедренная по признаку равнобедренной трапеции.
2-й способ. Параллельные прямые отсекают равные дуги. Равные дуги стягиваются равными хордами. Поэтому боковые стороны трапеции равны.
9. Свойство описанного четырехугольника.
Теорема (свойство описанного четырехугольника). Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.
Доказательство. Отрезки касательных, проведенных из одной точки к окружности, равны. Обозначим равные отрезки соответственно одной черточкой, двумя, тремя и четырьмя. Убеждаемся, что суммы противоположных сторон равны: Т + А = Н + Я.
10. Признак описанного четырехугольника.
Теорема (признак описанного четырехугольника). Если у четырехугольника суммы противоположных сторон равны, то в него можно вписать окружность.
Доказательство. Пусть окружность касается только трех сторон. Повернув четвертую сторону вокруг вершины так, чтобы она касалась окружности, получим описанный четырехугольник.
Т + А = Н + Я — по свойству описанного четырехугольника,
Т + y = (Н + х) + Я — по условию.
Тогда y = А + х. А это противоречит неравенству треугольника у ЭТО НУЖНО ЗНАТЬ !

Читайте также:


