Как сделать односвязный список
Архитектура Связного списка (Linked List)
Для начала необходимо упомянуть, что существует несколько видов связных списков. Вот наиболее часто используемые из них:
- Односвязный список
- Двусвязный список
- Кольцевой список
Схематическая структура односвязного списка представлена на рисунке ниже.
Элемент данных добавляется в конец списка путем установки на него ссылки из элемента, который был крайним ранее. Таким образом, получается своеобразная цепочка, в которой каждый элемент данных имеет указатель на следующий.
В качестве примера рассмотрим тривиальную реализацию односвязного списка.
Элемент списка
Рассмотрим класс элемента связного списка. Для того, чтобы сделать его более универсальным мы используем Универсальный параметр T. Это позволит динамически указывать тип данных при использовании списка.
Список элементов
Теперь рассмотрим сам класс связного списка. Для него мы также используем Универсальный (generic) тип T, а также реализуем интерфейс IEnumerable, чтобы в дальнейшем было удобно перебирать элементы списка с помощью цикла foreach.
Использование
Ну и наконец нам остается проверить работу нашего списка. Для этого создадим несколько элементов и проверим работу списка.
Связный список (Linked List) представляет набор связанных узлов, каждый из которых хранит собственно данные и ссылку на следующий узел. В реальной жизни связный список можно представить в виде поезда, каждый вагон которого может содержать некоторый груз или пассажиров и при этом может быть связан с другим вагоном.
Таким образом, если в массиве положение элементов определяется индексами, то в связном списке - указателями на следующий и (или) на предыдущий элемент.
Связные списки могут различаться. Есть односвязные списки, в которых каждый узел хранит указатель только на следующий узел. Есть двусвязные списки: в них каждый элемент хранит ссылку как на следующий элемент, так и на предыдущий. Есть кольцевые замкнутые списки. В данном случае мы рассмотрим создание односвязного списка.
Перед созданием списка нам надо определить класс узла, который будет представлять одиночный объект в списке:
Класс Node является обобщенным, поэтому может хранить данные любого типа. Для хранения данных предназначено свойство Data . Для ссылки на следующий узел определено свойство Next .
Далее определим сам класс списка:
Разберем основные моменты. В зависимости от конкретных задач реализация списков может отличаться, но для всех реализаций характерны прежде всего два метода: добавление и удаление.
Но прежде чем выполнять различные операции с данными, в классе списка определяются три переменные:
Если у нас не установлена переменная head (то есть список пуст), то устанавливаем head и tail. После добавления первого элемента они будут указывать на один и тот же объект.
Если же в списке есть как минимум один элемент, то устанавливаем свойство tail.Next - теперь оно хранит ссылку на новый узел. И переустанавливаем tail - теперь она ссылается на новый узел.
Сложность данного метода составляет O(1) . Графически это выглядит так:
Важно отметить наличие переменной tail, которая указывает на последний элемент. Ряд реализаций не используют подобную переменную и добавляют иным образом:
Данный способ вполне рабочий и нередко встречается, однако необходимость перебора элементов для нахождения последнего увеличивает время на поиск и сложность алгоритма. Она равна O(n) .
Особняком стоит метод добавления в начало списка, где нам достаточно переустановить ссылку на головной элемент:
Алгоритм удаления элемента представляет следующую последовательность шагов:
Поиск элемента в списке путем перебора всех элементов
Установка свойства Next у предыдущего узла (по отношению к удаляемому) на следующий узел по отношению к удаляемому.
Для отслеживания предыдущего узла применяется переменная previous . Если элемент найден, и переменная previous равна null, то удаление идет сначала, и в этом случае происходит переустановка переменной head, то есть головного элемента.
Если же previous не равна null, то реализуются шаги выше описанного алгоритма.
Сложность такого алгоритма составляет O(n) . Графически удаление можно представить так:
Чтобы проверить наличие элемента, исползуется метод Contains:
Здесь опять же просто осуществляется перебор. Сложность алгоритма метода составляет O(n) .
И для того, чтобы список можно было бы перебрать во внешней прграмме с помощью цикла for-each, класс списка реализует интерфейс IEnumerable :
Реализация данного интерфейса не является неотъемлимой частью односвязных списков, однако предоставляет эффективный метод для перебора коллекции в цикле foreach. Иначе нам бы пришлось реализовать какие-то собственные конструкции по перебору списка.
Одномерный массив с возможностью его свободного изменения называется списком.
-- М. Сибуя, Т. Ямамото - Алгоритмы обработки данных
Связный список (linked list) это одна из простейших структур данных, состоящая из связных между собой объектов, называемых узлами (node). Каждый узел состоит из двух полей:
- данных; и
- указателя на следующий узел.
Графически узел будем представлять следующим образом:

Указатель next содержит или адрес следующего узла (рисунок A) или специальное значение NULL (нулевой указатель, рисунок B), которое используется как маркер конца списка.
Рассмотрим пример создания простейшего списка из трех элементов. Для начала создадим три узла и у каждого из них указатель next установим в значение NULL :
На рисунке показан результат создания трех независимых узлов:

Теперь свяжем узлы между собой:
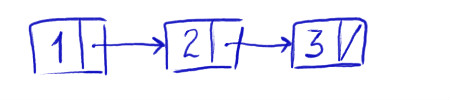
Таким образом, мы получили связный список, состоящий из трех элементов.
Связный список, содержащий только один указатель на следующий элемент, называется односвязным. Связный список, содержащий два поля указателя – на следующий элемент и на предыдущий, называется двусвязным.

Головой списка (head) называется его первый элемент, а последний элемент - хвостом (tail). Иногда для головы создают отдельный узел, не содержащий данных.
Реализация односвязного списка
Определим некоторые операции, которые можно выполнять над списками:
- добавление нового элемента в начало списка;
- добавление нового элемента в конец списка;
- удаление первого элемента в списке;
- удаление последнего элемента в списке;
- поиск элемента в списке;
- определение длины списка;
- объединение двух списков;
- и т.д.
Изменим структуру для отдельных элементов списка, сделав поле data указателем на void . Кроме того, для удобства работы добавим два пользовательских типа node_t и node_ptr_t .
В нашей реализации мы будем использовать пустой узел (т.е. узел без полезной нагрузки) в качестве головы списка:
Добавление элемента в начало списка:
Добавление элемента в конец списка:
Удаление элемента с головы списка:
Макрос для прохода по всем элементам списка:
Пример использования макроса для вывода всех элементов списка и вычисления его длины:
Задания
Задача 1: Напишите функцию list_reverse(L) , которая разворачивает список L .
Задача 2: Напишите функцию list_count(L, e) , которая подсчитывает число вхождений элемента e в список L .
Задача 3: Напишите функцию list_get(L, index) , которая возвращает элемент по индексу index .
Задача 4: Напишите функцию list_destroy(L) , которая освобождает память из под списка L (обратите внимание, что память нужно освобождать из под каждого элемента в отдельности).
Задача 5: Напишите функцию list_insert(L, index, e) , которая вставляет элемент e в список L по индексу index .
Задача 6: Напишите функцию list_merge(L1, L2) , которая объединяет список L1 cо списком L2 .
Связный список (англ. List) — структура данных, состоящая из элементов, содержащих помимо собственных данных ссылки на следующий и/или предыдущий элемент списка. С помощью списков можно реализовать такие структуры данных как стек и очередь.
Содержание
Простейшая реализация списка. В узлах хранятся данные и указатель на следующий элемент в списке.
![]()
Также хранится указатель на предыдущий элемент списка, благодаря чему становится проще удалять и переставлять элементы.

В некоторых случаях использование двусвязного списка в явном виде является нецелесообразным. В целях экономии памяти можно хранить только результат выполнения операции Xor над адресами предыдущего и следующего элементов списка. Таким образом, зная адрес предыдущего элемента, мы можем вычислить адрес следующего элемента.
Первый элемент является следующим для последнего элемента списка.

Рассмотрим базовые операции на примере односвязного списка.
Очевиден случай, когда необходимо добавить элемент ( [math]newHead[/math] ) в голову списка. Установим в этом элементе ссылку на старую голову, и обновим указатель на голову.

Для того, чтобы найти элемент по значению ( [math]value[/math] ), будем двигаться по списку от головы до конца и сравнивать значение в элементах с искомым. Если элемента в списке нет, то возвращаем [math]NULL[/math] .
Для того, чтобы удалить голову списка, переназначим указатель на голову на второй элемент списка, а голову удалим.

Удаление элемента после заданного ( [math]thisElement[/math] ) происходит следующим образом: изменим ссылку на следующий элемент на следующий за удаляемым, затем удалим нужный объект.

Для начала необходимо уметь определять — список циклический или нет. Воспользуемся алгоритмом Флойда "Черепаха и заяц". Пусть за одну итерацию первый указатель (черепаха) переходит к следующему элементу списка, а второй указатель (заяц) на два элемента вперед. Тогда, если эти два указателя встретятся, то цикл найден, если дошли до конца списка, то цикла нет.
Если цикла не существует, то заяц первым дойдет до конца и функция возвратит [math]false[/math] . В другом случае, в тот момент, когда и черепаха и заяц находятся в цикле, расстояние между ними будет сокращаться на [math]1[/math] , что гарантирует их встречу за конечное время.
Так как для поиска хвоста мы должны знать, что цикл существует, воспользуемся предыдущей функцией и при выходе из неё запомним "момент встречи" зайца и черепахи. Назовем её [math]pointMeeting[/math] .
Будем последовательно идти от начала цикла и проверять, лежит ли этот элемент на цикле. На каждой итерации запустим от [math]pointMeeting[/math] вперёд указатель. Если он окажется в текущем элементе, прежде чем посетит [math]pointMeeting[/math] снова, то точку окончания (начала) хвоста нашли.
Реализацию, приведенную выше можно улучшить. Для этого воспользуемся бинарным поиском. Сначала проверим голову списка, потом сделаем [math] 2 [/math] шага вперёд, потом [math] 4 [/math] , потом [math] 8 [/math] и так далее, пока не окажемся на цикле. Теперь у нас есть две позиции — на левой границе, где мы в хвосте, и на правой — в цикле. Сделаем бинарный поиск уже по этому отрезку и таким образом найдём цикл за [math]O(n \log n)[/math] .
Возможны два варианта цикла в списке. Первый вариант — сам список циклический (указатель [math]next[/math] последнего элемента равен первому), а второй вариант — цикл внутри списка (указатель [math]next[/math] последнего элемента равен любому другому (не первому)). В первом случае найти длину цикла тривиально, во второй случай сводится к первому, если найти указатель на начало цикла. Достаточно запустить один указатель из [math]pointMeeting[/math] , а другой из головы с одной скоростью. Элемент, где оба указателя встретятся, будет началом цикла. Сложность алгоритма — [math]O(n)[/math] . Ниже приведена функция, которая находит эту точку, а возвращает длину хвоста списка.
Рассмотрим цикл длиной [math]N[/math] с хвостом длины [math]L[/math] . Напишем функции для обоих указателей в зависимости от шага [math]n[/math] . Очевидно, что встреча не может произойти при [math]n \leqslant L[/math] , так как в этом случае [math]2n\gt n[/math] для любого [math]n\gt 0[/math] . Тогда положения указателей зададутся следующими функциями (при [math]n\gt L[/math] ):
[math]f_1(n) = L + (n-L) \bmod N[/math]
[math]f_2(n) = L + (2n-L) \bmod N[/math]
Приравнивая, получим [math]n \bmod N = 0[/math] , или [math]n = k N, n \gt L[/math] . Пусть [math]H[/math] — голова списка, [math]X[/math] — точка встречи, [math]A[/math] — первый элемент цикла, [math]Q[/math] — расстояние от [math]X[/math] до [math]A[/math] . Тогда в точку [math]A[/math] можно прийти двумя путями: из [math]H[/math] в [math]A[/math] длиной [math]L[/math] и из [math]H[/math] через [math]X[/math] в [math]A[/math] длиной [math]L + N = X + Q[/math] , то есть:
[math]Q = L + N - X[/math] , но так как [math]X = kN[/math]
[math]Q = L + (1-k) N[/math]
Пусть [math]L = p N + M, 0 \leqslant M \lt N[/math]
[math]L \lt k N \leqslant L + N[/math]
[math]pN + M \lt kN \leqslant (p+1)N + M[/math] откуда [math]k = p + 1[/math]
Подставив полученные значения, получим: [math]Q = pN + M + (1 - p - 1)N = M = L \bmod N[/math] , откуда следует, что если запустить указатели с одной скоростью из [math]H[/math] и [math]X[/math] , то они встретятся через [math]L[/math] шагов в точке [math]A[/math] . К этому времени вышедший из [math]H[/math] пройдёт ровно [math]L[/math] шагов и остановится в [math]A[/math] , вышедший из [math]X[/math] накрутит по циклу [math][L/N][/math] шагов и пройдёт ещё [math]Q = L \bmod N[/math] шагов. Поскольку [math]L = [L/N] + L \bmod N[/math] , то они встретятся как раз в точке [math]A[/math] .
Для того, чтобы обратить список, необходимо пройти по всем элементам этого списка, и все указатели на следующий элемент заменить на предыдущий. Эта рекурсивная функция принимает указатель на голову списка и предыдущий элемент (при запуске указывать [math]NULL[/math] ), а возвращает указатель на новую голову списка.
Алгоритм корректен, поскольку значения элементов в списке не изменяются, а все указатели [math]next[/math] изменят свое направление, не нарушив связности самого списка.

Односвязный список - это совокупность нескольких объектов, каждый из которых представляет собой элемент списка, состоящий из двух частей. Первая часть элемента - значение, которое он хранит, вторая - информация о следующем элементе списка.
Характер информации о следующем элементе зависит от того, где конкретно хранится список. Например, если это оперативная память, то информация будет представлять собой адрес следующего элемента, если файл - позицию следующего элемента в файле. Мы с Вами будем рассматривать реализацию списка хранящегося в оперативной памяти, однако, при желании, вы сможете создать собственный код для хранения списка в файле. Итак, приступим:
Каждый элемент списка мы представим программно с помощью структуры, которая состоит из двух составляющих:
1.Одно или несколько полей, в которых будет содержаться основная информация, предназначенная для хранения.
2. Поле, содержащее указатель на следующий элемент списка.
Отдельные объекты подобной структуры мы далее будем называть узлами, связывая их между собой с помощью полей, содержащих указатели на следующий элемент.
После создания структуры, нам необходимо инкапсулировать её объекты в некий класс, что позволит управлять списком, как цельной конструкцией. В классе будет содержаться два указателя (на хвост, или начало списка и голову, или конец списка), а так же набор функции для работы со списком.
В целом, полученный список можно представить так:
Итак, основные моменты создания списка, мы рассмотрели, переходим непосредственно к его формированию.
Формирование списка. Отведем место для указателей в статической памяти.
Зарезервируем место для динамического объекта.
Присвоим значение переменной ptail, и поместим в информационное поле значение элемента.
Поместим в поле узла адрес еще одного - нового динамического объекта.
Переменная ptail должна содержать адрес последнего добавленного элемента, т. к. он добавлен в конец.
Если требуется завершить построение списка, то в поле указателя последнего элемента нужно поместить NULL.
В результате построен линейный односвязный список, содержащий два узла.
Вставка узла в определенное заданное место списка. Здесь и далее, мы не будем приводить фрагменты кода, так как они являются крупными. Позже мы с вами просто рассмотрим пример реализации односвязного списка целиком. А, сейчас, разберем операции над списком с помощью иллюстраций. Выделить память под новый узел. Записать в новый узел значение. Записать в указатель на следующий узел адрес узла, который должен располагаться после нового узла. Заменить в узле, который будет располагаться перед новым узлом, записанный адрес на адрес нового узла.
Удаление узла из списка. Записать адрес узла, следующего за удаляемым узлом, в указатель на следующий узел в узле, предшествующем удаляемому. Удалить узел, предназначенный для удаления.
Читайте также:


