Как сделать обучающую выборку для нейронной сети
Аннотация научной статьи по компьютерным и информационным наукам, автор научной работы — Галкин В. А., Чернуха С. Н.
Похожие темы научных работ по компьютерным и информационным наукам , автор научной работы — Галкин В. А., Чернуха С. Н.
НАУКА и ОБРАЗОВАНИЕ
Эл № фс 77 - 30569. Государственная регистрация №0421100025. ISSN 1994-0408
77-30569/281808 Алгоритм автоматизированной генерации обучающей выборки для нейросетевого распознавателя рукописных символов.
авторы: Г алкин В. А., Чернуха С. Н.
Введение. При практическом использовании распознавателя рукописных символов важны не только точность и быстродействие распознавания, но и наличие удобного механизма для первоначального обучения распознавателя и его корректировки. Как будет показано в данной статье, нейронной сети недостаточно всего одного или двух примеров начертания каждого символа обучающей выборки для проявления высокой точности распознавания, а необходимость задания большего числа обучающих элементов является обременительной для пользователя.
В данной статье будет рассмотрен метод автоматизированной генерации обучающей выборки для нейронной сети с обратным распространением ошибки, что позволит снизить временные затраты на привлечение человека в качестве учителя для распознавателя рукописных символов.
Элементы обучающей выборки.
Обучающая выборка — это конечное множество объектов, для которых известна их классовая принадлежность, используемое для обучения (тренировки) нейронной сети. При обучении с учителем элементы обучающей выборки подаются на вход нейронной сети. Выходной вектор подстраивается под некоторый заранее заданный целевой вектор путем изменения весов связей нейронной сети. Обучающая выборка не должна содержать противоречий, так как нейронная сеть однозначно сопоставляет выходные значения входным [1].
Рассмотрим зависимость точности распознавания символов от числа элементов обучающей выборки. Для проведения экспериментов будем исследовать способность сети распознавать цифры от 0 до 9.
Исследование будем проводить с применением искусственной трехслойной нейронной сети с логарифмической сигмовидной функцией активации нейронов, обучаемой алгоритмом обратного распространения ошибки. Подробно этот алгоритм описан в [2] и реализован Чернухой С.Н в виде программы на КПК. В задаче on - line распознавания известен путь пера в виде последовательности точек, образующих символ. Для упрощения классификатора количество точек уменьшено до восьми, т.е. символ представляется в виде семи отрезков. Такая выборка делает расстояния между точками практически одинаковыми, что позволяет не учитывать при распознавании размер символа. Для инвариантности символа относительно его положения на изображении, преобразуем входную последовательность в вектор синусов и косинусов углов между осями координат и прямой, соединяющей две соседние точки. Таким образом, на входе нейронной сети имеем 14 значений синусов и косинусов углов значимых отрезков, являющихся нормированными (в диапазоне от -1 до 1), поэтому необходимость наличия обособленного входного слоя отсутствует. Число скрытых слоев равно двум. Для каждого символа формируется своя сеть с одним выходом. Значение на выходе интерпретируется как вероятность (вычисленная с точностью до 0,001) того, что символ, поданный на вход сети является тем символом, на котором была обучена данная сеть.
Обучающая выборка из одного элемента.
: М(-,м. 1Чц Мапа^гигп’
4: 0354*13 5 0г9524941
Чтобы понять, почему распознаватель ведет себя подобным образом, необходимо рассмотреть построенные структуры весов нейронной сети для каждого символа, обратившись к файлам базы данных. Для каждого обученного символа формируются свой набор весов нейронной сети, который сохраняется в XML-файле [3]. Фрагмент такого XML-файла представлен ниже.
В тегах и занесены веса каждого из четырех нейронов ( ) в обоих скрытых слоях, причем согласно выбранной архитектуре сети в первом скрытом слое находится четыре нейрона с 14+1 весами в каждом, а во втором — четыре нейрона с 4+1 весами. Веса единственного нейрона выходного слоя содержатся в теге
Обучающая выборка из двух и более элементов.
Добавим в обучающую выборку, созданную ранее и состоящую из одного элемента на каждый символ, еще по одному элементу. После чего заново обучим сеть.
Вновь проверим точность распознавания, как это было сделано выше.
Точность распознавания немного снижена до 0,967, но остается на допустимом уровне.
При увеличении числа элементов обучающей выборки, адекватность поведения нейронной сети возрастает. Зависимость точности распознавания от числа элементов обучающей выборки представлена ниже.
Обучение нейронной сети- это процесс, в котором параметры нейронной сети настраиваются посредством моделирования среды, в которую эта сеть встроена. Тип обучения определяется способом подстройки параметров. Различают алгоритмы обучения с учителем и без учителя.
Процесс обучения с учителем представляет собой предъявление сети выборки обучающих примеров. Каждый образец подается на входы сети, затем проходит обработку внутри структуры НС, вычисляется выходной сигнал сети, который сравнивается с соответствующим значением целевого вектора, представляющего собой требуемый выход сети.
Для того, чтобы нейронная сети была способна выполнить поставленную задачу, ее необходимо обучить (см. рис. 1). Различают алгоритмы обучения с учителем и без учителя.
Процесс обучения с учителем представляет собой предъявление сети выборки обучающих примеров. Каждый образец подается на входы сети, затем проходит обработку внутри структуры НС, вычисляется выходной сигнал сети, который сравнивается с соответствующим значением целевого вектора, представляющего собой требуемый выход сети. Затем по определенному правилу вычисляется ошибка, и происходит изменение весовых коэффициентов связей внутри сети в зависимости от выбранного алгоритма. Векторы обучающего множества предъявляются последовательно, вычисляются ошибки и веса подстраиваются для каждого вектора до тех пор, пока ошибка по всему обучающему массиву не достигнет приемлемо низкого уровня.
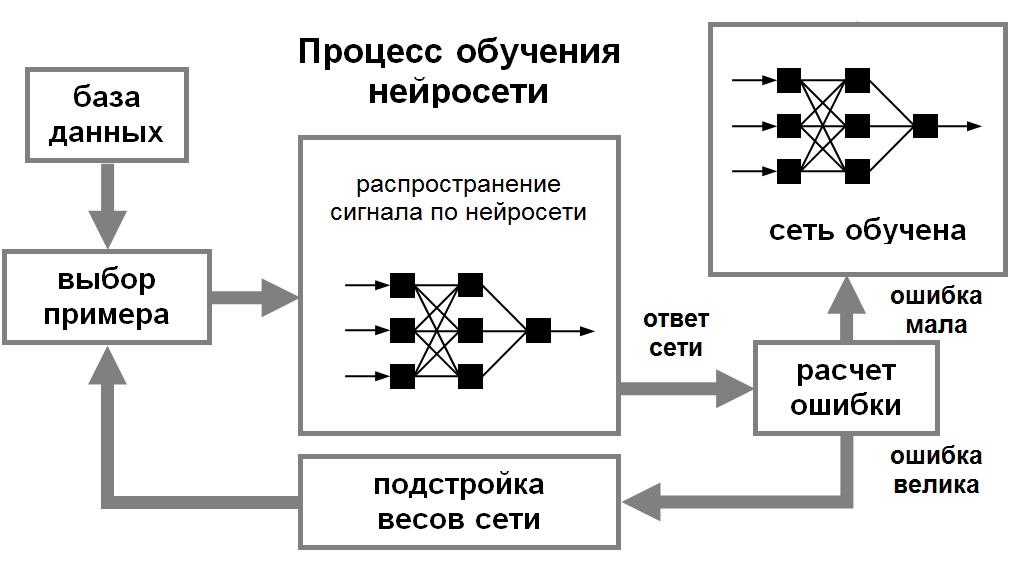
Рис. 1. Иллюстрация процесса обучения НС
При обучении без учителя обучающее множество состоит лишь из входных векторов. Обучающий алгоритм подстраивает веса сети так, чтобы получались согласованные выходные векторы, т.е. чтобы предъявление достаточно близких входных векторов давало одинаковые выходы. Процесс обучения, следовательно, выделяет статистические свойства обучающего множества и группирует сходные векторы в классы. Предъявление на вход вектора из данного класса даст определенный выходной вектор, но до обучения невозможно предсказать, какой выход будет производиться данным классом входных векторов. Следовательно, выходы подобной сети должны трансформироваться в некоторую понятную форму, обусловленную процессом обучения. Это не является серьезной проблемой. Обычно не сложно идентифицировать связь между входом и выходом, установленную сетью.
Для обучения нейронных сетей без учителя применяются сигнальные метод обучения Хебба и Ойа.
Математически процесс обучения можно описать следующим образом. В процессе функционирования нейронная сеть формирует выходной сигнал Y, реализуя некоторую функцию Y = G(X). Если архитектура сети задана, то вид функции G определяется значениями синаптических весов и смещенной сети.
Пусть решением некоторой задачи является функция Y = F(X), заданная параметрами входных-выходных данных (X 1 , Y 1 ), (X 2 , Y 2 ), …, (X N , Y N ), для которых Y k = F(X k ) (k = 1, 2, …, N).
Обучение состоит в поиске (синтезе) функции G, близкой к F в смысле некторой функции ошибки E. (см. рис. 1.8).
Если выбрано множество обучающих примеров – пар (X N , Y N ) (где k = 1, 2, …, N) и способ вычисления функции ошибки E, то обучение нейронной сети превращается в задачу многомерной оптимизации, имеющую очень большую размерность, при этом, поскольку функция E может иметь произвольный вид обучение в общем случае – многоэкстремальная невыпуклая задача оптимизации.
Для решения этой задачи могут использоваться следующие (итерационные) алгоритмы:
алгоритмы локальной оптимизации с вычислением частных производных первого порядка:
градиентный алгоритм (метод наискорейшего спуска),
методы с одномерной и двумерной оптимизацией целевой функции в направлении антиградиента,
метод сопряженных градиентов,
методы, учитывающие направление антиградиента на нескольких шагах алгоритма;
алгоритмы локальной оптимизации с вычислением частных производных первого и второго порядка:
методы оптимизации с разреженными матрицами Гессе,
метод Левенберга-Марквардта и др.;
стохастические алгоритмы оптимизации:
поиск в случайном направлении,
метод Монте-Карло (численный метод статистических испытаний);
алгоритмы глобальной оптимизации (задачи глобальной оптимизации решаются с помощью перебора значений переменных, от которых зависит целевая функция).
На сегодняшний день используются различные алгоритмы обучения нейронных сетей. Каждый из них имеет свои достоинства и недостатки. Но конечная цель – самостоятельное извлечение знаний интеллектуальной системой – так или иначе достигается.
Принцип работы искусственной нейронной сети схож с принципом работы человеческого мозга, но это вовсе не значит, что методы обучения НС будут аналогичными. Тут все же требуются несколько иные подходы к проблеме, о которых мы сегодня и поговорим.
Нейронная сеть и возможность ее обучения
Принцип работы нейронной сети (НС) и ее структура взяты из нейробиологии. Сама идея заключалась в том, чтобы получить математическую модель и ее программное воплощение, которые бы имитировали деятельность человеческого мозга. Разработками в этой области ученые занимаются уже с середины прошлого века. Однако лишь в последние годы развитие нейросетей смогло достичь впечатляющих результатов.
Почему работа в этом направлении так важна? Дело в том, что ни одна вычислительная система не в состоянии воплотить аналитические способности человеческого мозга. Между тем, именно эти качества необходимы программам для решения ряда сложных задач.

Нейронная сеть и возможность ее обучения
В настоящее время нейронные сети используют в следующих направлениях:
- Классификационный анализ — разделение вводных данных по каким-либо признакам. Например, в медицине нейросеть облегчает задачи по диагностике: возраст пациента и его пол, жалобы на здоровье, результаты анализа, записи из анамнеза, реакция на препараты и т.д. – все это позволяет распределить больных по степени тяжести состояния.
- Прогнозирование — с учетом показателей можно спрогнозировать последующие события. Например, каршеринг использует нейросети для выявления агрессивных водителей, чтобы в дальнейшем ограничить им доступ к авто.
- Распознавание образов — это наиболее популярная область для использования нейросетей: идентификация символов на бумаге и банковских картах; распознавание лиц для решения вопросов государственной безопасности; поиск по картинке в Google и прочее.
В основе функционирования искусственного интеллекта лежит машинное обучение. Оно позволяет совершенствовать производительность ИИ без перепрограммирования системы. Говоря простым языком, этот процесс похож на обучение ребенка – он учится классифицировать и распознавать объекты, определять взаимосвязь между ними, и день за днем у него это получается все лучше.
Машинное обучение неразрывно связано с НС и представляет собой работу, при которой смоделированная среда имитирует процессы наработки опыта человеком, постепенно повышая точность результатов.
Ваш Путь в IT начинается здесь
Подробнее
2 типа обучения нейронных сетей
Процесс обучение с учителем
Обучающие примеры поступают в НС в определенной последовательности. Для каждого ответа происходит расчет ошибки и подстройка весов. Все это происходит до тех пор, пока неверные ответы по всему объему обучающего материала не примут значение допустимых показателей.
Обучение с учителем подходит для решения вопросов, в которых известен требуемый результат. Например, для классификации изображений, распознавания звуков или голоса, прогнозирования, функции аппроксимации.
Процесс обучение без учителя

Алгоритмы обучения нейросетей без учителя используют данные без классификации или меток. НС сама выстраивает логическую цепочку и усваивает понимание этих действий, ориентируясь лишь на вводные данные. По сути, это повторяет человеческое самообучение: индивид, предпринимая какие-либо действия, делает выводы о правильности либо ошибочности решения, ориентируясь на последствия.
Обучение без учителя применяют для кластеризации, языковых моделей, обнаружения аномалий, статистических моделей.
3 наиболее распространенных алгоритма обучения нейронных сетей
Выделяют три основных вида алгоритмов обучения нейронных сетей.
Метод обратного распространения
Этот метод также называют Backpropagation. Он является одним из основных способов обучения и содержит в своей основе алгоритм вычисления градиентного спуска. Другими словами, двигаясь вдоль градиента, происходит расчет локального максимума и минимума функции.
Хотите больше зарабатывать или работать удалённо? Запутались в разнообразии профессий и не знаете, куда двигаться?
Команда GeekBrains вместе с экспертами по построению карьеры подготовили документы, которые помогут найти и выбрать востребованную высокооплачиваемую профессию.

Скачивайте и используйте уже сегодня:
Каналы для поиска работы
Список из 26 ресурсов и 34 Telegram-каналов
Топ-30 самых востребованных и высокооплачиваемых профессий 2022
Рейтинг наиболее актуальных специальностей в 9 направлениях
Для лучшего понимания процесса необходимо перевести функцию в график, который будет отображать зависимость значений ошибки от веса синапса. На полученной кривой нужно определить точку с наименьшим и наибольшим показателем. В то же время необходимо графически отобразить все веса, и рассчитать для каждого из них глобальный минимум.
Значение градиента будет иметь векторную величину, которая даст представление о направлении и крутизне склона. Поиск значения градиента осуществляется путем вычисления производной от функции в требуемой точке. Такая точка будет иметь значение веса, распределенное случайным образом. В ней следует проводить расчет градиента и определять направленность движения спуска. Вычисления необходимо производить последовательно во всех точках, пока не будет достигнут локальный минимум, останавливающий дальнейший спуск.
На общую скорость обучения нейросети влияет не только момент ускорения, но и еще одно значение, являющееся гиперпараметром и определяющееся методом подбора.

Метод обратного распространения
Наиболее благоприятное сочетание значений невозможно знать предварительно. Оно выявляется в ходе нескольких обучений и корректировок в нужную сторону.
Как только ответ получен, происходит расчет ошибки, и в соответствии с ней выполняется обратная передача. Цель такого действия – приведение синаптических весов к оптимальным значениям при движении от выходного слоя к входному.
Для такого алгоритма обучения нейронных сетей необходимо использовать дифференцируемые функции активации. Это связано с тем, что распространение в обратном направлении определяется разностью между ответами, а также произведением между ним и производной функцией от входного значения.
Для успешного обучения требуется передать ошибку на все веса НС. При расчете ошибки можно высчитать и дельту на выходном слое. Она будет методично переходить от нейрона к нейрону.
Далее нужно рассчитать градиент для всех исходящих связей. После этого, с учетом полученных данных, требуется провести обновление весов и вычислить величину изменения с помощью функции МОР. Вместе с тем следует помнить о скорости обучения и моменте.
Метод упругого распространения
Этот метод называют также Resilient propagation (сокращенно Rprop). Он был предложен как альтернатива предыдущему способу обучения, который требует слишком много времени и становится неудобным, если результаты нужно получить в короткие сроки. Для увеличения скорости операций было разработано много вспомогательных алгоритмов, в том числе и методика упругого распространения.
Этот метод является основным при обучении по принципу epoch (один полный проход датасета через НС). Для подгонки весовых коэффициентов он использует лишь знаки производных частного случая. При этом обязательно выдерживать правило, позволяющее определить значение коррекции коэффициента веса.

Мы вместе с экспертами по построению карьеры подготовили документы, которые помогут не ошибиться с выбором и определить, какая профессия в IT подходит именно вам.
Благодаря этим гайдам 76% наших студентов смогли найти востребованную профессию своей мечты!
Скоро мы уберем их из открытого доступа, успейте скачать бесплатно:
Гайд по профессиям в IT
5 профессий с данными о навыках и средней заработной плате
100 тыс. руб за 100 дней с новой профессией
Список из 6 востребованных профессий с заработком от 100 тыс. руб
Все профессии, которые есть в IT-сфере
63 профессии и необходимые для них навыки
Критические ошибки, которые могут разрушить карьеру
Собрали 7 типичных ошибок. Их нужно избегать каждому!
Если на этой стадии вычислений производная меняет свой знак на противоположный, то это говорит о чересчур большом изменении и об упущении локального минимума. Следовательно, нужно возвратить весу предыдущее значение и уменьшить величину изменения. Если же знак остался прежним, то следует поднять величину изменения веса для максимальной сходимости.
Если закрепить ключевые показатели подстройки весов, то можно не настраивать глобальные параметры – это является дополнительным плюсом использования метода. Причем существуют готовые значения таких показателей. Их применение рекомендовано, но жестких рамок по выбору значений нет.
Чтобы величина веса не была чрезмерно большой или, наоборот, маленькой, следует оперировать значением коррекции с установленными пределами. При расчете этого значения необходимо придерживаться правила.
В этом случае порядок операций будет таковым:
- определение значения коррекции;
- расчет частных производных;
- расчет новой величины коррекции весовых значений;
- корректировка весов.
Если условие остановки алгоритма не исполняется, то происходит возврат к расчету производных, и цикл запускается по новому кругу.
Благодаря методу упругого распространения сходимость НС добивается в сроки, значительно меньшие, чем при предыдущем алгоритме.
Генетический алгоритм обучения
Еще один распространенный подход – это обучение нейронной сети генетическим алгоритмом (Genetic Algorithm). По своему принципу он схож с эволюционными процессами природы, которые основываются на комбинировании (скрещивании) результатов. Другими словами, происходит естественный отбор, где новое поколение является продуктом комбинации результатов с самыми лучшими свойствами. Если итог такого скрещивания не подходит по каким-то критериям, то отбор совершается вновь, пока продукт не станет совершенным.
Завершение алгоритма происходит в тот момент, когда заканчиваются отведенные ему попытки или время на мутацию. При этом результат может остаться недостигнутым. Данный метод используется для улучшения показателей весов НС при условии, что структура задана по умолчанию. Вес при этом должен быть прописан двоичным кодом, а полный набор веса сформирует итоговый результат. Расчет ошибки на выходе обуславливает оценку эффективности.
В условиях высоких темпов цифровизации общества нейросети являются весьма перспективной областью для развития. Они способны обучиться тем процессам, которые человеческий мозг производит неосознанно, то есть не понимая принципа алгоритма.

Генетический алгоритм обучения
Несмотря на то, что нейронные сети в чем-то повторяют разум человека, нужно понимать, что это лишь искусственное его подобие, но не полноценный эквивалент.
Нейронная сеть из одного нейрона может научиться делать линейную регрессию — находить такую зависимость $y = ax + b$, которая лучше всего описывает данные. Так как формула для перевода градусов Цельсия в Фаренгейты имеет в точности такой вид, то одиночный нейрон должен отлично учиться это делать.
Чтобы обучать и использовать нейронные сети, нужно сначала подготовить вспомогательные функции. Общий план работ:
(если пишете на другом языке, то меняйте всё в соответствии с языком)
A: Цельсии в Фаренгейты
Начнём так, чтобы не перетрудиться сразу. Напишите функцию celsius_to_fahrenheit , которая берёт температуру в градусах Цельсия и возвращает в градусах Фаренгейта. Формулу посмотрите в Википедии, если тестов ниже вам не хватит :)
B: Создание дата-сета
-6.478113785946121 -68.95986937659728 159.64353217340033 388.95577315676417 347.81609825396555 20.339395185296983 -92.1277648778751 319.3583579121206 732.1203916821755 658.0689768571381
Обратите внимание, данные у вас будут другими.
C: Средний квадрат ошибки
Читайте также:


