Как сделать лямбду в маткаде
Пример 1. Составить программу для вычисления корней квадратного уравнения: ax 2 + bx + c = 0 по известной формуле:
Алгоритм (1) является линейным и фрагмент документа MathCAD содержит конструкции, приведенные на рис 1.
П рограммирование разветвляющихся алгоритмов
Характерной чертой разветвляющихся алгоритмов является наличие в них нескольких возможных ветвей вычислений. Выбор конкретной ветви зависит от выполнения (или не выполнения) заданных условий на значения переменных алгоритма.
Пример 2. Значение переменной y зависит от значений переменной x и определяется выражением:
Для реализации разветвляющегося алгоритма необходимо использовать:
· конструкции, проверяющие выполнение заданных условий;
· конструкции, выбирающие нужную ветвь вычислений в зависимости от результатов проверки заданных условий.
Для проверки заданных условий в MathCAD используется: выражение отношений, логические операции и логические выражения.
Выражением отношений (или просто отношением) называется конструкция вида:
где , - произвольные арифметические выражения, - любая из следующих операций: (здесь вертикальные чёрточки являются разделительным символом при перечислении).
Для ввода знаков операций отношений можно использовать палитру Булево (приведённую на рис.3) или использовать клавиши, обозначения которых приведены в таб. 1.

Палитра инструментов БУЛЕВО
Внимание! Не следует путать знак операции сравнения = с похожим знаком вывода значений переменных. Знак операции = имеет больший размер и более жирное начертание.
Выражение отношений принимает одно из двух значений: 1 - если заданное отношение выполняется или 0 – в противном случае. Значение 1 можно интегрировать как значение истина, а 0 – как ложь .
Задание 1 . Пусть значения целой переменной x =3 . Определить значение следующих выражений отношений:
Для проверки более сложных условий используются четыре логических операций, обозначение которых приведены в табл. 2
Таблица 2
Логическое отрицание ( NOT )
Логическое ИЛИ ( OR )
Логическое И ( AND )
Исключающее ИЛИ ( XOR )
Знаки этих операций вводится с палитры Булево . Результат выполнения этих операций, приведен в табл. 3.
Логическим выражением называется конструкция, состоящая из выражений отношений, логических операций и круглых скобок. Логическое выражение принимает только одно из двух значений: 1 или 0; вычисляется слева направо с учетом приоритета входящих в выражение операции. Наивысший приоритет круглые скобки, а затем по убыванию: AND , OR и XOR – одинаковый приоритет и самый низкий приоритет выражения отношений.
Задание 2 . Определите порядок вычисления значений логических выражений в документе MathCAD , приведенных на рисунке 3
Рис. 3 Примеры логических выражений
Пример 2. Записать логическое выражение, принимающее значение 1 при попадании точки с координатами ( x , y ) в первую четверть.
Логическое выражение имеет вид
Для выбора нужной ветви разветвляющегося алгоритма используется конструкция, названная условной функцией if , записывается в виде:
if ( , , ),
где имя функции if вводится с клавиатуры.
Если логическое выражение равно 1, то значение функции определяется выр.1, в противном случае – выр. 2. Блок-схема этой функции приведена на рис. 4.
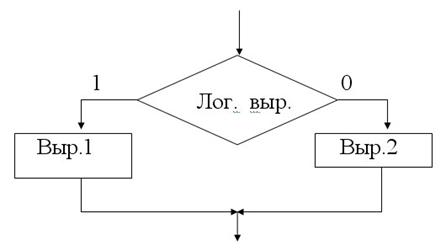
Рис. 4. Блок-схема функции if
При программировании разветвляющихся алгоритмов с тремя и более вычислительных ветвей на месте выр. 1 и выр. 2 вновь может использоваться функция if .
Пример 3. Используя условную функцию if запрограммировать два разветвляющихся алгоритма:
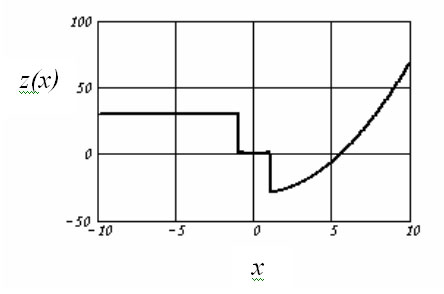
Рис. 5. Реализация разветвляющихся алгоритмов
В MathCAD имеется ряд встроенных функций, которые возвращают результат, зависящий от знака или величины аргумента и которые могут использоваться при программировании разветвляющихся алгоритмов. Приведем некоторые из них:
· ceil ( x ) – наименьшее целое, большее или равное x ;
· trunc ( x ) – целая часть вещественного числа x ;
· floor ( x ) – наибольшее целое, меньшее или равное x ;
· round ( x , n ) – округленное значение вещественного x с точностью до n знаков после десятичной точки;
· Ф( x ) – функция Хевисайда – равна 0 при x и 1 в противном случае;
· sign ( x ) – функция знака (равна 0 если x = 0; -1, если x и 1 , если x >0 );
· signum ( x ) – возвращает 1, если x = 0 и в остальных случаях.
Программирование циклических алгоритмов
Типы циклов. П о способам организации цикла можно выделить:
а) цикл типа арифметической прогрессии;
б) итерационный цикл.
Программирование цикла типа арифметической прогрессии
Особенностью цикла типа арифметической прогрессии является изменение параметра цикла по закону арифметической прогрессии и поэтому можно, не выполняя цикла, определить количество повторений цикла.
Параметр такого цикла задается дискретной переменной и тогда конструкции, входящие в тело цикла располагаются, начиная от этого описания и до конца документа MathCAD или до конструкции, переопределяющей дискретную переменную – параметр цикла.
Этот цикл имеет уже два параметра: i – параметр, определяющий номер строки; j – параметр, определяющий номер столбца матрицы. Заметим, что такой цикл называется двойным циклом.
Заметим, что если параметр цикла не входит в индексные выражения элементов массива, то он может принимать вещественные значения.
Заметим, что во фрагментах, приведенных на рисунках системная переменная ORIGIN =1.
Система MathCAD содержит большой набор встроенных элементарных функций. Функции задаются своими именами и значениями аргумента, заключёнными в круглых скобках. Функции, как и переменные, и числа, могут входить в состав математических выражений. В ответ на обращение к ним, функции возвращают вычисленные значения. Ниже представлены некоторые из этих функций.
1.2.1 Тригонометрические функции
sin (z) - синус . cos (z) - косинус
tan (z) - тангенс . sec (z) - секанс
csc (z) - косеканс . cot (z) - котангенс
1.2.2 Гиперболические функции
sinh (z) - гиперболический синус
cosh(z) - гиперболический косинус
tanh(z) - гиперболический тангенс
sech(z) - гиперболический секанс
csch(z) - гиперболический косеканс
coth(z) - гиперболический котангенс
1.2.3 Обратные тригонометрические функции
asin (z) - арксинус
acos(z) - арккосинус
atan(z) - арктангенс
1.2.3 Обратные тригонометрические функции
asin (z) - арксинус
acos(z) - арккосинус
atan(z) - арктангенс
1.2.4 Обратные гиперболические функции
asinh (z) - обратный гиперболический синус
acosh(z) - обратный гиперболический косинус
atanh(z) - обратный гиперболический тангенс
1.2.5 Показательные и логарифмические функции
exp (z) - экспоненциальная функция
ln (z) - натуральный логарифм
log (z) - десятичный логарифм
1.2.6 Функции с условиями сравнения
ceil (x) - наименьшее целое, большее или равное х
floor(x) - наибольшее целое, меньшее или равное х
mod(x,y) - остаток отделения х/у со знаком х
angle(x,y) - положительный угол с осью х для точки с координатами (х,у)
Но задать ее не могу (Mathcad 15). Он просто пишет две точки и все.
Но при этом могу задавать перечислением:
Но при подстановке в функцию f(x) происходит ошибка: пишет что значение должно быть скалярным.
Хотя в видеоуроках все норм и выдается таблица значений при различных приближениях х.
Помогите плз разобраться!
Как задать интервал без шага
Здравствуйте. Такой вопрос : как переменной присвоить произвольные значения, (наподобие массивов в.
Как задать интервал с отрицательными и положительными значениями
Доброго времени суток. Подскажите как задать интервал в Mathcad с отрицательными и положительными.
Как можно задать интервал, чтобы отображалось 2 одинаковых значения
Здравствуйте, подскажите как можно задать интервал, чтобы отображалось 2 одинаковых значения (на.
Как задать интервал функции x в Gnuplot
Всем привет! Подскажите пожалуйста как задать интервал функции x в гнуплоте. Не осей, а именно.
В этой статье мы подробно разберем, как в MathCAD задать интервал с определенным шагом.
MathCAD интервал значений
Для начала вспомним: чтобы задать диапазон значений с шагом 1 по умолчанию вводим переменную, которой мы задаем значение (у меня это будет х), затем ставим знак присвоение



Однако, использовать эти значения в выражениях не получится, т.к. MathCAD определяет их как не скалярную величину

В то же время, простое вычисление вполне можно произвести



Конечно, это несколько, не удобно, особенно, если брать большие интервалы, или интервалы далеко от нуля. Можно вызывать значение отдельного значения интервала, задав необходимый индекс (на клавиатуре наберем z[2= ).
MathCAD интервал с заданным шагом
По умолчанию шаг интервала в MathCAD принят за единицу, чтобы его сделать другим необходимо задать интервал следующим образом: а:=0.2,0.4..2 (этим выражением мы задаем интервал от 0,2 до 2 с шагом 0,2)
Урок 7. Переменные-диапазоны и графики в Mathcad
Переменные-диапазоны имеют множество значений. На рисунке Вы видите определение и вывод двух переменных-диапазонов.

Для первой переменной начальное значение равно 0, конечное – 3, а шаг равен 1. Для второй переменной первое значение определено 3, второе – 6, а верхняя граница равна 13. Первая переменная-диапазон i создана как математическая область с помощью оператора [..]:
Для ввода этого выражения наберите [i:0..3].
Вторая переменная j определяется в два шага:
- Введите [j:3,], и после запятой появится местозаполнитель
Первый тип переменной-диапазона, с шагом 1, наиболее часто используем. При необходимости, эту переменную можно изменить:

Можно использовать параметры в определении переменной-диапазона. В следующем примере с помощью параметра можно изменять длину переменной-диапазона:

Второй метод определения более гибок. В местозаполнитель, который появляется после запятой, вводится второе значение переменной-диапазона (не шаг увеличения). Во второй местозаполнитель вводится верхняя граница: значения переменной-диапазона закончатся на этой границе или до нее:

Если переменная-диапазон используется в качестве индекса массива, то ее элементы должны быть натуральными числами или нулем.
Наша функция
Мы вычислим нашу функцию для шести значений переменной-диапазона:
(Ряд 0, 1, 2, 3, 4, 5 включает в себя шесть значений.) Определим шесть значений переменной x (подстрочный индекс – с помощью [):
С помощью подстрочных индексов можно проверить значения:

Теперь определим и проверим значения функции:

Для проверки всех значений наберите [x=] и [y=]:

Это векторы – мы их подробно обсудим в уроке 22.
Первый график
Теперь значения x и y можно вывести на график. Нажмите Графики –> Вставить график –> График XY

Появятся оси. В местозаполнитель введите y:

Щелкните по местозаполнителю внизу, введите [x] и нажмите [Enter]. Появится график:

Элементы графика
Элементы графика показаны на рисунке внизу. Этими элементами являются:
- Две оси: ось X и ось Y.
- Легенды осей X и Y.
- Фон графика.
- Линия графика.
- Метки на осях.
- Значения на метках.

Выберите созданный график щелчком с зажатой клавишей [Ctrl]. Подведите курсор к правому нижнему углу – он изменится на двойную стрелку. Щелкните мышью и перемещайте курсор для изменения размеров области. Установите такой размер, который Вам больше подходит. Теперь подведите курсор на горизонтальную ось X. С помощью двойной стрелки Вы можете перемещать ее вверх и вниз. Вертикальную ось Y можно перемещать аналогичным образом в горизонтальном направлении. Фон графика можно изменить с помощью вкладки График –> Фон графика. Выберите тип фона Прозрачный.
Мы посчитали и вывели на график лишь несколько точек, поэтому график получился несглаженным. Возможно, лучше вывести на график только точки. Выберите Графики –> Стили –> Символ и выберите круг – третий символ в списке. На линии появятся символы:

Выберите Стиль линии –> (нет), и линия исчезнет. Поскольку символы малы, увеличьте толщину кривой (размер символов также увеличится). Измените также цвет кривой на красный:

Теперь обратите внимание на метки и значения возле них. Медленно проведите указатель мыши по меткам вдоль оси Y. Значения на первой, второй и последней метки увеличатся при наведении на них указателя. Их можно изменить. Первое и последнее значение определяют границы вывода графика. С помощью второго значения можно изменять число меток на оси. Измените значение на второй метке на оси Y на 5 вместо 2.5, а на оси X – на 1 вместо 0.5:

Выберите график, затем щелкните по вкладке График –> Оси –> Выражения оси. При щелчке вне графика легенда исчезнет (она появится, если Вы щелкните по графику). На рисунке вместо легенды размещены две маленькие математические области с y и x:

Полученный в результате график, возможно, выглядит лучше, чем изначальный, но это дело вкуса.
Быстрое построение графика
Есть способ построить график быстрее, если Вы хотите увидеть лишь поведение функции. Перед тем, как сделать это, удалите предыдущие значения переменной x с помощью команды clear(x):
Функция, график которой нужно построить:
Вставьте график XY. Введите [y(x] в первый местозаполнитель и [x] во второй. Затем щелкните вне графика. Диапазон x обычно выставляется от -10 до 10. Диапазон по y выбирается автоматически:
Система MathCAD содержит большой набор встроенных элементарных функций. Функции задаются своими именами и значениями аргумента, заключёнными в круглых скобках. Функции, как и переменные, и числа, могут входить в состав математических выражений. В ответ на обращение к ним, функции возвращают вычисленные значения. Ниже представлены некоторые из этих функций.
1.2.1 Тригонометрические функции
sin (z) - синус . cos (z) - косинус
tan (z) - тангенс . sec (z) - секанс
csc (z) - косеканс . cot (z) - котангенс
1.2.2 Гиперболические функции
sinh (z) - гиперболический синус
cosh(z) - гиперболический косинус
tanh(z) - гиперболический тангенс
sech(z) - гиперболический секанс
csch(z) - гиперболический косеканс
coth(z) - гиперболический котангенс
1.2.3 Обратные тригонометрические функции
asin (z) - арксинус
acos(z) - арккосинус
atan(z) - арктангенс
1.2.3 Обратные тригонометрические функции
asin (z) - арксинус
acos(z) - арккосинус
atan(z) - арктангенс
1.2.4 Обратные гиперболические функции
asinh (z) - обратный гиперболический синус
acosh(z) - обратный гиперболический косинус
atanh(z) - обратный гиперболический тангенс
1.2.5 Показательные и логарифмические функции
exp (z) - экспоненциальная функция
ln (z) - натуральный логарифм
log (z) - десятичный логарифм
1.2.6 Функции с условиями сравнения
ceil (x) - наименьшее целое, большее или равное х
floor(x) - наибольшее целое, меньшее или равное х
mod(x,y) - остаток отделения х/у со знаком х
angle(x,y) - положительный угол с осью х для точки с координатами (х,у)
Читайте также:


