Как сделать круг в графике

Обновлено: 08.01.2025

В этом уроке мы разберемся, как изображать объекты, в основе которых лежат окружности: чайник, вазу, бокал, кувшин, колонну, маяк. Сложность их изображения в пространстве заключается в том, что принцип равноудаленности точек окружности от центра срабатывает, только когда мы смотрим на плоскость прямо (то есть направление взгляда перпендикулярно ей). Например, мы видим круглый циферблат часов перед собой или чашку и блюдце, когда наклонились над ними. В других случаях (взгляд падает на плоскость под углом) мы видим искажение формы окружности, ее превращение в овал (эллипс).

Содержание:

Ненадолго вернемся к коробкам из прошлого урока. Только теперь рассмотрим кубическую форму. Обратите внимание, как квадраты плоскостей, уходящих вдаль, сплющиваются. Верхние и нижние грани превращаются в трапеции. И тем сильнее они сужаются по вертикальной оси, чем ближе находятся к уровню глаз (к линии горизонта).

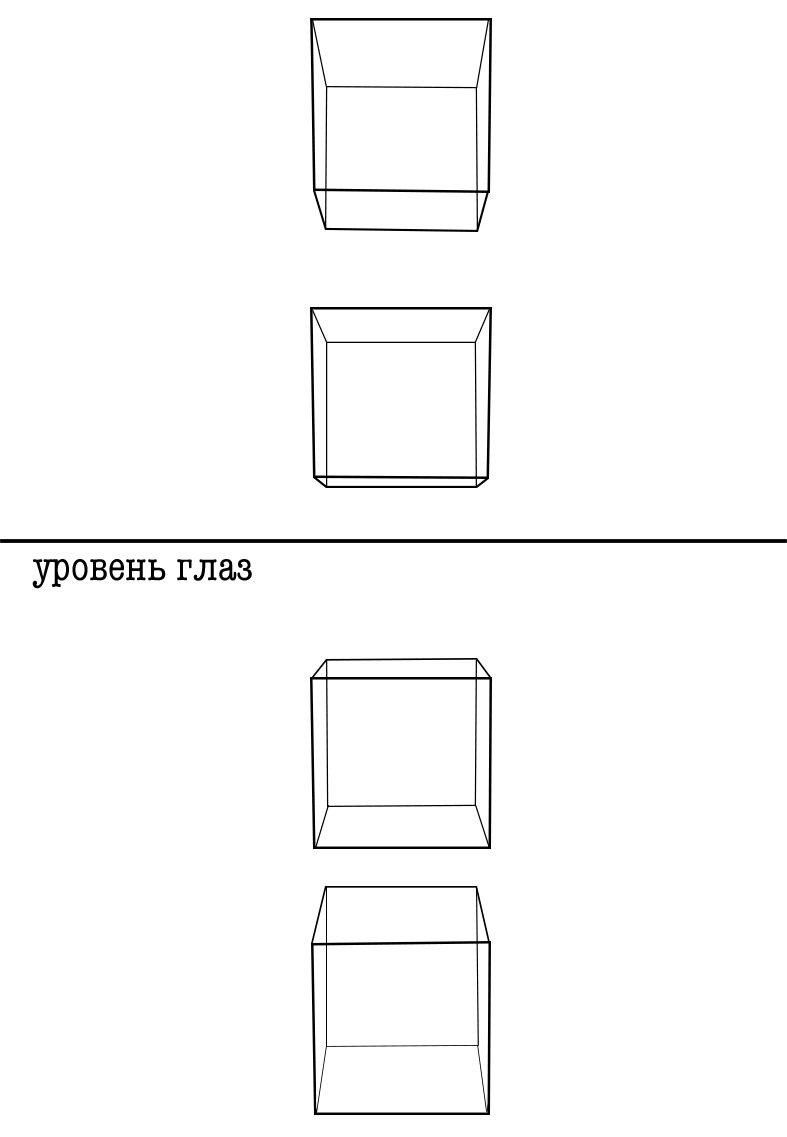
То же самое происходит и с окружностями. Чем дальше от линии горизонта они находятся, тем больше они открываются (обратите внимание на верхние и нижние плоскости этих спилов). А на уровне глаз окружность сужается до линии. Мы видим лишь переднюю грань предмета.

Принципы рисования эллипсов:

Принцип 1. У эллипса есть две оси симметрии: большая и малая. Они перпендикулярны. Здесь будем работать с наиболее частым случаем – когда предмет расположен прямо, то есть вертикальная ось (малая) находится под углом в 90°, а горизонтальная (большая) – под углом в 180°.

Принцип 2. У эллипса 4 вершины (они лежат на пересечении с осями). Эти точки в наибольшей степени удалены от центра. Форма эллипса выглядит искаженной, если соседние с вершинами точки смещены на тот же уровень (на эллипсе справа показано красным цветом).

Принцип 3. Другая крайность – это заострение боков эллипсов. Они должны быть скругленными. В бока можно вписать окружности. И чем больше раскрыт эллипс, тем больше диаметр этой окружности относительно высоты эллипса (на примере ниже это сравнение показано бледно-голубым цветом).

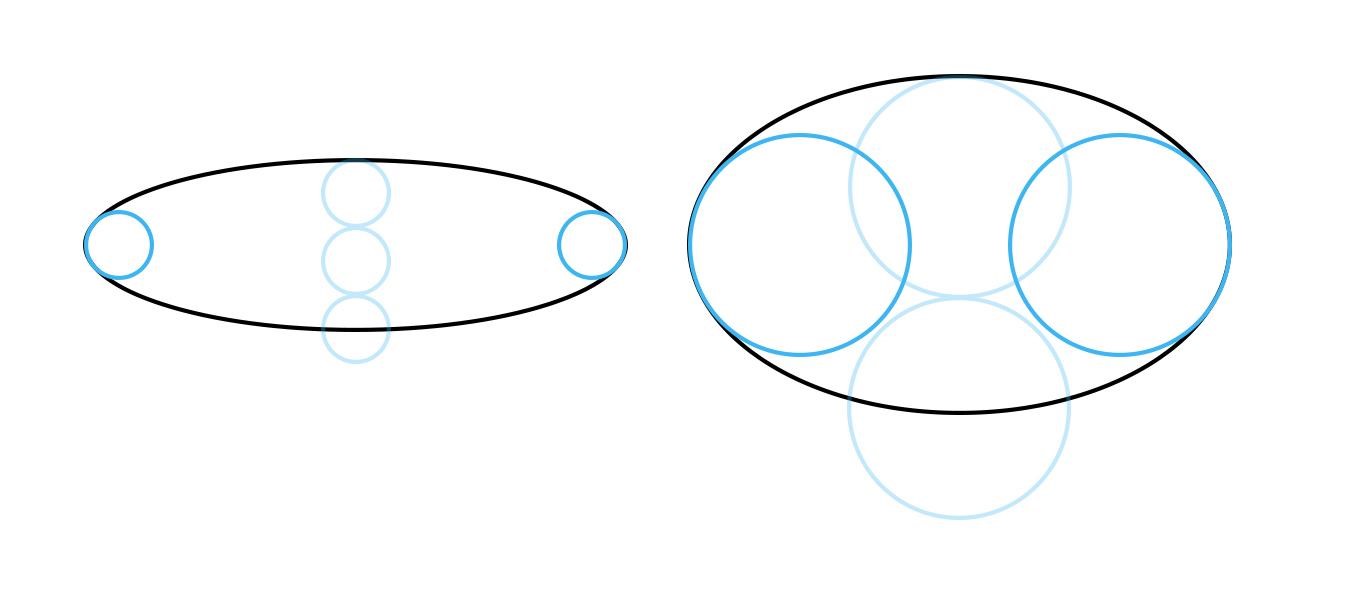
Принцип 4. Центр эллипса смещен вдаль (вверх) относительно геометрического центра из-за перспективного искажения. То есть ближняя половина эллипса больше дальней. Однако обратите внимание, что это смещение очень незначительно. Разберем, почему. Начнем с квадратов, поскольку круг вписывается в эту форму. Ниже показаны кубы, справа их верхние квадратные грани в перспективе. Проведены оси красным. Сравните, насколько их ближние половины больше дальних. Разница очень небольшая. То же самое будет и для эллипсов, вписанных в них. Ошибочно преувеличивать в рисунках эту разницу между ближней и дальней половинками эллипсов.

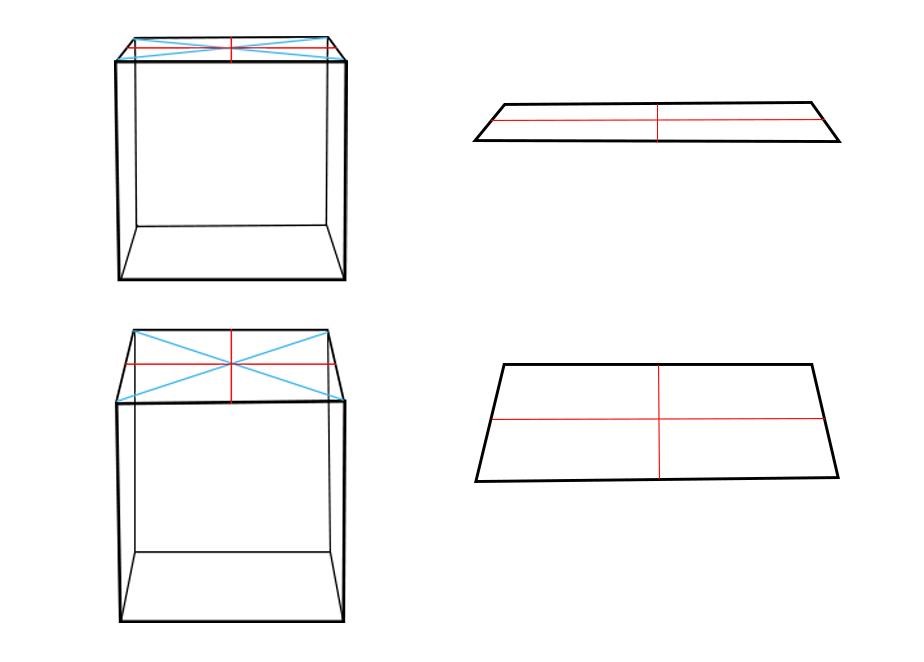
Рисуем эллипсы

Шаг 1. Для начала проведем две перпендикулярных оси.

Шаг 2. Отметим границы произвольного эллипса симметрично по горизонтальной оси. А для вертикальной верхнюю половину (дальнюю) сделаем чуть-чуть меньше нижней.

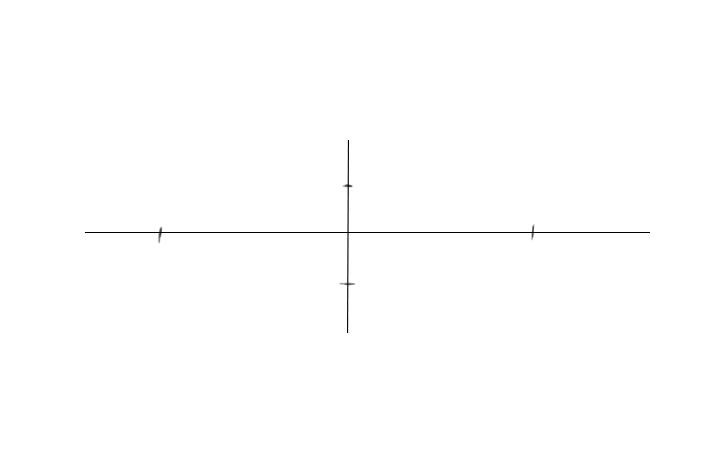
Шаг 3. Нарисуем по этим отметкам прямоугольник, в который будем вписывать эллипс.

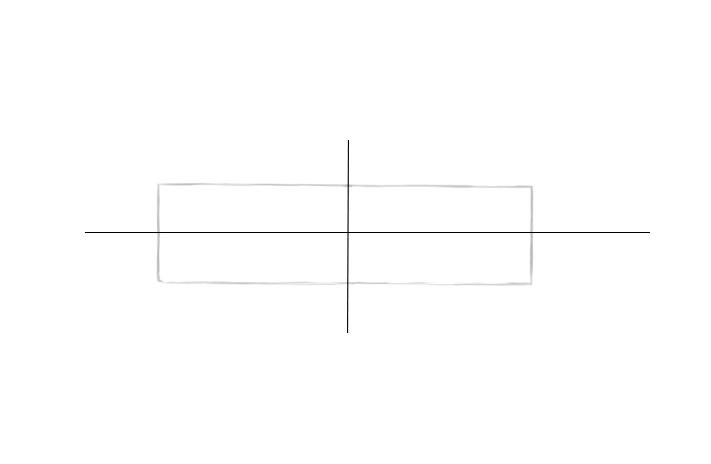
Шаг 4. Наметим легкие дуги в местах пересечения осей и прямоугольника.

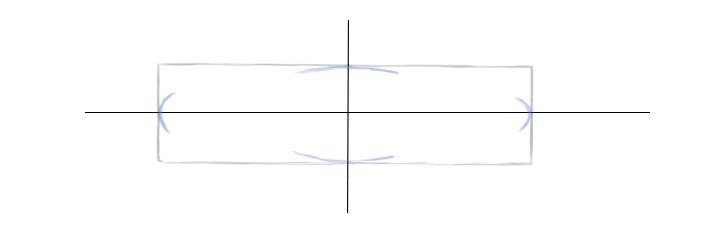
Шаг 5. Соединим легкими линиями эти дуги, стараясь изобразить эллипс более симметрично.

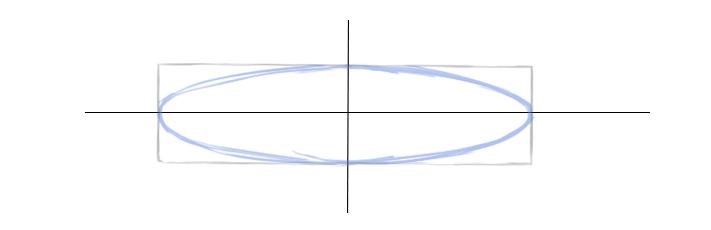
Шаг 6. По обозначенному пути проведем более четкую линию. Смягчим ластиком лишнее.

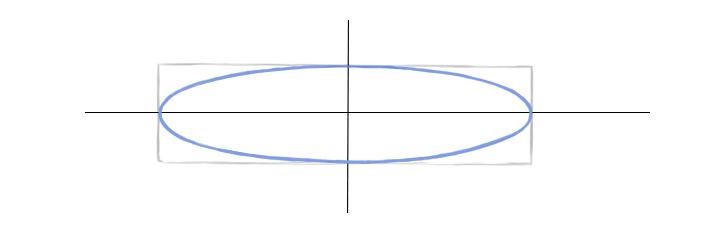
Более правильно было бы при рисовании эллипса вписывать его в квадратную плоскость в перспективе, то есть в трапецию. Однако, во-первых, сложно точно построить такую трапецию, зная лишь вершины эллипса. А во-вторых, овал, вписанный в квадрат в перспективе, мало отличается от вписанного в прямоугольник по тем же самым вершинам.

Рисуем кружку

Шаг 1. Начинаем с общих пропорций предмета. Измеряем, сколько раз ширина кружки (ее верха) умещается в высоте. Можно пока не учитывать ручку, однако надо оставить для нее достаточно места на листе. Намечаем общие габариты. Находим середину предмета по ширине и проводим через нее вертикальную ось. Чтобы нарисовать ее ровно, удобно сделать 2-3 вспомогательные отметки по высоте предмета на том же расстоянии от ближнего края листа, что и первая отметка середины предмета.

Шаг 2. Найдем высоту верхнего эллипса. Для этого измерим, сколько раз она умещается в его ширине (которую мы нашли ранее). Отметим нижнюю границу эллипса от верхнего края кружки. Легкими линиями нарисуем прямоугольник по намеченным крайним точкам.

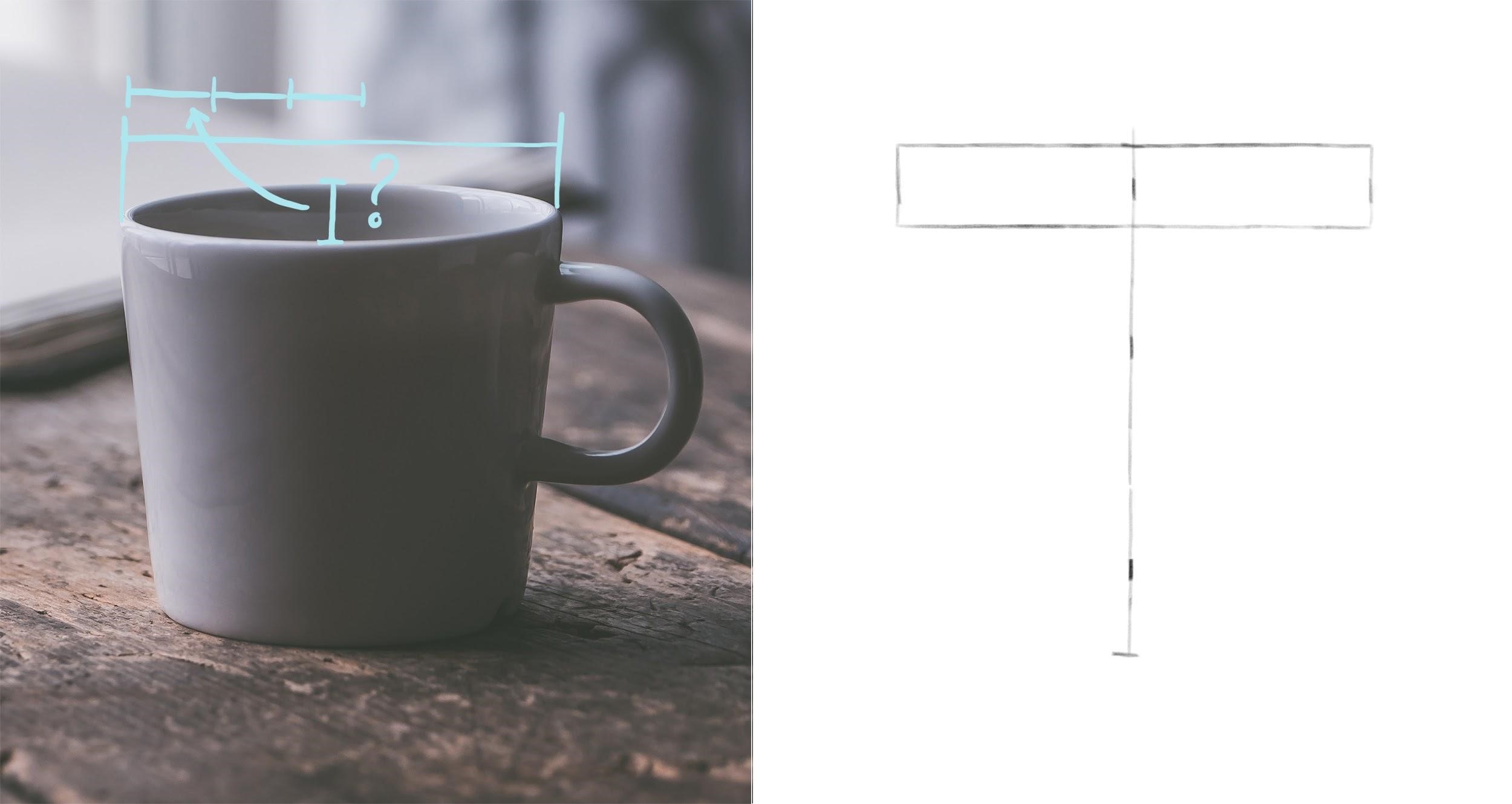
Шаг 3. Проведем горизонтальную ось и впишем эллипс в прямоугольник. Затем найдем ширину нижней части кружки, сравнив ее с шириной верха. Высоту нижнего эллипса мы найдем, измерив расстояние по вертикали от самой нижней отметки кружки до нижней отметки ее бока (до точки, через которую пройдет горизонтальная ось этого эллипса). Найденное расстояние – это половина искомой высоты. Удвоим его и отложим от самой нижней точки кружки. Здесь важно не запутаться: в данном случае ось надо провести через нижнюю точку бока кружки, а не через низ самой кружки. Иначе пропорции нарушатся. Зная высоту нижнего эллипса, проверим, соблюдается ли принцип их постепенного раскрытия по мере удаления от уровня глаз. Верхний эллипс расположен ближе к уровню наших глаз, чем нижний, поэтому должен быть уже. Найдем, сколько раз высота нижнего овала помещается в его ширине – около четырех раз. Для верхнего овала было соотношение примерно 5 к 1. Таким образом нижний овал шире, то есть раскрыт в большей степени. Принцип соблюдается.

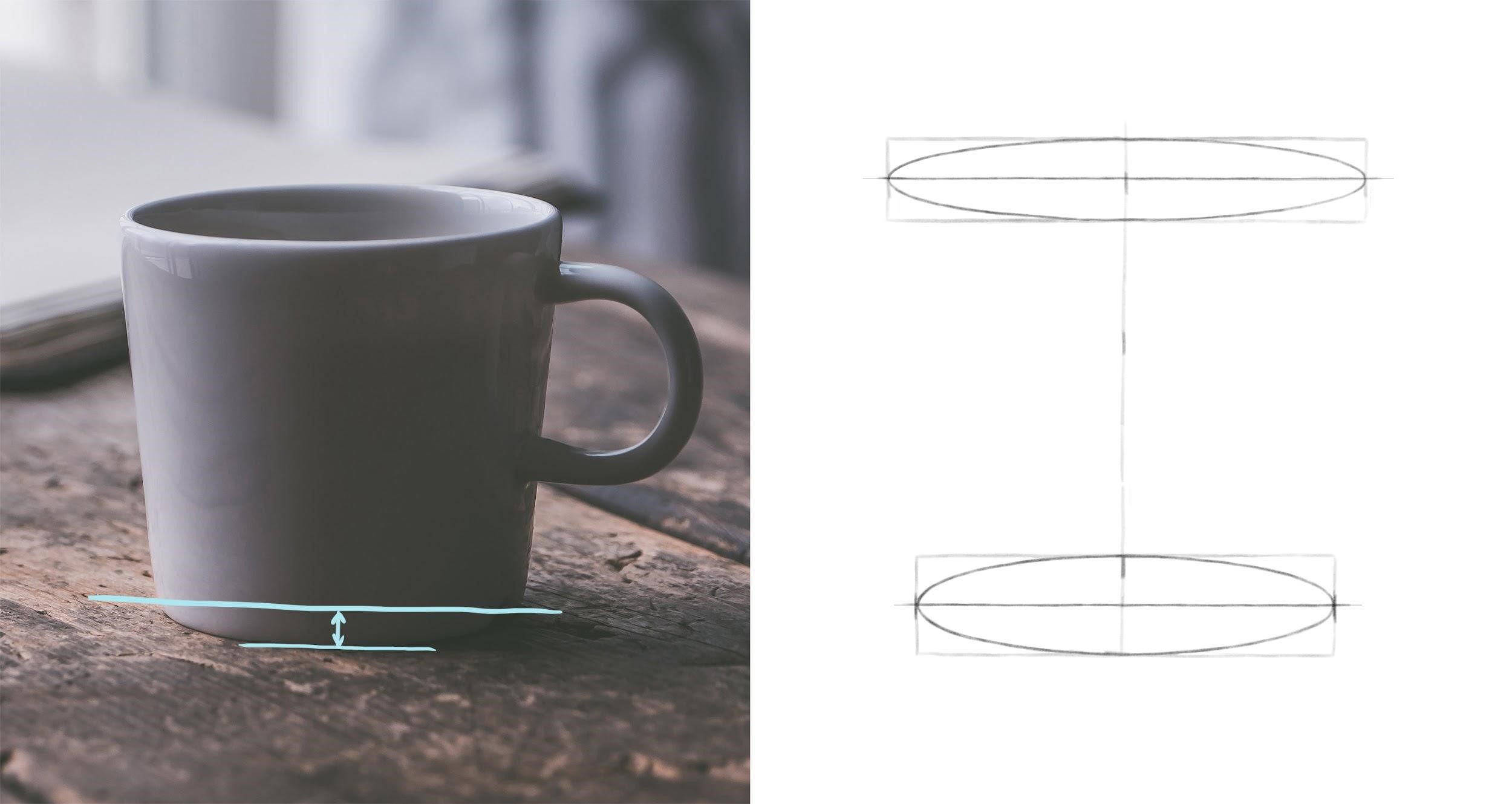
Шаг 4. Рисуем стенки кружки, соединяя боковые вершины верхнего и нижнего эллипсов. Для большей объемности покажем толщину стенки. Нарисуем второй овал внутри верхнего. При этом учитываем, что из-за перспективного искажения толщина стенок выглядит не одинаковой. Передняя и дальняя стенки визуально сужаются сильнее боковых примерно в два раза. Отметим вершины внутреннего овала на некотором расстоянии от вершин первого овала. Делаем этот отступ чуть больше для боковых вершин. Ставим отметки симметрично относительно вертикальной и горизонтальной осей. Нарисуем новый эллипс через эти вершины.

Шаг 5. Найдем расположение ручки и ее общие пропорции, а затем схематично наметим основные отрезки, формирующие ее контур. Их наклоны определяем методом визирования (а где-то - на глаз).

Шаг 6. Уточним контур ручки, сделаем его более плавным. По необходимости подправим очертания кружки. Смягчим немного ластиком линии построения. Выделим более сильным нажимом на карандаш контуры, расположенные ближе к нам. Кружка готова!

Рисуем вазу

В этом упражнении поработаем с воображением. Придумаем свою вазу и потренируемся рисовать эллипсы.

В прошлом задании для построения кружки было достаточно нарисовать два эллипса. Две ключевые окружности (верхняя и нижняя) определяли ее форму. Диаметр кружки равномерно уменьшался от верха к низу. А, например, форма вазы из рисунка ниже зависит от четырех окружностей (причем верхняя находится на уровне глаз, поэтому превратилась в линию).

Перейдем к рисованию. И помним важный принцип: чем дальше эллипс от уровня глаз, тем более он раскрыт.

Шаг 1. Проведем вертикальную ось. От нее симметрично отложим горизонтальные оси будущих эллипсов. Длину вертикальной и горизонтальных осей, а также количество эллипсов и расстояние между ними выбирайте сами.

Шаг 2. Обозначим боковые вершины эллипсов симметрично относительно вертикальной оси. Теперь перейдем к обозначению верхних и нижних вершин. И здесь пользуемся принципом постепенного раскрытия эллипсов по мере удаления от линии горизонта. Например, здесь мы рисовали вазу, расположенную в целом ниже уровня глаз. Для первого эллипса взяли высоту, примерно в пять раз меньше ширины. Измеряли это карандашом. Для последующих эллипсов постепенно увеличивали степень раскрытия. Так высота среднего эллипса укладывается в ширине примерно четыре раза, а для самого нижнего – примерно три раза. Чем ближе друг к другу эллипсы, тем ближе они по степени раскрытия. Чем дальше – тем больше разница. Намечая вершины, нижнюю половинку (ближнюю) делаем чуть-чуть больше верхней (дальней).

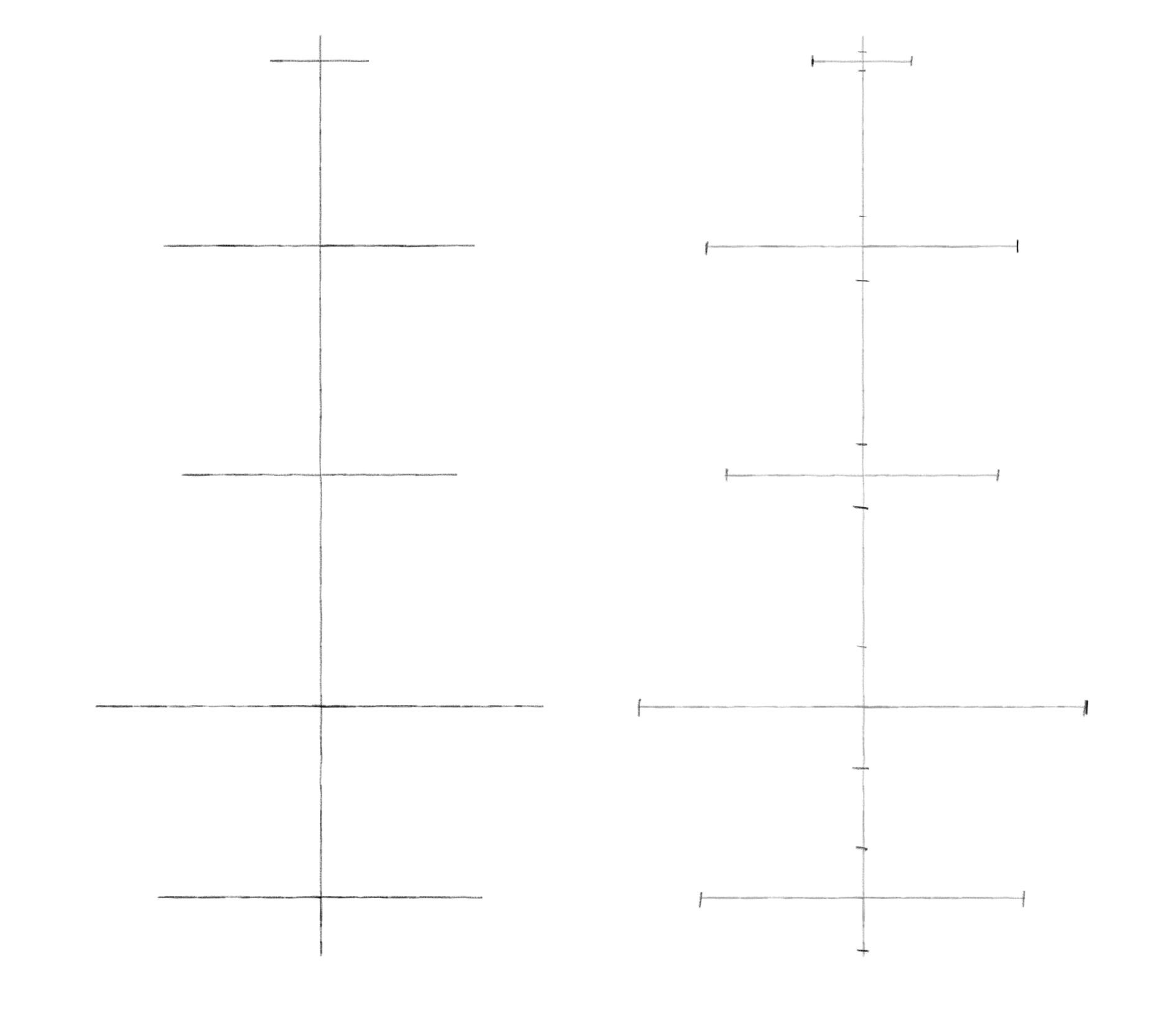
Шаг 3. Через вершины легкими линиями рисуем прямоугольники. А затем вписываем в них эллипсы.

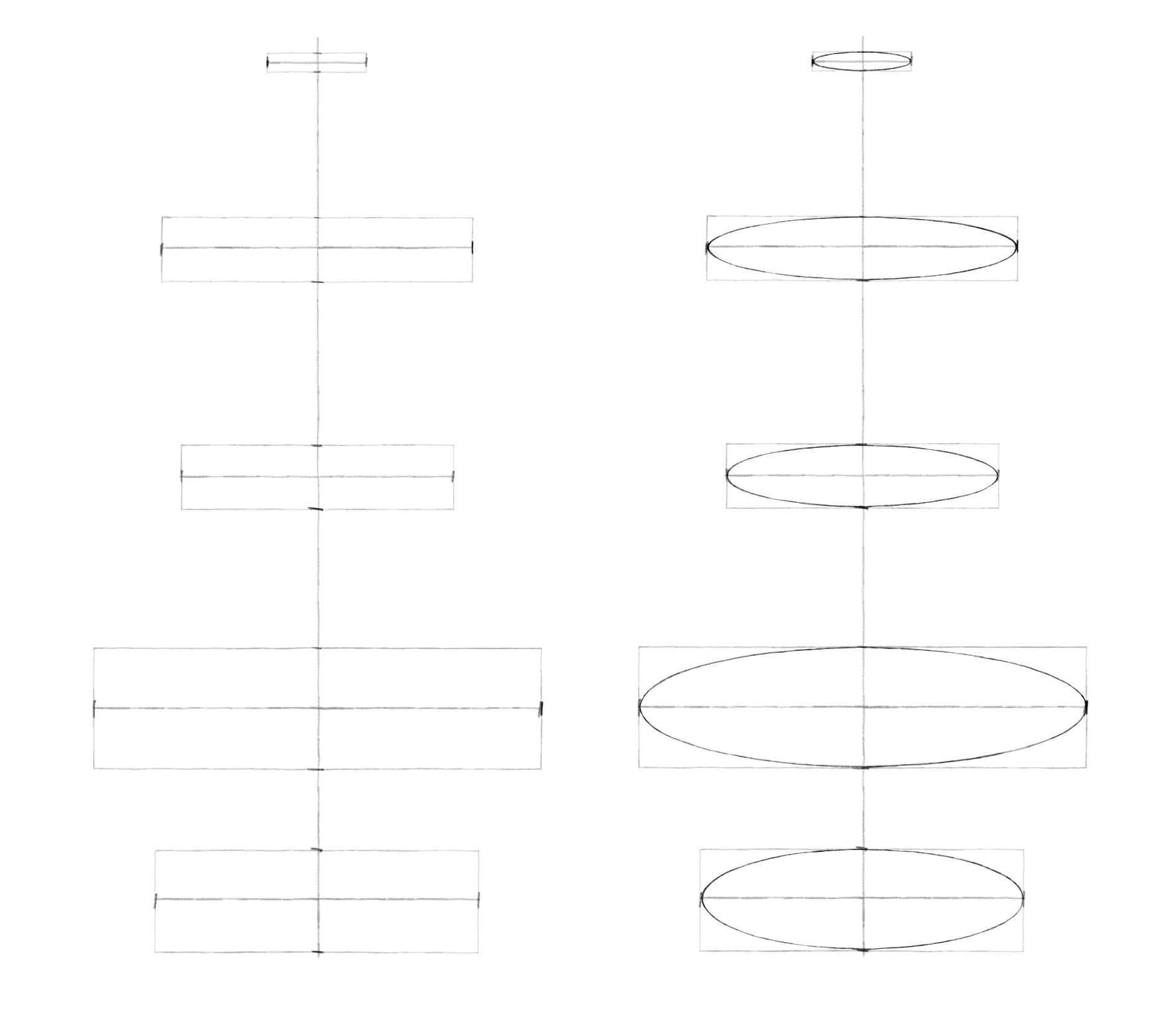
Шаг 4. Теперь самое интересное: надо соединить боковые вершины эллипсов линиями. Вам решать, какими они будут, прямыми или округлыми, вогнутыми или выпуклыми. Можно сделать пару вариантов. Постарайтесь наиболее симметрично повторить форму внешнего контура для двух половинок вазы. Чтобы проверить симметрию, пробуйте перевернуть работу вверх ногами. Взглянув на предмет по-новому, проще увидеть расхождения.

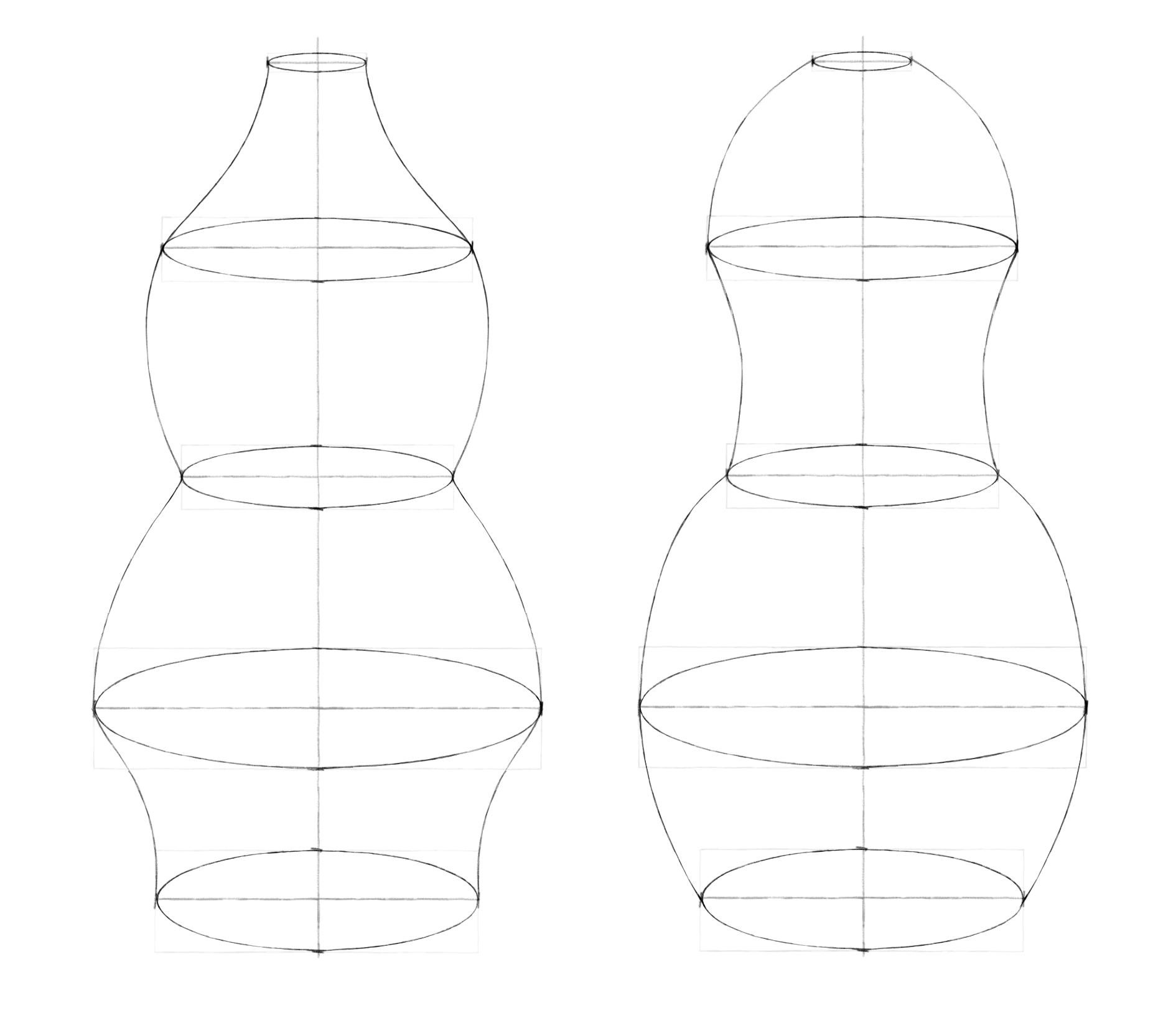
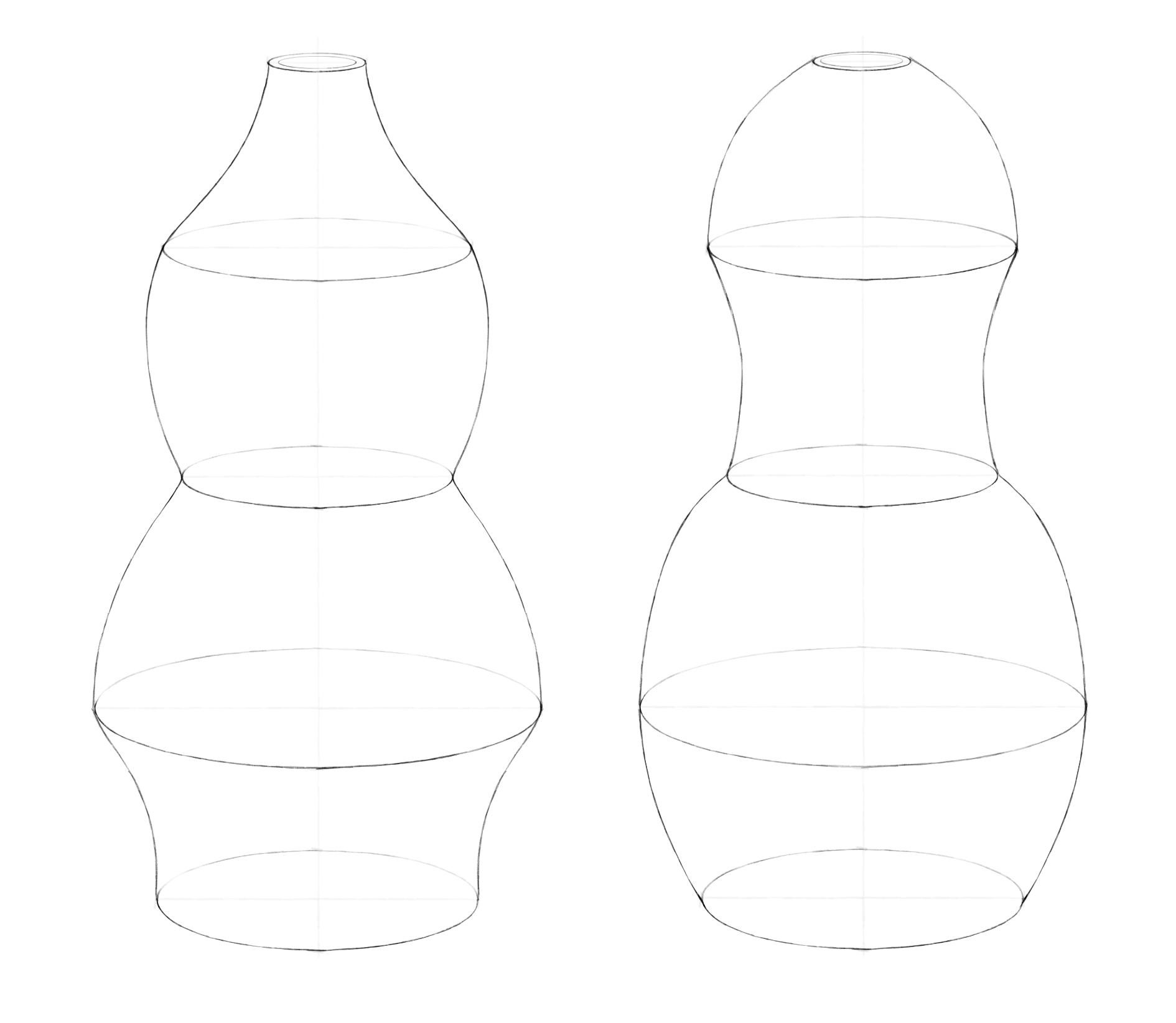
Шаг 5. Так же, как мы делали для кружки, здесь можно показать толщину стенки. Нарисуем внутри верхнего эллипса еще один поменьше, предварительно наметив его вершины. Смягчим ластиком оси и дальние половинки эллипсов. Можно чуть высветлить те эллипсы, в которых изменение формы вазы более плавное. Рисунок готов!

Проверьте свои знания

Для работы с графикой в pascal abc используется модуль GraphABC. Для его подключения используется следующий код:

uses GraphABC; begin . end.

Система координат в Паскале соответствует экранной системе координат и выглядит следующим образом:

Управление цветом

Для того, чтобы использовать цвет, необходимо применить этот цвет к инструменту перо:

• SetPenColor(color) — устанавливает цвет пера, задаваемый параметром color;
• setBrushColor(color) — устанавливает цвет кисти, задаваемый параметром color;
• либо для палитры RGB: SetPenColor(rgb(0-255, 0-255, 0-255));

или использовать для заливки:

После чего можно использовать процедуры для рисования геометрических фигур.

clBlack – черный
clPurple – фиолетовый
clWhite – белый
clMaroon – темно-красный
clRed – красный
clNavy – темно-синий
clGreen – зеленый
clBrown – коричневый
clBlue – синий
clSkyBlue – голубой
clYellow – желтый
clCream – кремовый
clAqua – бирюзовый
clOlive – оливковый
clFuchsia – сиреневый
clTeal – сине-зеленый
clGray – темно-серый
clLime – ярко-зеленый
clMoneyGreen – цвет зеленых денег
clLtGray – светло-серый
clDkGray – темно-серый
clMedGray – серый
clSilver – серебряный

Точки, отрезки и ломаные

Для отображения точки в паскале используется процедура:

uses GraphABC; begin SetPixel(300,200,clred); end.

Для рисования линии используется:

uses GraphABC; begin SetPenColor(clgreen); line(100,50,500,250); end.

Ломаные можно рисовать с помощью процедур MoveTo (x1, y1) и LineTo (x2, y2) .
Процедуры работают в паре: MoveTo передвигает курсор в определенную точку, а процедура LineTo рисует линию с этой точки до точки, определенной параметром данной процедуры.

uses GraphABC; begin . SetPenColor(clblue); MoveTo (x1, y1); LineTo (x2, y2); LineTo (x3, y3); LineTo (x4, y4); LineTo (x5, y5); end.

Задание 0: При помощи операторов SetPenColor(), LineTo (x2, y2) и MoveTo (x1, y1) нарисовать квадрат и равносторонний треугольник.

[Название файла: L4_2task0.pas ]

Для установки размеров графического окна используется процедура

Рисование фигур

uses GraphABC; begin Rectangle(50,50,200,200); end.

uses GraphABC; begin Rectangle(50,50,200,200); FloodFill(100,100,clBlue); end.

Line(x1,y1,x2,y2);
LineTo(x,y);

uses GraphABC; begin setpenwidth(20); setpencolor(clred); moveTo(300,100); lineTo(500,300); lineto(100,300); lineto(300,100); floodfill(300,200,clgreen); end.

uses GraphABC; begin Circle(500,200,100); FloodFill(500,200,clred); end.

uses GraphABC; Begin SetPenWidth(10); Arc(300,250,150,45,135); end.

[Название файла: L4_2task1.pas ]

[Название файла: L4_2task2.pas ]

Функция random для использования окраски

Задание 3: Нарисовать горизонтальный ряд окружностей радиусом 10 на расстоянии 100 от верхнего края экрана и с такими горизонтальными координатами 50, 80, 110, 140, … , 290.

* раскрасить круги случайным цветом

[Название файла: L4_2task3.pas ]

[Название файла: L4_2task4.pas ]

Задание 5:
Воспроизвести изображение при помощи программы:

[Название файла: L4_2task5.pas ]

Нарисовать штриховку на Паскале можно, используя процедуры рисования прямоугольника и линии:

Программа будет выглядеть следующим образом:

uses graphABC; var i, x1, x2, y1, y2, N: integer; h, x: real; begin x1 := 100; y1 := 100; x2 := 300; y2 := 200; N := 10; Rectangle (x1, y1, x2, y2); h := (x2 - x1) / (N + 1); x := x1 + h; for i:=1 to N do begin Line(round(x), y1, round(x), y2); x := x + h; end; end.

[Название файла: L4_2task6.pas ]

Анимация в Паскале

Анимация в программировании заключается в том, что сначала рисуется фигура цветным инструментом, затем с тем же координатами рисуется та же фигура белым цветом. После чего происходит сдвиг фигуры и действия повторяются.

uses GraphABC; var x:integer; begin x:=40; repeat SetPenColor(clWhite); Circle(x,100,10); SetPenColor(clBlack); Circle(x,100,10); x:=x+1 until x>600; end.

Задание 7: Выполнить анимацию движения квадрата по следующей траектории:

Вычислим х и y для эллипса из уравнения в параметрической форме: x=a*cos(t) и y=b*sin(t), где а и b - большая и малая полуось. При а=b получим окружность. Зададим угол от 0 до 2*ПИ() в 20 (21) точках.

Выберем тип диаграммы Точечная с гладкими кривыми и маркерами.

Т.к. MS EXCEL автоматически подбирает масштаб координатных осей, то для того чтобы форма эллипса и окружности соответствовала заданной, необходимо зафиксировать максимальное, минимальное значение и цену деления оси.

СОВЕТ : Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .

Из многочисленных построений здесь рассматрива­ются только те, которые часто встречаются при вы­полнении чертежей.

Деление отрезка прямой на две и четыре равные части выполняется в следующей последовательности.

Из концов отрезка А В циркулем проводят две дуги окружности радиусом R, несколько большим поло­вины данного отрезка, до взаимного пересечения в точках n и m (рис. 43, а). Точки тип соединяют пря­мой, которая пересекает отрезок АВ в точке С. Точка С делит отрезок А В на две равные части. Проделав подобное построение для отрезка АС, находим его середину — точку D. Повторив построение для отрезка СВ, разделим отрезок на четыре равные части.

При вычерчивании детали, показанной на рис. 43, б, применяется способ деления отрезка на четыре части.

Деление отрезка прямой на любое число равных частей. Пусть отрезок А В требуется разделить на И равных частей. Для этого из любого конца данного отрезка, например из точки В (рис. 44, проводят под произвольным острым углом вспомогательную прямую линию ВС, на которой от точки В измеритель­ным циркулем откладывают 11 равных отрезков произвольной величины. Крайнюю точку 11 последней отложенной части соединяют с точкой А прямой Затем с помощью линейки и угольника проводят ряд прямых, параллельных прямой которые и разделяют отрезок А В на 11 равных частей.

На рис. 44, б показана деталь, при изготовлении которой необходимо разместить 10 центров отверстий; отверстия равномерно расположены на длине L. В этом случае применяется описанный выше способ деления отрезка прямой на равные части.

ПОСТРОЕНИЕ И ИЗМЕРЕНИЕ УГЛОВ ТРАНСПОРТИРОМ

Транспортир — это прибор для измерения и построе­ния углов. Это полукруг с разбивкой на градусы, сое­диненный с опорной планкой.

Для измерения угла транспортир прикладывают опорной планкой к одной из сторон данного угла (рис. 45, а) так, чтобы вершина угла (точка А) совпадала с точкой О на транспортире. Величину угла САВ в гра­дусах определяют по шкале транспортира.

Для построения угла заданной величины (в градусах) со стороной А В и вершиной в точке к приклады­вают транспортир так, чтобы его центр (точка О) сов­пал с точкой А прямой АВ, затем у деления шкалы транспортира, соответствующего заданному числу градусов (например, 55°), наносят точку n. Транспортир убирают и проводят через точку n отрезок АС — полу­чают заданный угол САВ (рис. 45, б).

Углы можно строить при помощи угольников с углами 45, 30 и 60° и линейки или рейсшины. На рис. 46 показано, как при различных положениях угольников на рейсшине можно строить углы 60 (120), 30 (150), 45° (135°) и другие при использовании одновременно двух угольников..

ПОСТРОЕНИЕ И ДЕЛЕНИЕ УГЛОВ

Деление угла на две и четыре равные части. Из вер­шины угла провести произвольным радиусом дугу до пересечения со сторонами угла в точках (рис. 47, а). Из полученных точек проводят две дуги радиусом R, несколько большим половины длины дуги n и к, до взаимного пересечения в точке m. Вершину угла соединяют с точкой т прямой, которая делит угол ВАС пополам. Эта прямая называется биссектрисой угла ВАС. Повторяя это построение с полученными углами В Ат и nАС угол ВАС можно разделить на четыре равные части и т. д.

Деление прямого угла на три равные части. Из вер­шины А прямого угла (рис. 47, б) произвольным ради­усом R описывают дугу окружности до пересечения ее со сторонами прямого угла в точках a и b из которых проводят дуги окружности того же радиуса R до пересечения с дугой ab в точках m и n. Точки m и n соединяют с вершиной угла А прямыми и получают стороны Аm и Аn углов В Аm и nА С,равных 1/3 прямого угла, т. е. 30°. Если каждый из этих углов разделить пополам, то пря­мой угол будет разделен на шесть равных частей, ка­ждый из углов будет равняться 15°. Прямой угол АВС можно разделить на три равные части угольником с углами 30 и 60° (рис. 48, а). При выполнении чертежей нередко требуется разделить прямой угол на две рав­ные части. Это можно выполнять угольником с углом 45° (рис. 48, б).

Построение угла, равного данному. Пусть задан угол ВАС. Требуется построить такой же угол. Через произвольную точку А₁ проводим прямую А₁С₁. Из точки А описываем дугу произвольным радиусом R, которая пересечет угол ВАС в точках (рис. 49,а). Из точки A ₁ проводим дугу тем же радиусом и полу­чаем точку m₁. Из точки A₁ проводим дугу радиусом R₁ равным отрезку mn, до пересечения с ранее прове­денной дугой радиуса R в точке n₁ (рис. 49, б). Точку n₁ соединяем с точкой А₁ и получаем угол B₁A₁C₁ вели­чина которого равна заданному углу ВАС.

Применение вышеизложенного построения угла по заданному показано на рис. 49, в и г. На рис. 49, в изоб­ражена деталь, чертеж которой надо вычертить, а на рис. 49, г показан этот чертеж, при выполнении кото­рого использован способ построения угла по заданно­му.

СПОСОБЫ ПОСТРОЕНИЯ МНОГОУГОЛЬНИКОВ

Способ триангуляции. Построение многоугольников этим способом основано на последовательном построе­нии ряда треугольников, примыкающих сторонами друг к другу. Этот способ будет применяться в дальней­шем при построении разверток поверхностей геоме­трических тел.

Рассмотрим пример такого построения. На рис. 50, а показана пластина с пятиугольным отверстием. Изме­ряя длины сторон пятиугольника, можно построить на чертеже контурное очертание многоугольного отвер­стия.

Треугольники в рассматриваемом многоугольнике можно получить, проведя диагонали 14 (рис. 50, а). Последовательность построения многоугольника на чертеже в данном примере следующая.

На детали произвольно выбираем базовую линию (например, А В), на которую из точек 7 и 2 опускаем перпендикуляр, и получаем точки E и G. На чертеже наносим базовую линию A₁B₁ на которой откладываем отрезок E₁G₁ равный отрезку EG. Из точек и G, восставляем перпендикуляры, на которых отклады­ваем взятые с детали отрезки и G1 (рис. 50, б). Получим точки 1₁и2₁. Из точек как из центров, циркулем описываем две дуги радиусами, равными отрезками 13 и 23, взятых с детали. Точка пересечения дуг является вершиной 3₁ искомого треугольника 1₁2₁3₁. Таким же способом из точек 7₁ и 3₁ описываем две дуги радиусами, равными отрезкам 34 и 14, нахо­дим вершину 4₁. Затем из точек 4₁ и 1₁, как из центров, описываем две дуги радиусами, равными отрезкам 45 и 15, определяем последнюю вершину пятиугольника 5₁(рис. 50, б).

ОПРЕДЕЛЕНИЕ ЦЕНТРА ДУГИ ОКРУЖНОСТИ

Многие детали машин и приборов имеют контур очертания, состоящий из прямых линий, лекальных кривых и дуг окружностей. При вычерчивании деталей часто приходится определять величину радиусов дуг окружностей контурных очертаний детали и находить положение центров этих дуг. На рис. 51, а показана деталь (кронштейн), левая часть ребра которой выполнена по дуге окружности.

Чтобы найти положение центра и величину радиуса данной дуги, предварительно делают отпечаток дуги на бумаге. При помощи циркуля и линейки можно определить центр и размер радиуса дуги окружности, для этого на отпечатке дуги намечают три произ­вольно расположенные на ней точки А, В и С (рис. 51, б) и проводят хорды АВ и ВС. При помощи циркуля и линейки проводят перпендикуляры через середины хорд А В и ВС. Точка пересечения перпендикуляров

(точка О) является искомым центром дуги детали, а расстояние от точки О до любой точки дуги будет раз­мером радиуса.

ДЕЛЕНИЕ ОКРУЖНОСТИ НА РАВНЫЕ ЧАСТИ

Некоторые детали машин и приборов имеют эле­менты, равномерно расположенные по окружности, например, детали на рис. 52—59. При выполнении чер­тежей подобных деталей необходимо знать правила деления окружности на равное количество частей.

Деление окружности на четыре и восемь равных частей. На рис. 52, а показана крышка, в которой име­ется восемь отверстий, равномерно расположенных по окружности. При построении чертежа контура крышки (рис. 52 г) необходимо разделить окружность на восемь равных частей. Это можно сделать с помощью угольника с углами 45° (рис. 52, в), гипоте­нуза угольника должна проходить через центр окруж­ности, или построением.

Два взаимно перпендикулярных диаметра окружно­сти делят ее на четыре равные части (точки 7, 3, 5, 7 на рис. 52, б). Чтобы разделить окружность на восемь равных частей, применяют известный прием деления прямого угла с помощью циркуля на две равные части. Получают точки 2, 4, 6, 8.

Деление окружности на три, шесть и двенадцать рав­ных частей. Во фланце (рис. 53, а) имеется три отвер­стия, равномерно расположенных по окружности. При выполнении чертежа контура фланца (рис. 53, г) нужно разделить окружность на три равные части.

Для нахождения точек, делящих окружность радиуса R на три равные части, достаточно из любой точки окружности, например точки А, провести дугу ради­усом R. Пересечения дуги с окружностью дают две искомые точки 2 и 3; третья точка деления будет нахо­диться на пересечении оси окружности, проведенной из точки Л, с окружностью (рис. 53, б).

Разделить окружность на три равные части можно также угольником с углами 30 и 60° (рис. 53, в), гипотенуза угольника должна проходить через центр окруж­ности.

На рис. 54, б показано деление окружности цирку­лем на шесть равных частей. В этом случае выполня­ется то же построение, что на рис. 53, б но дугу описы­вают не один, а два раза, из точек и радиусом R , равным радиусу окружности.

Разделить окружность на шесть равных частей можно и угольником с углами 30 и 60° (рис. 54, в). На рис. 54, а показана крышка, при выполнении чертежа которой необходимо выполнить деление окружности на шесть частей.

Чтобы выполнить чертеж детали (рис. 55, а), кото­рая имеет 12 отверстий, равномерно расположенных по окружностям, нужно разделить осевую окружность на 12 равных частей (рис. 55, г).

При делении окружности на 12 равных частей с помощью циркуля можно использовать тот же прием, что и при делении окружности на шесть равных частей (рис. 54, б),но дуги радиусом R описывать четыре раза из точек 1, 7, 4и 10 (рис. 55, б).

Используя угольник с углами 30 и 60° с последующим поворотом его на 180°, делят окружность на 12 равных частей (рис. 55, в).

Деление окружности на пять, десять и семь равных частей. В плашке (рис. 56, а) имеется пять отверстий, равномерно расположенных по окружности. Выпол­няя чертеж плашки (рис. 56, в), необходимо разделить окружность на пять равных частей. Через намеченный центр О (рис. 56, б)

при помощи рейсшины и уголь­ника проводят осевые линии и из точки О циркулем описывают окружность заданного диаметра. Из точки А радиусом R, равным радиусу данной окружности, проводят дугу, которая пересечет окружность в точке n. Из точки n опускают перпендикуляр на горизон­тальную осевую линию, получают точку С. Из точки С радиусом R₁ равным расстоянию от точки С до точки 1, проводят дугу, которая пересечет горизонтальную осевую линию в точке т. Из точки 1 радиусом R , рав­ным расстоянию от точки 1 до точки m, проводят дугу, пересекающую окружность в точке 2. Дуга 12 является 1/5 длины окружности. Точки 3,4 и 5 находят, отклады­вая циркулем отрезки, равные m1.

На рис. 58, а изображен шкив, а на рис. 58, в — чер­теж шкива, где окружность разделена на семь равных частей.

Деление окружности на семь равных частей пока­зано на рис. 58, б. Из точки А проводится вспомога­тельная дуга радиусом R, равным радиусу данной окружности, которая пересечет окружность в точке . Из точки n опускают перпендикуляр на горизонталь­ную осевую линию. Из точки 1 радиусом, равным отрезку nс, делают по окружности семь засечек и полу­чают семь искомых точек.

Деление окружности на любое число равных частей. С достаточной точностью можно делить окружность на любое число равных частей, пользуясь таблицей коэффициентов для подсчета длины хорды (табл. 9).

Зная, на какое число (n) следует разделить окруж­ность, находят по таблице коэффициент . При умно­жении коэффициента k на диаметр окружности D получают длину хорды l, которую циркулем отклады­вают на окружности n раз.

При построении чертежа кольца (рис. 59, а) необхо­димо окружность диаметра D=142 мм разделить на 32 равные части. Количеству частей окружности n=32 соответствует коэффициент k=0,098. Подсчитав длину хорды l=Dk=142x0,098= 13,9 мм, ее циркулем откла­дывают на окружности 32 раза (рис. 59, б и в).

Читайте также:

  
• Как сделать сеть на бобра
  
• Как сделать курицу в утятнице
  
• Как сделать спортивный стенд
  
• Как сделать инфографику в excel
  
• Как сделать кнопку сохранить в делфи