Как построить 90 доверительный интервал в r studio
Для изучения и экспериментов лучше подходит интерактивный режим. Поэтому будем использовать именно его.
На примере этих (и других) данных будет рассмотрены возможности языка:
X = " 181.1 167.9 170.5 194.1 171.6 168.6 180.7 184.9 165.3 165.5 171.1 174.4 175.2 180.3 181.2 168.9 176.2 167.4 165.9 177.2 180.8 173.9 163.5 175.0 171.0 177.6 173.6 185.8 184.0 178.7 174.3 170.3 178.6 172.3 162.3 166.3 160.4 163.0 174.7 183.1 "
Y = " 163.3 172.6 154.3 159.8 174.0 159.0 180.1 168.9 177.0 166.4 162.7 169.3 170.3 161.8 171.9 177.3 166.8 175.5 175.1 174.8 161.0 169.8 177.9 174.3 168.7 176.6 156.3 179.3 178.3 168.7 178.5 151.0 164.0 159.5 180.9 178.7 166.0 169.5 167.0 150.4 "
Данные представлены не столбцом, а строкой. Поэтому для начала разобъём её на подстроки, а потом преобразуем в вещественные числа:
Загрузка данных
Текстовые файлы. Загрузить текстовый файл как список строк';' - разделитель полей;
header - есть ли заголовок.
Работа с данными
N X Y
Min. : 0.00 Min. : 6.26 Min. : 3.74
1st Qu.:24.75 1st Qu.:10.54 1st Qu.: 9.33
Median :49.50 Median :12.27 Median :11.14
Mean :49.50 Mean :12.34 Mean :10.91
3rd Qu.:74.25 3rd Qu.:14.12 3rd Qu.:12.55
Max. :99.00 Max. :20.65 Max. :17.94
Работа с DataFrame
names(D) - имена полей
nrow(D), ncol(D) - число строк, столбцов
Доступ к полям. Имя поля (столбца) записывается после знака $:
Доступ к даныым можно получить используя индексацию: строка, столбец.
D[42,] - 42 строчка таблицы
D[,2] - данные из второго столбца
Указывать набор конкретных строк\столбцов можно вектором:
D[ c(1,3,7, 13), ]
исключить эти столбцы:
D[ , - c(1,2) ]
Вместо индексов столбцов можно указывать их имена (тут унарный минус не работает):
mtcars[ , c('wt', 'am')]
Создание нового поля (заполненного нулями)
Загрузка из Интернета.
.
Среда
Самая популярная среда - R Studio.

Числовые характеристики
Графики
Дополнительные параметры функции plot:
xlab = "Ось X", ylab = "Ось Y" - подписи к осям;
col = "red" - цвет маркеров;
type = "b" - тип графика ( p - точки (по умолчанию), l - линии, b - линии и точки, и т.п. см. справку по plot);
main = "Заголовок" - подпись сверху;
sub = "Подзаголовок" - подпись снизу.
Добавим координатную сетку:

ggplot2
Более эстетичные графики можно построить с помощью библиотеки ggplot2

aes(x=D$X, y=D$Y) - задаёт соответствие осей данным
geom_point() - определяет способ отображения данных
Эта статья — продолжение первой части. В этой серии статей я рассматриваю применение набирающего популярность языка программирования R для решения распространенных статистических задач.
В данной и следующей статье я показываю как выбрать для обработки качественных и количественных данных правильные тесты и реализовать их в R. Данные методы позволяют получить реальное представление об объекте, процессе или явлении по какому-либо параметру, т.е. позволяют сказать «хорошо» или «плохо». Они не потребуют глубоких знаний программирования и статистики, и пригодятся людям различного рода деятельности.
Перед тем как начать, сделаю важное замечание. Самое сложное, выбрать, как анализировать данные. R — это инструмент, он сделает все, что вы ему скажете. Но если вы примените не тот метод, ваши результаты не будут иметь смысла.
Немного теории
Тестирование применяется для того, чтобы сравнить две случайные величины, т.е. доказать наличие или отсутствие разницы между ними. Основная идея в том, что происходит сопоставление разницы средних значений и стандартного отклонения.
В статистике оперируют так называемыми гитпотезами. Их всего две. Основная, H0, что отличия нет:
Альтернативная, H1, отличие величин:
Гипотеза может быть и вида x1<x2, и тогда вам придется использовать односторонние тесты. Но на практике это делается крайне редко.
Также необходимо задать ошибку первого рода, α. Я упоминал ее в прошлой статье, как (1 — чувствительность) для биноминальной классификации. Это ошибка, с которой мы предсказываем H1. Стандартной α являетя 5%.

Каждый тест на выходе дает 2 значения: тест-статистику и p-значение, что по сути одно и тоже. Кратко объясню что это. Как мы знаем, доверительный интервал (т.е. интервал, в котором случайная величина находится с заданой вероятностью), который мы будет составлять для H0, представляется формулой:
где x — среднее значение, σ — стандартное отклонение.
ζ — это квантиль используемого распределения, т.е. множитель, который соответствует интервалу заданной вероятности. α — ошибка первого рода, т.е. вероятность, что x окажется за пределами интервала.
В тесте имеется значение x альтернативной гипотезы. Тест-статистика характеризует его в размерности квантиля, а p-значение в размерности вероятности. Если p-значение меньше, чем α, либо тест-статистика больше квантиля, то альтернативная гипотеза находится за пределами этого интервала. В этом случае, c вероятностью ошибки alpha, мы принимаем H1, т.к. считаем, что тестируемое значение не может относиться к H0. Тест-статистика и p-значение являются результатами теста.
Если мы построим доверительный интервал, то получим по сути тоже самое. Возможно, многим это будет естественнее. Тем не менее, тесты устроены по принципу p-значения, давайте ими пользоваться и не задумываться на концептуальном уровне (тем более люди этим всю жизнь занимались, видимо, нужно именно так).
Выбор методики

Данные являются парными, если оба значения получены с одного объекта. Например, сравнение результатов “до и после” или использование двух алгоритмов на одних данных. Однозначно, что парный тест менее строгий, т.е. эффект можно доказать при меньшей выборке.
Этапы работы с данными
Вы определили с чем имеете дело. Что делать дальше. Вот некоторый алгоритм работы.
- Описание. Получить средние значения, среднеквадратичные отклонения, пострить графики распределения
- Принятие решения
- Соответствующий тест
- Получение доверительного интервала (в R включено в тесты)
Обработка качественных данных
Качественные данные это “да” и “нет”. Примеры применения: сравнение работы двух методик/алгоритмов/отделов компаний, нахожение влияния наличия антивируса на заражение компьютера/курения на рак легих/текста рекламы на факт продажи. Для этих данных работает биноминальное распределение.
Для примера я взял несколько абстрактные бинарные данные, две группы по 25 элементов. Каждый элемент это 0 или 1. Будем работать с ними, как я указал выше: сперва красиво представим эти данные (возможно после этого никакие тесты будут не нужны), затем будем проводить анализ.
Для примера, построим биноминальное распределение для первой выборки, полагая, что значение вероятности является истинным. Таким образом, мы получим, как на основании имеющихся данных должна себя вести случайная величина.
![]()
Если нам интересна вероятность:
![]()
![]()
Для описания данных нужно предстивить среднюю веоятность с доверительным интервалом для каждой группы. Функция плотности вероятности выглядит следующим образом:
В R нам поможет билиотека binom. Установив ее, используем код:
![]()
Уже сейчас можно сделать вывод, что хотя разница средних значений существенна, доверительные интервалы пересекаются, что в целом было ожидаемо для таких маленьких выборок. Также отмечу, что если бы вы считали по выше приведенной формуле, то получили другие результаты. В данном расчете используется точный метод, в то время как формула являтся приближенной. Разница уменьшается с увеличением выборки.
Хи-квадрат тест используется для анализа нескольких биноминальных выборок. Он распространен, т.к. его легко провести руками.
![]()
Нам выдали предупреждение. Дело в том, что хи-квадрат тест является приближенным (хотя даже тут R использует дополнительную коррекцию, ее можно отключить, если нужно). Для маленьких выборок он дает ошибку. Существует более сложный, но абсолютно точный тест, учитывающий неизвестность некоторых параметров, неучтенную в хи-квадрат тесте. Это тест Фишера.
![]()
P-значение 9.915%, что больше, чем 5%. Поэтому оставляем гипотезу H0 — разницы между величинами нет.
Для этих тестов можно брать несколько групп. В этом случае H1 будет отражать отличие хотя бы одной группы от других.
Итоги
На этом я завершаю эту статью. Сегодня я рассказал о том, как использовать тесты, как выбрать подходящий тест, а также подробно разобрал анализ качественных данных, применение хи-квадрат теста и теста Фишера. Текста было больше, чем R, но никуда не деться. В следующей, я перейду к анализу количественных выборок.
Стандартные ошибки и доверительные интервалы параметров модели, рассчитанные в соответствии с Центральной Предельной ТеоремойКак видно из представленных результатов, постоянная Хаббла была оценена ( Estimate ) в 76.581 км/с на мегапарсек. Стандартная ошибка ( Std. Error ) этого значения составила 3.965 км/с на мегапарсек. Другими словами, мы можем сказать, что истинное значение постоянной Хаббла принадлежит нормально распределенной совокупности, математическое ожидание и стандартное отклонение которой составляют около 76.581 и 3.965 км/с на мегапарсек соответственно. Заметьте, однако, следующее обстоятельство: хотя наиболее вероятное истинное значение постоянной Хаббла составляет около 77 км/с на мегапарсек (после округления значения 76.581), возможны также и другие значения. Чтобы охарактеризовать эту неопределенность, мы можем рассчитать доверительный интервал - непротиворечащий имеющимся данным диапазон значений, в котором истинное значение постоянной Хаббла находится с определенной вероятностью (например, 95%).
Поскольку, как уже было отмечено выше, выборочная оценка постоянной Хаббла в лимите имеет нормальное распределение, мы могли бы рассчитать 95%-ный доверительный интервал, вспомнив, что примерно 95% всех значений нормального распределения лежат в диапазоне +/- 2 стандартных отклонения относительно среднего значения. Для нашего примера получаем: \(76.581 - 2 \times 3.965 = 68.651\) и \(76.581 + 2 \times 3.965 = 84.511\) км/с на мегапарсек. Однако неопределенность имеется в отношении не только оценки постоянной Хаббла, но и оценки стандартного отклонения соответствующего нормального распределения. Не углубляясь в детали, отметим, что в связи с эти обстоятельством более точные значения границ доверительного интервала дадут вычисления, основанные на свойствах не нормального, а t-распределения Стьюдента. Так, границы 95%-го доверительного интервала для параметра \(\beta\) составят:
где \(t_\) - 0.975-квантиль t-распределения с \(n - p\) числом степеней свободы (где \(n\) - объем выборки, а \(p\) - число параметров модели), \(SE_\) - стандартная ошибка параметра \(\beta\).
Используя эти оценки нижней и верхней границ 95%-ного доверительного интервала, мы можем рассчитать диапазон значений, в котором с вероятностью 95% находится истинный возраст Вселенной:
Заметьте, что полученный таким способом доверительный интервал включает значение возраста Вселенной, рассчитанное на основе самых последних космологических данных (13.798 млрд. лет).Стандартные ошибки и доверительные интервалы параметров модели, рассчитанные бутстреп-методом
Насколько мне известно, устоявшегося перевода термина "bootstrap" с английского языка на русский не существует. Используются разные варианты: "бутстреп", "бутстрэп", "бутстрап", "размножение выборок", "метод псевдовыборок" и даже "ресамплинг" (от англ. "resampling"). Несмотря на сложности с русскоязычным названием, суть метода, тем менее, весьма проста (подробнее см. оригинальную работу Efron 1979). Предположим, что у нас есть выборка некоторого ограниченного объема и мы имеем основания полагать, что эта выборка является репрезентативной (т.е. хорошо отражает свойства генеральной совокупности, из которой она была взята). Идея бутстреп-метода заключается в том, что мы можем рассматривать саму эту выборку в качестве "генеральной совокупности" и, соответственно, можем извлечь большое число случайных выборок из этой исходной совокупности для расчета интересующего нас параметра (или параметров). Очевидно, что благодаря случайному формированию этих новых выборок, будет наблюдаться определенная вариация значений оцениваемого параметра. Другими словами, мы получим некоторое распределение значений этого параметра. Рассчитав стандартное отклонение этого распределения, мы получим оценку стандартной ошибки параметра, которая при большом числе наблюдений будет асимптотически приближаться к истинной стандартной ошибке. Аналогично, найдя, например, 0.025- и 0.975-квантили этого распределения, мы получим оценки нижней и верхней границ 95%-ного доверительного интервала.
Применим бутстреп-метод для оценки стандартной ошибки и 95%-ного доверительного интервала для постоянной Хаббла из рассмотренной выше задачи. На рисунке ниже приведены примеры 6 случайных выборок объемом 24 наблюдения каждая, извлеченных из исходной совокупности данных. Эти выборки формируются "с возвратом" - это значит, что однажды попав в новую выборку, то или иное наблюдение "возвращают" в исходную совокупность и оно может быть выбрано снова (следовательно, определенные наблюдения могут повторяться в новой выборке несколько раз).
![]()
Обратите внимание: на представленном рисунке общий тренд сохраняется ("чем больше x, тем больше y"), однако входящие в состав каждой выборки (A - F) наблюдения несколько различаются, что в итоге приведет и к несколько различающимся оценкам постоянной Хаббла при подгонке линейной модели при помощи функции lm() .
- data : таблица с исходными данными;
- statistic : функция, выполняющая вычисление интересующего нас параметра(-ов);
- R : число повторных выборок, по которым рассчитывается этот параметр.
Теперь подадим regr() на функцию boot() :
При выводе содержимого объекта results на экран получим:
В представленных результатах original - это значение постоянной Хаббла, оцененное по исходным данным (см. выше); bias (смещение) - разница между средним значением 1000 бутстреп-оценок постоянной Хаббла и исходной оценкой; std. error - бутстреп-оценка стандартной ошибки постоянной Хаббла. Обратите внимание на то, что полученная бутстреп-оценка стандартной ошибки выше, чем рассчитанная по исходным данным.
Для объектов класса boot (к которому принадлежит results ) имеется метод plot , который позволит изобразить графически полученное распределение бутстреп-оценок постоянной Хаббла и одновременно проверить нормальность их распределения при помощи графика квантилей.
![]()
Как отмечено выше, мы можем оценить нижнюю и верхнюю границы 95%-ного доверительного интервала постоянной Хаббла, найдя 0.025- и 0.975-квантили изображенного выше распределения:
Используя эти значения, рассчитаем соответствующие границы значений возраста Вселенной:
Следует отметить, что рассчитанные таким образом границы доверительного интервала могут оказаться смещенными. В состав пакета boot входит функция boot.ci() , которая позволяет рассчитать несколько других типов доверительных интервалов, включая интервалы с поправкой на смещение (аргумент type = "bca" ; подробнее см. ?boot.ci ):
Подробнее о реализации бутстреп-регрессии средствами R можно прочитать в работе Fox (2012).
Стандартные ошибки и доверительные интервалы параметров модели, рассчитанные путем симуляций
- Подгонка определенной модели к имеющимся данным;
- Использование полученных оценок параметров модели для симуляции большого количества альтернативных, но в то же время правдоподобных (т.е. непротиворечащих данным) реализаций этих параметров.
- При помощи обычного регрессионного анализа оцениваются вектор регрессионных коэффициентов \(\hat\), ковариационная матрица \(V_<\hat>\) и стандартное отклонение остатков \(\hat\).
- Создается большое число реализаций вектора \(\beta\) и стандартного отклонения остатков \(\sigma\). Для каждой реализации:
- симулируется значение \(\sigma = \hat\sqrt\), где \(X\) - это значение статистики хи-квадрат, случайным образом извлеченное из соответствующего распределения с \(n-k\) степенями свободы.
- с учетом полученного значения \(\sigma\), симулируется вектор \(\beta\) путем случайного извлечения значений из многомерного нормального распределения со средним значением \(\hat\) и ковариационной матрицей \(V_<\hat>\).
![]()
На представленном выше рисунке изображено распределение 1000 симулированных значений постоянной Хаббла. Мы можем оценить стандартную ошибку постоянной Хаббла, рассчитав стандартное отклонение этого распределения:
Как видим, эта стандартная ошибка (как и в случае с бутстреп-анализом) также оказалась выше исходной оценки (см. summary(M) ).
Я работаю над проблемой, основанной на наборе данных, который включает копировальный бизнес, предоставляющий сервисные вызовы для своих клиентов. Набор данных-это набор из 45 экземпляров, который описывает количество минут, затраченных на вызов службы(v1), и количество копировальных аппаратов, имеющихся у клиента(v2).
Проблема заключается в следующем:
Оцените изменение среднего времени обслуживания при увеличении количества копировальных аппаратов на 1. Используйте 90-процентный доверительный интервал.
Я интерпретирую это как создание регрессионной функции для получения наклона, который примерно равен "изменению среднего времени обслуживания при увеличении числа копировальных аппаратов на 1". Однако я не знаю, как это сделать с доверительным интервалом 90%.
До сих пор функция регрессии генерируется примерно так:
Я получил следующее:
Запустив summary(), я получаю:
Доверительный интервал для b1 (наклон) равен:
b1 +/- t * (Стандартная ошибка)
Так это правильно?:
15.0352 +/- (.4831 * 31.123)
2 ответа
Привет, я новичок в R, и я надеялся, что кто-нибудь может дать мне несколько советов по построению регрессионной модели. У меня есть некоторые примеры данных, подобные приведенным ниже, которые содержат категориальные переменные, такие как переменная path. Я хотел бы преобразовать эти.
Пожалуйста, я хотел бы вычислить среднюю разницу с доверительным интервалом для двух переменных через другую категориальную переменную. Меня интересует вычисление доверительных интервалов для p1, p2 и pdiff Большое спасибо library(tidyverse) iris %>% mutate(out1 = Sepal.Length < 6, out2 =.
Вы правы, что доверительный интервал "Wald Type" будет рассчитан как b1 +/- t * (Стандартная ошибка). Однако "t" в этом уравнении является критическим значением t, а не значением t, указанным в сводке модели.
Вы можете посмотреть свое критическое значение t для 90% CI с 43 степенями свободы в R, например:
Так что тогда ваш CI будет be b1 +/- 1.68 * (Стандартная ошибка).
Вы можете дважды проверить это в R, используя функцию confint() .
После того как вы вычислите регрессию, вы получите оценку коэффициента со статистикой, такой как стандартная ошибка. Вы можете использовать их для расчета доверительного интервала для оценок.
Обновление:
Теперь, когда у нас есть некоторый код для просмотра, вы можете попробовать это:
Похожие вопросы:
Можно ли настроить выполнение задания apscheduler cron с интервалом в 90 секунд? (У меня есть 40 машин, которые я хотел бы запланировать равномерно в течение часа без жесткого кодирования информации.
Я ищу библиотеку javascript, способную рисовать гистограмму с доверительным интервалом. Вывод должен выглядеть так : турник линейные маркеры, указывающие нижний и верхний доверительные интервалы. В.
Привет, я новичок в R, и я надеялся, что кто-нибудь может дать мне несколько советов по построению регрессионной модели. У меня есть некоторые примеры данных, подобные приведенным ниже, которые.
Пожалуйста, я хотел бы вычислить среднюю разницу с доверительным интервалом для двух переменных через другую категориальную переменную. Меня интересует вычисление доверительных интервалов для p1, p2.
Я пытаюсь построить линейный график с гладким доверительным интервалом. Что-то похожее на это: В настоящее время я использую errorbars для отображения доверительного интервала. Итак,у меня есть 100.
Звучит очень сложно, но простой сюжет сделает его легким для понимания: у меня есть три кривые кумулятивной суммы некоторых значений с течением времени, которые являются синими линиями. Я хочу.
Я делаю линейный график и хотел бы построить среднее значение с доверительным интервалом в оттенках рядом с ним. Я могу построить данные так же, как линейный график, но это не очень хорошо работает.
Я работаю над созданием сводной таблицы с использованием пакета R gtsummary. Это на самом деле очень хорошо. Функция add_stat дает вам большую свободу для включения дополнений. Например, в моей.
Как видно, таблица отображает в разрезе каждого из 50 штатов США данные о:
- численности населения штата, по состоянию на 01.07.1975;
- доходах в 1974 г.;
- уровне грамотности, % от численности в 1970 г.;
- средней продолжительности жизни на основе данных 1969-71 гг.;
- уровне убийств (в расчете на 100 тыс. чел., 1976 г.);
- % людей, имеющих высшее образование в 1970 г.
- среднем количестве холодных дней (1931-1960);
- площади территории (кв. миль).
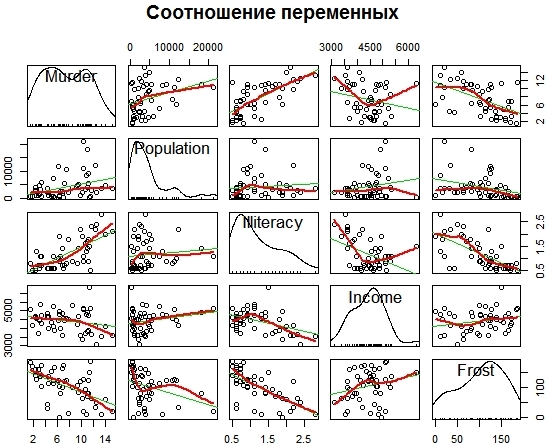
Сначала можно визуально представить, как соотносятся между собой переменные (рис. 3).
![Соотношение переменных]()
Рис. 3. Визуализация отношений между переменными
Чтобы увидеть зависимость уровня убийств по штатам (на примере США) от социально-экономических и прочих показателей, можно сократить количество графиков, учитывая только выборочные показатели – численность населения, грамотность, уровень доходов и количество холодных дней.
Для этого определим новую таблицу states1, а после построим графики зависимостей (рис. 4).
![Графики соотношений выбранных переменных]()
Рис. 4. Соотношение между выбранными переменными
Анализ
Корреляция
К тому же полезной является корреляционная матрица
Модель множественной регрессии
Разработаем модель линейной множественной регрессии на основе переменных, выбранных в таблице states1
Population + Illiteracy + Income + Frost, data = states1)
Доверительные интервалы
Найдем доверительные интервалы для параметров модели
Значимы только Illiteracy (уровень грамотности) и Population (численность населения)
Тест Дарбина-Утсона
lag Autocorrelation D-W Statistic p-value
1 -0.2006929 2.317691 0.268
Alternative hypothesis: rho != 0Тест показывает, что автокорреляция отсутствует.
Графики частичных остатков
Графики частичных остатков показывают связь между независимой переменной и зависимой (Murder) при условии, что остальные независимые переменные включены в модель (рис. 5). Для их построения воспользуемся записью
Читайте также:
- Как сделать резервную копию iphone в itunes на компьютере без пароля
- Что делать если в naruto shippuuden ultimate ninja storm revolution не хватает 512 кб памяти
- Где в скайпе посмотреть заблокированные контакты
- Psp что это за сокращение
- В чем состоит проблема выбора системы счисления для представления чисел в памяти компьютера