Чему равно самое большое число если под целое число выделяется ячейка памяти размером 16 бит
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 128×128 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Один пиксель кодируется 8 битами памяти, так как 2 8 = 256.
Тогда объем памяти, занимаемый изображением 2 14 * 8 = 2 17 бит = 2 14 байт = 2 4 Кбайт = 16 Кбайт.
Откуда там 8? Может быть 2 в 8 степени? И ответ тогда 512 Кб
На каждый пиксель 8 бит, всего 2 14 пикселей. Сколько бит на все пиксели? Правильно: .
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 128×128 пикселей при условии, что в изображении могут использоваться 128 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Один пиксель кодируется 7 битами памяти.
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 512x512 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Для того, чтобы закодировать один пиксель, то есть 256 цветов, требуется
Всего пикселей , то есть и памяти понадобится
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 1024x1024 пикселей при условии, что в изображении могут использоваться 16 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Для того, чтобы закодировать один пиксель, то есть 16 цветов, требуется
Всего пикселей , то есть и памяти понадобится
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 320×640 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Заметим, что 256 = 2 8 , то есть для хранения цвета одного пиксела изображения нужно использовать Значит, для хранения изображения размером 320×640 пикселей нужно использовать:

Что относится к основным правилам представления чисел в компьютере?
- Представление данных в компьютере имеет дискретную структуру
- Данные и программы в памяти компьютера хранятся в двоичном виде
- Представление информации посредством только двух состояний надёжно и помехоустойчиво
- Память компьютера не безгранична, и множество представимых в памяти компьютера величин ограничено и конечно
Вопрос 4
Какое число называют дополнительным кодом двоичного числа х в N-разрядной ячейке?
это новое число, дополняющее двоичное число до целого значения
это число, дополняющее двоичное число до значения 2 N -1
это число, дополняющее двоичное число до значения 2 N
Вопрос 5
Как выглядит внутреннее представление целого числа 248 в 2-байтовой ячейке?
- 0000000010111000
- 0000000011111001
- 1000000011111000
- 0000000011111000
Вопрос 6
Чему равно самое большое целое положительное число, если под целое число выделяется ячейка памяти размером в 16 бит?
11111111111111112 = 2 15 - 1 = 3276710
011111111111111112 = 2 15 - 1 = 3276710
1111111111111112 = 2 15 = 3276810
1111111111111112 = 2 15 - 1 = 3276710
Вопрос 7
Как выглядит число 1001010 в восьмиразрядном представлении?
- 001010
- 100001010
- 01001010
- 2001010
Вопрос 8
Как выглядит внутреннее представление числа -326 в 2-байтовой ячейке?
- 1000000010111011
- 0000000010111010
- 1000000010111010
Вопрос 9
Чему равно самое большое целое число, если под целое число выделяется ячейка памяти размером в 16 бит и формат представления чисел без знака?
Оперативная память компьютера состоит из ячеек, каждая из которых представляет собой физическую систему, состоящую из некоторого числа однородных элементов. Эти элементы обладают двумя устойчивыми состояниями, одно из которых соответствует нулю, а другое — единице. Каждый такой элемент служит для хранения одного из битов — разряда двоичного числа. Именно поэтому каждый элемент ячейки называют битом или разрядом (рис. 1.2).
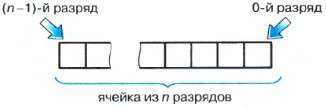
Рис. 1.2. Ячейка памяти
Для компьютерного представления целых чисел используется несколько различных способов, отличающихся друг от друга количеством разрядов (под целые числа обычно отводится 8, 16, 32 или 64 разряда) и наличием или отсутствием знакового разряда. Беззнаковое представление можно использовать только для неотрицательных целых чисел, отрицательные числа представляются только в знаковом виде.
Беззнаковое представление используется для таких объектов, как адреса ячеек, всевозможные счётчики (например, число символов в тексте), а также числа, обозначающие дату и время, размеры графических изображений в пикселях и т. д.
Максимальное значение целого неотрицательного числа достигается в случае, когда во всех разрядах ячейки хранятся единицы. Для n-разрядного представления оно будет равно 2 n -1. Минимальное число соответствует п нулям, хранящимся в n разрядах памяти, и равно нулю.
Ниже приведены максимальные значения для беззнаковых целых n-разрядных чисел:
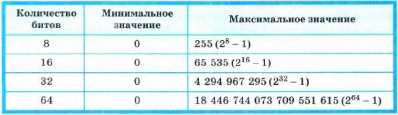
Для получения компьютерного представления беззнакового целого числа достаточно перевести число в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.
Пример 1. Число 5310 = 1101012 в восьмиразрядном представлении имеет вид:

Это же число 53 в шестнадцати разрядах будет записано следующим образом:

При представлении со знаком самый старший (левый) разряд отводится под знак числа, остальные разряды — под само число. Если число положительное, то в знаковый разряд помещается 0, если число отрицательное — 1. Такое представление чисел называется прямым кодом.
В компьютере прямые коды используются для хранения положительных чисел в запоминающих устройствах, для выполнения операций с положительными числами.
Презентация «Представление информации в компьютере» (Open Document Format)
Ссылки на ресурсы ЕК ЦОР
Федеральный центр информационных образовательных ресурсов:
Представление вещественных чисел
Любое вещественное число А может быть записано в экспоненциальной форме:
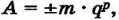
где:
m — мантисса числа;
q — основание системы счисления;
p — порядок числа.
Например, число 472 ООО ООО может быть представлено так: 4,72 • 10 8 , 47,2 • 10 7 , 472,0 • 10 6 и т. д.
С экспоненциальной формой записи чисел вы могли встречаться при выполнении вычислений с помощью калькулятора, когда в качестве ответа получали записи следующего вида: 4.72Е+8.
Здесь знак «Е» обозначает основание десятичной системы счисления и читается как «умножить на десять в степени».
Из приведённого выше примера видно, что положение запятой в записи числа может изменяться.
Для единообразия мантиссу обычно записывают как правильную дробь, имеющую после запятой цифру, отличную от нуля. В этом случае число 472 ООО ООО будет представлено как 0,472 • 10 9 .
Вещественное число может занимать в памяти компьютера 32 или 64 разряда. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.
Пример:

Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка числа, а точность определяется количеством разрядов, отведённых для хранения мантиссы.
Максимальное значение порядка числа для приведённого выше примера составляет 11111112 = 12710, и, следовательно, максимальное значение числа:
0,11111111111111111111111 • 10 1111111
Попытайтесь самостоятельно выяснить, каков десятичный эквивалент этой величины.
Широкий диапазон представления вещественных чисел важен для решения научных и инженерных задач. Вместе с тем следует понимать, что алгоритмы обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел.
САМОЕ ГЛАВНОЕ
Для компьютерного представления целых чисел используются несколько различных способов, отличающихся друг от друга количеством разрядов (8, 16, 32 или 64) и наличием или отсутствием знакового разряда.
Для представления беззнакового целого числа его следует перевести в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.
При представлении со знаком самый старший разряд отводится под знак числа, остальные разряды — под само число. Бели число положительное, то в знаковый разряд помещается 0, если число отрицательное, то 1. Положительные числа хранятся в компьютере в прямом коде, отрицательные — в дополнительном.
При хранении в компьютере вещественных чисел выделяются разряды на хранение знака порядка числа, самого порядка, знака мантиссы и мантиссы. При этом любое число записывается так:
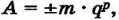
где:
m — мантисса числа;
q — основание системы счисления;
p — порядок числа.
Вопросы и задания
2. Как в памяти компьютера представляются целые положительные и отрицательные числа?
3. Любое целое число можно рассматривать как вещественное, но с нулевой дробной частью. Обоснуйте целесообразность наличия особых способов компьютерного представления целых чисел.
а) 01001100;
б) 00010101.
7. Запишите следующие числа в естественной форме:
а) 0,3800456 • 10 2 ;
б) 0,245 • 10 -3 ;
в) 1,256900Е+5;
г) 9,569120Е-3.
8. Запишите число 2010,010210 пятью различными способами в экспоненциальной форме.
9. Запишите следующие числа в экспоненциальной форме с нормализованной мантиссой — правильной дробью, имеющей после запятой цифру, отличную от нуля:
10. Изобразите схему, связывающую основные понятия, рассмотренные в данном параграфе.
Электронное приложение к уроку
Презентация «Представление информации в компьютере» (Open Document Format)
Ссылки на ресурсы ЕК ЦОР
Федеральный центр информационных образовательных ресурсов:

| Презентации, плакаты, текстовые файлы | Вернуться к материалам урока | Ресурсы ЭОР |


Cкачать материалы урока
Тебе известно, что компьютер работает только с двоичным кодом. \(0\) и \(1\) обозначают два устойчивых состояния: вкл/выкл, есть ток/нет тока и т. д. Оперативная память представляет собой контейнер, который состоит из ячеек. В каждой ячейке хранится одно из возможных состояний: \(0\) или \(1\). Одна ячейка — \(1\) бит информации или представляет собой разряд некоторого числа.
Целые числа в памяти компьютера хранятся в формате с фиксированной запятой . Такие числа могут храниться в \(8\), \(16\), \(32\), \(64\)-разрядном формате.
Для целых неотрицательных чисел в памяти компьютера выделяется \(8\) ячеек (бит) памяти.
Минимальное число для такого формата: \(00000000\). Максимальное: \(11111111\).
Переведём двоичный код в десятичную систему счисления и узнаем самое большое число, которое можно сохранить в восьмибитном формате.
1 × 2 7 + 1 × 2 6 + 1 × 2 5 + 1 × 2 4 + 1 × 2 3 + 1 × 2 2 + 1 × 2 1 + 1 × 2 0 = 255 10 .
Если целое неотрицательное число больше \(255\), то оно будет храниться в \(16\)-разрядном формате и занимать \(2\) байта памяти, то есть \(16\) бит.
Подумай! Какое самое большое число можно записать в \(16\)-разрядном формате?
Чем больше ячеек памяти отводится под хранение числа, тем больше диапазон значений.
В таблице указаны диапазоны значений для \(8\), \(16\) и \(32\)-разрядных форматов.

Для \(n\)-разрядного представления диапазон чисел можно вычислить следующим образом: от \(0\) до 2 n − 1 .
Запишем целое беззнаковое число \(65\) в восьмиразрядном представлении. Достаточно перевести это число в двоичный код.
Это же число можно записать и в \(16\)-разрядном формате.
![]()
Для целых чисел со знаком в памяти отводится \(2\) байта информации (\(16\) бит). Старший разряд отводится под знак: \(0\) — положительное число; \(1\) — отрицательное число. Такое представление числа называется прямым кодом.

Для хранения отрицательных чисел используют дополнительный и обратный коды, которые упрощают работу процессора. Но об этом ты узнаешь в старших классах.

Для хранения чисел в памяти компьютера используется два формата: целочисленный (естественная форма) и с плавающей точкой (нормализованная форма) (точка — разделительный знак для целой и дробной части числа).
Целочисленный формат (формат с фиксированной точкой) используется для представления в компьютере целых (англ. integer) положительных и отрицательных чисел. Для этого, как правило, используются форматы, кратные байту: 1, 2, 4 байта.
В форме с фиксированной запятой числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой (или точки), отделяющей целую часть от дробной.
Эта форма проста и привычна для большинства пользователей, но имеет небольшой диапазон представления чисел и поэтому не всегда пригодна при вычислениях. Если же в результате какой-либо арифметической операции получается число, выходящее за допустимый диапазон, то происходит переполнение разрядной сетки, и все дальнейшие вычисления теряют смысл.
Однобайтовое представление применяется только для положительных целых чисел. В этом формате отсутствует знаковый разряд. Наибольшее двоичное число, которое может быть записано при помощи 1 байта, равно 11111111, что в десятичной системе счисления соответствует числу 255(10).
Для положительных и отрицательных целых чисел обычно используется 2 и 4 байта, при этом старший бит выделяется под знак числа: 0 - плюс, 1 - минус.
Обрати внимание!
Если число вышло за указанные границы, произойдет переполнение! Поэтому при работе с большими целыми числами под них выделяется больше места, например 4 байта.
Формат с плавающей точкой (нормализованная форма) используется для представления в компьютере действительных чисел (англ. real). Числа с плавающей точкой размещаются, как правило, в 4 или 8 байтах.
Нормализованная форма представления чисел обеспечивает огромный диапазон их записи и является основной в современных ЭВМ.
Представление целого положительного числа в компьютере
Для представления целого положительного числа в компьютере используется следующее правило:
- число переводится в двоичную систему;
- результат дополняется нулями слева в пределах выбранного формата;
- последний разряд слева является знаковым, в положительном числе он равен 0.
Например, положительное число +13510 в зависимости от формата представления в компьютере будет иметь следующий вид:
- для формата в виде 1 байта - 10000111 (отсутствует знаковый разряд);
- для формата в виде 2 байтов - 0000000010000111;
- для формата в виде 4 байтов - 00000000000000000000000010000111.
Представление целого отрицательного числа в компьютере
Для представления целого отрицательного числа в компьютере используется дополнительный код. Такое представление позволяет заменить операцию вычитания числа операцией сложения с дополнительным кодом этого числа. Знаковый разряд целых отрицательных чисел всегда равен 1.
Для представления целого отрицательного числа в компьютере используется следующее правило:
- число без знака переводится в двоичную систему;
- результат дополняется нулями слева в пределах выбранного формата;
- полученное число переводится в обратный код (нули заменяются единицами, а единицы - нулями);
- к полученному коду прибавляется 1.
Обратный код для положительного двоичного числа совпадает с его прямым кодом, а для отрицательного числа нужно во всех разрядах, кроме знакового, нули заменить единицами и наоборот.
Дополнительный код для положительного числа совпадает с его прямым кодом, а для отрицательного числа образуется путем прибавления 1 к обратному коду.
Отрицательное число может быть представлено в виде 2 или 4 байт.
Представление вещественного (действительного) числа в компьютере
Вещественное число может быть представлено в экспоненциальном виде, например:
В этом формате вещественное число (R) представляется в виде произведения мантиссы (m) и основания системы счисления (P) в целой степени (n), называемой порядком.
Порядок n указывает, на какое количество позиций и в каком направлении должна сместиться в мантиссе точка (запятая), отделяющая дробную часть от целой. Мантисса, как правило, нормализуется, то есть представляется в виде правильной дроби 0 < m < 1.
Мантисса должна быть правильной дробью, у которой первая цифра после точки (запятой в обычной записи) отлична от нуля. Если это требование выполнено, то число называется нормализованным.
Для размещения вещественного числа обычно используется 2 или 4 байта.
В 2-байтовом формате представления вещественного числа первый байт и три разряда второго байта выделяются для размещения мантиссы, в остальных разрядах второго байта размещаются порядок числа, знаки числа и порядка.

В 4-байтовом формате представления вещественного числа первые три байта выделяются для размещения мантиссы, в четвертом байте размещаются порядок числа, знаки числа и порядка.

Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа.

Практические примеры
В числах одинарной точности:
на знак отводится 1 бит, на экспоненту - 8, на мантиссу - 23.
В нормализованных числах старший бит всегда равен единице и он не записывается в число, поэтому реально мантисса для таких чисел имеет размер 24 бита.
К экспоненте перед записью добавляется число 127.
Пример 1
Пример 2
Читайте также:


