Вычислить данные выражения при заданных числовых значениях аргументов excel
Формула задает правило для вычисления нового значения через исходные значения. Формула должна подчиняться определенным правилам записи, т.е. синтаксису. В Excel запись формулы всегда начинают со знака равенства. Часть формулы, следующая за знаком равенства, называется выражением.
Формулой в Excel называется последовательность, содержащая следующие элементы:
- знак равенства (=) – признак формулы в Excel;
- операнды (числа, текст, ссылки на ячейки, ссылки на массивы ячеек, встроенные функции);
- знаки операций (иногда их называют операторами);
- круглые скобки, причем число открывающих скобок должно быть равно числу закрывающих.
В первой работе уже приводились примеры вычисления по формулам, в которых выполнялись арифметические операции над числами. Числа в них задавались либо непосредственно в формуле, либо в виде ссылок на ячейки. Сейчас мы расширили это определение, включив в формулы функции в качестве операндов. Будем рассматривать только встроенные функции Excel.
Встроенные функции Excel
Встроенные функции Excel – это функции, вычисление которых выполняется по определенным алгоритмам, содержащимся в приложении Excel. Вызов встроенной функции происходит при вычислении по формуле, содержащей эту функцию. Запись функции в формуле Excel аналогична записи функций в математике. Она имеет вид , где f – имя функции, - аргументы. В общем случае аргументами функций могут быть данные любого вида, но для конкретной функции возможные аргументы определяются ее синтаксисом. Аргументы отделяются друг от друга точкой с запятой. Существуют встроенные функции, не содержащие аргументов, например, число p вычисляется с помощью функции ПИ(). Как видим, в этом случае после имени функции нужно ставить скобки, которые и являются признаком функции в записи. Встроенные функции Excel разбиты на категории. Каждая категория функций предназначена для определенных целей, например, имеются математические, логические, статистические функции и т.д. В данной лабораторной работе рассмотрим математические функции, причем только те, которые соответствуют элементарным функциям в математике. Они перечислены в табл. 2.1.
| Математическая функция | Встроенная функция Excel | Тип аргументов | Пояснение |
| |x| | ABS(x) | Любое число | Абсолютная величина x (модуль x) |
| arccos x | ACOS(x) | “ | Значение функции выражено в радианах |
| arcsin x | ASINx) | “ | Аналогично предыдущему |
| arctg x | ATAN(x) | “ | “ |
| cos x | COS(x) | “ | Косинус величины x, выраженной в радианах |
| EXP(x) | “ | Экспонента от x |
Продолжение таблицы 2.1
| ln x | LN(x) | “ | Натуральный логарифм x |
| logax | LOG(x;a) | “ | Логарифм x по основанию a |
| lg x | LOG10(x) | “ | Десятичный логарифм x |
| sin x | SIN(x) | “ | Синус величины x, выраженной в радианах |
| tg x | TAN(x) | “ | Тангенс величины x, выраженной в радианах |
| КОРЕНЬ(x) | “ | Квадратный корень | |
| p | ПИ() | Без аргумента | Число p |
| x a | СТЕПЕНЬ(x;a) | Любые числа | x в степени a |
Замечание. При наборе формул с клавиатуры безразлично, набираются строчные или прописные буквы, но нужно соблюдать соответствие языка имени функции. Ссылки на ячейки записываются только латинскими буквами. При указании типа аргумента не рассматриваются ограничения на область определения функций, но, разумеется, их нужно соблюдать.
Операции
Операции (арифметические и некоторые другие действия) в формулах записываются с помощью специальных символов, называемых знаками операций. Полный список операций Excel приведен в табл. 2.2.
| Знак операции | Операция | Пример записи |
| Арифметические операции | ||
| + | сложение | =А1+2 |
| - | вычитание | =4-С4 |
| * | умножение | =А3*С6 |
| / | деление | B3/5 |
| % | процент | =10% (равно 0,01) |
| ^ | возведение в степень | =2^3 (равно 8) |
Продолжение таблицы 2.2
| Операции сравнения | ||
| = | равно | A5=0 |
| < | меньше | A5<1 |
| > | больше | B3>100 |
| <= | меньше или равно | 3<=2*A10 |
| >= | больше или равно | A10>=0 |
| < > | не равно | A10< >5 |
| Операция связывания ячеек | ||
| : | Диапазон | =СУММ(А1:С10) |
| Текстовый оператор соединения | ||
| & | соединение текстов | =”Ответственный”&” Иванов И.П.” |
Операции выполняются над некоторыми данными (операндами). Операндом может быть число, ссылка на ячейку, ссылка на диапазон ячеек, функция, выражение, взятое в скобки. Рассмотрим формулы Excel:
1) =4-5,2+3,68 2) =2*5+12*6,2
Порядок действий в первой формуле следующий: вычитание, затем сложение. Во второй формуле сначала вычисляется 2*5, затем 12*6,2, после этого выполняется сложение ранее вычисленных чисел. Порядок выполнения операций определяется приоритетом операций. Для изменения порядка действий нужно использовать скобки.
Порядок вычисления значения по формуле Excel:
- вычисляются значения функций, входящих в формулу;
- вычисляются выражения в скобках;
- выполняются операции слева направо с учетом приоритета.
Приоритет арифметических операций в формулах Excel указан в табл. 2.3.
| Знак операции | Операция | Свойства | Приоритет |
| - | Изменение знака | Унарная | |
| ^ | Возведение в степень | Бинарная | |
| * , / | Умножение, деление | Бинарная | |
| + , - | Сложение, вычитание | Бинарная |
Комбинировать арифметические операции с прочими не рекомендуется (за исключением связывания массива).
Примеры
1. Порядок вычислений по формуле: =3+5*COS(B4)-2*A2:
2. Порядок вычислений по формуле =(3+A2^3/2)*3/5:
Замечания
1. При наборе сложной формулы легко сделать ошибку, поэтому надо хорошо знать синтаксис формул, чтобы в случае необходимости скорректировать формулу набором символов с клавиатуры.
2. Иногда Excel выводит подсказку пользователю, предлагая внести исправления в формулу. Их можно принять или отвергнуть после анализа предложения.
2. Порядок выполнения задания
Пример 1.Вычислить объем и площадь поверхности заданного конуса с основанием R и высотой h. Значения R и h заданы. Положить R=1 м , h=3 м. Отчет представить в виде распечатки рабочих листов, содержащих условие задачи, расчетные формулы, расчеты в Excel в режиме отображения данных и формул.
1. Расчетные формулы. (Формулы рекомендуется предварительно записать в тетрадь):
· площадь основания конуса
· площадь боковой поверхности
· площадь поверхности конуса
2. Создание рабочего листа с заданием и расчетными формулами.Порядок действий рекомендуется следующий:
· создать новый файл и сохранить его в личной папке под именем Конус.xls;
· в ячейку A1 ввести тему работы; в нижележащие ячейки (например, A3, A4) ввести номер примера и текст задачи;
· в отдельные ячейки A6:A7 и A10:A14 ввести обозначения размеров конуса с пояснениями; ввести данные: значения 1 и 3 для R и h соответственно в B6, B7;
· выполнить вставку расчетных формул с помощью приложения MS Equation 3.0.
Выполнение расчетов в Excel.
В ячейки E10:E14 последовательно ввести формулы:
Форматирование таблицы.
· Установить в таблице шрифт Times New Roman, размер 10.
· Расположить текст по образцу, используя команды: Формат|Ячейки, вкладка Выравнивание, флажки - Объединить ячейки и Переносить по словам. Если весь текст не виден в объединенных ячейках, нужно увеличить высоту строки.
· Выполнить подчеркивание заголовка, используя команду Формат|Ячейки|Шрифт|Подчеркивание одностороннее по значению.
Фрагмент рабочего листа Excel после форматирования представлен на рис. 2.1.
Пример 2. Вычислить по заданным формулам величины:
Решение
Решение выполним на одном рабочем листе с примером 1. Порядок действий аналогичен предыдущему примеру:
- введем условие задачи с формулами для вычислений;
- введем в отдельные ячейки обозначения и значения исходных данных m, c, t, b (см. рис. 2.2);
- в ячейки для результатов введем формулы:
Фрагмент рабочего листа с решением примера 2 представлен на рис.2.2.
Рис.2.2. Фрагмент рабочего листа для примера 2
При вводе формул, необходим тщательный анализ порядка действий и аккуратный набор всех символов. Возможно, количество ошибок сократится, если применить ряд приемов:
· при вставке ссылки на ячейку нужно щелкнуть мышью по этой ячейке;
· при вставке функции нужно вызвать Мастер функций по команде Вставка| Функция… (или кнопка Мастер функций), который позволяет выполнить вставку функции за два шага: первый шаг – выбор категории функции и выбор функции, второй шаг – задание аргументов функции.
Опишем эту технологию подробнее на примере первой формулы:
· для возведения в степень используем знак операции ^, поэтому основание степени нужно взять в скобки; соответственно, наберем =(
· введем значение m щелчком по ячейке A33 и знак умножения *
· вызовем Мастер функций, при этом появится диалоговое окно первого шага, представленное на рис. 2.3, выберем категорию функций Математические и в появившемся списке функций укажем TAN

Рис. 2.3. Диалоговое окно Мастера функций (первый шаг)

· при нажатии OK появится окно второго шага Мастера функций (см. рис. 2.4). В поле Число введем аргумент щелчком по ячейке со значением t C33. При нажатии OK или клавиши Enterввод функции заканчивается, заканчивается и ввод формулы в ячейку; для продолжения ввода в эту ячейку нужно нажать кнопку (Изменить формулу) в строке формул;

Рис. 2.4. Диалоговое окно Мастера функций (второй шаг)
· вставим функцию ABS. При задании аргумента наберем B33* и снова вызовем Мастер функций;
· функция от функции выбирается в списке функций в строке формул. Если требуемой функции нет в списке, нужно выбрать из списка вариант Другие функции, что приведет к повторному вызову Мастера функций. После знака умножения вставим функцию SIN. После задания аргумента нужно щелкнуть в строке формул (нажатие OK или клавиши Enter приведет к окончанию набора, а предложенный вариант вернет нас к окну внешней функции);
· после окончания ввода внешней функции ABS закончим ввод формулы, набрав закрывающую скобку и возведение в степень 0,5 – символы - )^0,5 или )^(1/2). Можно было также использовать функцию КОРЕНЬ, но это привело бы к тройному вложению функций в формуле и усложнению ее набора.
Оформление рабочего листа для печати
Команда Файл|Предварительный просмотр позволяет видеть фрагмент рабочего листа в виде, предназначенном для печати. Отметим, что обычно сетка для печатаемых документов не установлена. Установить сетку для печати можно по команде: Файл| Параметры страницы,вкладкаЛист,флажокСетка.
Показать заголовки строк и столбцов в печатаемом документе можно по команде Файл|Параметры страницы,вкладкаЛист,флажок Заголовки строк и столбцов. Как правило, этот флажок назначается вместе с сеткой.
Рабочие листы нужно разбить на страницы заданного размера. Способ разбиения и параметры страницы задается командой Файл|Параметры страницы. Задайте на вкладке - Размер бумаги - А4, на вкладке Поля – Левое –3 см, Правое, Верхнее и Нижнее по 2,5 см, на вкладке Лист- Последовательность вывода страниц Вниз, затем вправо.
Просмотрите и сохраните рабочую книгу, распечатайте отчет (рабочие листы книги) по команде Файл|Печать.
Варианты заданий
Каждый вариант содержит две задачи:
Задача 1. Вычислить объем и площадь поверхности заданного тела. Вычисления выполнить с точностью до третьего десятичного знака.
| Варианты задачи 1 | ||
| № | Заданное тело | Исходные данные |
| Доска в форме параллелепипеда из круглого бревна. | Радиус сечения R, длина L, толщина доски H. | |
| Половина куба, полученная при сечении куба диагональной плоскостью. | Ребро куба равно a. | |
| Пирамида с квадратом в основании. Вершина проектируется в центр квадрата. | Сторона квадрата в основании равна a,высота пирамиды равна H. | |
| Цилиндрический сосуд, закрытый полусферической крышкой. | Высота цилиндрической части H, радиус основания R | |
| Прямой круговой цилиндр. | Радиус основания R, высота H. | |
| Ангар в форме полуцилиндра, в основании которого находится прямоугольник | Стороны прямоугольника a и b. | |
| Прямая треугольная призма c равносторонним треугольником в основании. | Высота призмы h, сторона треугольника в основании a. | |
| Правильный тетраэдр (четырехгранник, пирамида с равносторонним треугольником в основании и равными ему боковыми гранями). | Ребро тетраэдра a. | |
| Прямой круговой конус. | Радиус снования R, образующая L. | |
| Октаэдр (восьмигранник), составленный из двух правильных четырехугольных пирамид. | Квадраты в основании со стороной a, высота каждой пирамиды H. | |
| Прямоугольный параллелепипед. | Стороны a, b, c. | |
| Прямой параллелепипед, т.е. в основании параллелепипеда произвольный параллелограмм, а третья сторона перпендикулярна основанию. | Стороны в основании a, b, угол между сторонами a, высота h. | |
| Полусфера. | Радиус R. | |
| Прямая шестигранная призма. | Высота призмы H, сторона шестиугольника в основания a. | |
| Усеченный конус. | Радиусы оснований: меньшего R1, большего R2 , высота h. |
Замечание.Все формулы для вычислений должны быть известны студентам первого курса или легко выводятся из основных теорем элементарной геометрии. Исключение может составить лишь усеченный конус. Приведем формулы для его объема и площади поверхности. Обозначения данных – в варианте 15, l – образующая конуса.
Задача 2. Вычислить данные выражения при заданных числовых значениях аргументов. Вычисления выполнить с точностью до четвертого десятичного знака.
Отчет должен представлять собой распечатанные листы рабочей книги с формулировкой задания, расчетными формулами и результатами. Расчеты требуется показать как в режиме отображения данных, так и в режиме отображения формул. Оформление страниц документа выполнить по образцу (см. приложение).
В данной статье, на простых примерах, описаны варианты использования функции ВПР MS Excel. Важные аспекты и возможные ошибки, которые возникают при использование данной функции. Функция ВПР в Excel.
Как вызвать функцию ВПР. Функция ВПР в Excel
В первую очередь разберемся, как вызвать данную функцию. Выбираем закладку Формулы. Находим кнопку Вставить функцию. И нажимаем ее. Так же, можно вызвать функцию ВПР, сочетанием клавиш Shift + F3.

Появляется диалоговое окно Вставка функции. В строке Поиск функции вводим ВПР. Нажимаем найти. По результатам поиска, в пункте Выберите функцию, появляется ВПР. Нажимаем на нее левой кнопкой мыши два раза или нажимаем ОК. Появляется непосредственно диалоговое окно функции ВПР – Аргументы функции.

Теперь перейдем непосредственно к вариантам применения функции ВПР.
Первый вариант использования функции ВПР.
Для примера возьмем две таблице. В одной Таблице №1 будет перечень с названиями конфет и будет указана их цена за кг. В другой, Таблица №2, тот же перечень, но с указанием их количества в кг. Наша задача добавить в Таблицу №2, в столбец Цена, цену конфет из Таблицы №1, чтобы в итоге получить стоимость. Названия конфет в разных таблицах находятся в разных местах, поэтому просто скопировать цену конфет с одной таблице в другую не получиться.

Перед тем, как вызвать функцию ВПР, выбираем нужную нам ячейку, в которой будет находиться наша формула функции и соответственно значение, которое мы хотим увидеть. В нашем случае это ячейка G3. Эта ячейка находиться в столбце Цена, Таблица №2. Функция ВПР позволит взять из Таблицы №1 цену Конфеты А и вставить эту цену в столбец Цена, Таблицы №2, напротив Конфеты А.
Вызываем функцию ВПР, как описано выше.
Аргументы функции. Функция ВПР в Excel.
Искомое_значение.
Значение поиска, которое должно быть найдена в указанном нами диапазоне, в строке Таблица. В нашем примере мы указываем Конфеты Ж (ячейка Е3, Таблица №2). Так как это значение идет первое в столбце Название конфет, Таблица №2. (Это не принципиально, но удобно). Это значение, которое будет искать наша функция в Таблице №1.
Что бы выбрать нужную нам ячейку с значением, достаточно просто стать курсором в строку Искомое_значение, а потом клацнуть левой кнопкой мыши, по нужной ячейке в таблице ( В нашем примере ячейка Е3).

Таблица.
![]()
Можно присвоить нашему диапазону имя, и прописать его в строке Таблица.
Как это сделать. Выбираем нужный нам диапазон. Таблица №1. Выбираем закладку Формулы, кнопка Задать имя. Нажимаем. Появляется диалоговое окно Создание имени. Пишем любое имя. Но нужно его запомнить. Например Конфеты. Нажимаем ОК.

![]()
В строке Таблица, вместо диапазона нужно будет ввести имя, которое мы присвоили – Конфеты
Номер_столбца.
Функция ВПР осуществляет поиск значение в самом левом столбце таблицы указанного диапазона поиска. Функция присваивает этому столбцу номер 1, по умолчанию. В нашем примере самый левый столбце, это Название конфет в Таблице №1. А в строке Номер_столбца, нам нужно указать, какой номер по порядку имеет столбец, из которого нужно перенести данные. В нашем примере это столбце Цена в Таблице №1. Он «второй» по порядку, если считать слева на право, от столбца Название конфет, Таблица №1. Поэтому в строку Номер_столбца мы пишем цифру 2. Если бы столбец Цена, Таблица №1 был бы расположен по порядку не на втором месте, а предположим на десятом, то мы соответственно указывали бы в строке Номер_столбца цифру 10.
![]()
Интервальный _просмотр.
В этой строке мы пишем цифру ноль «0». Это значит, что функция ВПР будет осуществлять поиск точных совпадений между значениями поиска (Искомое_значение) и значениями в крайнем левом столбце диапазона поиска (Таблица). В нашем примере поиск точных совпадений будет происходить между столбцом Название конфет, Таблица №1, и столбцом Название конфет в Таблице №2.
![]()
Если мы поставим цифру один «1», функция будет осуществлять поиск не точного совпадения, а приближенного к нашему критерию поиска.
Вот как это выглядит все вместе.

Протягиваем формулу по всему столбцу Цена в Таблице №2. Все цены перенесены с Таблице №1 в Таблицу №2.

Второй вариант использования функции ВПР.
У нас есть Таблица №1 и Таблица №2. Каждая таблица состоит из одного столбца. Для понимания алгоритма работы функции ВПР, в данном случае, таких простых таблиц достаточно. Столбцы содержат практически одинаковые данные. При этом, нам нужно сравнить их и узнать, какие данные есть в Таблице №2, но нет в Таблице №1.

Справа от Таблицы 2, в ячейку G3, вставляем функцию ВПР. Это расположение взято в качестве примера, можно использовать любой другой столбец и оформление.
В диалоговом окне, Аргументы функции прописываем следующие данные:
Искомое_значение. Это значение ячейки из Таблицы №2, наличие которой мы проверяем в Таблице №1. В нашем примере, это ячейка F3 (Значение 9).
Таблица. В данном случае мы указываем не диапазон всей таблицы, а только диапазон конкретного столбца, который мы сравниваем. Можно выделять столбец в таблице. А можно выделять весь столбец листа. В том случае, если в нем больше нет других данных. Вместо диапазона можно указать заданное имя столбца (Задаем имя).
Номер_столбца. Поскольку в таблице указан конкретный столбец, то здесь мы ставим цифру 1, так как искомое значение и данные, которые мы хотим перенести совпадают.
Интервальный _просмотр. Здесь ставим ноль «0», так как хотим, чтобы функция искала точные совпадения.


Можно проверить с точностью наоборот. И найти какие данные есть в Таблице №1 но нет в Таблице № 2.
Обратите внимание. Функция ВПР в Excel.
Функция ВПР осуществляет поиск значений (это значения, которые указаны в строке Искомое_значение) в первом (самом левом) столбец таблицы, диапазон которой указан в строке Таблица.

Это особенность, так же говорит нам о том, что значения, которые мы хотим перенести в нашу таблицу, должны быть справа, от столбца, в котором происходит поиск по заданному критерию.
Если в диапазоне Таблица указан один, конкретный столбец, то функция ВПР проверяет только его. И данное правило не обязательно.
Можно осуществлять поиск на разных Листах. Алгоритм работы такой же. Формула функции будет выгладить вот так: =ВПР(E6;Лист1!$B$1:$C$11;2;0). В нашем примере формулы функция ВПР расположена на Листе 2, а поиск значения и перенос данных с диапазона поиска происходит на Листе 1. Вместо диапазона можно использовать Заданное имя. Например Конфеты. Тогда формула функции будет выглядеть вот так: =ВПР(E6;Конфеты;2;0).
Возможные ошибки.
Цель работы: Освоить работу с электронными таблицами Excel на примере вычисления значений функции при различных значениях аргумента. Освоить понятия «абсолютной» и «относительной» ссылки.
Задание:
1. Открыть Excel и создать новый документ.
2. Заполнить столбец значений аргумента с заголовком.
3. Вычислить значения заданной функции во втором столбце.
4. Открыть второй лист.
5. Заполнить значения аргументов для функции двух переменных в два столбца.
6. Вычислить значение функции двух переменных в третьем столбце.
7. Открыть третий лист.
8. Заполнить значения аргумента x в первый столбец, начиная со второй строки, а значения аргумента y в первую строку, начиная со второго столбца.
9. Вычислить значения функции двух переменных.
10. Переименовать листы.
11. Сохранить документ.
Пример выполнения задания:
1.f(x)=x 2 +x+3, где x меняется от 0 до 5 с шагом 0,5.
2. F(x,y)=x 2 +y 2 –10, где x меняется от 0 до 4 с шагом 0,5, а y меняется от 0 до 4 с шагом 0,25.
1. Для выполнения задания 1 найдем в меню «Пуск» строчку «Программы», вы увидите выпадающее меню:

в котором надо выбрать строку .
В результате вы увидите окно, в котором уже открыт новый документ.
Если в окне нет документа или открыт чужой документ, необходимо выбрать пункт меню «Файл» и там найти команду «Создать. »:
Откроется новый документ.
Отметим, что чистый документ представляет из себя таблицу, у которой проименованы столбцы и пронумерованы строки. Имена столбцов задаются латинскими буквами в алфавитном порядке до столбца с именем Z, следующий столбец имеет имя AA, затем AB, AC и т.д.
Примечание.Если имена ячеек задаются в виде R1C1, изменить на латинский алфавит можно с помощью \Сервис\Параметры… , там выбрать закладку «Общие» и убрать флажок из поля «Стиль ссылок R1C1» в разделе «Параметры».
В остальном оформление окна не отличается от окна Word, за исключением строки формул:
Слева в ней указывается адрес активной ячейки, справа набираются формулы начиная со знака «=», а также имеется ряд кнопок:
, которая вызывает встроенные функции Excel и присутствует всегда;

, которая стирает формулу из строки формул;

– вычисляет формулу.
Примечание. Рассматривать работу с панелью инструментов «Стандартная» и «Форматирование» не будем, так как обе эти панели подробно разобраны в пособии «Лабораторный практикум. Часть 1. Word». Отметим только, что применять форматирование к ячейкам можно или до набора в них текст, или к уже набранному тексту. Для этого надо выйти из режима набора текста в ячейку (щелчок левой кнопки мыши на любой другой ячейке) и установить на нее курсор ячейки, теперь можно применять форматирование.
В Excel имеется несколько видов курсоров, рассмотрим их все:
ê – текстовой курсор, позволяющий набирать текст в ячейки строку формул.
– курсор мыши, позволяющий производить выбор и выделение ячеек.
+ – курсор мыши, позволяющий производить копирование функций, появляется в нижнем правом углу выделенной (рабочей) ячейки (на маленьком квадратике).

– курсор ячейки.
– курсор мыши, позволяющий перемещать ячейки.
и – курсоры мыши, позволяющие расширять строки и столбцы. Появляются только в заголовке столбцов и нумерации строк.
и – курсоры мыши, позволяющие выделять целиком столбец или строку.
2. Теперь мы можем начать работать в Excel.
Заполним столбец значений аргумента x, который изменяется от 0 до 5 с шагом 0,5.
Это можно сделать несколькими способами:
Способ 1. В ячейка А1 запишем «x» и отформатируем его по центру. В ячейку А2 запишем 0. В ячейку А3 – 0,5. В ячейку А4 – 1 и т.д. до ячейки А12, в которую записывается 5.
Способ 2. В ячейку А1 запишем «х» и отформатируем его по центру. В ячейку А2 запишем 0. В ячейку А3– 0,5. Затем выделим ячейки А2 и А3, установим курсор мыши в нижний правый угол (он примет вид «+»), нажмем левую кнопку мыши и, удерживая ее, перемещаем до ячейки А12включительно. (Отметим, что справа от курсора появляется желтенький прямоугольник, в котором при движении мыши меняются цифры. Эти цифры указывают значение в ячейке, мимо которой движется указатель мыши.) Данный способ эффективен, если параметр изменяется с постоянным шагом.

Способ 3. В ячейку А1 запишем «х» и отформатируем его по центру. В ячейку А2 запишем 0. В ячейку А3 установим курсор и наберем формулу:
=А2+0,5
нажмем Enter. Затем установим курсор ячейки на А3, а курсор мыши – на нижний правый угол («+») и, удерживая левую кнопку мыши, растянем до А12.
В результате получим:
3. Вычислим значения заданной функции f(x)=x 2 +x+3.
Для этого в ячейке В1 наберем текст «f(x)» и центрируем его. В ячейку В2 наберем формулу:
т.е. вместо «х» вы набираете адрес ячейки, в которой находится соответствующий аргумент.
Затем, установив курсор мыши в нижний правый угол (+), растяните формулу до ячейки В12.
В результате получим:
Как видите, курсор мыши стоит на ячейке В2, а в строке формул указаны адрес этой ячейки и формула, набранная в ней, так можно просмотреть все формулы в столбце В.
Вы можете заметить, что формулы отличаются только номером строки, в остальном они одинаковы.
Примечание. Если растягивать формулу вниз или вверх, то изменяется номер строки, а если растягивать формулу вправо или влево, то изменяется буква столбца.
4. У Excel есть еще одно отличие от редактора Word. Каждый документ Excel состоит из нескольких отдельных листов,выполняющих роль отдельных документов, но при этом с возможностью ссылки друг на друга. Закладки листов находятся в нижней части окна Excel, сразу над строкой состояния:
Вычислим функцию двух переменных на листе 2. Для этого откроем второй лист (щелкнув левой кнопкой мыши на закладке «Лист2»).
5. Заполним значения аргумента в столбцах А и В. Напомним, что у функции двух аргументов при одном значении х может быть много различных значений y.
В ячейку А1 запишем «х» по центру. В ячейку В1 – «y» по центру. В ячейку А2– 0. В ячейку В2 – 0. В ячейку А3 – 0. В ячейку В3 – 0,25.
Теперь выделим четыре ячейки от А2 до В3, установим курсор мыши в нижний правый угол и, удерживая левую кнопку мыши, растягиваем до строки 18 включительно, получим:
Теперь посчитаем для второго значения х. В ячейкуА19 набираем 0,5. В ячейку В19 – 0. В А20 – 0,5. В В20 – 0,25. Выделяем ячейки А19–В20 и растягиваем черным крестиком (+), получаем:
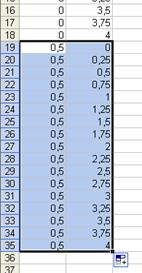
И так заполним для каждого х до значения 4 с шагом 0,5. Вы получите длинную таблицу из 154 строк.
Примечание. Отметим, что если вы растянули недостаточно или, наоборот, слишком много, то, пока не снято выделение с ячеек, вы можете увеличить или уменьшить таблицу вычислений, взявшись за нижний правый угол всего выделения и потянув вниз или вверх.
6. Вычислим функцию f(x,y)=x 2 +y 2 –10 в третьем столбце. Для этого в ячейку С1 наберем «f(x,y)» и центрируем. В ячейку С2 наберем:
и вычислим формулу.
После чего растянем формулу за нижний правый угол и получим:
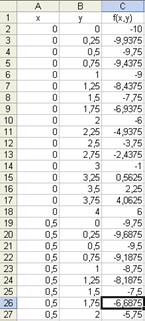
7. Теперь откроем лист 3, для этого надо щелкнуть левой кнопкой мыши по закладке «Лист3».
8. Заполним значения аргумента для функции двух переменных, только теперь значения х расположим в столбец, а значения y – в строку.
Ячейку А1 оставим пустой. В ячейку А2 запишем 0.
В А3 – 0,5. Теперь выделим ячейки А2и А3 и растянем за нижний правый угол до строки 10.
Заполняем значения y. Для этого в ячейку В1 запишем 0. В С1 – 0,25. Выделим ячейки В1и С1, а далее растянем за нижний правый угол до ячейки R1. Мы получили:
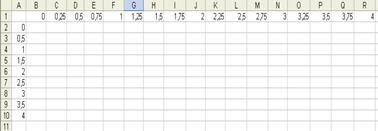
9. Теперь заполним значения функции в ячейку В2:
Вычислим ее. Но теперь, поскольку ссылки у нас относительные, если мы будем растягивать формулу, то при растягивании вниз у нас будут смещаться ссылки для значений y, а при растягиванию вправо будут смещаться буквы в ссылках значений х.
Нам необходимо зафиксировать в ссылках для х столбец А (сделать абсолютную ссылку на столбец А), а в ссылках для y – строку 1 (сделать абсолютную ссылку на строку 1). Для того чтобы фиксировать строки и столбцы в ссылках, в Excel предназначен знак «$». Тогда в нашей формуле правильно записать ссылки для х – $A2, а ссылки для y – B$1. Мы получим:
Вот эту формулу уже можно растянуть. Заметим, что растягивать по диагонали нельзя, данное действие выполняется в два приема: сначала растягивают вниз и отпускают кнопку мыши, далее, не снимая выделения, снова берут за нижний правый угол и растягивают вправо. В результате получаем:
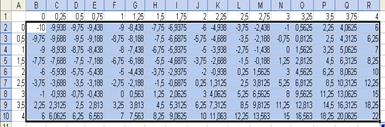
10. Теперь переименуем листы Excel. Для этого установим курсор на закладку «Лист1» и щелкнем один раз правой кнопкой мыши, получим контекстное меню вида:
в котором выберем пункт «Переименовать» и запишем туда «f(x)».
Повторим процедуру для второго и третьего листа, назвав их «f1(x,y)» и «f2(x,y)» соответственно. Мы получим:
11. Для сохранения документа выполним одно из следующих действий:
· \Файл\Сохранить… В открывшемся окне в поле «Папка» указываем диск и папку, куда сохраняем файл. В поле «Имя» набираем имя сохраняемого документа. Нажимаем кнопку «Сохранить».
Нажимаем кнопку на панели инструментов «Стандартная» и в полученном окне проводим вышеуказанные действия.
Порядок вычислений по формуле: =3+5*COS(B4)-2*A2:
2.4. ПРАКТИЧЕСКАЯ РАБОТА
Пример 1. Вычислить объем и площадь поверхности заданного конуса с основанием R и высотой h. Значения R и h заданы. Положить R=1 м , h=3 м. Отчет представить в виде распечатки рабочих листов, содержащих условие задачи, расчетные формулы, расчеты в MS Excel в режиме отображения данных и формул.
1. Расчетные формулы :

образующая l = h 2 + R 2
площадь основания конуса
площадь боковой поверхности
площадь поверхности конуса
объем конуса V = 1 3 S 0 h
2. Создание рабочего листа с заданием и расчетными формулами.
Порядок действий рекомендуется следующий :
− создать новый файл и сохранить его в личной папке под именем Конус.xls;
− в ячейку A1 ввести тему работы; в нижележащие ячейки (например, A3, A4) ввести номер примера и текст задачи;
− в отдельные ячейки A6:A7 и A10:A14 ввести обозначения размеров конуса с пояснениями; ввести данные: значения 1 и 3 для R и h соответственно в
− выполнить вставку расчетных формул с помощью приложения
3. Выполнение расчетов в MS Excel.
В ячейки E10:E14 последовательно ввести формулы: =КОРЕНЬ(B6*B6+B7*B7)
=ПИ()*B7*E10 =E11+E12 =E11*B6/3.
4. Форматирование таблицы.
Установить в таблице шрифт Times New Roman , размер 10. Расположить текст по образцу, используя кнопки вкладки Главная .
Если весь текст не виден в объединенных ячейках, нужно увеличить высоту строки.
Выполнить подчеркивание заголовка, используя команду Формат ячейки|Шрифт | Подчеркивание одностороннее по значению контекстно-
зависимого меню (правая копка мыши).
Фрагмент рабочего листа MS Excel с решением примера 1 представлен на рис. 2.1.
Вычисленияпоформуламсиспользованиемвстроенныхматематических 1 функций
4 основанияc точностьюдочетвертогодесятичногознака
Рис. 2.1. Фрагмент рабочего листа Excel для примера 1
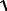
Пример2. Вычислить по заданным формулам величины: f = m tgx + c sin t , z = log 2 m cos bt e t + c
при заданных значениях m = 2; c = − 1; t = 1,2; b = 0,7
Решение выполним на одном рабочем листе с примером 1. Порядок действий аналогичен предыдущему примеру:
− введем условие задачи с формулами для вычислений;
− введем в отдельные ячейки обозначения и значения исходных данных m, c, t, b (см. рис. 2.2);
− в ячейки для результатов введем формулы:
Фрагмент рабочего листа с решением примера 2 представлен на рис.2.2.
Вычислить по заданным формулам
z = log 2 m cos bt e
m = 2, c = − 1, t = 1,2 b = 0,7
Рис.2.2. Фрагмент рабочего листа для примера 2
При вводе формул, необходим тщательный анализ порядка действий и аккуратный набор всех символов. Возможно, количество ошибок сократится, если применить ряд приемов:
• при вставке ссылки на ячейку нужно щелкнуть мышью по этой ячейке;
• при вставке функции нужно вызвать Мастер функций (вкладка Формулы, кнопка Вставить функцию ) , который позволяет выполнить вставку функции за два шага: первый шаг – выбор категории функции и выбор функции, второй шаг – задание аргументов функции.
Опишем эту технологию подробнее на примере первой формулы:
• для возведения в степень используем знак операции ^, поэтому основание степени нужно взять в скобки; соответственно, наберем =(
• введем значение m щелчком по ячейке A33 и знак умножения *
• вызовем Мастер функций , при этом появится диалоговое окно первого шага, представленное на рис. 2.3, выберем категорию функций Математические и в появившемся списке функций укажем TAN
Рис. 2.3. Диалоговое окно Мастера функций (первый шаг)

• при нажатии OK появится окно второго шага Мастера функций (рис. 2.4). В поле Число введем аргумент щелчком по ячейке со значением t C33. При нажатии OK или клавиши Enter ввод функции заканчивается, заканчивается и ввод формулы в ячейку; для продолжения ввода в эту ячейку нужно нажать кнопку ( Изменить формулу ) в строке формул;
Рис. 2.4. Диалоговое окно Мастера функций (второй шаг)
• вставим функцию ABS . При задании аргумента наберем B33* и снова вызовем Мастер функций ;
• функция от функции выбирается в списке функций в строке формул. Если требуемой функции нет в списке, нужно выбрать из списка вариант Другие функции , что приведет к повторному вызову Мастера функций . После знака умножения вставим функцию SIN . После задания аргумента нужно щелкнуть в строке формул (нажатие OK или клавиши Enter приведет
к окончанию набора, а предложенный вариант вернет нас к окну внешней функции);
• после окончания ввода внешней функции ABS закончим ввод формулы, набрав закрывающую скобку и возведение в степень 0,5 – символы - )^0,5 или )^(1/2). Можно было также использовать функцию КОРЕНЬ , но это привело бы к тройному вложению функций в формуле и усложнению ее набора.
2.4.2. ВАРИАНТЫ ЗАДАНИЙ
Вычислить данные выражения при заданных числовых значениях аргументов. Вычисления выполнить с точностью до третьего десятичного знака.
v = (1 − y ) 2 /(1 − cos 2 y ); x = 7,3; y = 0,3
l = k m − 1 + ln( x 3 − y ) +
m = 3; x = 4,7; y = 5,8; z = 4,9
1. z = 2,58 ( x 3 − 1 ) − ln ( x 2 + 3 ) ; , x = 5,1
cos ( α 2 + β ) − sin α
v = ln| x − a | 8,055; x = 0,2; a = 2,72
l = m k + 1 − tg ( k + 1,8 ) − 1
z = 0,082 x 3 + e x + 1 ; x = 1,53
z = [ lg ( y 3 + 7,51 ) − y ] /
z = tg ( x 2 + y 3 ) / [ cos 2 ( x 2
+ y ) − cos x ] ; x = π / 3;
u = lg 2 ( x − 1 ) ; A = 9,5 ( y 0,3 − e x ); x = 5,85; y = 21,3
z = x 1/ 2 + (3,37 x + 2,03) 2 ;
cos( w − 1) + ln( w 2 + 3)
tg 2 ( α − β ) + cos 2 α
t = ln( a 1/ 2 + e x ); x = 15,73; a = 4,25
sin( x − 1) + lg( x 2 − 1)
tg ( α − β ) + cos 2 α
; t = ln( a 1/ 2 + x 1/ 3 );
x = 18,08; a = 11,75
l = k m − n + cos 2 ( m + n x ) −
z = 2.198 x 2 − ( x
cos x 2 − sin 2 y
l = m k − 1 − ctg ( m − k ) −
z = 0,65( x 2 − 2) + x 1/ 3 ;
z = ( e x − 1,2 + e 1,2 + x ) / ln (0,1 t );
; m = 3; k = 2; z = 0,3
z = (8,59 − x 1/ 3 ) − (1 − ln x );
+ 1) + e x − 1 ] /( x 2
z = [ tg ( α − β ) 2
− 1 ] / cos 2 ( γ − 1);
cos 2 ( t − 1) / sin( t + 1)
u = 1,4; a = 0,8; t = 3,8
z = 2,58 ( x 3 − 1 ) − ln ( x + 1 ) ;
cos ( α 2 + β ) − sin
v = 12,35 ln| x − a |;
l = m k − 1 − tg ( m + k ) −
3. ЛОГИЧЕСКИЕ ФУНКЦИИ MS EXCEL
3.1. ОСНОВНЫЕ ПОНЯТИЯ
Логическое выражение - это высказывание, принимающее значения ИСТИНА или ЛОЖЬ. Логические выражения в MS Excel позволяют выполнять вычисления, зависящие от условий. Условие считается выполненным, если значение соответствующего ему логического выражения - ИСТИНА, и не выполненным, если значение логического выражения - ЛОЖЬ.
Логическое выражение может содержать знаки равенств и неравенств и логические функции. Равенства и неравенства применяются к двум операндам (сравниваются две величины).
Пусть, например, в MS Excel требуется проверить истинность неравенств:
a 2 + b 2 = 4, z ≠ z 0 ,
им могут соответствовать логические выражения в MS Excel:
LN ( B 3 + 1/ 2) >= 2,
A 5^2 + A 6^2 = 4, C 10 <> $ A $5.
В данном примере величины, обозначенные буквами, помещены в некоторые ячейки. Ссылка на ячейку $A$5 является абсолютной, показывая постоянство величины z 0
Пара символов < > означает - «не равно», смысл остальных символов очевиден. На равенство можно проверить и текстовое значение, причем текст в выражении заключается в кавычки.
Как правило, значение логического выражения меняется в зависимости от конкретных значений входящих в него переменных и может быть использовано в наиболее важной функции категории Логические – функции ЕСЛИ . Другие логические функции НЕ, И, ИЛИ – используются для задания сложных условий. Логические значения ИСТИНА и ЛОЖЬ могут задаваться в MS Excel как функции. Итак, перечислены все логические функции. Далее рассмотрен их синтаксис и примеры применения.
3.2. ЛОГИЧЕСКИЕ ФУНКЦИИ ЕСЛИ, И, ИЛИ, НЕ
Логическая функция ЕСЛИ имеет вид:
где x1, x2, x3 – аргументы, здесь x1 - логическое выражение, x2, x3 – любые выражения, разрешенные вMS MS Excel; причем вычисляется x2 , если x1 имеет значение ИСТИНА , и x3 , если x1 имеет значение ЛОЖЬ . Если третий аргумент функции не определен, то ошибки в записи функции нет – в этом случае ей присваивается значение ЛОЖЬ , если условие не выполнено. Если ничего не нужно вычислять при невыполнении условия, следует в качестве третьего аргумента задать пробел как текст.
Примеры: ЕСЛИ(A5>0;LN(A5);-1); ЕСЛИ(B2< >0;1/B2;” ”)
Логическая функция И имеет вид:
где x1; x2;; …;xn – аргументы, являющиеся логическими выражениями. Функция может содержать до 30 аргументов. Функция И
принимает значение ИСТИНА , если все ее аргументы истинны, в противном случае она принимает значение ЛОЖЬ .
Логическая функция ИЛИ имеет вид:
где x1; x2;; …;xn –аргументы, являющиеся логическими выражениями. Функция может содержать до 30 аргументов. Функция ИЛИ принимает значение ИСТИНА , если хотя бы один из ее аргументов есть ИСТИНА , в противном случае она принимает значение ЛОЖЬ .
Логическая функция НЕ имеет вид НЕ(x),
где x – логическое выражение. Ее значение ИСТИНА , если x имеет значение ЛОЖЬ , и наоборот.
3.2. ПРАКТИЧЕСКАЯ РАБОТА
Пример 1. Вычислить величину y при заданном значении x
3 x 2 , если x < 2 y = 4
В ячейки рабочего листа A1,B1 вводим обозначения x, y
В ячейку A2 вводим значение x
В ячейку B2 вводим формулу:
1-й способ . =ЕСЛИ(A2<2;3*A2*A2/4;3/(2*A2)), которая работает следующим образом – если в ячейке A2 число меньшее 2, то вычисляется выражение 3*A2*A2/4; если содержимое A2 больше или равно 2, то вычисляется 3/(2*A2).
2-й способ . Ввод формулы можно выполнить и с помощью Мастера функций. На первом шаге мастера из категории Логические выбираем функцию ЕСЛИ . На втором шаге заполняем поля аргументов, как показано в окне второго шага Мастера функций (рис. 3.1)

.
Читайте также:



