Visual studio математические выражения
Основные математические операторы
- Сложение (+)
- Вычитание (-)
- Умножение (*)
- Деление (/)
- Остаток от деления (%)
Рассмотрим пример простейшего приложения:
namespace ConsoleApp1
class Program
static void Main(string[] args)
// Настройка кодировки, если используется Английская версия Windows.
Console.OutputEncoding = Encoding.Unicode;
// Запрашиваем у пользователя входные данные.
var first = InputNumber();
var second = InputNumber();
// Сумма.
var sum = first + second;
Console.WriteLine($"Результат сложения и равен .");
// Разность.
var sub = first - second;
Console.WriteLine($"Результат вычитания и равен .");
// Умножение.
var mul = first * second;
Console.WriteLine($"Результат умножения и равен .");
// Деление на цело.
var dev = first / second;
Console.WriteLine($"Результат деления на цело и равен .");
// Дробное деление.
var devd = (double)first / second;
Console.WriteLine($"Результат деления дробного и равен .");
// Остаток от деления.
var mod = first % second;
Console.WriteLine($"Результат остатка от деления и равен .");
// Ожидаем ввода пользователя.
Console.ReadLine();
>
/// <summary>
/// Запросить у пользователя на ввод целое число.
/// </summary>
/// <returns> Целое число, введенное пользователем. </returns>
private static int InputNumber()
// Повторяем запрос до тех пор, пока пользователь ни введет корректные данные.
while (true)
// Делаем запрос на консоль и сохраняем введенные пользователем данные в текстовом формате.
Console.Write("Введите число: ");
var input = Console.ReadLine();
// Пробуем преобразовать введенные пользователь данные в целое число.
if (int.TryParse(input, out int inputNumber))
// Если преобразование удалось, то возвращаем результат.
return inputNumber;
>
// Иначе сообщаем пользователю об ошибке.
Console.WriteLine("Некорректный ввод. Пожалуйста, введите целое число.");
>
>
>
>
Исходный код достаточно тривиален, но мне хотелось бы остановиться на нескольких важных моментах. В первую очередь это операция деления. Как вы видите, он а представлена дважды. С помощью одного и того же символа обозначаются две различные операции:
- При целочисленном делении дробная часть просто отбрасывается, и результатом всегда является целое число. Для того, чтобы деление было целочисленным, необходимо, чтобы оба оператора в операции деления были целочисленными.
- При дробном делении результатом является число с целой и дробной частью. Разделителем является точка. Для того, чтобы деление было дробным, достаточно чтобы хотя бы один из операторов был с плавающей или фиксированной запятой.
Так же стоит упомянуть операцию остатка от деления, про которую многие забывают. В других языках она часто записывается как mod. Она означает, что результатом будет число, оставшееся неподеленным при целочисленном делении. Для примера 5 % 2 = 1, это означает, что было выполнено целочисленное деление ближайшего меньшего подходящего числа - 4. А результатом является разница этого числа и исходного 5 - 4 = 1.
Операторы инкремента
Существует особая группа операторов, которая называется инкрементной. Особенность этих операторов заключается в том, что они изменяю значение которое хранится в самой переменной. Вот наиболее часто используемые инкрементные операторы:
- Увеличение значения переменной на 1 (++)
- Уменьшение значения на 1 (--)
- Увеличение значения переменной на заданное значение (+=)
- Уменьшение переменной на заданное значение (-=)
- Умножение переменной на значение (*=)
- Деление переменной на значение (/=)
С точки зрения работы приложения все приведенные ниже записи являются идентичными, но инкрементные операторы являются более компактными при написании исходного кода приложения.
Или другой пример, когда если мы хотим умножить текущее значение переменной на 4, то это можно записать так:
Префиксная и постфиксная запись инкремента
Обратите внимание, что существуют две формы записи:
- Префиксная - когда оператор инкремента ставится перед именем переменной (++i)
- Постфиксная - когда оператор инкремента ставится после имени переменной (i++)
В большинстве случаев разницы нет, но в некоторых специфических случаях разница существует. Рассмотрим пример кода:
namespace ConsoleApp1
class Program
static void Main(string[] args)
int n = 0;
int m = 0;
Рассчитать значения x , определив и использовав соответствующую функцию:
Соображения
Если внимательно посмотреть на выражение, то можно заметить схожесть между каждым его слагаемым. В общем случае каждое слагаемое можно представить выражением
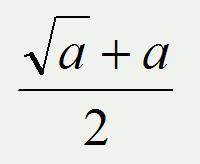
где a – некоторое число. В нашем случае a = 6, 13, 22.
Поэтому, целесообразно реализовать функцию, которая получает входным параметром переменную a и вычисляет данное выражение.
Выполнение
1. Запустить MS Visual Studio . Создать проект по шаблону Windows Forms Application
После загрузки MS Visual Studio нужно создать проект по шаблону Windows Forms Application . Подробный пример создания проекта по шаблону Windows Forms Application описывается в теме:
Следует напомнить, что проект создается командой
Рис. 1. Окно создания нового проекта
После выбора OK система создаст новую форму, как показано на рисунке 2.

Рис. 2. Форма приложения после создания
2. Проектирование основной формы
2.1. Размещение элементов управления на форме
В соответствии с условием задачи, в программе ничего не вводится, только проводится расчет на основе известных значений. С учетом этого, на форме размещаются следующие элементы управления:
- один элемент управления типа Label . Автоматически создается объект (переменная) класса Label с именем label1 . С помощью этого имени можно иметь доступ к результату;
- один элемент управления типа Button . Автоматически создается объект с именем button1 . Этот элемент управления будет выводить текст условия задачи;
- один элемент управления типа PictureBox (см. рис. 3). Этот элемент управления используется для визуализации сложной формулы. Формула представляется в виде файла с расширением *.jpg . В результате создается объект с именем pictureBox1 ;
- один элемент управления типа Label в нижней части формы. Этот элемент управления будет выводить результат.
После размещения элементов управления Label , Button , PictureBox форма программы будет иметь вид, как показано на рисунке 3.

Рис. 3. Форма приложения после размещения элементов управления
2.2. Настройка элементов управления Form , Label , Button
Нужно настроить следующие свойства элементов управления:
Дополнительно можно настроить другие свойства по собственному усмотрению.
2.3. Настройка элемента управления PictureBox
Поскольку элемент управления PictureBox предназначен для отображения рисунка на форме, то сначала нужно выбрать этот рисунок. Это осуществляется кликом мышкой на стрелке вправо в верхнем правом углу PictureBox, как показано на рисунке 4.

Рис. 4. Выбор меню задач PictureBox
В нашем случае файл с формулой можно взять здесь . Этот файл был подготовлен раньше с помощью графического редактора.
После выбора файла рисунка форма приложения будет иметь вид, как показано на рисунке 5.

Рис. 5. Форма приложения после загрузки файла рисунка
- активировать (выделить) элемент управления PictureBox ;
- с помощью мышки увеличить ширину окна PictureBox ;
- свойство SizeMode установить в значение StretchImage (масштабирование) как показано на рисунке 6.
Возможен и другой вариант настройки отображения формулы с помощью свойства SizeMode .
Рис. 6. Форма приложения после настройки и свойство SizeMode
3. Добавление текста функции к программному коду
3.1. Добавление текста функции в модуль Form1.h
Поскольку, вся работа выполняется в одной форме, то и реализация тела функции будет внутри кода класса Form1 .
Таким образом, в нижнюю часть тела класса Form1 нужно добавить следующий программный код
В теле функции используется функция Sqrt() , которая вычисляет корень квадратный.
На данный момент текст класса Form1 в сокращенном виде следующий:
В нашем случае, обработчик события будет иметь следующий вид:
Теперь можно запускать программу на выполнение. На рисунке 7 изображен результат выполнения программы
Используемые программы и библиотеки
Построение дерева выражения
Парсер-генератор GOLD я выбрал, поскольку уже имею опыт с ANTLR и захотелось чего-то нового. Ну а его преимущества, по сравнению с остальными, вы можете увидеть в данной таблице. Как видим, если сравнивать с ANTLR, то GOLD основан на алгоритме LALR, а не LL. А это значит, что в теории, сгенерированный парсер быстрее и мощнее, но с другой стороны, его нельзя отлаживать (в GOLD вообще подгружается файл в бинарном формате), а если бы и можно было бы, то это было бы совсем не очевидно и неудобно. Другим большим отличием является форма задания грамматики: BNF, а не EBNF. А это означает, что грамматика, записанная в данной форме, имеет немного больший размер из-за угловых скобок, знака определения и отсутствия условных вхождений и повторений (подробней в wiki. И, например, такое правило в EBNF, как
будет переписано в такой форме:
Итак, окончательная грамматика математических выражений имеет следующий вид:
В грамматике вроде бы все очевидно, за исключением лексемы: Number1 = +('.'*('('*')')?)? Данная конструкция позволяет парсить строки следующего вида: 0.1234(56), что означает рациональную дробь: 61111/495000. Про преобразование такой строки в дробь я расскажу позже.
- Calculated — узел, представляющий рассчитанную константу в приемлемом для компилятора формате double, например «0.714285714285714», «0.122222222222222». Для каждой такой константы создается новый объект, даже если они одинаковые.
- Value — узел, представляющий рассчитанную константу в формате рациональной дроби, т.е. 1 представляется как «1/1», «0.1(2)» — как «11/90», «0.1234» — как «617/5000». Для каждой такой константы создается новый объект, даже если они одинаковые.
- Constant — узел, представляющий неопределенную константу, например «a», «b» и др. Если в выражении встречаются две таких константы, то они указывают на один узел.
- Variable — узел, представляющий переменную, например «x», «y» и др. Если в выражении определенная переменная встречается несколько раз, то для нее создается только один объект, так же как и для неопределенной константы. Важно понимать, что разграничение константы и переменной важно только на этапе вывода аналитическое производной, а в других случаях это знание не обязательно.
- Function — узел, представляющий функцию, например "+", «sin», "^" и другие. Единственный узел, который может иметь потомков.
Из грамматики видно, что узлы полученного дерева либо не имеют детей (например, значения или переменные), либо имеют от одного до двух детей в случае стандартных функций (например, cos, сложение, возведение в степень). Все остальные функции могут иметь бОльшее количество аргументов, но они не рассматривались.
Таким образом, все узлы (а точнее узлы с функциями) имеют от 0 до 2 детей включительно. Это верно с теоретической точки зрения. Но на самом деле пришлось сделать так, чтобы функции "+" и "*" имели неограниченное количество детей для того, чтобы облегчить задачу симплификации, которая будет рассмотрена позже. Кстати, от таких бинарных операций, как "-" и "/" тоже пришлось отказаться по таким же причинам (они были заменены на сложение с отрицанием правой части и умножением с обращением правой части).
Итак, на этапе разбора все узлы для каждого правила попадают или извлекаются из буфера, который называется Nodes. Таким образом, в конце всего процесса в этом буфере остается одна или несколько функций с правой и левой частью. Также в процессе парсинга для того, чтобы функции сложения и умножения сразу создавались мультинарными, использовались дополнительные буферы ArgsCount и ArgsFuncTypes, хранящие текущее количество аргументов в функции и тип текущей функции соответственно. Таким образом, например для функции умножения, используется данный код:
Обработка первого множителя:
Обработка i-того множителя:
Обработка последнего множителя:
Из этого кода видно, что, например, если никакого умножения и нет, то последнюю функции умножения с нулевым количеством элементов нужно удалить с помощью PushOrRemoveFunc. Аналогичные действия нужно провести и для сложения.
Обработка функций одного аргумента, бинарных функций, констант, переменных и значений является тривиальной, и это все можно посмотреть в MathExprParser.cs.
Вычисление аналитической производной
На данном этапе нужно преобразовать функцию в ее производную.
Как известно из первого этапа, в созданном дереве выражения существуют только четыре типа узлов (пятый появляется позже). Для них и определим производную:
- Value' = 0
- Constant' = 0
- Variable' = 1
- Function' = Derivatives[Function]
Стоит отметить, что все производные не записано жестко в коде, а тоже могут вводиться и парситься динамически.
В этом списке нет сложения и умножения потому что, как упоминалось выше, это функции с несколькими аргументами. А для того, чтобы парсить такие правила, необходимо было бы еще написать много кода. По этим же причинам, здесь нет композиции функций, т.е. (f(g(x)))' = f(g(x))' * g(x)', а вместо этого все функции представлены как композиции функций.
Также, если для функции не найдена подстановка в Derivatives (т.е. неопределенная функция), то она просто заменяется на функцию со штрихом: т.е. f(x) превратится в f(x)'.
После того, как аналитическая производная успешно была получена, возникает проблема, которая заключается в том, что в получившееся выражении возникает очень много «мусора», такого как a + 0, a * 1, a * a^-1 и пр., а также получившееся выражение можно вычислить более оптимальным образом. Например, даже для простого выражения получится некрасивое выражение:
Для устранения таких таких недостатков используется упрощение.
Упрощение (симплификация) выражения
На этом этапе, в отличие от этапа вычисления производных, я не стал записывать правила симплификации в отдельном месте, для их последующего его разбора из-за того, что функции сложения и умножения являются функциями нескольких аргументов, что представляет определенную сложность в создании таких правил в контексте итеративного языка.
В начале топика я затронул тему про то, почему сложение и умножение представлено в виде n-арных функций. Представим ситуацию, изображенную на картинке ниже. Здесь видим, что a и -a сокращаются. Но как это сделать в случае бинарных функций? Для этого нужно перебирать узлы a, b и c, чтобы потом обнаружить, что a и -a являются детьми одного узла, а значит их можно сократить вместе с узлом. Но, понятное дело, что перебор деревьев это не такая простая задача, так как куда проще производить все действия в цикле сразу со всеми детьми, как это представлено на рисунке справа. Кстати, такой перебор нам позволяют сделать математические свойства ассоциативности и коммутативности.
 |  |

Во время процесса симплификации возникает задача сравнения двух узлов, которые, в свою очередь, могут иметь один из четырех типов. Это нужно, например, для того, чтобы сократить такие выражения как sin(x + y) и -sin(x + y). Понятно, что можно по узлам сравнить сами узлы и все их потомки. Но проблема заключается в том, что данный метод не справится с ситуацией, когда слагаемые или множители переставлены местами, например sin(x + y) и -sin(y + x). Для разрешения данной проблемы используется предварительная сортировка слагаемых или множителей, для которых выполняется свойство коммутативности (т.е. для сложения и вычитания). Сравниваются узлы так, как показано на картинке ниже, т.е. значения меньше констант, константы меньше переменных и т.д. Для функций все немного сложнее, поскольку нужно сравнить не только их названия, но и количество аргументов и сами аргументы.
Таким образом, после всех вышеописанных преобразований и переборов, исходное выражение неплохо упрощается.
Обработка рациональных дробей
Компиляция выражения
Для преобразования полученного семантического дерева в код IL после этапа симплификации, я использовал Mono.Cecil.
В начале процесса создается сборка, класс и метод, в который будут записываться команды. Потом для каждого FuncNode рассчитывается, сколько он раз встречается в программе. Например, если есть функция sin(x^2) * cos(x^2), то в ней функция возведения x в степень 2 встречается два раза, а функции sin и cos — по одному. В дальнейшем, данная информация о повторах вычислений функций используется следующим образом (т.е. таким образом второго раза вычисления одной и той же функции не происходит):
- Ldarg — Операция загрузки определенного аргумента функции в стек.
- Ldc_R8 — Загрузка определенного значения double в стек.
- Stloc.n — Извлечение из стека последнего значения и его сохранение в локальную переменную n.
- Ldloc.n — Помещение локальной переменной n в стек.
Стоит отметить, что данные оптимизации применимы в случае отсутствия ветвления в коде, и это очевидно почему (если не совсем очевидно, то предлагаю поразмыслить). Но так как код математических функций и их производных не может содержать циклов в моем случае, то это все работает.
Быстрое возведение в степень
Я думаю, что почти все знают про алгоритм быстрого возведения числа в степень. Но ниже представлен данный алгоритм на уровне компиляции:
Алгоритм быстрого возведения в степень, реализованный в IL коде
Стоит отметить, что алгоритм быстрого возведения в степень не является самым оптимальным алгоритмом возведения в степень. Например, ниже представлено перемножение одинаковых переменных пять раз двумя способами. Оптимизации типа x^4 + x^3 + x^2 + x = x*(x*(x*(x + 1) + 1) + 1) тоже у меня не реализованы.
- var t = a ^ 2; a*a*a*a*a*a = t ^ 2 * t — обычный «быстрый» алгоритм.
- a*a*a*a*a*a = (a ^ 3) ^ 2 — оптимальный «быстрый» алгоритм.
Кстати, еще стоит упомянуть, что для обычных фиксированных чисел double, результат перемножения для упомянутых выше перемножений в разном порядке, будет различный (т.е. (a ^ 2) ^ 2 * a ^ 2 != (a ^ 3) ^ 2). И из-за этого некоторые компиляторы не оптимизируют многие подобные выражения. По этому поводу есть интересные Q&A в stackoverlofw: Why doesn't GCC optimize a*a*a*a*a*a to (a*a*a)*(a*a*a)? и Why Math.Pow(x, 2) not optimized to x * x neither compiler nor JIT?.
Оптимизация локальных переменных
Как известно из предыдущих этапов, локальные переменные используются для хранения результата всех функций, которые встречаются в исходном выражении более 1 раза. Для работы с локальными переменными используются всего две простые инструкции: stloc и ldloc, которые используют один аргумент, отвечающий за номер данной локальной переменной. Но если номер локальной переменной инкрементировать каждый раз при появлении повторяющегося результата вычислений (для ее создания), то локальных переменных может быть очень много. Для нивелирования данной проблемы, был реализован алгоритм сжатия жизненных циклов локальных переменных, процесс которого можно наглядно увидеть на рисунке ниже. Как видим, вместо 5 локальных переменных в выражении можно использовать всего 3. Однако этот «жадный» алгоритм не является самым оптимальным перестановки, однако он вполне подходит к реализуемой задаче.
 |  |
Компиляция неопределенных функций и их производных
В разработанной библиотеке можно использовать не только простые функции от одного переменного вида f(x), но и другие, такие как f(x,a,b(x)), где a — неизвестная константа, а b(x) — неизвестная функция, передаваемая в виде делегата. Как известно, определение производной от любой функции выглядит следующим образом: b(x)' = (b(x + dx) — b(x)) / dx. И когда модуль компиляции встречает неопределенную функцию, он генерирует следующий код:
Код вычисления производной неопределенной функции (dx = 0.000001)Для численного вычисления производных, можно использовать и другие, более точные методы.
Тестирование
WolframAlpha
Загрузка и выгрузка сборок с помощью доменов
Создание домена, сборки из файла, создание экземпляра определенного типа и получение объектов с информацией о методах (MethodInfo):
Вычисление результата скомпилированной функции:
Выгрузка домена и удаление файла со сборкой:
Сравнение сгенерированного IL кода
Как видим, создалось большое количество локальных переменных для хранения уже рассчитанных результатов функций. Хотя в реальности локальных переменных меньше, потому что, например, для double arg_24_0 = 2.0; не создается локальная переменная, это просто константа.
Конечно, в реальных приложениях подобные выражения редко встречаются, но, тем не менее, описанные оптимизации могут использоваться в других, более прикладных случаях и для лучшего понимания работы компилятора.
Заключение
P.S. В сердечке спрятана длинная формула с учетом перестановки слагаемых, множителей и упрощения. Во время ее усложнения использовалась разработанная программа.
UPDATE: Так как никто не отгадал, что зашифровано в сердечке, то выкладываю результат. Данная формула является частным случаем многочлена Матиясевича, множество положительных значений которых при неотрицательных значениях переменных совпадает с множеством простых чисел. На википедии также есть информация.
Этот урок посвящен числовым типам и типу Boolean. Рассмотрены вопросы приведения типов, арифметические и логические операции, возможности класса Math и преобразование чисел в строку и обратно.
Исходный код примеров из этой статьи можете скачать из нашего github-репозитория.
Числовые типы
Приведение типов
При работе с числовыми типами данных довольно часто приходится сталкиваться с “расширением” и с “сужением” типа. Для начала рассмотрим несколько примеров:
При компиляции этого кода никаких ошибок не будет несмотря на то, что мы присваиваем переменную одного типа ( byte ) переменной другого типа ( short ) для целых чисел это делать можно без последствий, так как в данном случае происходит расширение типа. Переменная типа byte может принимать значения из диапазона от -128 до 127, а short из диапазона от -32 768 до 32 767, что значительно превышает ограничения для byte . Таким образом, при присваивании значения переменной типа byte , переменной типа short не происходит потери данных. В обратную сторону это сделать не получится, если вы напишите код, приведенный ниже, то компиляция будет прервана с ошибкой:
Для того, чтобы такая операция могла быть выполнена, необходимо использовать явное приведение, тем самым, мы как бы говорим компилятору, что в курсе того, что делаем. Для явного приведения необходимо тип, к которому приводится значение переменной, указать перед ней в круглых скобках. Перепишем наш второй пример с использованием явного приведения:
Но имейте ввиду, что такая операция, по своей сути, не является безопасной, так как в этом случае возможно переполнение, что приведет к получению результата, который скорее всего вы не ожидаете:
В результате на консоль будет выведено следующее:
Проверка переполнения
Если переполнение является критичным моментом для некоторого участка кода вашего приложения, то можете использовать проверку переполнения с помощью ключевого слова checked . Суть его работы заключается в том, что если в рамках контекста, обозначенного через checked происходит переполнение, то будет выброшено исключение OverflowException . Пример использования для одного оператора приведен ниже:
Если необходимо провести проверку для группы операторов, то используйте checked следующим образом:
Overflow is detected!
Для того, чтобы выполнять такого типа проверку для всех вычислений в вашем приложении необходимо активировать эту опцию на этапе компиляции. Если вы работаете в Visual Studio , то зайдите в свойства проекта, перейти на вкладку Build и нажмите на кнопку “ Advanced… ”. В результате откроется окно с настройками:
В нем можно поставить (или убрать) галочку в поле “ Check for arithmetic overflow/underflow ”. Если установить галочку, то все вычисления будут проверяться на переполнение. В таком случае можно отдельно создавать блоки кода, в которых данная проверка производиться не будет, для этого используйте оператор unchecked :
Класс System.Convert
Для приведения типов можно воспользоваться классом System . Convert , который содержит методы для приведения одного типа к другому. Подробная документация по его возможностям приведена в официальной документации .
Приведем несколько примеров его использования. Вариант, когда приведение типа не приводит к переполнению:
Вариант, когда приведение типа приводит к переполнению, в этом случае будет выброшено исключение:
Арифметические операции
Из перечисленных выше арифметических операций, обратите внимание на операции инкремента и декремента. При использовании постфиксного варианта, вначале происходит возврат значения переменной, а потом выполнение операции, для префиксного наоборот.
Класс Math
Класс Math предоставляет реализации распространенных математических функций. Полный список представлен в официальной документации . Ниже будут рассмотрены некоторые из функций класса Math .
Функции округления
Math.Ceiling
Возвращает наименьшее число, которое больше либо равно заданному:
Возвращает наибольшее число, которое меньше либо равно заданному:
Округляет число до ближайшего целого значения. Значение посередине округляется до ближайшего четного.
Тригонометрические функции
Разное
Возвращает число e в заданной степени:
Если функция вызывается с одним аргументом, то возвращается натуральный логарифм числа:
Если с двумя аргументами, то возвращается логарифм числа по заданному основанию:
Возвращает десятичный логарифм числа:
Возвращает логарифм по основанию 2 от числа:
Возвращает число, возведенное в заданную степень:
Возвращает абсолютное значение числа:
Возвращает наименьшее из переданных чисел:
Возвращает наибольшее из переданных чисел:
Возвращает знак числа. Если число положительное, то будет возвращено значение 1, если отрицательное, то -1.
Преобразование числа в строку
Для форматирования строкового представления числа с плавающей точкой используйте Format с соответствующим набором маркеров, пример:
Преобразование строки в число
Преобразовать строку в число можно либо с помощью методов класса Convert , либо с помощью методов классов, представляющих числа.
Класс Convert
Класс Convert предоставляет набор статических методов для преобразования в базовые типы данных и обратно. Поддерживается следующий набор типов: SByte , Byte , Int16 , Int32 , Int64 , UInt16 , UInt32 , UInt64 , Single , Double , Decimal , Boolean , Char , DateTime , String .
Приведем несколько примеров:
При работе с Convert может происходить:
- Успешное преобразование.
- Выброс исключения InvalidCastException , если запрашиваемое преобразование не может быть выполнено. Это может происходить при попытке преобразовать типы Boolean, Double, Decimal, Single, DateTime в Char и обратно, DateTime в не строковый тип и обратно.
- Выброс исключения FormatException , если преобразование завершается с ошибкой.
- Выброс исключения OverflowException , если происходит потеря данных при сужении типа (см. Приведение типов).
Класс Convert позволяет работать с разными системами счисления. Поддерживаются двоичное (2), восьмеричное (8), десятичное (10) и шестнадцатеричное (16) основание:
Методы числовых типов
Другим способом преобразования строки в число является использование методов Parse и TryParse , которые предоставляют числовые типы данных. Метод TryParse пытает преобразовать переданную в него строку в число, если это возможно, то полученное значение присваивается второму аргументу с ключевым словом out и возвращает значение true , в ином случае возвращает значение false .
В первом случае преобразование строки “123” в число будет выполнено успешно, во втором нет.
Преобразовать строку в число можно также с помощью метода Parse , если процесс пройдет успешно, то будет возвращено численное значение соответствующего типа, если нет, то будет выброшено исключение ArgumentNullException , ArgumentException , FormatException или OverflowException .
Тип данных Boolean
Экземпляр типа данных Boolean можно создать через объявление либо получить в результате логической операции.
Логические операторы
| Название | Обозначение | Пример |
| Логическое отрицание | ! | !a |
| Логическое И | & | a & b |
| Логическое исключающее ИЛИ | ^ | a ^ b |
| Логическое ИЛИ | | | a | b |
| Условный оператор логического И | && | a && b |
| Условный оператор логического ИЛИ | || | a || b |
Операторы &, ^, | всегда обрабатывают оба операнда в выражении, операторы && и || вычисляют правый только в случае, если это необходимо.
Математические функции (Visual Basic)
Visual Studio 2013
Методы класса Math предоставляют тригонометрические, логарифмические и других общих математические функции.
В следующей таблице перечислены методы класса Math . М ожно использовать их в программе Visual Basic.
Возвращает абсолютное значение числа.
Возвращает угол, косинус которого равен указанному числу.
Возвращает угол, синус которого равен указанному числу.
Возвращает угол, тангенс которого равен указанному числу.
Возвращает угол, тангенс которого равен отношению двух указанных чисел.
Возвращает полный продукт 2 32 разрядных чисел.
Возвращает наименьшее целое значение, которое меньше или равно указанному Decimal или Double.
Возвращает косинус указанного угла.
Возвращает гиперболический косинус указанного угла.
Возвращает частное 2 32 или 64 разрядного разрядных знаковых целых чисел, а также возвращает остаток в параметре вывода.
Возвращает e (основание натуральных логарифмов), возведенное в заданную степень.
Возвращает наибольшее целое число, которое меньше или равно числу указанного типа Decimal или Double.
Возвращает остаток от деления, результаты из указанного числа другим указанным количеством.
Возвращает естественный ( e) базового логарифм заданного числа или логарифм заданного числа в определенной базе.
Возвращает логарифм с основанием 10 указанного числа.
Возвращает большее 2 чисел.
Возвращает меньшее из двух чисел.
Возвращает указанное число, возведенное в указанную степень.
Возвращает значение Decimal или значение Double, округленное до разным значений или с указанным количеством цифр.
Возвращает значение типа Integer, показывающее знак числа.
Возвращает синус указанного угла.
Возвращает гиперболический синус указанного угла.
Возвращает квадратный корень из указанного числа.
Возвращает тангенс указанного угла.
Возвращает гиперболический тангенс указанного угла.
Вычисляет неотъемлемую часть номера, определенных в Decimal или Double.
Для использования этих функций без уточнения импортировать пространство имен Math в проект, добавив следующий код в начало файла источника:
В этом примере метод Abs класса Math используется для вычисления абсолютного значения числа.
Dim MyNumber1 As Double = Math.Abs(50.3)
Dim MyNumber2 As Double = Math.Abs(-50.3)
В этом примере метод Atan класса Math используется для вычисления значения числа пи.
Public Function GetPi() As Double
' Calculate the value of pi.
Return 4.0 * Math.Atan(1.0)
В этом примере метод Cos класса Math используется для возврата косинуса угла.
Public Function Sec(ByVal angle As Double) As Double
' Calculate the secant of angle, in radians.
Return 1.0 / Math.Cos(angle)
В этом примере метод Exp класса Math используется для возврата числа e, возведенного в степень.
Public Function Sinh(ByVal angle As Double) As Double
' Calculate hyperbolic sine of an angle, in radians.
Return (Math.Exp(angle) - Math.Exp(-angle)) / 2.0
В этом примере метод Log класса Math используется для возврата натурального логарифма числа.
Public Function Asinh(ByVal value As Double) As Double
' Calculate inverse hyperbolic sine, in radians.
Return Math.Log(value + Math.Sqrt(value * value + 1.0))
В этом примере метод Round класса Math используется для округления числа до ближайшего целого числа.
Dim MyVar2 As Double = Math.Round(2.8)
В этом примере метод Sign класса Math используется для определения знака числа.
Dim MySign1 As Integer = Math.Sign(12)
Dim MySign2 As Integer = Math.Sign(-2.4)
Dim MySign3 As Integer = Math.Sign(0)
В этом примере метод Sin класса Math используется для возврата синуса угла.
Public Function Csc(ByVal angle As Double) As Double
' Calculate cosecant of an angle, in radians.
Return 1.0 / Math.Sin(angle)
В этом примере метод Sqrt класса Math используется для вычисления квадратного корня числа.
Dim MySqr1 As Double = Math.Sqrt(4)
Dim MySqr2 As Double = Math.Sqrt(23)
Dim MySqr3 As Double = Math.Sqrt(0)
' Returns NaN (not a number).
Dim MySqr4 As Double = Math.Sqrt(-4)
В этом примере метод Tan класса Math используется для возврата тангенса угла.
Читайте также:


