Решение комбинаторных и вероятностных задач в ms excel
Компьютерная технология обучения представляет технологию обучения, основанную на принципах информатики и реализуемую с помощью компьютеров. Применение компьютера в качестве нового и динамичного развивающего средства обучения - главная отличительная особенность компьютерной технологии. Использование компьютера, а значит, программного обеспечения обучающего характера позволяет учителям - предметникам разнообразить и углубить учебный процесс, что благотворно сказывается на эффективности обучения.
В процессе широкой информатизации общества существенное значение приобретает использование информационных технологий в системе образования, развитие которых требует постоянного повышения квалификации учителей - предметников. Взаимосвязанное изучение информатики и математики позволяет познакомить школьников с элементами математической исследовательской деятельности и применить компьютер в качестве рабочего инструмента исследования. Такой подход в изучении способствует развитию творческой активности учащихся, дает возможность осуществить интеграцию учебной и организационной деятельности ученика и учителя, осуществить сочетание индивидуального подхода с различными формами коллективной учебной деятельности, учитывая уровневую дифференциацию.
Также, нельзя не отметить, что при обучении математике дидактические возможности новых информационных технологий можно реализовать более широко, чем при изучении других предметных областей. Одна из причин этого, на наш взгляд, заключается в том, что информационные технологии включают в себя математическую составляющую, максимально заметную для обучаемых именно при изучении математических дисциплин посредством компьютерной техники. Интегрированное обучение математики и информатики в старшей школе позволяет формировать у учащихся определенную систему знаний, умений и навыков; способствует достижению более высокого уровня умственного развития учащихся, развитию у них способности к самообучению. Считается рациональным проводить изучение многих математических тем с использованием информационных технологий. Наиболее наглядно это можно продемонстрировать
Отметим некоторые варианты использования ПК в учебной деятельности:
1 создание дидактического материала для урока;
2 наглядность изучаемого материала;
3 использование программного обеспечения непосредственно на уроке математики;
4 применение готового программного обеспечения по математике l .
Выгодные особенности работы с компьютерной поддержкой на уроке:
5 сокращается время при выработке технических навыков учащихся;
6 увеличивается количество тренировочных заданий;
7 достигается оптимальный темп работы ученика;
8 легко достигается уровневая дифференциация обучения;
9 учащийся становится субъектом обучения, ибо программа требует от него активного управления;
10 повышается мотивация учебной деятельности.
Отказываться от компьютера в обучении математики нельзя. Критерий полезности, на наш взгляд, можно сформулировать так: та или иная компьютерная технология целесообразна, если она позволяет получить такие результаты обучения, какие нельзя получить без применения этой технологии. Поэтому без компьютера работа будет перегружена массой дополнительных, рутинных построений, вычислений и простейших действий. И из-за обилия вспомогательных действий трудно сформировать и проконтролировать нужное умение.
Благодаря интеграции математики и информатики материал, который в настоящее время изучается в информатике, не является оторванным от жизни: учащиеся приобретают навыки применения тех или иных программных средств на практике. При внедрении информационных технологий в образование учебный материал предполагает наличие разветвлений, различных скоростей и способов его прохождения. Постоянно осуществляется контроль и поддерживается на необходимом уровне мотивация учения. Предполагается оказание помощи учащемуся в виде подсказок, пояснений и дополнительных указаний и задач. В условиях, когда математические способности у учащихся развиты не одинаково и разброс здесь очень велик, этот подход позволяет дать каждому учащемуся возможность работать в том темпе, при котором он наилучшим образом усваивает учебный материал. Таким образом, можно говорить о том, что интеграция информационных технологий в образование позволяет осуществлять индивидуальный подход к учащимся и тем самым помогает дифференциации образования, а интеграция информационных технологий в естественно-математические предметы в целом и в математику в частности дает возможность сделать учебный процесс наиболее эффективным как с точки зрения учителя, так и с точки зрения учащегося.
Таким образом, актуальность данного исследования определяется низким уровнем знаний учителей - предметников об использовании информационных технологий в качестве инструмента обучения.
Цель курсовой работы:
1. Формирование у учащихся знаний по информационным технологиям в математике, умения правильного выбора инструментария для решения практических задач.
Объектом исследования выступает процесс использования информационных технологий как инструмента обучения в курсе математики при изучении темы
Разработка методики решения математических задач с использованием Excel ;
Составление урока по теме “Элементы комбинаторики»
Разработка методов использования информационных технологий на примере темы «Элементы комбинаторики»
1. Краткая характеристика системы
В современном обществе использование информационных технологий становится необходимым практически в любой сфере деятельности человека. Овладение навыками этих технологий еще за школьной партой во многом определяет успешность будущей профессиональной подготовки нынешних учеников. Опыт показывает, что овладение этими навыками протекает гораздо эффективней, если происходит не только на уроках информатики, а находит свое продолжение и развитие на уроках учителей-предметников. Этот подход выдвигает новые требования к подготовке учителя-предметника, ставит перед ним новые проблемы, заставляет осваивать новую технику и создавать новые методики преподавания, основанные на использовании современной информационной среды обучения. Преподавание математики, в силу особенностей самого предмета, представляет собой наиболее благоприятную сферу для применения современных информационных технологий. Проводимая работа в этом направлении содержит как чисто демонстрационную составляющую, дающую ученикам расширенные представления о возможностях использования информационных технологий, так и составляющую, требующую активного применения учениками знаний, полученных на уроках информатики. В процессе преподавания математики, информационные технологии могут использоваться в различных формах. Одним из самых удачных является внедрение табличного процессора EXCEL.
Excel, пожалуй, самая популярная сегодня программа электронных таблиц. Она входит в офисный пакет MS Office. Ею пользуются деловые люди и ученые, бухгалтеры и журналисты. С ее помощью ведут разнообразные списки, каталоги и таблицы, составляют финансовые и статистические отчеты, обсчитывают данные опросов общественного мнения и состояние торгового предприятия, обрабатывают результаты научного эксперимента, ведут учет, готовят презентационные материалы.
Excel сумеет вычислить суммы по столбцам и строкам таблицы, взять проценты, подсчитать среднее арифметическое, банковский процент или дисперсию; в нем вообще можно использовать множество стандартных функций – финансовых, математических, логических, статистических.
Оформление таблиц может быть самым разнообразным, возможности форматирования данных – как в хорошем текст-процессоре: можно менять шрифты, начертания, выделять строки, столбцы или отдельные ячейки текста цветом, рамочками и линеечками, закрашивать области фоном или цветом, строить по табличным данным графики и диаграммы, вставлять в таблицу картинки и т.п.
Надо сказать, что программа достаточно мощная, возможности ее весьма обширны. Одних только математических, логических, бухгалтерских, статистических функций, которые Excel умеет выполнять над табличными данными – более 200 штук. Именно поэтому применение Excel в математике весьма эффективно и дает большие возможности учителю предметнику. В процессе преподавания математики Excel может использоваться в изучении многих тем:
Перестановкой множества из n элементов называется расположение элементов в определенном порядке.
Элементами множества могут быть числа, буквы и вообще любые объекты. Главное, чтобы эти элементы были различными. Т.к. любому объекту можно сопоставить число, то для Перестановок обычно используют конечное множество целых чисел, например, . Хотя множества из букв также можно часто встретить в литературе. Например, все различные Перестановки множества из трех элементов – это abc , acb , bac , bca , cab , cba .
Число Перестановок n элементов равно n! (факториал).

Для вычисления факториала в MS EXCEL есть функция =ФАКТР() , английский вариант FACT(). Понятно, что число перестановок растет очень быстро с ростом n: для n=7 число перестановок равно 5040. Справедливости ради, нужно отметить, что зачастую сами варианты перестановок находить не требуется, главное – найти их количество.
Примечание : Перестановки можно считать частным случаем размещений при n=k (см. статью Размещения без повторений: Комбинаторика в MS EXCEL ). Поэтому для вычисления количества перестановок можно использовать функцию ПЕРЕСТ() . Для n=7 число Перестановок вычисляется по формуле =ПЕРЕСТ(7;7)
Примечание : О Перестановках с повторениями (с возвращением элементов обратно во множество, из которого они берутся, после выборки каждого элемента) можно прочитать в статье Перестановки с повторениями: Комбинаторика в MS EXCEL .
В файле примера создана универсальная формула для вывода всех Перестановок для заданного n. Например, для n=3.

Задача
6 машин разных марок участвуют в гонках на выживание: LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo. Определить число возможных вариантов распределения мест между всеми участниками.
Нам нужно определить число перестановок 6 машин на 6-и местах. Т.е. n=6. Оказывается, что таких перестановок 720: =ПЕРЕСТ(6;6) или 6! =ФАКТР(6)
Воспользуемся файлом примера , чтобы найти все варианты перестановок.
Произвольным образом сопоставим маркам машин числовые значения и сделаем сокращения названий марок: LADA Granta (LG=1), Hyundai Solaris (HS=2), …

Введя в ячейке В5 значение 6, определим все варианты расстановок машин на занятых ими в гонке местах.

Примечание : О Размещениях можно прочитать в статье Размещения без повторений: Комбинаторика в MS EXCEL , а о Сочетаниях в статье Сочетания без повторений: Комбинаторика в MS EXCEL .
Инверсии перестановок
Для каждой перестановки a 1, a 2, a 3. a n из n целых чисел 1, 2, 3, . n , инверсией называется пара ( a i, a j) если для i a j. Число инверсией в перестановке показывает насколько перестановка является "несортированной" по возрастанию.
Например, число инверсий в перестановке 1, 2, 3, 4 равно 0 (перестановка из 4-х целых чисел отсортирована по возрастанию от 1 до 4), а число инверсий в перестановке 4, 3, 1, 2 равно 5, т.к.:
- первый элемент (i=1) равен 4 и он больше 3-х чисел (с j=2, 3, 4), которые расположены правее (4>3, 4>1, 4>2), т.е. мы имеем 3 инверсии;
- второй элемент (i=2) равен 3 и он больше 2-х чисел (с j=3, 4), которые расположены правее (3>1, 3>2), т.е. мы имеем еще 2 инверсии;
- так третий элемент (i=3) равен 1 и он меньше числа с j=4, которое расположено правее (1 файле примера для каждой Перестановки подсчитывается число инверсией.

Инверсии перестановок, например, используются при вычислении определителя матрицы (см. статью Вычисление определителя матрицы в MS EXCEL ).
Давайте разберем на примерах основные формулы комбинаторики: сочетания, размещения, перестановки без повторений и научимся вычислять их с помощью встроенных функций Excel.
Ниже вы найдете для каждой формулы инструкции по вычислению в эксель, пример задачи, ссылку на калькулятор и видеоурок и шаблон Excel. Удачи в изучении!
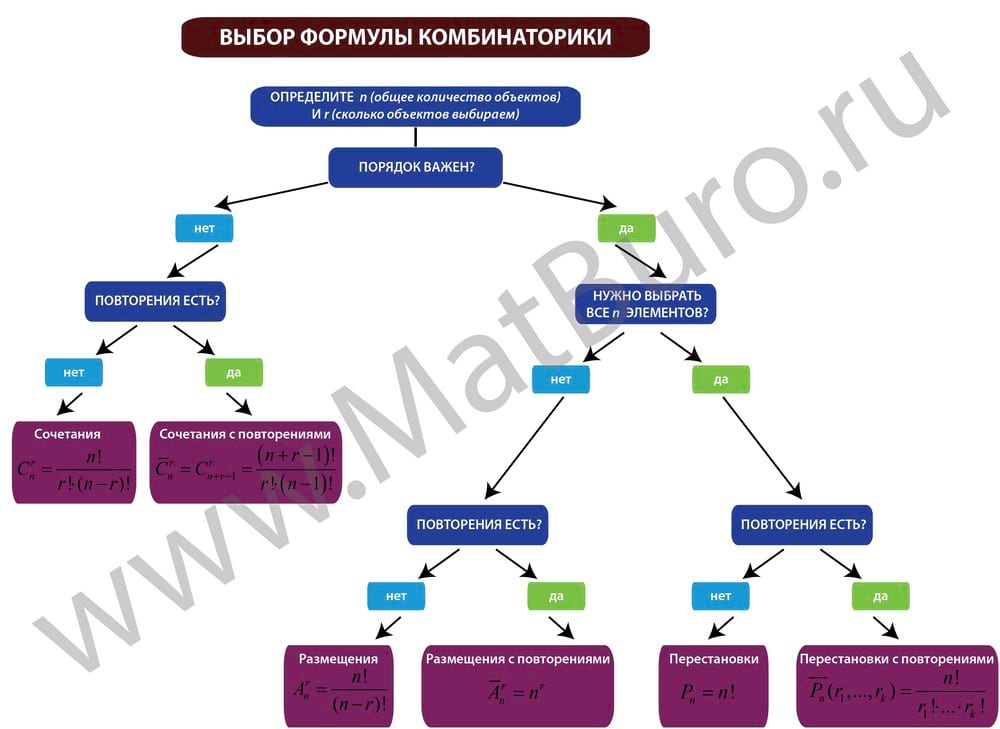
Как выбрать формулу комбинаторики?
Нужно последовательно (см. схему выше) ответить на несколько вопросов:
- Сколько у нас есть объектов (число $n$)?
- Важен ли их порядок в комбинации?
- Могут ли встречаться повторяющиеся элементы?
- Нужно выбрать все элементы или только $k\lt n$?
Отвечая на эти вопросы, двигаемся по стрелкам схемы и получаем название формулы комбинаторики:
Перестановки в Excel
Пусть имеется $n$ различных объектов. Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно
$$P_n=n!=1\cdot 2\cdot 3 \cdot . \cdot (n-1) \cdot n$$
Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.
Для нахождения числа перестановок в Excel можно использовать одну из двух функций:
=ПЕРЕСТ($n$;$n$) или =ФАКТР($n$) , где $n$ - число переставляемых объектов.
Задача. Сколькими способами можно расставить 10 различных книг на одной полке?
Вводим число объектов 10 и получаем ответ: 3628800 способов.

В режиме формул это выглядит так:

Перестановки с повторениями в Excel
Пусть имеется $n$ объектов различных типов: $n_1$ объектов первого типа, $n_2$ объектов второго типа. $n_k$ объектов $k$-го типа. Сколькими способами можно переставить все объекты между собой?
Будем переставлять $n$ объектов всеми возможными способами (их будет $n!$). Но так как некоторые объекты совпадают, итоговое число будет меньше. В частности, $n_1$ объектов первого типа можно переставлять между собой $n_1!$ способами, но они не меняют итоговую перестановку. Аналогично для всех остальных объектов, поэтому число перестановок с повторениями есть
Для нахождения числа перестановок в Excel будем использовать функцию =ФАКТР() , которая находит факториал чисел и обычные действия ( умножение, деление ).
Задача. Сколько различных слов можно составить из букв слова "колокол"?
Вводим число букв $n=7$, а также $n_1=2$ (2 буквы "к"), $n_2=3$ (3 буквы "о"), $n_3=2$ (2 буквы "л"), и получаем ответ: 210 слов.

В режиме формул это выглядит так:

Размещения в Excel
Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из $n$ объектов по $k$, а их число равно
Для нахождения числа размещений в Excel используем функцию =ПЕРЕСТ($n$;$k$) .
Задача. В группе учится 10 студентов. Нужно выбрать из них 3 человек на должности старосты, заместителя и дежурного. Сколькими способами можно это сделать?
Вводим $n=10$, $k=3$ и получаем ответ: 720 способов.

В режиме формул это выглядит так:

Размещения с повторениями в Excel
Число размещений с повторениями из $n$ объектов по $k$ можно найти по формуле
Для вычисления в Excel используем функцию =СТЕПЕНЬ($n$;$k$) .
Задача. Сколько трехзначных номеров можно составить для автомобилей, используя все возможные цифры от 0 до 9?
Вводим $n=10$ (количество возможных цифр), $k=3$ (количество цифр в номере) и получаем ответ: 1000 номеров.

В режиме формул это выглядит так:

Сочетания в Excel
Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из $n$ объектов по $k$, а их число равно
Для нахождения числа сочетаний в Excel используем функцию =ЧИСЛКОМБ($n$;$k$) .
Задача. В поход пошло 10 учеников. Нужно выбрать из них 3, которые понесут флажки. Сколькими способами можно это сделать?
Вводим $n=10$, $k=3$ и получаем ответ: 120 способов.

В режиме формул это выглядит так:

Сочетания с повторениями в Excel
Количество сочетаний с повторениями из $n$ объектов по $k$ можно найти по формуле
Для вычисления в Excel используем функцию =ЧИСЛКОМБ($n+k-1$;$k$) .
Задача. В магазине продаются мячики трех цветов: желтые, красные и синие. Родительский комитет собирается купить 10 мячиков. Сколько возможных вариантов выбора у них есть?
Вводим $n=3$ (вида объектов), $k=10$ (нужно выбрать) и получаем ответ: 66 способов.
Комбинаторика — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения элементов) и отношения на них. Термин комбинаторика был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве». Excel поддерживает ряд функций комбинаторики. Чтобы разобраться, какую формулу использовать, следует ответить на ряд вопросов:
- Исходное множество содержит только уникальные элементы, или некоторые из них могут повторяться?
- Операция выполняется со всеми элементами множества, или только с некоторой выборкой из них?
- Важен ли порядок элементов в выборке?
- После выбора элемента мы его возвращаем назад?
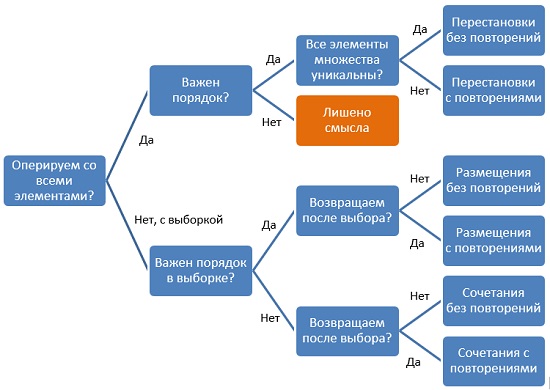
Рис. 1. Дерево решений, какую формулу комбинаторики использовать
Перестановки без повторений
Возьмем несколько различных элементов (предметов) и будем переставлять их всевозможными способами, оставляя неизменным их число и меняя только их порядок (рис. 2). Каждая из получившихся таким образом комбинаций носит название перестановки. Перестановкой из n элементов называется упорядоченное множество, составленное из всех элементов множества.
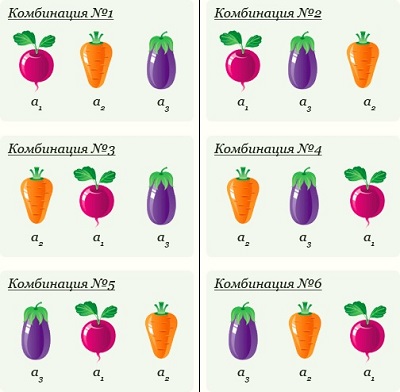
Рис. 2. Перестановки (картинка взята здесь)
Если все n элементы разные, то число перестановок обозначается Pn от perturbation.
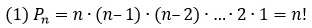
С другой стороны, произведение n первых натуральных чисел называется n-факториал и обозначается n!
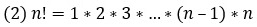
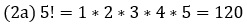
По определению: 1! = 1; 0! = 1.
Функция в Excel =ФАКТР(n). Факториал растет очень быстро. Существенно быстрее экспоненты (рис. 3).
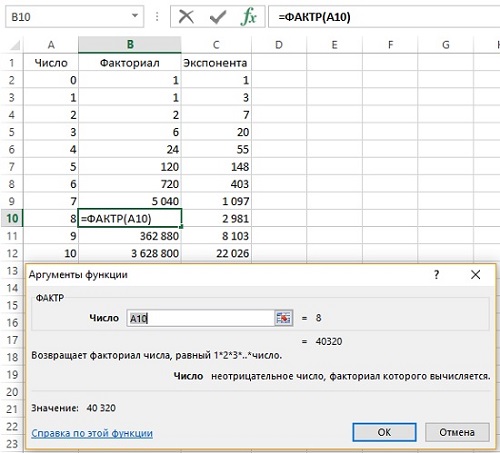
Рис. 3. Расчет числа перестановок без повторений с помощью факториала
Перестановки с повторениями
Если в основном n множестве не все элементы разные, то число перестановок будет меньше n! Например, если наше множество состоит из трех яблок и одной груши, то всего возможно 4 перестановки (рис. 4). Груша может быть первой, второй, третьей или четвертой, а яблоки неразличимы).

Рис. 4. Перестановки с повторениями (картинка найдена здесь)
В общем случае, можно сказать: последовательность длины n, составленная из k разных символов, первый из которых повторяется n1 раз, второй – n2 раз, третий – n3 раз, …, k-й – nk раз (где n1 + n2 + … + nk = n) называется перестановкой с повторениями из n элементов.
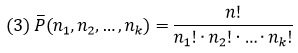
Пример. Сколько различных пятибуквенных слов можно составить из букв слова «манна»?
Решение. Буквы а и н повторяются 2 раза, а буква м один раз.
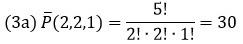
Размещение без повторений
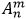
Размещением из n элементов по m называется упорядоченный набор из m различных элементов, выбранных из n-элементного множества (все элементы множества уникальны; позиции элементов в выборке важны). Число размещений обозначается от arrangement.
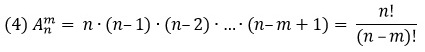
Например, два элемента из трех можно выбрать и расположить шестью способами (рис. 4):

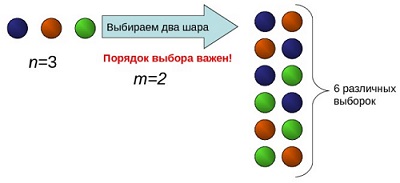
Рис. 5. Размещение без повторений (картинка из презентации)
Если m = n количество элементов совпадает с количеством имеющихся мест для размещения. Знаменатель в формуле (4) превращается в 0! = 1. Остается только числитель n! А это – изученная выше перестановка без повторений; см. формулу (1).
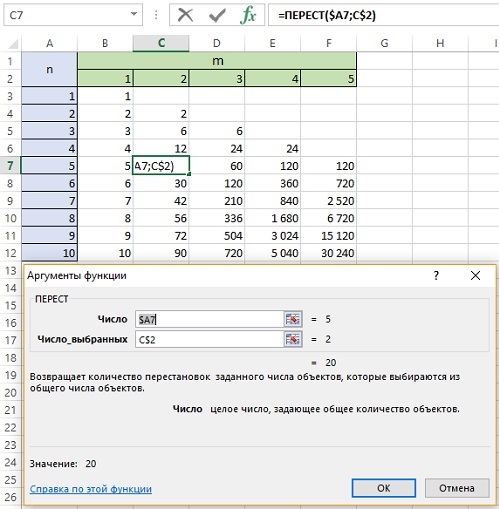
Рис. 6. Размещение без повторений; обратите внимание на смешанные ссылки, которые позволяют протянуть формулу на всю таблицу
Размещение с повторениями
Размещение с повторениями по смыслу отличается от перестановок с повторением. Перестановки с повторением – это операция над множеством, которое состоит из нескольких видов элементов, так что каждый вид представлен несколькими одинаковыми элементами. Размещение с повторениями – выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором.
Например, если у вас множество, включающее грушу, яблоко и лимон, и вам нужно выбрать два элемента, так что после первого выбора вы возвращаете выбранный предмет назад, то существует девять различных комбинаций (рис. 7).

Рис. 7. Размещение с повторениями
В общем случае размещение с повторениями или выборка с возвращением – это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз. По правилу умножения количество размещений с повторениями из n по k:

В Excel используется функция ПЕРЕСТА(n;k).
Задача. Сколько различных номеров можно составить в одном коде региона?
Подсказка. В номере используется 12 букв алфавита, также существующих и в латинском алфавите (А, В, Е, К, М, Н, О, Р, С, Т, У, Х).
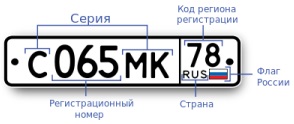
Решение. Можно воспользоваться формулой для размещения с повторениями:

Каждую цифру можно выбрать 10 способами, а всего цифр 3, при этом они могут повторяться, и их порядок важен. Каждую букву можно выбрать 12 способами, при этом буквы могут повторяться, и их порядок важен.
Сочетания без повторений
Сочетаниями из n множества по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом (в сочетаниях не учитывается порядок элементов).
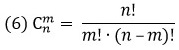
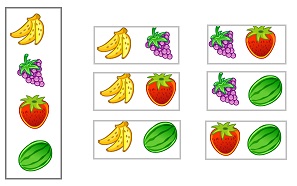
Например, два элемента из 4 сочетаются 6 способами (порядок следования не важен):

Сочетания без повторений образуют знаменитый треугольник Паскаля (рис. 10). В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Числа в строках, составляющие треугольник Паскаля, являются сочетаниями

где n – номер строки, m – номер элемента в строке, начиная с нулевого. Например, в строке 7:

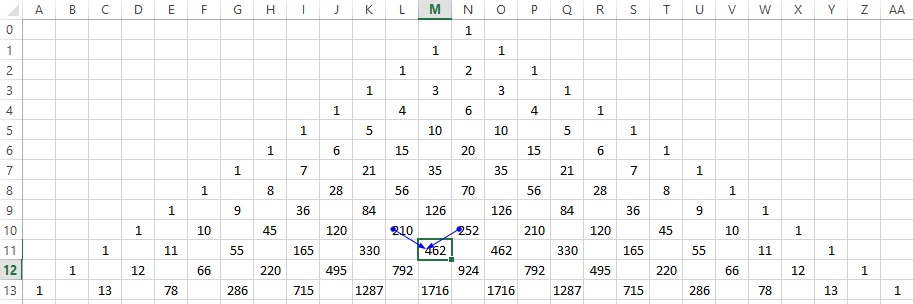
Рис. 10. Треугольник Паскаля; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
В Excel используется функция =ЧИСЛКОМБ(n;m).
Сочетания с повторениями
Сочетания с повторениями по смыслу похожи на размещение с повторениями – это выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором. При этом порядок в выборке не важен.
Например, два предмета из четырех можно выбрать 10 способами, если после каждого выбора предмет возвращается назад (рис. 11).

В общем случае, число сочетаний с повторениями:

Для нашего примера с фруктами
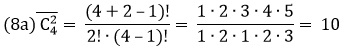
В Excel для подсчета числа сочетаний с повторениями используется функция =ЧИСЛКОМБА(n;m). В нашем примере =ЧИСЛКОМБА(4;2) = 10.
1 комментарий для “Комбинаторика в Excel”
Спасибо большое за понятное и наглядное изложение этой сложной темы! Не в первый раз Ваши публикации выручают меня, это просто энциклопедия полезнейшего контента!
Читайте также:


