Ниже на четырех языках программирования записана программа которая вводит натуральное число x
№1. Ниже записана программа. Получив на вход число x , эта программа печатает два числа, L и M. Укажите наибольшее из таких чисел x, при вводе которых алгоритм печатает сначала 3, а потом 7.
var x, L, M: integer;
while x > 0 do begin
if x mod 2 = 0 then
M:= M + (x mod 10) div 2;
writeln(L); write(M);
Рассмотрим цикл, число шагов которого зависит от изменения переменной x:
while x > 0 do begin
Т. к. оператор div оставляет только целую часть от деления, то при делении на 10 это равносильно отсечению последней цифры.
Из приведенного цикла видно, что на каждом шаге от десятичной записи x отсекается последняя цифра до тех пор, пока все цифры не будут отсечены, то есть x не станет равно 0; поэтому цикл выполняется столько раз, сколько цифр в десятичной записи введенного числа, при этом число L столько же раз увеличивается на 1. Следовательно, конечное значение L совпадает с числом цифр в x. Для того, чтобы L стало L=3, x должно быть трёхзначным.
Теперь рассмотрим оператор изменения M:
if x mod 2 = 0 then
M:= M + (x mod 10) div 2;
Оператор mod оставляет только остаток от деления, при делении на 10 это последняя цифра x.
Условие x mod 2 = 0 означает следующее: чтобы M увеличилось, число x должно быть чётным.
Предположим, исходное x нечётное, тогда на первом шаге M = 0.
Если на втором шаге x также нечётное (вторая цифра исходного числа нечётная), то M = 0, причём каким бы ни было значение x на третьем шаге, мы не сможем получить M = 7, поскольку остаток от деления чётного числа на 10 не превосходит 8, а 8 / 2 = 4, следовательно, вторая цифра исходного x чётная.
Тогда первая цифра может принимать значения 2, 4, 6, 8, но мы ищем наибольшее x, поэтому сделаем первую цифру, равной 9, тогда наше предположение не удовлетворяет условию задачи, и последняя цифра исходного числа обязана быть чётной, т.е. исходное x чётно.
7 = 4 + 3, чему соответствуют цифры 8 и 6. Теперь, располагая цифры по убыванию, находим наибольшее возможное x: x = 986.
№2. Ниже на пяти языках программирования записан алгоритм. Получив на вход число x, этот алгоритм печатает числа: a и b. Укажите наибольшее четырехзначное число x, при вводе которого алгоритм печатает сначала 5, а потом 7.
1)На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о длине этих дорог в километрах. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Известно, что длина дороги ЕЖ больше, чем длина дороги БВ. Определите длину дороги АД. В ответе запишите целое число – длину дороги в километрах.
Правильный ответ: 7
3)Даны фрагменты двух таблиц из базы данных. Каждая строка таблицы 2 содержит информацию о ребёнке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке таблицы 1. На основании имеющихся данных определите количество людей, у которых есть родной или двоюродный брат, разница в возрасте с которым составляет не более двух лет.
Правильный ответ: 6
Правильный ответ: 101101
5)Алгоритм получает на вход натуральное число N > 1 и строит по нему новое число R следующим образом: 1. Строится двоичная запись числа N. 2. Подсчитывается количество нулей и единиц в полученной записи. Если их количество одинаково, в конец записи добавляется её последняя цифра. В противном случае в конец записи добавляется та цифра, которая встречается реже. 3. Шаг 2 повторяется ещё два раза. 4. Результат переводится в десятичную систему счисления. Пример. Дано число N = 19. Алгоритм работает следующим образом: 1. Двоичная запись числа N: 10011. 2. В полученной записи нулей меньше, чем единиц, в конец записи добавляется 0. Новая запись: 100110. 3. В текущей записи нулей и единиц поровну, в конец записывается последняя цифра, это 0. Получается 1001100. В этой записи единиц меньше, в конец добавляется 1: 10011001. 4. Результат работы алгоритма R = 153. При каком наименьшем исходном числе N > 99 в результате работы алгоритма получится число, кратное 4?
Правильный ответ: 103
6)Определите, при каком наименьшем введённом значении переменной s программа выведет число 11. Для Вашего удобства программа представлена на четырёх языках программирования.
Правильный ответ: 191
7)В информационной системе хранятся изображения размером 1024 × 768 пикселей. Методы сжатия изображений не используются. Каждое изображение дополняется служебной информацией, которая занимает 1280 Кбайт. Для хранения 2048 изображений потребовалось 4 Гбайт. Сколько цветов использовано в палитре каждого изображения?
Правильный ответ: 256
8)Вероника составляет 3-буквенные коды из букв В, Е, Р, О, Н, И, К, А, причём буква В должна входить в код ровно один раз. Все полученные коды Вероника записала в алфавитном порядке и пронумеровала. Начало списка выглядит так: 1. ААВ 2. АВА 3. АВЕ … На каком месте будет записан первый код, не содержащий ни одной буквы А?
Правильный ответ: 23
9)Электронная таблица содержит результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите, сколько раз за время измерений результат очередного измерения оказывался выше результата предыдущего на 2 и более градусов.
Правильный ответ: 440
10)Определите, сколько раз в тексте произведения А.С. Пушкина «Дубровский» встречается существительное «ключ» в любом числе и падеже.
Правильный ответ: 6
Правильный ответ: 2700
13)На рисунке представлена схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И, К, Л, М, Н, П, Р, С. По каждой дороге можно передвигаться только в направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт С, проходящих через пункт Ж?
Правильный ответ: 169
14)Значение выражения 7297 + 316 – 18 записали в системе счисления с основанием 9. Сколько раз в этой записи встречается цифра 0?
15)Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа A формула ДЕЛ(A, 45) /\ (ДЕЛ(750, x) → (¬ДЕЛ(A, x) → ¬ДЕЛ(120, x))) тождественно истинна, то есть принимает значение 1 при любом натуральном x?
16)Обозначим через mod(a, b) остаток от деления натурального числа a на натуральное число b. Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями: F(0) = 0; F(n) = F(n/3), если n > 0 и при этом mod(n, 3) = 0; F(n) = mod(n, 3) + F(n – mod(n, 3)), если mod(n, 3) > 0. Назовите минимальное значение n, для которого F(n) = 11.
17)Назовём натуральное число подходящим, если у него ровно 3 различных простых делителя. Например, число 180 подходящее (его простые делители – 2, 3 и 5), а число 12 – нет (у него только два различных простых делителя). Определите количество подходящих чисел, принадлежащих отрезку [10 001; 50 000], а также наименьшее из таких чисел. В ответе запишите два целых числа: сначала количество, затем наименьшее число.
18)Дан квадрат 15 × 15 клеток, в каждой клетке которого записано целое число. В левом верхнем углу квадрата стоит робот. За один ход робот может переместиться на одну клетку вправо, вниз или по диагонали вправо вниз. Выходить за пределы квадрата робот не может. Необходимо переместить робота в правый нижний угол так, чтобы сумма чисел в клетках, через которые прошёл робот (включая начальную и конечную), была максимальной. В ответе запишите максимально возможную сумму. Исходные данные записаны в электронной таблице. Пример входных данных (для таблицы размером 4 × 4):Для указанных входных данных ответом будет число 95 (робот проходит через клетки с числами 4, 37, 24, 9, 21).
19)Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 5 камней, а в другой 9 камней; такую позицию мы будем обозначать (5, 9). За один ход из позиции (5, 9) можно получить любую из четырёх позиций: (6, 9), (10, 9), (5, 10), (5, 18). Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 77. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 77 или больше камней. В начальный момент в первой куче было 8 камней, во второй куче – S камней, 1 ≤ S ≤ 68. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Назовите минимальное значение S, при котором это возможно.
20)Для игры, описанной в задании 19, найдите все такие значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания.
21)Для игры, описанной в задании 19, укажите максимальное значение S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть при любой игре Пети.
22)Ниже на четырёх языках программирования записана программа, которая вводит натуральное число x, выполняет преобразования, а затем выводит два числа. Укажите наименьшее возможное значение x, при вводе которого программа выведет числа 3 и 10.
23)Исполнитель преобразует число на экране. У исполнителя есть три команды, которым присвоены номера: 1. Прибавить 1 2. Умножить на 2 3. Умножить на 3 Первая команда увеличивает число на экране на 1, вторая умножает его на 2, третья – умножает на 3. Программа для исполнителя – это последовательность команд. Сколько существует программ, которые преобразуют исходное число 2 в число 36, и при этом траектория вычислений содержит число 12 и не содержит числа 30? Траектория вычислений – это последовательность результатов выполнения всех команд программы. Например, для программы 213 при исходном числе 4 траектория будет состоять из чисел 8, 9, 27.
24)Текстовый файл содержит строки различной длины. Общий объём файла не превышает 1 Мбайт. Строки содержат только заглавные буквы латинского алфавита (ABC…Z). Необходимо найти строку, содержащую наименьшее количество букв G (если таких строк несколько, надо взять ту, которая находится в файле раньше), и определить, какая буква встречается в этой строке чаще всего. Если таких букв несколько, надо взять ту, которая позже стоит в алфавите. Пример. Исходный файл: GIGA GABLAB AGAAA В этом примере в первой строке две буквы G, во второй и третьей – по одной. Берём вторую строку, т. к. она находится в файле раньше. В этой строке чаще других встречаются буквы A и B (по два раза), выбираем букву B, т. к. она позже стоит в алфавите. В ответе для этого примера надо записать B.
25)Найдите все натуральные числа, принадлежащие отрезку [35 000 000; 40 000 000], у которых ровно пять различных нечётных делителей (количество чётных делителей может быть любым). В ответе перечислите найденные числа в порядке возрастания.
27)В текстовом файле записан набор натуральных чисел, не превышающих 108 . Гарантируется, что все числа различны. Из набора нужно выбрать три числа, сумма которых делится на 3. Какую наибольшую сумму можно при этом получить?
Сложные задания и ответы с варианта ИН2010402:
1)На рисунке схема дорог изображена в виде графа, в таблице содержатся сведения о длине этих дорог в километрах. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Известно, что длина дороги ЕЖ меньше, чем длина дороги БВ. Определите длину дороги ГИ. В ответе запишите целое число – длину дороги в километрах.
Правильный ответ: 20
3)Даны фрагменты двух таблиц из базы данных. Каждая строка таблицы 2 содержит информацию о ребёнке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке таблицы 1. На основании имеющихся данных определите количество людей, у которых есть родная или двоюродная сестра, разница в возрасте с которой составляет не более двух лет.
Правильный ответ: 1
Правильный ответ: 1011010
5)Алгоритм получает на вход натуральное число N > 1 и строит по нему новое число R следующим образом: 1. Строится двоичная запись числа N. 2. Подсчитывается количество нулей и единиц в полученной записи. Если их количество одинаково, в конец записи добавляется её последняя цифра. В противном случае в конец записи добавляется та цифра, которая встречается реже. 3. Шаг 2 повторяется ещё два раза. 4. Результат переводится в десятичную систему счисления. Пример. Дано число N = 19. Алгоритм работает следующим образом: 1. Двоичная запись числа N: 10011. 2. В полученной записи нулей меньше, чем единиц, в конец записи добавляется 0. Новая запись: 100110. 3. В текущей записи нулей и единиц поровну, в конец записывается последняя цифра, это 0. Получается 1001100. В этой записи единиц меньше, в конец добавляется 1: 10011001. 4. Результат работы алгоритма R = 153. При каком наименьшем исходном числе N > 104 в результате работы алгоритма получится число, кратное 4?
Правильный ответ: 107
6)Определите, при каком наименьшем введённом значении переменной s программа выведет число 13. Для Вашего удобства программа представлена на четырёх языках программирования.
Правильный ответ: 186
7)В информационной системе хранятся изображения размером 1024 × 768 пикселей. Методы сжатия изображений не используются. Каждое изображение дополняется служебной информацией, которая занимает 640 Кбайт. Для хранения 2048 изображений потребовалось 2 Гбайт. Сколько цветов использовано в палитре каждого изображения?
Правильный ответ: 16
8)Валерия составляет 3-буквенные коды из букв В, А, Л, Е, Р, И, Я, причём буква В должна входить в код ровно один раз. Все полученные коды Валерия записала в алфавитном порядке и пронумеровала. Начало списка выглядит так: 1. ААВ 2. АВА 3. АВЕ … На каком месте будет записан первый код, не содержащий ни одной буквы А?
Правильный ответ: 20
9)Электронная таблица содержит результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите, сколько раз за время измерений результат очередного измерения оказывался ниже результата предыдущего на 2 и более градусов.
Правильный ответ: 458
10)Определите, сколько раз в тексте произведения А.С. Пушкина «Дубровский» встречается существительное «пир» в любом числе и падеже.
Правильный ответ: 1
Правильный ответ: 3200
13)На рисунке представлена схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И, К, Л, М, Н, П, Р, С. По каждой дороге можно передвигаться только в направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт С, проходящих через пункт Л?
14)Значение выражения 7296 + 314 – 36 записали в системе счисления с основанием 9. Сколько раз в этой записи встречается цифра 0?
15)Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа A формула ДЕЛ(A, 40) /\ (ДЕЛ(780, x) → (¬ДЕЛ(A, x) → ¬ДЕЛ(180, x))) тождественно истинна, то есть принимает значение 1 при любом натуральном x?
16)Обозначим через mod(a, b) остаток от деления натурального числа a на натуральное число b. Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями: F(0) = 0; F(n) = F(n/3), если n > 0 и при этом mod(n, 3) = 0; F(n) = mod(n, 3) + F(n – mod(n, 3)), если mod(n, 3) > 0. Назовите минимальное значение n, для которого F(n) = 9.
17)Назовём натуральное число подходящим, если у него ровно 3 различных простых делителя. Например, число 180 подходящее (его простые делители – 2, 3 и 5), а число 12 – нет (у него только два различных простых делителя). Определите количество подходящих чисел, принадлежащих отрезку [50 001; 90 000], а также наименьшее из таких чисел. В ответе запишите два целых числа: сначала количество, затем наименьшее число.
19)Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Например, пусть в одной куче 5 камней, а в другой 9 камней; такую позицию мы будем обозначать (5, 9). За один ход из позиции (5, 9) можно получить любую из четырёх позиций: (6, 9), (10, 9), (5, 10), (5, 18). Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 93. Победителем считается игрок, сделавший последний ход, то есть первым получивший позицию, в которой в кучах будет 93 или больше камней. В начальный момент в первой куче было 12 камней, во второй куче – S камней, 1 ≤ S ≤ 80. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Назовите минимальное значение S, при котором это возможно.
20)Для игры, описанной в задании 19, найдите все такие значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания.
21)Для игры, описанной в задании 19, укажите максимальное значение S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть при любой игре Пети.
22)Ниже на четырёх языках программирования записана программа, которая вводит натуральное число x, выполняет преобразования, а затем выводит два числа. Укажите наименьшее возможное значение x, при вводе которого программа выведет числа 3 и 11.
23)Исполнитель преобразует число на экране. У исполнителя есть три команды, которым присвоены номера: 1. Прибавить 1 2. Умножить на 2 3. Умножить на 3 Первая команда увеличивает число на экране на 1, вторая умножает его на 2, третья – умножает на 3. Программа для исполнителя – это последовательность команд. Сколько существует программ, которые преобразуют исходное число 2 в число 39, и при этом траектория вычислений содержит число 13 и не содержит числа 30? Траектория вычислений – это последовательность результатов выполнения всех команд программы. Например, для программы 213 при исходном числе 4 траектория будет состоять из чисел 8, 9, 27.
24)Текстовый файл содержит строки различной длины. Общий объём файла не превышает 1 Мбайт. Строки содержат только заглавные буквы латинского алфавита (ABC…Z). Необходимо найти строку, содержащую наименьшее количество букв N (если таких строк несколько, надо взять ту, которая находится в файле раньше), и определить, какая буква встречается в этой строке чаще всего. Если таких букв несколько, надо взять ту, которая позже стоит в алфавите. Пример. Исходный файл: NINA NABLAB ANAAA В этом примере в первой строке две буквы N, во второй и третьей – по одной. Берём вторую строку, т. к. она находится в файле раньше. В этой строке чаще других встречаются буквы A и B (по два раза), выбираем букву B, т. к. она позже стоит в алфавите. В ответе для этого примера надо записать B.
25)Найдите все натуральные числа, принадлежащие отрезку [45 000 000; 50 000 000], у которых ровно пять различных нечётных делителей (количество чётных делителей может быть любым). В ответе перечислите найденные числа в порядке возрастания.
Ответы и задания для вариантов ИН2010201, ИН2010202 тренировочной работы №2 статград по информатике 11 класс для подготовки к ЕГЭ 2021, официальная дата проведения работы статград: 10.12.2020 (10 декабря 2020 год).
Ссылка для скачивания вариантов (ИН2010201-ИН2010202): скачать в PDF
Тренировочная работа №2 по информатике 11 класс статград 2020-2021 решать онлайн:
Сложные задания с варианта ИН2010201:
1)На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Выпишите последовательно, без пробелов и знаков препинания указанные на графе буквенные обозначения пунктов от П1 до П7: сначала букву, соответствующую П1, затем букву, соответствующую П2, и т. д.
Ответ: БДЖГВАЕ
3)Даны фрагменты двух таблиц из базы данных. Каждая строка таблицы 2 содержит информацию о ребёнке и об одном из его родителей. Информация представлена значением поля ID в соответствующей строке таблицы 1. На основании имеющихся данных определите количество людей, у которых в момент достижения 50 полных лет было не меньше двух внуков и внучек.
Ответ: 3
Ответ: 20
6)Определите, при каком наименьшем введённом значении переменной s программа выведет число 60. Для Вашего удобства программа представлена на четырёх языках программирования.
Ответ: 8
7)Для хранения в информационной системе документы сканируются с разрешением 300 dpi и цветовой системой, содержащей 216 = 65 536 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 9 Мбайт. В целях экономии было решено перейти на разрешение 200 dpi и цветовую систему, содержащую 256 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
Ответ: 2
8)Тимофей составляет 5-буквенные коды из букв Т, И, М, О, Ф, Е, Й. Буква Й может использоваться в коде не более одного раза, при этом она не может стоять на первом месте, на последнем месте и рядом с буквой И. Все остальные буквы могут встречаться произвольное количество раз или не встречаться совсем. Сколько различных кодов может составить Тимофей?
Ответ: 10476
9)Электронная таблица содержит результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите, сколько раз за время наблюдений температура в 8:00 была выше среднесуточной температуры того же дня.
Ответ: 30
10)Определите, сколько раз в тексте произведения А.С. Пушкина «Капитанская дочка» встречается имя Емельян в любом падеже.
Ответ: 2
11)При регистрации на сервере каждый пользователь получает уникальный персональный код, состоящий из двух частей. Первая часть кода содержит 12 символов, каждый из которых может быть одной из 26 заглавных латинских букв. Вторая часть кода содержит 5 символов, каждый из которых может быть одной из 9 цифр (цифра 0 не используется). При этом в базе данных сервера формируется запись, содержащая этот код и дополнительную информацию о пользователе. Для представления кода используют посимвольное кодирование, все символы в пределах одной части кода кодируют одинаковым минимально возможным для этой части количеством битов, а для кода в целом выделяется минимально возможное целое количество байтов. Для хранения данных о 30 пользователях потребовалось 2100 байт. Сколько байтов выделено для хранения дополнительной информации об одном пользователе? В ответе запишите только целое число – количество байтов.
Ответ: 60
13)На рисунке представлена схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И, К, Л, М, Н, П, Р, С. По каждой дороге можно передвигаться только в направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт С, проходящих через пункт К?
Ответ: 48
14)Значение выражения 3435 – 79 + 48 записали в системе счисления с основанием 7. Сколько цифр 6 содержится в этой записи?
15)Обозначим через ДЕЛ (n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа A формула (ДЕЛ(90, A) /\ (¬ДЕЛ(x, A) → (ДЕЛ(x, 15) → ¬ДЕЛ(x, 20))) тождественно истинна, то есть принимает значение 1 при любом натуральном x?
16)Обозначим через a mod b остаток от деления натурального числа a на натуральное число b. Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями: F(0) = 0; F(n) = n + F(n – 3), если n > 0 и при этом n mod 3 = 0; F(n) = n + F(n – (n mod 3)), если n mod 3 > 0. Чему равно значение функции F(22)?
17)Назовём натуральное число подходящим, если ровно два из его делителей входят в список (11, 13, 17, 19). Определите количество подходящих чисел, принадлежащих отрезку [11 000; 22 000], а также наименьшее из таких чисел. В ответе запишите два целых числа: сначала количество, затем наименьшее число.
18)Дана последовательность вещественных чисел. Из неё необходимо выбрать несколько подряд идущих чисел так, чтобы каждое следующее число отличалось от предыдущего не более чем на 10. Какую максимальную сумму могут иметь выбранные числа?
19)Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в четыре раза. Например, пусть в одной куче 7 камней, а в другой 9 камней; такую позицию мы будем обозначать (7, 9). За один ход из позиции (7, 9) можно получить любую из четырёх позиций: (8, 9), (28, 9), (7, 10), (7, 36). Чтобы делать ходы, у каждого игрока есть неограниченное количество камней.
20)Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания.
21)Для игры, описанной в задании 19, укажите такое значения S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
22)Ниже на четырёх языках программирования записана программа, которая вводит натуральное число x, выполняет преобразования, а затем выводит одно число. Укажите наименьшее возможное значение x, при вводе которого программа выведет число 120.
24)Текстовый файл содержит только заглавные буквы латинского алфавита (ABC…Z). Определите символ, который чаще всего встречается в файле сразу после буквы A. Например, в тексте ABCAABADDD после буквы A два раза стоит B, по одному разу – A и D. Для этого текста ответом будет B.
25)Рассмотрим произвольное натуральное число, представим его всеми возможными способами в виде произведения двух натуральных чисел и найдём для каждого такого произведения разность сомножителей. Например, для числа 16 получим: 16 = 16*1 = 8*2 = 4*4, множество разностей содержит числа 15, 6 и 0. Найдите все натуральные числа, принадлежащие отрезку [1 000 000; 2 000 000], у которых составленное описанным способом множество разностей будет содержать не меньше трёх элементов, не превышающих 100. В ответе перечислите найденные числа в порядке возрастания.
26)Для перевозки партии грузов различной массы выделен грузовик, но его грузоподъёмность ограничена, поэтому перевезти сразу все грузы не удастся. Грузы массой от 200 до 210 кг грузят в первую очередь. На оставшееся после этого место стараются взять как можно больше грузов. Если это можно сделать несколькими способами, выбирают тот способ, при котором самый большой из выбранных грузов имеет наибольшую массу. Если и при этом условии возможно несколько вариантов, выбирается тот, при котором наибольшую массу имеет второй по величине груз, и т.д. Известны количество грузов, масса каждого из них и грузоподъёмность грузовика. Необходимо определить количество и общую массу грузов, которые будут вывезены при погрузке по вышеописанным правилам.
27)Набор данных состоит из троек натуральных чисел. Необходимо распределить все числа на три группы, при этом в каждую группу должно попасть ровно одно число из каждой исходной тройки. Сумма всех чисел в первой группе должна быть чётной, во второй – нечётной. Определите максимально возможную сумму всех чисел в третьей группе.
Сложные задания с варианта ИН2010202:
Ответ: 21
6)Определите, при каком наименьшем введённом значении переменной s программа выведет число 57. Для Вашего удобства программа представлена на четырёх языках программирования.
Ответ: 16
7)Для хранения в информационной системе документы сканируются с разрешением 200 dpi и цветовой системой, содержащей 216 = 65 536 цветов. Методы сжатия изображений не используются. Средний размер отсканированного документа составляет 8 Мбайт. Для повышения качества представления информации было решено перейти на разрешение 300 dpi и цветовую систему, содержащую 224 = 16 777 216 цветов. Сколько Мбайт будет составлять средний размер документа, отсканированного с изменёнными параметрами?
Ответ: 27
8)Андрей составляет 6-буквенные коды из букв А, Н, Д, Р, Е, Й. Буква Й может использоваться в коде не более одного раза, при этом она не может стоять на первом месте, на последнем месте и рядом с буквой Е. Все остальные буквы могут встречаться произвольное количество раз или не встречаться совсем. Сколько различных кодов может составить Андрей?
Ответ: 23625
9)Электронная таблица содержит результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите, сколько раз за время наблюдений температура в 20:00 была ниже среднесуточной температуры того же дня.
Ответ: 28
20)Для игры, описанной в задании 19, найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания.
Ответ: 6*35
21)Для игры, описанной в задании 19, укажите такое значения S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Ответ: 34
22)Ниже на четырёх языках программирования записана программа, которая вводит натуральное число x, выполняет преобразования, а затем выводит одно число. Укажите наименьшее возможное значение x, при вводе которого программа выведет число 140.
Ответ: 329
24)Текстовый файл содержит только заглавные буквы латинского алфавита (ABC…Z). Определите символ, который чаще всего встречается в файле сразу после буквы E. Например, в тексте EBCEEBEDDD после буквы E два раза стоит B, по одному разу – E и D. Для этого текста ответом будет B.

Продолжаем разбор демонстрационного варианта ЕГЭ по информатике 2022.
В этой статье разберём с 6-ого по 10 задание.
Удачи на ЕГЭ по информатике 2022!
Определите, при каком наибольшем введённом значении переменной s программа выведет число 64. Для Вашего удобства программа представлена на четырёх языках программирования.
Решим задачу методом перебора на языке программирования Python.
Нас спрашивают, какое наибольшее число должен ввести пользователь программы, чтобы программа распечатала число 64. Мы будем подставлять каждое число в диапазоне, к примеру, от 1 до 1000 и попробуем получить на выходе число 64.
Делаем это с помощью цикла. Как только в переменной n будет значение 64, мы печатаем переменную i
Видим, что максимальное число, которое даёт нужный результат это 259.
Для хранения произвольного растрового изображения размером 128 × 320 пикселей отведено 20 Кбайт памяти без учёта размера заголовка файла. Для кодирования цвета каждого пикселя используется одинаковое количество бит, коды пикселей записываются в файл один за другим без промежутков. Какое максимальное количество цветов можно использовать в изображении?
Решение:
Узнаем, сколько информации будет весить один пиксель (одна точка).
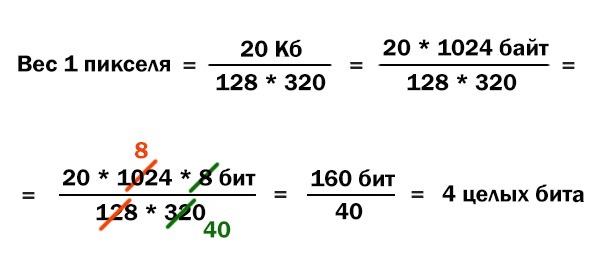
Теперь воспользуемся главной формулой для 7 задания из ЕГЭ по информатике.

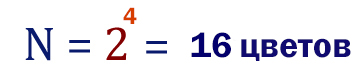
Ответ: 16
Все четырёхбуквенные слова, в составе которых могут быть только буквы Л, Е, М, У, Р, записаны в алфавитном порядке и пронумерованы, начиная с 1.
Ниже приведено начало списка.
Под каким номером в списке идёт первое слово, которое начинается с буквы Л?
Закодируем в правом столбце буквы цифрами, начиная с нуля.
Дальше кодирование прекращаем, т.к. буквы начинают повторяться.
Если представить список в виде цифр, то получится счёт в пятеричной системе, ведь у нас пять цифр.
1. 0000
2. 0001
3. 0002
4. 0003
5. 0004
6. 0010
В вопросе спрашивают про первое слово, которое начинается с буквы Л. А мы понимаем, что спрашивают про число 10005 в пятеричной системе, потому что это первое число, которое начинается с 1. Длина числа равна 4, т.к. длина слов равна 4.
Переведём число 10005 из пятеричной системы в нашу родную десятичную систему.
0*5 0 + 0*5 1 + 0*5 2 + 1*5 3 = 125
А порядковый номер (столбец слева) отличается от счёта в пятеричной системе на 1. Порядковый номер на 1 больше. Поэтому в ответе напишем 126.
Откройте файл электронной таблицы, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел может являться сторонами треугольника, то есть удовлетворяет неравенству треугольника.
В ответе запишите только число.
Неравенство треугольника заключается в том, что каждая сторона должна быть меньше, чем сумма двух других сторон.
Напротив тех строчек, которые удовлетворяют этому неравенству будем ставить 1, остальным ставим 0.
Сформируем формулу для первой строчки. Кликаем в ячейку D1 и нажимаем кнопку Вставить функцию.

Выбираем функцию ЕСЛИ. Пишем логическое выражение:
В Значение_если_истина ставим 1. В Значение_если_ложь ставим 0.
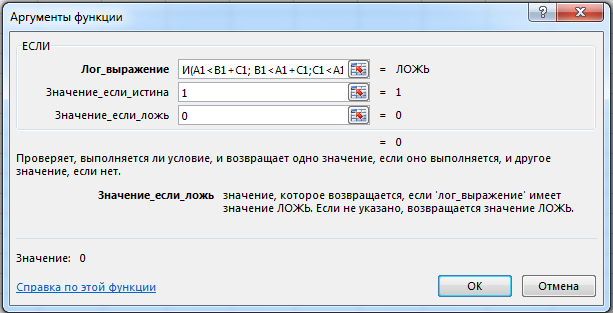
Если одновременно выполняются три условия, то в ячейку идёт 1, иначе 0.
Распространим формулу на весь столбец. Подведём курсор к правому нижнему углу. Как только загорелся чёрный крестик, кликаем два раза, и формула должна распространится на весь столбец.
Возле тех строчек, которые удовлетворяют условию, будут нули, возле тех, которые нет, будут единицы.
Найдём сумму столбца D. Это и будет количество троек, которые подходят в нашей задаче.
Кликаем по ячейке E1, нажимаем Вставить функцию и выбираем функцию СУММ. Там выбираем столбец D мышкой.
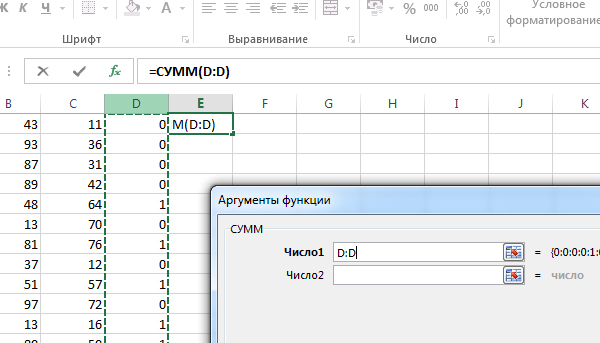
Нажимаем ОК, получается 2453.
Ответ: 2453
С помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «долг» или «Долг» в тексте романа в стихах А.С. Пушкина «Евгений Онегин». Другие формы слова «долг», такие как «долги», «долгами» и т.д., учитывать не следует. В ответе укажите только число.
Открываем соответствующий файл в программе Word. На вкладке "Главная" находится кнопка "Найти". Кликаем по чёрному треугольнику возле этой кнопки и выбираем "Расширенный поиск".
На вкладке "Главная" находится кнопка "Найти". Кликаем по чёрному треугольнику возле этой кнопки и выбираем "Расширенный поиск".

Далее, нажимаем кнопку "Больше>>".
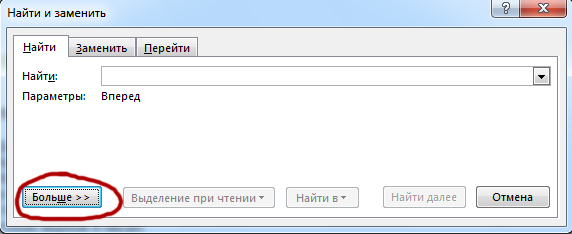
Теперь у нас есть все инструменты, чтобы решить 10 задание из ЕГЭ по информатике 2022.
В поле "Найти" пишем наше слово "долг". Галочку "Учитывать регистр" не ставим, т.к. слово может быть и с большой буквы. Но ставим галочку "Только слово целом".
Читайте также:


