Метод множителей лагранжа в excel
Метод лагранжевого множителя и реализация метода лагранжевого множителя на языке Python
Основная идея метода множителей Лагранжа
В качестве алгоритма оптимизации метод множителя Лагранжа в основном используется для решения задач оптимизации с ограничениями. Его основная идея состоит во введении n переменных путем введения множителей Лагранжа. Задача оптимизации с ограничениями с ограничениями k преобразуется в задача безусловной оптимизации с (n + k) переменными. Математический смысл множителя Лагранжа состоит в том, что он является коэффициентом каждого вектора в линейной комбинации градиента уравнения ограничения.
Как преобразовать задачу ограниченной оптимизации с n переменными и k ограничениями в задачу безусловной оптимизации с (n + k) переменными? Метод лагранжевых множителей начинается с математического смысла и устанавливает экстремальные условия путем введения лагранжевых множителей. Частные производные n переменных соответствуют n уравнениям, а затем k условий ограничения (соответствующих k лагранжевых множителей) вместе составляют систему уравнений (n + k) уравнения, содержащие (n + k) переменных, чтобы их можно было решить в соответствии с методом нахождения системы уравнений.

Википедия: Оптимальное решение
Зеленая линия отмечает траекторию точки, в которой ограничено g (x, y) = c. Синяя линия - это контур f (x, y). Стрелкой показан наклон, параллельный нормали к контуру.
С точки зрения градиента, очевидно, что d1> d2. Зеленая линия - это ограничение, то есть только точка, которая находится точно на этой зеленой линии, может соответствовать требованиям. Без этого ограничения минимальное значение f (x, y) должно приходиться на определенную точку внутри минимального контура. После добавления ограничения точка минимума, очевидно, должна находиться в положении, где линия контура f (x, y) точно касается линии ограничения, потому что, если она только пересекает, это означает, что должны быть другие линии контура, ожидающие в Эта линия. Внутренняя или внешняя часть верхней линии увеличивает или уменьшает значение пересечения между новой контурной линией и целевой функцией. Только когда контурная линия касается кривой целевой функции, оптимальное значение может быть полученный.
Если мы также найдем градиент ∇g (x, y) для ограничения, градиент будет показан зеленой стрелкой на рисунке. Легко видеть, что если вы хотите, чтобы контуры целевой функции f (x, y) касались ограничений, градиенты их точек касания должны быть на прямой линии (наклоны f и g параллельны) .
Это когда решение оптимизируется: ∇f (x, y) = λ (∇g (x, y) -C) (где ∇ - оператор градиента; а именно: f gradient of (x) = λ * градиент g (x), λ является константой и может быть любым ненулевым действительным числом, что указывает на то, что левая и правая стороны находятся в одном направлении.)
То есть: ▽ [f (x, y) + λ (g (x, y) −c)] = 0λ ≠ 0
Тогда функция Лагранжа: F (x, y) = f (x, y) + λ (g (x, y) −c), когда она достигает крайнего значения, и f (x , y) равны, потому что g (x, y) −c равно нулю, когда F (x, y) достигает своего крайнего значения.
Когда min (F (x, λ)) принимает минимальное значение, его производная равна 0, то есть ▽ f (x) + ▽ ∑ni = λihi (x) = 0, то есть Градиенты f (x) и h (x) коллинеарны.
Короче говоря, когда F (x, λ) получает оптимальное решение, то есть F (x, λ) принимает экстремальное значение (производная равна 0, ▽ [f (x, y) + λ (g (x, y) −c)] = 0), градиенты f (x) и g (x) коллинеарны. На данный момент это оптимизация f (x) при условном ограничение g (x) решение.
пример

Для эллипсоида формула выглядит следующим образом. Найдите максимальный объем вписанного кубоида этого эллипсоида.
Эта проблема на самом деле является условной задачей с экстремальным значением, то есть в условиях задачи решитьf(x,y,z)=8xyzМаксимальное значение.
Сначала удалите z в соответствии с условиями, а затем внесите проблему преобразования в безусловное экстремальное значение, с которым нужно иметь дело. Но иногда это сделать очень сложно или даже невозможно, в настоящее время необходим метод множителя Лагранжа. Превратите проблему в
Затем нам нужно получить частную производную ** F (x, y, z, λ) **
Объедините первые три уравнения, чтобы получить:bx=ay、az=cx, Приведем четвертое уравнение для решения
Наконец, вернитесь к исходной формуле, чтобы найти максимальное значение, как показано ниже.
Решение Python
Проблема такая же, как в только что решенном примере.

Результаты приведены ниже:
Пример. Построить многочлен Лагранжа 3-й степени, если заданы значения в 4-х узлах интерполяции:
| xi | -1 |
| yi | -1 |
Решение: Многочлен Лагранжа для четырех узлов интерполяции запишется так –
Для вычисления значения многочлена в точке х можно воспользоваться электронными таблицами Exel (рис. 18). В ячейки А3:А6 и В3:В6 записываются соответствующие значения yi и xi. В ячейки С3:С6 – формулы для вычисления pi(x). В столбце D3:D7 вычисляется значение
| A | B | C | D |
| Вычисление многочлена Лагранжа | |||
| yi | xi | X | |
| -1 | -1 | =$D$2-B3 | =A3*(C5*C4*C6)/((B3-B4)*(B3-B5)*(B3-B6) |
| Копировать С3 в С6 | =A4*(C3*C5*C6)/((B4-B3)*(B4-B5)*(B4-B6) | ||
| =A5*(C3*C4*C6)/((B5-B3)*(B5-B4)*(B5-B6) | |||
| =A6*(C3*C4*C5)/((B6-B3)*(B6-B4)*(B6-B5) | |||
| Значение L3(x) | =СУММ(D3:D6) |
4 .Варианты лабораторных работ для решения алгебраических и трансцендентных уравнений .
Задания: На отрезке [-10, 10] определить корни следующих уравнений:
8. x^3 – 0,1x^2+0,4x-1,5=0
5. Варианты лабораторных работ для решения систем линейных алгебраических уравнений .
Найти решение системы линейных уравнений методом итераций с точностью е=10-3:
Варианты лабораторных работ для решения систем линейных алгебраических уравнений .
Найти решение системы линейных уравнений методом итераций с точностью е=10-3:
Варианты лабораторных работ для решения систем линейных алгебраических уравнений .
Найти решение системы линейных уравнений методом итераций с точностью е=10-3:
Варианты лабораторных работ для решения систем линейных алгебраических уравнений .
Найти решение системы линейных уравнений методом итераций с точностью е=10-3:
6. Варианты лабораторных работ для решения задач интерполирования .
Задания. Построить интерполяционный полином Лагранжа L(x). Вычислить приближенное значение F(x) с помощью L(x) в точке х= , выполнить вычисления с помощью Exel.
| xk | 0.1 | 0.3 | 0.4 | 0.6 |
| yk | -0.1 | 0.5 | 0.8 | 1.7 |
| xk | -1 | -0.5 | 0.1 | 0.4 |
| yk | 1.0 | 2.2 | 1.7 | 0.8 |
| xk | 1.1 | 1.2 | 1.4 | 1.7 |
| yk | -2.0 | -1.8 | -1.3 | -1.0 |
| xk | -1.0 | -0.5 | 0.3 | |
| yk | 0.9 | 0.7 | 0.4 | 0.8 |
| xk | 3.2 | 3.4 | 3.7 | |
| yk | -14 | -10 | -8 | -12 |
| xk | 1.0 | 3.0 | 7.0 | 10.0 |
| yk | 0.3 | 0.7 | 0.9 | 1.0 |
| xk | -10.0 | -8.0 | -5.0 | -2.0 |
| yk | 6.0 | 3.0 | 0.0 | -4.0 |
| xk | 2.0 | 3.0 | 5.0 | 6.0 |
| yk | 0.7 | 1.2 | 2.2 | 3.0 |
| xk | 0.7 | 1.2 | 2.2 | 3.0 |
| yk | 0.8 | 1.0 | 1.3 | 1.2 |
| xk | ||||
| yk | 0.01 | 0.03 | 0.08 | 0.12 |
| xk | -10 | -8 | -5 | -2 |
| yk | -2 | |||
| xk | ||||
| yk | 0.1 | -0.2 | -0.3 | |
| xk | 2.0 | 3.2 | 4.2 | 5.6 |
| yk | -15 | -10 | -8 | -6 |
| xk | -4 | -3 | -2 | |
| yk | ||||
| xk | 10.5 | 11.5 | 12.5 | 13.0 |
| yk | -6 | -7 | -5 |
6. Варианты лабораторных работ для решения задач интерполирования .

Задания. Построить интерполяционный полином Лагранжа L(x). Вычислить приближенное значение F(x) с помощью L(x) в точке х= , выполнить вычисления с помощью Exel.
В случае, если для некоторой подзадачи ее нижняя оценка превосходит либо равна рекорду, такую подзадачу можно далее не ветвить, так как ее решение будет заведомо хуже либо не лучше решения, соответствующего рекорду.
В приведенном методе остается неопределенным способ выбора подзадачи для ветвления.
Такие способы могут быть различными. Наиболее употребимым является способ, при котором ветвят ту подзадачу, которой соответствует наименьшее значение нижней оценки либо ту, которая быстрее приведет к тривиальной подзадаче.
Различают методы ветвления в глубину и в ширину.
При ветвлении в глубину всегда ветвят одну из подзадач наибольшего уровня. Такое ветвление быстрее приведет к построению полного допустимого решения.
При ветвлении в ширину ветвят подзадачи одного уровня до тех пор, пока все такие подзадачи не будут рассмотрены. Такое ветвление позволяет получать больше нижних и верхних оценок и может привести к большему количеству отсеянных вариантов. Однако требуется больше памяти для хранения промежуточных результатов по сравнению с ветвлением в глубину.
Во многих экономических моделях исследования операций зависимости между постоянными и переменными факторами лишь в первом приближении можно считать линейными, более детальное рассмотрение позволяет обнаружить их нелинейность. Как правило, такие показатели, как прибыль, себестоимость, капитальные затраты на производство и др., в действительности зависят от объема производства, расхода ресурсов и т.п. нелинейно. В этом случае возникает задача нелинейного программирования, математическая модель которой формулируется следующим образом: найти переменные х1, х2, . хn, удовлетворяющие системе неравенств
и обращающие в максимум (или минимум) целевую функцию, т.е.
Можно выделить класс нелинейных задач, которые относятся к классическим методам оптимизации. Допустим, что среди ограничений нет неравенств, не обязательны условия неотрицательности, переменные не являются дискретными, т < п, а функции и непрерывны и имеют частные производные по крайней мере второго порядка. В этом случае задачу оптимизации можно сформулировать так: найти переменные х1, х2, . хn, удовлетворяющие системе уравнений
и обращающие в максимум (минимум) целевую функцию
Такие задачи в принципе можно решать классическими методами дифференциального исчисления. Однако на этом пути встречаются такие вычислительные трудности, которые делают необходимым поиск других методов решения. Поэтому классические методы часто используется не в качестве вычислительного средства, а как основа для теоретического анализа.
Другой способ определения условного экстремума начинается с построения вспомогательной функции Лагранжа, которая в области допустимых решений достигает максимума для тех же значений переменных х1, x2, . хn, что и целевая функция z.
Пусть решается задача определения условного экстремума функции z=f(X) при ограничениях, задаваемых так называемыми уравнениями связи
которая называется функцией Лагранжа, — постоянные множители (множители Лагранжа). Отметим, что множителям Лагранжа можно придать экономический смысл. Если — доход, соответствующий плану , а функция — издержки i-го ресурса, соответствующие этому плану, то — цена (оценка) i-го ресурса, характеризующая изменение экстремального значения целевой функции в зависимости от изменения размера i-го ресурса (маргинальная оценка). L(X) — функция п+т переменных . Определение стационарных точек этой функции приводит к решению системы уравнений
Легко заметить, что , то есть в систему входят уравнения связи. Таким образом, задача нахождения условного экстремума функции z = f(X) сводится к нахождению локального экстремума функции L(X). Если стационарная точка найдена, то вопрос о существовании экстремума в простейших случаях решается на основании достаточных условий экстремума — исследования знака второго дифференциала d 2 L(X) в стационарной точке при условии, что переменные приращения Dхj связаны соотношениями

полученными путем дифференцирования уравнений связи.
Пример. Найти наибольшее и наименьшее значения функции
при условии, что х1, х2, х3 удовлетворяют уравнению .
Решение.
Уравнение связи определяет в пространстве сферу единичного радиуса с
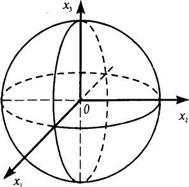 Рис. 4.2 | центром в начале координат (рис. 4.2). Так как сфера — замкнутое ограниченное множество, то согласно теореме Вейерштрасса функция достигает на ней своего наибольшего и наименьшего значений. Необходимо найти условный глобальный экстремум. Запишем уравнение связи в виде: . |
Составим функцию Лагранжа:
Найдем частные производные этой функции по .
Приравняв частные производные нулю, получим систему:
Решая систему, получим стационарные точки, в которых найдем значения функции z:
Выберем из всех значений z наибольшее и наименьшее: zmax = 1, а zmin=0.
интерполяционный многочлен Лагранжа.
Доброго времени суток.Помогите пожалуйста решить вот это)) Найти приближенное значение функции при.
Интерполяционный многочлен Лагранжа
Доброго времени суток. Не могу решить этот чертов хороший многочлен, весь день почти убил. Вот.

Интерполяционный многочлен Лагранжа
Доброго времени суток! Помогите пожалуйста составить программу, из-за курсовой совершенно ничего не.
Интерполяционный многочлен Лагранжа
1. Во всех вариантах требуется аппроксимировать заданную исходную функцию f(x) многочленом Лагранжа.
Но все равно спасибо. asd192, вам именно коэффициенты нужны или всё таки значение многочлена в какой-то точке?
asd192, Вам обязательно Лагранжем интерполировать, может достаточно будет аппроксимации, либо линейной интерполяции по двум точкам с помощью ПРЕДСКАЗ() или ТЕНДЕНЦИЯ(). Можете боллее детально описать задачу?
PS: Лагранжем я бы не советовал интерполировать, т.к может быть значительный разброс данных, к тому же для 102 точек придется рассчитывать полином 101 степени
вам именно коэффициенты нужны или всё таки значение многочлена в какой-то точке? В первом посте выложил >>>Аппроксимирующий полином.xls <<< . Там есть таблица значений. Вот по ней бы иличтобы потом по полиному Лагранжа высчитывать значения таблицы между точками которых в таблице нет.
В верхней строке и левом столбце - значения температуры, а в самой таблице - значения милливольт.
Т.е., например, вы меня научите как посчитать коэффициенты, а я потом подставлю их в полином Лагранжа и значение температуры и получу нужное мне значение милливольт.
Т.е. подставил температуру 30,7896 и получил соответствующее значение в милливольтах.
Читайте также:


