Как рассчитать дифференцированный платеж по кредиту в excel
В связи с короновирусом и ограничительными мерами есть возможность взять кредитные каникулы по ФЗ-106 от 03.04.2020. Выгодно ли это? У меня есть кредит и кредитка и я веду их графики платежей в MS Excel уже не первый год и мне это очень помогает в планировании.
Если спросите "Почему в Экселе, а не после каждого платежа запрашиваю график с пересчётом? Или можно просто смотреть на сумму следующего платежа и жать кнопку оплатить не заглядывая дальше?". Тогда я отвечу, что мне почему-то нравится планировать изменения в колонках сумм или сроков, когда я подставляю цифры: например, что будет если я погашу досрочно 10 тысяч в этом месяце или буду кидать на кредитку по 500 рублей в месяц больше.
С точки зрения MS Excel кредит это аннуитетные платежи, а кредитка - это дифференцированные.
Аннуитетные платежи в Excel
Мой кредит это 500 тысяч и страховка ещё 70 тысяч, банки очень любят не круглые проценты поэтому у меня 11,99% годовых. Всё это взято на 5 лет (платить естественно помесячно и накидываются проценты в конце периода - так у всех практически).
Можно зайти в википедию и посмотреть формулу расчёта аннуитета и набрать её в Экселе то получится такой расчёт:
коэффициент аннуитета =(K6*СТЕПЕНЬ(1+K6; K4))/(СТЕПЕНЬ(1+K6;K4)-1)
Но в Экселе есть стандартная функция =ПЛТ(11,99/12;60;570000) . Аргументы функции: Процент в период; Количество периодов; Сумма кредита. Для моего случая выйдет так и оно совпадает с точностью округления до копеек:
Если посмотреть в график из банка, то он будет отличаться на пару сотен. Как так? Идея в том, что периоды в году неравномерные (февраль короче, майские праздники прицепить могут к апрелю и тд), и на самом деле проценты рассчитываются для дней и потом объединяются в месяцы. Но сумма за год будет отличаться тоже максимум на пару сотен (проценты за новогодние праздники), поэтому это можно проигнорировать.
В случае досрочного погашения (тут столбец "ДП") можно выбрать варианты сократить срок кредита или уменьшить сумму платежа, в этом примере я вставил значением платёж, чтобы потом нагляднее было видно изменение параметров. Процент первой строки ввёл по концу периода (10 число месяца), но он написан в первом графике, так что его 1ый раз печатаем руками.
Можно посмотреть стоит ли напрягаться на досрочное погашение. В моём примере следует логичный вывод, что только в 1ый год досрочное погашение даёт выгоду по сравнению с 10% инфляции, которая была у нас в стране (про этот год и дальше не решаюсь даже предполагать).
Согласно ФЗ-106 от 03.04.2020 в случае отсрочки на полгода проценты начисляются, а срок не сдвигается.
Например взяли кредитные каникулы сейчас (ровно в середине периода), тогда сразу видно, что ежемесячный платёж сильно вырос и встаёт вопрос стоит ли полгода передышки этих 25 тысяч переплаты и возросшего на четверть ежемесячного платежа.
Дифференцированные платежи
Это когда проценты начисляются на задолженность в конце периода. У меня есть кредитка под 17,9% , по которой я накопил задолженность 100 тысяч рублей. Я планирую ещё сделать небольшой ремонт дома, а потом отдавать. Но по скольку я могу взять и потом отдавать? Делам простую табличку, в которую вносим ориентировочные траты и максимальные возможные погашения:
Автоматизировать процесс дифференцированного расчёта кредита можно при помощи кредитного калькулятора, разработанного в программе Microsoft Excel. В этой публикации мы вам расскажем и покажем, как это делается. Давайте приступим!
Где можно бесплатно скачать такой калькулятор
Не удивляйтесь, друзья, но вначале вам действительно надо скачать готовый калькулятор дифференцированных платежей, который мы разработали в Excel. Именно его мы и будем «разбирать на запчасти». Также, при желании, вы сможете его доработать под свои требования.
На примере этого калькулятора вы немного познакомитесь с программой Microsoft Excel, а также автоматизируете расчёт дифференцированных платежей по кредиту. Бесплатно скачать калькулятор можно перейдя по ссылке ниже:
Получилось? Вот и отлично! Приступаем к «разбору полётов»!
Разрабатываем калькулятор дифференцированных платежей в Excel
Прежде всего давайте разберемся, по какому принципу работает наш калькулятор. Откройте скачанный «экселевкий» файл. В верхнем левом углу страницы вы увидите две таблицы. Они называются: «Укажите данные для расчёта» и «Результаты расчёта». Также сверху над всеми столбцами нашей страницы Excel есть буквы A, B, C, D, E, F и т.д., а слева напротив строк – цифры 1, 2, 3, 4, 5, 6 и т. д. Именно эти буквы и цифры определяют координаты каждой ячейки таблицы.
Кликните левой кнопкой мыши по ячейке со значением «5958р.», которое находится в результатах расчёта в строке «Переплата по кредиту». В нашем калькуляторе эта ячейка имеет координаты B8. Вот вам картинка для наглядности:
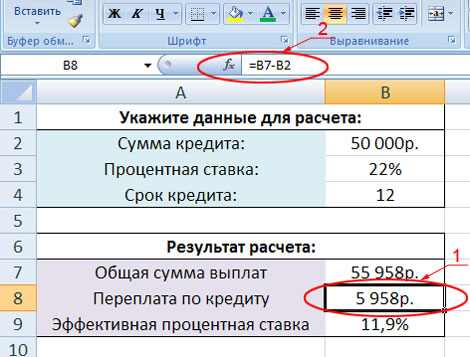
На изображении данную ячейку мы обвели красной линией и обозначили цифрой один. Обратите внимание ещё вот на что. Когда вы кликаете по какой-либо ячейке в таблице Excel, то эта ячейка выделяется чёрной жирной рамкой, а её буквенно-цифровые координаты сверху и слева окрашиваются другим фоном. Например, на нашем изображении буква B сверху и цифра 8 слева изменили цвет фона с серо-голубого на желтоватый. Также в верхней строке формул, слева от которой есть кнопка «fx» (на рисунке она обведена красным и обозначена цифрой два) указано значение или формула, по которой выполняется расчёт данных для выделенной ячейки. В нашем примере для ячейки с координатой B8 выполняется расчёт по следующей формуле: =B7-B2. В окне с координатой B7 указана общая сумма выплат по кредиту, которая в нашем примере равна 55 958 рублей, а B2 – это сам кредит, который равен 50 000 рублей. Выполнив простое математическое вычисление, наша программа занесла в ячейку B8 значение 5958 (55 958 – 50 000=5958).
Как видите, Microsoft Excel работает достаточно просто. По аналогичному принципу заданы формулы и значения для остальных ячеек нашего кредитного калькулятора дифференцированных платежей. Давайте рассмотрим, как они рассчитаны. Щёлкаем мышкой по изображению:
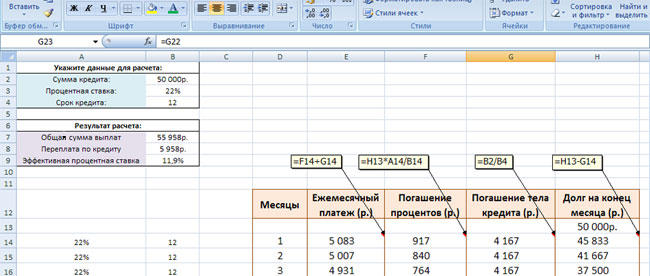
Итак, правее в оранжевой рамке вы видите график дифференцированных платежей по кредиту. Все значения в этой таблице рассчитываются автоматически по формулам, которые мы рассматривали в предыдущей публикации. Именно эти формулы и прописаны в ячейках нашего калькулятора. Давайте их детально рассмотрим на примере первой строки графика погашения кредита.
- «Ежемесячный платёж» – это ежемесячный дифференцированный платёж по займу. Он состоит из двух частей: суммы, идущей на погашение процентов (ячейка F14), и суммы, идущей на погашение тела кредита (ячейка G14). Именно потому ежемесячный платёж в первой строке рассчитан по формуле: =F14+ G14.
- «Погашение процентов» – здесь работает формула расчёта процентов по кредиту за данный период: остаток задолженности (в первом платеже он равен сумме кредита 50 000 руб., вынесенную в ячейку H13) умножить на годовую процентную ставку (она равна 22% и вынесена в ячейку A14) и разделить на 12 (мы вынесли это значение в ячейку B14). Собственно, эти условия и прописаны в формуле для ячейки F14: =H13*A14/B14. Кстати, вместо B14 можно просто указать фиксированную цифру – 12.
- «Погашение тела кредита» – это фиксированное значение, которое не меняется на протяжении всего срока кредитования. Рассчитывается этот показатель очень просто: сумма кредита (ячейка B2) делится на общий срок кредитования (ячейка B4). В итоге для ячейки G14 получаем такую формулу: = B2/B4.
- «Долг на конец месяца» – из суммы долга на конец предыдущего месяца (в первом платеже он у нас равен сумме кредита – 50 000 рублей и вынесен в ячейку H13) вычитаем выплату по телу кредита в текущем периоде (4167 рублей – ячейка G14). В результате, долг на конец месяца по первому платежу у нас равен 45 833 рубля (50 000 – 4167 = 45 833), что и записано в формуле для ячейки H14: = H13- G14.
Вот таким нехитрым способом разработан кредитный калькулятор дифференцированных платежей в Excel. Он рассчитан на кредиты сроком до 12 месяцев. При желании, вы можете его усовершенствовать и расширить данный диапазон до 24, 36 и более месяцев. В общем, теперь всё в ваших руках, друзья. Как говорится, мы вам дали удочку, а вы сами решайте, что с ней дальше делать.
Excel – это универсальный аналитическо-вычислительный инструмент, который часто используют кредиторы (банки, инвесторы и т.п.) и заемщики (предприниматели, компании, частные лица и т.д.).
Быстро сориентироваться в мудреных формулах, рассчитать проценты, суммы выплат, переплату позволяют функции программы Microsoft Excel.
Как рассчитать платежи по кредиту в Excel
Ежемесячные выплаты зависят от схемы погашения кредита. Различают аннуитетные и дифференцированные платежи:
- Аннуитет предполагает, что клиент вносит каждый месяц одинаковую сумму.
- При дифференцированной схеме погашения долга перед финансовой организацией проценты начисляются на остаток кредитной суммы. Поэтому ежемесячные платежи будут уменьшаться.
Чаще применяется аннуитет: выгоднее для банка и удобнее для большинства клиентов.
Расчет аннуитетных платежей по кредиту в Excel
Ежемесячная сумма аннуитетного платежа рассчитывается по формуле:
- А – сумма платежа по кредиту;
- К – коэффициент аннуитетного платежа;
- S – величина займа.
Формула коэффициента аннуитета:
К = (i * (1 + i)^n) / ((1+i)^n-1)
- где i – процентная ставка за месяц, результат деления годовой ставки на 12;
- n – срок кредита в месяцах.
В программе Excel существует специальная функция, которая считает аннуитетные платежи. Это ПЛТ:
- Заполним входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа, проценты и срок.
- Составим график погашения кредита. Пока пустой.
- В первую ячейку столбца «Платежи по кредиту» вводиться формула расчета кредита аннуитетными платежами в Excel: =ПЛТ($B$3/12; $B$4; $B$2). Чтобы закрепить ячейки, используем абсолютные ссылки. Можно вводить в формулу непосредственно числа, а не ссылки на ячейки с данными. Тогда она примет следующий вид: =ПЛТ(18%/12; 36; 100000).
Ячейки окрасились в красный цвет, перед числами появился знак «минус», т.к. мы эти деньги будем отдавать банку, терять.
Расчет платежей в Excel по дифференцированной схеме погашения
Дифференцированный способ оплаты предполагает, что:
- сумма основного долга распределена по периодам выплат равными долями;
- проценты по кредиту начисляются на остаток.
Формула расчета дифференцированного платежа:
ДП = ОСЗ / (ПП + ОСЗ * ПС)
- ДП – ежемесячный платеж по кредиту;
- ОСЗ – остаток займа;
- ПП – число оставшихся до конца срока погашения периодов;
- ПС – процентная ставка за месяц (годовую ставку делим на 12).
Составим график погашения предыдущего кредита по дифференцированной схеме.

Составим график погашения займа:

Остаток задолженности по кредиту: в первый месяц равняется всей сумме: =$B$2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(D10>$B$4;0;E9-G9). Где D10 – номер текущего периода, В4 – срок кредита; Е9 – остаток по кредиту в предыдущем периоде; G9 – сумма основного долга в предыдущем периоде.
Выплата процентов: остаток по кредиту в текущем периоде умножить на месячную процентную ставку, которая разделена на 12 месяцев: =E9*($B$3/12).
Выплата основного долга: сумму всего кредита разделить на срок: =ЕСЛИ(D9 Итоговый платеж: сумма «процентов» и «основного долга» в текущем периоде: =F8+G8.
Внесем формулы в соответствующие столбцы. Скопируем их на всю таблицу.

Сравним переплату при аннуитетной и дифференцированной схеме погашения кредита:

Красная цифра – аннуитет (брали 100 000 руб.), черная – дифференцированный способ.
Формула расчета процентов по кредиту в Excel
Проведем расчет процентов по кредиту в Excel и вычислим эффективную процентную ставку, имея следующую информацию по предлагаемому банком кредиту:

Рассчитаем ежемесячную процентную ставку и платежи по кредиту:

Заполним таблицу вида:

Комиссия берется ежемесячно со всей суммы. Общий платеж по кредиту – это аннуитетный платеж плюс комиссия. Сумма основного долга и сумма процентов – составляющие части аннуитетного платежа.
Сумма основного долга = аннуитетный платеж – проценты.
Сумма процентов = остаток долга * месячную процентную ставку.
Остаток основного долга = остаток предыдущего периода – сумму основного долга в предыдущем периоде.
Опираясь на таблицу ежемесячных платежей, рассчитаем эффективную процентную ставку:
- взяли кредит 500 000 руб.;
- вернули в банк – 684 881,67 руб. (сумма всех платежей по кредиту);
- переплата составила 184 881, 67 руб.;
- процентная ставка – 184 881, 67 / 500 000 * 100, или 37%.
- Безобидная комиссия в 1 % обошлась кредитополучателю очень дорого.
Эффективная процентная ставка кредита без комиссии составит 13%. Подсчет ведется по той же схеме.
Расчет полной стоимости кредита в Excel
Согласно Закону о потребительском кредите для расчета полной стоимости кредита (ПСК) теперь применяется новая формула. ПСК определяется в процентах с точностью до третьего знака после запятой по следующей формуле:
- ПСК = i * ЧБП * 100;
- где i – процентная ставка базового периода;
- ЧБП – число базовых периодов в календарном году.
Возьмем для примера следующие данные по кредиту:

Для расчета полной стоимости кредита нужно составить график платежей (порядок см. выше).

Нужно определить базовый период (БП). В законе сказано, что это стандартный временной интервал, который встречается в графике погашения чаще всего. В примере БП = 28 дней.
Далее находим ЧБП: 365 / 28 = 13.
Теперь можно найти процентную ставку базового периода:

У нас имеются все необходимые данные – подставляем их в формулу ПСК: =B9*B8
Примечание. Чтобы получить проценты в Excel, не нужно умножать на 100. Достаточно выставить для ячейки с результатом процентный формат.
ПСК по новой формуле совпала с годовой процентной ставкой по кредиту.
Таким образом, для расчета аннуитетных платежей по кредиту используется простейшая функция ПЛТ. Как видите, дифференцированный способ погашения несколько сложнее.
Кто как, а я считаю кредиты злом. Особенно потребительские. Кредиты для бизнеса - другое дело, а для обычных людей мышеловка"деньги за 15 минут, нужен только паспорт" срабатывает безотказно, предлагая удовольствие здесь и сейчас, а расплату за него когда-нибудь потом. И главная проблема, по-моему, даже не в грабительских процентах или в том, что это "потом" все равно когда-нибудь наступит. Кредит убивает мотивацию к росту. Зачем напрягаться, учиться, развиваться, искать дополнительные источники дохода, если можно тупо зайти в ближайший банк и там тебе за полчаса оформят кредит на кабальных условиях, попутно грамотно разведя на страхование и прочие допы?
Так что очень надеюсь, что изложенный ниже материал вам не пригодится.
Но если уж случится так, что вам или вашим близким придется влезть в это дело, то неплохо бы перед походом в банк хотя бы ориентировочно прикинуть суммы выплат по кредиту, переплату, сроки и т.д. "Помассажировать числа" заранее, как я это называю :) Microsoft Excel может сильно помочь в этом вопросе.
Вариант 1. Простой кредитный калькулятор в Excel
Для быстрой прикидки кредитный калькулятор в Excel можно сделать за пару минут с помощью всего одной функции и пары простых формул. Для расчета ежемесячной выплаты по аннуитетному кредиту (т.е. кредиту, где выплаты производятся равными суммами - таких сейчас большинство) в Excel есть специальная функция ПЛТ (PMT) из категории Финансовые (Financial) . Выделяем ячейку, где хотим получить результат, жмем на кнопку fx в строке формул, находим функцию ПЛТ в списке и жмем ОК. В следующем окне нужно будет ввести аргументы для расчета:

- Ставка - процентная ставка по кредиту в пересчете на период выплаты, т.е. на месяцы. Если годовая ставка 12%, то на один месяц должно приходиться по 1% соответственно.
- Кпер - количество периодов, т.е. срок кредита в месяцах.
- Пс - начальный баланс, т.е. сумма кредита.
- Бс - конечный баланс, т.е. баланс с которым мы должны по идее прийти к концу срока. Очевидно =0, т.е. никто никому ничего не должен.
- Тип - способ учета ежемесячных выплат. Если равен 1, то выплаты учитываются на начало месяца, если равен 0, то на конец. У нас в России абсолютное большинство банков работает по второму варианту, поэтому вводим 0.
Также полезно будет прикинуть общий объем выплат и переплату, т.е. ту сумму, которую мы отдаем банку за временно использование его денег. Это можно сделать с помощью простых формул:

Вариант 2. Добавляем детализацию
Если хочется более детализированного расчета, то можно воспользоваться еще двумя полезными финансовыми функциями Excel - ОСПЛТ (PPMT) и ПРПЛТ (IPMT) . Первая из них вычисляет ту часть очередного платежа, которая приходится на выплату самого кредита (тела кредита), а вторая может посчитать ту часть, которая придется на проценты банку. Добавим к нашему предыдущему примеру небольшую шапку таблицы с подробным расчетом и номера периодов (месяцев):

Функция ОСПЛТ (PPMT) в ячейке B17 вводится по аналогии с ПЛТ в предыдущем примере:

Добавился только параметр Период с номером текущего месяца (выплаты) и закрепление знаком $ некоторых ссылок, т.к. впоследствии мы эту формулу будем копировать вниз. Функция ПРПЛТ (IPMT) для вычисления процентной части вводится аналогично. Осталось скопировать введенные формулы вниз до последнего периода кредита и добавить столбцы с простыми формулами для вычисления общей суммы ежемесячных выплат (она постоянна и равна вычисленной выше в ячейке C7) и, ради интереса, оставшейся сумме долга:

Эта формула проверяет с помощью функции ЕСЛИ (IF) достигли мы последнего периода или нет, и выводит пустую текстовую строку ("") в том случае, если достигли, либо номер следующего периода. При копировании такой формулы вниз на большое количество строк мы получим номера периодов как раз до нужного предела (срока кредита). В остальных ячейках этой строки можно использовать похожую конструкцию с проверкой на присутствие номера периода:
=ЕСЛИ(A18<>""; текущая формула; "")
Т.е. если номер периода не пустой, то мы вычисляем сумму выплат с помощью наших формул с ПРПЛТ и ОСПЛТ. Если же номера нет, то выводим пустую текстовую строку:

Вариант 3. Досрочное погашение с уменьшением срока или выплаты
Реализованный в предыдущем варианте калькулятор неплох, но не учитывает один важный момент: в реальной жизни вы, скорее всего, будете вносить дополнительные платежи для досрочного погашения при удобной возможности. Для реализации этого можно добавить в нашу модель столбец с дополнительными выплатами, которые будут уменьшать остаток. Однако, большинство банков в подобных случаях предлагают на выбор: сокращать либо сумму ежемесячной выплаты, либо срок. Каждый такой сценарий для наглядности лучше посчитать отдельно.
В случае уменьшения срока придется дополнительно с помощью функции ЕСЛИ (IF) проверять - не достигли мы нулевого баланса раньше срока:

А в случае уменьшения выплаты - заново пересчитывать ежемесячный взнос начиная со следующего после досрочной выплаты периода:

Вариант 4. Кредитный калькулятор с нерегулярными выплатами
Существуют варианты кредитов, где клиент может платить нерегулярно, в любые произвольные даты внося любые имеющиеся суммы. Процентная ставка по таким кредитам обычно выше, но свободы выходит больше. Можно даже взять в банке еще денег в дополнение к имеющемуся кредиту. Для расчета по такой модели придется рассчитывать проценты и остаток с точностью не до месяца, а до дня:
Читайте также:


