Гипотрохоида как построить в excel
Большинство из тех, кто хоть раз строил графики в Microsoft Excel или PowerPoint, замечали необычный и забавный тип диаграмм - пузырьковые (bubble chart). Многие видели их в чужих файлах или презентациях. Однако, в 99 случаев из 100, при попытке самостоятельно построить такую диаграмму впервые, пользователи сталкиваются с рядом неочевидных сложностей. Обычно Excel или отказывается ее создавать вообще, или создает, но совершенно непонятного вида, без подписей и наглядности.
Давайте разберемся в этой теме.
Что такое пузырьковая диаграмма

По горизонтальной оси Х откладывается средний годовой доход на душу населения в USD. По вертикальной оси Y откладывается средняя продолжительность жизни в годах. Размер же (диаметр или площадь) каждого пузырька пропорционален населению каждой страны. Таким образом, на одной плоской диаграмме удается отобразить трехмерную информацию.
Дополнительную информационную нагрузку несет еще и цвет, отображающий региональную принадлежность каждой страны к определенному континенту.
Как построить пузырьковую диаграмму в Excel
Самый важный момент при построении пузырьковой диаграммы - правильно подготовленная таблица с исходными данными. А именно - таблица должна состоять строго из трех столбцов в следующем порядке (слева-направо):
- Параметр для откладывания по оси Х
- Параметр для откладывания по оси Y
- Параметр, определяющий размер пузырька
Возьмем для примера вот такую таблицу с данными по игровым приставкам:

Чтобы построить по ней пузырьковую диаграмму, нужно выделить диапазон C3:E8 (строго - только оранжевые и серые ячейки без столбца с названиями) и затем:
- В Excel 2007/2010 - перейти на вкладку Вставка- группа Диаграммы-Другие-Пузырьковая (Insert - Chart - Bubble)
- В Excel 2003 и старше - выбрать в меню Вставка - Диаграмма - Пузырьковая (Insert - Chart - Bubble)

Получившаяся в итоге диаграмма будет отображать быстродействие приставок по оси X, число программ для них по оси Y и долю рынка, занимаемого каждой приставкой - как размер пузырька:

После создания пузырьковой диаграммы имеет смысл настроить подписи к осям - без названий осей трудно понять, что по какой из них откладывается. В Excel 2007/2010 это можно сделать на вкладке Макет (Layout) , а в старых версиях Excel - щелкнув по диаграмме правой кнопкой мыши и выбрав команду Параметры диаграммы (Chart options) - вкладка Заголовки (Titles) .
К сожалению, Excel не позволяет автоматически привязывать цвет пузырьков к исходным данным (как в примере выше со странами), но для наглядности можно быстро отформатировать все пузырьки в разные цвета. Для этого щелкните правой кнопкой мыши на любом пузырьке, выберите команду Формат ряда данных (Format series) из контекстного меню и включите опцию Разноцветные точки (Vary colors) .
Проблема с подписями
Общей трудностью, с которой сталкиваются абсолютно все пользователи при построении пузырьковых (и точечных, кстати, тоже) диаграмм, являются подписи к пузырькам. Стандартными средствами Excel можно вывести в качестве подписей только значения X, Y, размер пузырька или называние ряда (общее для всех). Если вспомнить что при построении пузырьковой диаграммы вы не выделяли столбец с подписями, а только три столбца с данными X, Y и размер пузырьков, то все оказывается в общем-то логично: то, что не выделено - в диаграмму само никак попасть не может.
Решить проблему подписей можно тремя путями:
Способ 1. Вручную
Вручную переименовывать (менять) подписи для каждого пузырька. Можно просто щелкнуть мышью по контейнеру с подписью и ввести с клавиатуры новое название вместо старого. Очевидно, что при большом количестве пузырьков этот способ начинает напоминать мазохизм.
Способ 2. Надстройка XYChartLabeler
Нетрудно предположить, что с подобной проблемой до нас с вами сталкивались и другие пользователи Excel. И один из них, а именно легендарный Rob Bovey (дай бог ему здоровья) написал и выложил в открытый доступ бесплатную надстройку XYChartLabeler, добавляющую в Excel эту недостающую функцию.
После установки у вас появится новая вкладка (в старых версиях Excel - панель инструментов) XY Chart Labels:

Выделив пузырьки и воспользовавшись кнопкой Add Labels можно быстро и удобно добавить подписи сразу ко всем пузырькам в диаграмме, просто задав диапазон ячеек с текстом для подписей:

Способ 3. Excel 2013
В новой версии Microsoft Excel 2013 появилась наконец-таки возможность добавлять подписи к элементам данных диаграммы из любых произвольно выделенных ячеек. Дождались :)
Построить спираль Архимеда по следующим данным:
- в столбце А – значения угла t в радианах от 0 до 10 с шагом 0,2
- в столбце В – значения r = 0,5* t
- в столбце С – значения х = r * cos ( t )
- в столбце D – значения y = r * sin ( t )
- выделить значения в столбцах С и D и построить диаграмму
(тип: точечная с гладкими кривыми )
Построить астроиду по следующим данным:
- в столбце А – значения угла t в радианах от 0 до 7 с шагом 0,2
- в столбце В – значения х = 2*( cos ( t )) 3
- в столбце С – значения y = 2*( sin ( t )) 3
- выделить значения в столбцах B и С и построить диаграмму
(тип: точечная с гладкими кривыми )

Построить улитку Паскаля по следующим данным:
- в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
- в столбце В – значения t = a * π/180 (угол в радианах)
- в столбце С – значения p = cos ( t )–0,5
- в столбце D – значения x = p * cos ( t )
- в столбце Е – значения у = p * sin ( t )
- выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
Построить лемнискату Бернулли по следующим данным:
- в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
- в столбце В – значения t = a * π/180 (угол в радианах)
- в столбце С – значения r = 2* sin (2* t ) 2
- в столбце D – значения x = r * cos ( t )
- в столбце E – значения y = r * sin ( t )
- выделить значения в столбцах D и E и построить диаграмму
(тип: точечная с гладкими кривыми )
Построить график в форме сердца по следующим данным:
- в столбце А – значения a от 0 до 360 с шагом 10 (угол в градусах)
- в столбце В – значения t = a * π/180 (угол в радианах)
- в столбце С – значения x = 16*( sin ( t )) 3
- в столбце D – значения у =13* cos ( t )–5* cos (2* t )–2* cos (3* t )– cos (4* t )
- выделить значения в столбцах C и D и построить диаграмму
(тип: точечная с гладкими кривыми )
По сути, гипотрохоида представляет из себя кривую (узор), который формируется при движении одной окружности по внутренней стороне другой окружности. К сожалению, всё, что связано с геометрией, не всегда просто объяснить словами, требуются графики, анимация и картинки, которыми я внесу ясности в эту статью. Но суть не в этом…
Создание узоров, формируемых различными гипотрохоидами, можно легко рассчитать с помощью формул:
- x = (R-r)*cos(t) + h*cos( ((R-r)/r)*t );
- y = (R-r)*sin(t) - h*sin( ((R-r)/r)*t );
В целом, у нас есть три переменные, которые можно менять:
- R – радиус большого круга (статичный)
- r – радиус маленького круга (движется по внутренней поверхности большой окружности)
- h – длина прямой, которая выходит из центра маленького круга.
Собственно, конец прямой (точка), и будет создавать различные узоры (гипотрохоиды). Переменная t задаёт угол поворота.
Если немного поиска в интернете, то можно ещё найти такие понятия, как трохоида, эпитрохоида или гипоциклоида. Имеется даже детская игрушка спирограф, которая позволяет создавать узоры.
Однако, столь нудное введение потребовалось лишь для внесения некоторой ясности, основная цель статьи будет ясна далее.
Гипотрохоида – создание узоров программным путём
Пример генерации различных узоров
Нет, я сейчас не буду затрагивать тему программирования в стиле учебника, а всего лишь покажу применение.
Многие аспекты геометрии и математики в целом, нашли полноценное применение только с появлением компьютеров и языков программирования. Вот и я однажды решил вспомнить свои навыки в JavaScript и применить их на практике. Однако, навык программирования лучше всего наращивать при создании полноценного приложения – только в этом случае проявляются все тонкости языка. Понятно, что язык языку рознь – одни позволяют создавать прикладные программы, другие – интерактивные интернет страницы и так далее.
JavaScript довольно прочно стоит на платформе популярности, и позволяет не только оживлять интернет страницы, но и создавать полноценные графические редакторы, которых теперь довольно много.
Я решил сделать что-то своё. Вначале я сделал небольшой редактор для создания узоров на основе приведенных выше формул. Благодаря возможности задавать случайный цвет, использовать циклы и условные операторы, я решил поэкспериментировать. Большинство гипотрохоид (создаваемых узоров), напоминали 3D шар, но при уменьшении оборотов внутреннего круга, получались фигуры на подобие цветков.
Хм…. А это идея. JavaScript тег canvas содержит обширный набор функций для заливки, отрисовки и поворота холста и заданных контуров. Немного поигравшись, я прописал нужные параметры для рисования различных цветов. Ещё немного времени, и я добавил некое подобие кистей, в итоге – онлайн редактор для создания узоров позволял рисовать сплошной или контурный цветок в заданной точке холста, или шлейф из нескольких цветков.
Левая панель позволяла регулировать размер, количество создаваемых узоров, задавать случайный цвет и ряд других параметров.
От создания узоров до создания цветочного фона

Когда в твоих руках умение владеть программным кодом, то можно не только применять его для создания цветочных узоров (гипотрохоид), но и генерировать различный фон. Тут пришлось немного посидеть, поскольку, чем больше программного кода становиться, тем больше приходится учитывать мелких деталей. Так, если размер создаваемого узора большой, но один, то несколько десятков циклов для создания цветных переходов не влияют на скорость рисования. Другое дело – если нужно нарисовать фон из 100-200 различных цветочков с цветными переходами. В этом случае, генерация фона порождает ощутимую задержку, и приходиться добавлять дополнительные условные операторы, для сокращения времени выполнения.
Поскольку мой графический редактор при создании узоров и фона генерирует аналог цветка, то я решил его назвать Flower - цветочный генератор фона. Да, я понимаю, что подобного добра полно, но буду рад, если данный комок программного кода найдёт свою аудиторию.
В статье затрагивается тема создания различных узоров (гипотрохоид), на основе которых можно сделать довольно полезный графический редактор или генератор фона.
Используя заданные параметры, можно создавать фиксированные рисунки и узоры, а в связке с языком программирования, получаются великолепные рисунки и фоны.
Спасибо за внимание. Автор блога Владимир Баталий
9 февраля, 2014 Andrey K (30 голос, значение: 3,83 из 5)Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку

В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2. В другую ячейку формулу можно ввести аналогично (изменив D4 на D5) или использовать маркер автозаполнения.
В итоге мы получим табличку:

Теперь можно приступать к созданию графика.
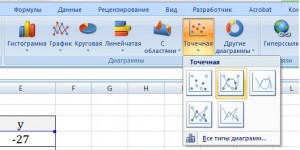
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
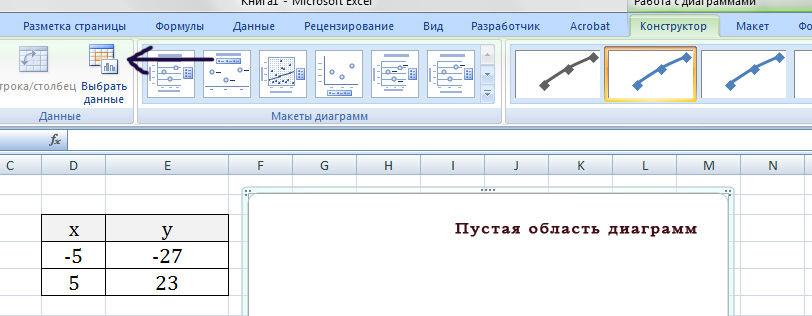

Нажимаем ОК. Перед нами график линейной функции.
Параболу по двум точкам уже не построить, в отличии от прямой.
Зададим интервал на оси x, на котором будет строиться наша парабола. Выберу [-5; 5].
Задам шаг. Чем меньше шаг, тем точнее будет построенный график. Выберу 0,2.
Заполняю столбец со значениями х, используя маркер автозаполнения до значения х=5.
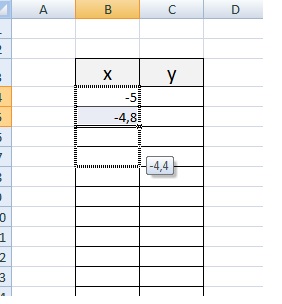
Столбец значений у рассчитывается по формуле: =2*B4^2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х.
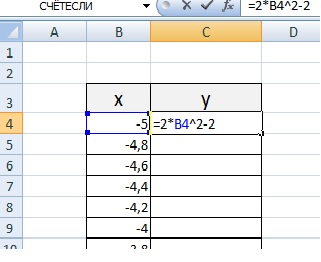

Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
Рассмотрим это на примере функции у=1/х.
Функция определена на интервалах (- беск;0) и (0; +беск)
Создадим график функции на интервалах: [-4;0) и (0; 4].
Подготовим две таблички, где х изменяется с шагом 0,2:

Находим значения функции от каждого аргумента х аналогично примерам выше.

Далее нажимаем кнопочку ДОБАВИТЬ и заполняем табличку ИЗМЕНЕНИЕ РЯДА значениями из второй таблички

Получаем график функции y=1/x

Читайте также:


