Что такое алгоритмы в 1с
Мне надо создать алгоритм документа (а именно Договоры), но как создавать алгоритм для 1С? (затруднение вызывает в частности Расшифровка, Меню.ДобавитьЗначение) - какими блоками все это делать?
Вобщем вопрос по документированию. Может есть какая ссылка куда-нибудь. Просто сложно представить, какими именно блоками рисовать все операции.
(2)ну так надо ответить, не ты ли искал сложные вопросыИнтересно, а Вау_куЛ'е ответ ещё нужен?
Лениво зря потеть так .
(9) Ладно. Уболтал , чёрт языкастый :-)
Бета-версия к завтрУ появится?
Ладно, раз непонятно, попытаюсь задать вопрос еще раз:
наверно, каждый из вас хоть раз в жизни (если вы программеры или что-то подобное) составляли блок-схему по программе. Так ведь? Вот, а мне нужен совет, как составить эту самую блок-схему по модулю 1С - там нет привычных мне блоков вычисления, присвоения - т.п.
Ничего если я вырезки из ЖКК приведу?
Никто ругаться не будет?
Встроенный язык (далее по тексту — язык) представляет собой предметно-ориентированный язык программирования, специально разработанный с учетом возможности его применения не только профессиональными программистами. В частности, все операторы языка имеют как русское, так и англоязычное написание, которые можно использовать одновременно в одном исходном тексте.
язык обладает некоторыми объектно-ориентированными возможностями, например, правила доступа к атрибутам и методам специализированных типов данных (документам, справочникам и т.п.) подобны свойствам и методам объектов, используемых в других объектно-ориентированных языках. Однако специализированные типы данных не могут определяться средствами самого языка, а задаются в визуальном режиме конфигуратора.
Типизация переменных в языке не жесткая, т.е. тип переменной определяется ее значением. Переменные не обязательно объявлять в явном виде. Неявным определением переменной является ее первое упоминание в левой части оператора присваивания. Возможно также явное объявление переменных при помощи соответствующего оператора. Допускается применение массивов.
Что такое программный модуль?
Программные модули в конфигурации системы 1C Предприятие не являются самостоятельными программами в общепринятом понимании этого слова, поскольку они являются только частью всей конфигурации задачи. Программный модуль — это своего рода "контейнер" для размещения текстов процедур и функций, вызываемых системой во время исполнения задачи в определенные моменты работы. Поэтому программный модуль не имеет формальных границ своего описания типа: "Начало модуля" — "Конец модуля".
Место размещения конкретного программного модуля (тот самый "контейнер") предоставляется конфигуратором в тех точках конфигурации задачи, которые требуют описания специфических алгоритмов функционирования. Эти алгоритмы следует оформлять в виде процедур или функций, которые будут вызваны самой системой в заранее предусмотренных ситуациях (например, при нажатии кнопки в диалоговом окне).
Каждый отдельный программный модуль воспринимается системой как единое целое, поэтому все процедуры и функции программного модуля выполняются в едином контексте.
Контекст выполнения программного модуля
Каждый программный модуль связан с остальной частью конфигурации задачи. Эта связь называется контекстом выполнения модуля. Следует различать два вида контекста:
• глобальный контекст задачи;
• локальный контекст выполнения конкретного модуля.
Глобальный контекст образуется:
модуля, объявленными с ключевым словом Экспорт.
Глобальный контекст виден всем программным модулям и определяет общую языковую среду конфигурации.
Локальный контекст модуля образуется тем конкретным местом конфигурации задачи, для которого использован программный модуль. Локальный контекст виден только конкретному программному модулю и определяет для модуля набор непосредственно доступных модулю значений агрегатных типов данных, их атрибутов и методов (см. «Виды программных модулей»). Однако, контекст модуля можно передать как объект в виде параметра при вызове процедур и функций (см. «Передача локального контекста программного модуля в качестве параметра»). Кроме того, контекст модуля определяет тот набор методов, которые доступны только в данном контексте (см. «Атрибуты и методы контекста Модуля формы», «Методы контекста Модуля формы элемента справочника» и т.п.). Локальный контекст предназначен для того, чтобы дать возможность управлять частными аспектами поведения задачи, присущими данному модулю.
В конкретном программном модуле любой из разделов может отсутствовать.
Раздел определения переменных размещается от начала текста модуля до первого оператора Процедура или опе-ратора Функция или любого исполняемого оператора. В этом разделе могут находиться только операторы объявления переменных Перем.
Раздел процедур и функций размещается от первого оператора Процедура или оператора Функция до любого ис-полняемого оператора вне тела описания процедур или функций.
Раздел основной программы размещается от первого исполняемого оператора вне тела процедур или функций до конца модуля. В этом разделе могут находиться только исполняемые операторы. Раздел основной программы исполняется в момент запуска модуля на выполнение (см. “Виды программных модулей”). Обычно в разделе основной программы имеет смысл размещать операторы инициализации переменных какими-либо конкретными значениями, которые необходимо провести до первого вызова любой из процедур или функций модуля.
(15) спасибо, конечно, но это совсем не то, что надо.
Я говорю не об определениях (что такое модуль, функции и т.д.), а о том, как рисовать блок-схему для модуля 1С.
Удивительное дело. Люди, стоявшие у истоков того, что мы сейчас называем computer science, считали "алгоритм" понятием в принципе неопределяемым. Таким же, как, например, "множество". Но, в отличие от "множества". Кстати, вы много видели определений множества? Кроме совсем смешного, типа: "множество - это совокупность чего-либо" (ага, ага, а совокупность - это множество чего-либо)? В отличие от "множества", в определениях "алгорима" недостатка нет. Вы без труда найдете штук пять или шесть.
Алгоритмом называется точное и понятное предписаниe исполнителю совершить последовательность действий, направленных на решение поставленной задачи.
Алгоритм — это последовательность действий для исполнителя, записанная на формальном языке и приводящая к заданной цели за конечное время.
Алгоритм - описание конечной последовательности шагов в решении задачи, приводящей от исходных данных к требуемому результату.
Алгоритм — конечная совокупность точно заданных правил решения произвольного класса задач или набор инструкций, описывающих порядок действий исполнителя для решения некоторой задачи.
Алгоритм — это всякая система вычислений, выполняемых по строго определённым правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи.
Алгоритм — это последовательность действий, либо приводящяя к решению задачи, либо поясняющая, почему это решение получить нельзя.
И хотя все эти определения - всего лишь чуть менее смешные, чем приведенное мной ранее определение "множества", такое упорство в общем неглупых людей наводит на мысль, что математики-основатели все-таки ошибались и определение алгоритма существует. Попробуем его найти, но сначала определимся с самим определением (извините за каламбур). Определение - это выражение некоторого сложного понятия через более простые. В идеале, оно должно состоять из одного существительного и одного прилагательного. Конечно, нечто может обладать множеством свойств, но обычно только одно из них являеся основным и определяющим. Его-то и следует выносить в определение, про все второстепенные можно спокойно забыть.
Я считаю что такое идеальное определение алгоритма есть. Математикам было сложно его найти, потому что оно, действительно лежит скорее в области физики, но оно есть. Прежде чем я вас с ним познакомлю, давайте разберемя - что не так со всеми прочими определениями.
Навскидку, можно увидеть, что почти в каждом есть слово "задача". Не знаю, как кто, но я бы не стал говорить , что "задача" это более простое понятие.
Дональд Кнут давал такое определение алгоритму:
Алгоритм — это конечный набор правил, который определяет последовательность операций для решения конкретного множества задач и обладает пятью важными чертами: конечность, определённость, ввод, вывод, эффективность.
Здесь мы опять видим "задачу", а также целых пять свойств. Наверняка здесь что-то лишнее.
Первое свойство - "конечность". Кнут определял его так:
Алгоритм всегда должен заканчиваться после конечного числа шагов.
Ха-ха-ха. "Всех впускать, никого не выпускать" через сколько ходов должно закончиться? А ведь это - алгоритм.
Видимо, количество тех, кому приходилось писать:
Второе свойство - определенность.
Каждый шаг алгоритма должен быть точно определен. Действия, которые нужно выполнить, должны быть строго и недвусмысленно определены для каждого возможного случая.
Для кого, простите, должны быть определены шаги алгоритма? Для исполнителя? Да, некоторые перефразируют этот момент у Кнута во что-то типа: "Алгоритм должен быть понятен исполнителю". Вообще, слово "должен" меня всегда настораживает. Я слишком хорошо знаю, что в этом мире никто никому ничего не должен. Но, допустим, что алгоритм именно должен, именно исполнителю и именно быть понятным. Вам понятно вот это?
А это - алгоритм из почтенного семейства алгоритмов Hello World! Он написан на некоторой разновидности брейнфака, которую я только что придумал. Понятен ли он исполнителю? А какому? Нет никакого исполнителя. Возможно он появится, если я напишу примерно шестьдесят строчек кода на C, Java или 1С. Но, скорее всего, я не стану этим заниматься. Видите в чем дело? Нам стоит признать, что алгоритм существует независимо от исполнителя. А как иначе? Алгоритм существует, пока его исполняют? А когда перестают исполнять, он исчезает?
Да, можно сказать, что этот алгоритм понятен мне, его создателю. Но это пока. Завтра я забуду, что я тут напридумывал, и что? Алгоритм исчезнет? А послезавтра я вспомню. Он возродится? Алгоритм существует независимо не только от исполнителя, но и от создателя. Иначе, как вы объясните тот факт, что Евклид, светлая ему память, уже давно прекратил делить большее на меньшее, а алгоритм Евклида все еще существует?
Алгоритм существует независимо от исполнителя и независимо от создателя. И, в принципе, может быть не понятен никому и, при этом, продолжать свое существование. Свойство определенности(понятности) можно убрать.
Третье свойство - ввод.
Алгоритм имее некоторое (возможно, равное нулю) число входных данных.
То есть, входные данные могут быть, а могут и отсутствовать (и это действительно так). Но если входные данные могут быть, а могут и не быть, то такое свойство для определения не важно.
Самое интересное четвертое свойство - вывод.
У алгоритма есть одно или несколько выходных данных.
То есть, мы должны прийти к какому то результату, решить какую-то задачу. Решить или решать постоянно (это в случае с бесконечными алгоритмами). Почему я говорю, что это свойство самое интересное? Потому что, слова "задача" или "результат" вы обнаружите в любом определении алгоритма.
Можно было бы сказать, что алгоритм - это способ решения задачи. Но это будет плохое определение. А что такое "задача"? Вот есть известный армейский алгоритм - "копать от забора и до обеда". На решение какой задачи будут направлены действия исполнителя? Могут ли существовать действия без задачи? А почему нет!
Нас невозможно сбить с пути, нам все равно, куда идти.
Можно ли описать такие действия? Ну, а какие проблемы!
"Задача", "результат", "цель" - все это лишнее, не приближает нас ни на шаг к пониманию сущности алгоритма.
Да, осталось еще пятое свойство. Но его никто, кроме автора, не воспринимал всерьез (возможно, что и автор тоже).
Эффективность. Алгоритм обычно считается эффективным, если все его операторы достаточно просты для того, чтобы их можно было точно выполнить в течение конечного промежутка времени с помощью карандаша и бумаги.
Итак у нас нет никаких пяти свойств. А также нет ни "задач", ни "результатов". Может показаться, что теперь у нас вообще ничего нет. Но это не так. Представьте себе лестницу из трех ступенек и робота с двумя ногами. Все что он может - это поставить правую или левую ногу на ступеньку под номером 1,2 или 3. Можно сказать что у нас есть всего шесть возможных команд: П1,П2,П3,Л1,Л2,Л3. Попробуйте написать алгоритм подъема снизу на самый верх этой коротенькой лестницы. У вас должно получиться что-то типа:
Есть ли какая-нибудь разница в том, с какой ноги начинать: с правой или с левой? Как вы понимаете, разницы никакой нет. Значит, можно начинать с любой ноги? С любой нельзя. Начинать надо конкретно с правой или конкретно с левой. Вы должны сделать выбор. И пока вы его не сделаете, робот будет стоять внизу.
В этом мире все имеет последствия, но не все имеет причину. Что-то когда-то начинается. У всякой цепочки причин-следствий есть первое звено. Способность создавать такое первое звено, давать начало называется волей.
У этого слова есть узкий, психобиологический смысл. И широкий, философский. Воля в широком смысле - это способность давать начало. Это - фундаментальное свойство нашего мира. В нашем примере с шагающим роботом мы сделали выбор из двух возможных вариантов. На такое элементарное, можно сказать однобитовое, проявление воли способно вообще все, начиная с фотона. Размер данной статьи не оставляет место для подробных разъяснений. Если кто заинтересуется данным вопросом, смотрите спор Бора с Энштейном, неравенства Белла и их экспериментальную проверку. Результаты последнего эксперимента, кстати, были опубликованы совсем недавно, в мае 2018 года.
Безусловно, алгоритм - это проявление воли. Но не только. Для того, чтобы создать алгоритм, мы должны сделать еще кое-что. Мы дожны дать нашей воле свободу. Освободить ее от себя. Обеспечить ее независимое существование от нас, ее родителя. В сущности, алгоритм и есть такая освобожденая от родителя воля. Освобождение от родителя (или опекуна) называетя словом "эмансипация". Поэтому окончательное определение алгоритма выглядит так:
Алгоритм - это эмансипированная воля.
Как я и обещал, здесь у нас одно существительное и одно прилагательное. Кроме того, "эмансипация" и "воля" - понятия более простые, чем определяемое. Поэтому, я нахожу это определение идеальным. Алгоритм - эмансипированная воля. Создание алгоритма - эмансипация. А человек, который занимается созданием алгоритма - эмансипатор. Мне, кстати, никогда не нравилось слово "программист". Оно мне всегда казалось каким-то ругательным. В самом деле. Если есть "ПРОграммист", значит должен быть и "ЭПИграммист". И я бы предпочел, чтобы меня называли вторым словом. Потому что я сначала думаю и только ПОТОМ ("ЭПИ") пишу ("грамма"). А "ПРОграммист" сначала ("ПРО") пишет ("грамма") и только потом думает. Чтобы никому не было обидно, следует всех, кто занимается созданием алгоритмов называть эмансипаторами. Тем более, что это слово в точности отражает то, чем они занимаются.
Наверное, каждый из нас сталкивался с ситуацией, когда нужно выполнить большой объем вычислений или передать/получить большой объем информации за ограниченный промежуток времени. А сколько из нас остановилось на последовательном алгоритме и закрыли глаза на продолжительность выполнения? Ну и что, что 20 часов ведется расчет/отправка/получение (подчеркнуть нужное) каких-то данных? Ну, я «выжал» из системы все, что можно, быстрее не получится… При этом серверное железо загружено на минимум.
На самом деле, почти всегда доступна альтернатива в виде распараллеливания выполняемой задачи. Конечно, параллельные алгоритмы несколько сложнее — балансировка нагрузки, синхронизации между потоками, а так же, в случае разделяемых ресурсов, борьба с ожиданием на блокировках и избегание deadlock’ов. Но, как правило, оно того стоит.
Об этом мы сегодня и поговорим… в контексте 1С Предприятия.
Практически во всех современных языках есть необходимый инструментарий для реализации параллелизма. Но не везде этот инструментарий удобен для использования. Кто-то скажет: «Ну и что тут сложного и не удобного? Платформенный механизм фоновых заданий в руки и вперед!». На практике оказалось не так все просто. А что если задача бизнес-критичная? Тогда нужно обеспечить, во-первых, гарантированное выполнение заданий и, во-вторых, мониторинг работы подсистемы выполнения заданий.
- администратор для проведения регламентных работ завершил все сессии;
- внешний ресурс, требуемый на момент выполнения задания, был недоступен в течении какого-то времени;
- у части заданий после очередного обновления могут появится ошибки в коде, фоновое будет остановлено по эксепшену и, кроме записи в журнал регистрации, никому ничего не сообщит.
Хочется иметь возможность гибкого управления запускаемыми заданиями с обратной связью, с учетом ошибок, с гарантированным запуском, и все это примерно с той же легкостью, какая существует в других языках и фреймворках для параллельных заданий.
Для облегчения собственной жизни была разработана универсальная библиотека, позволяющая легко создавать параллельные алгоритмы с гарантированным выполнением в среде 1С Предприятия на базе фоновых заданий.
Область применения
- Использование параллельных вычислений в автоматизации бизнес процессов;
- Параллельное выполнение запросов в долгих отчетах/обработках;
- Процессы загрузки/выгрузки данных;
- Организация нагрузочного тестирования.
Основной принцип работы

Добавляется задание очень просто — нужно указать точку входа (путь к экспортному методу с серверным контекстом в общем модуле или модуле менеджера) и кортеж с параметрами в виде структуры:
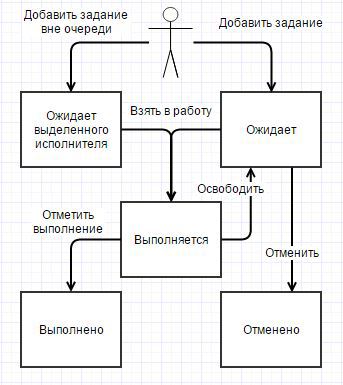
При этом происходит запись в регистр сведений мзЗадания. Первоначально задание имеет состояние Ожидает. Метод возвращает КлючЗадания для возможного отслеживания прогресса в основном клиентском потоке. Кортеж с параметрами так же расширяется свойством КлючЗадания, чтобы при выполнении задания был контекст, он иногда может быть полезен.
Далее, раз в минуту просыпается Менеджер, который первым делом проверяет исполнителей и освобождает задания, исполнители которых «умерли». Проверка заключается в следующем. Если задание в состоянии Выполняется и прописанное в качестве исполнителя фоновое не активно (удалено администратором, возникла исключительная ситуация в коде и т.д.), то задание возвращается в очередь. Для этого у задания выставляется состояние Ожидает.
Следующим шагом запрашиваются из очереди задания в соответствии с настройками балансировки нагрузки (сейчас это только ограничение на количество одновременно работающих исполнителей).
После этого Менеджер под каждое задание запускает Исполнителя. В качестве исполнителей выступают те самые фоновые задания платформы 1С.
При запуске Исполнитель делает отметку, что взял задание в работу — прописывает свой уникальный идентификатор у задания в свойстве КлючИсполнителя и выставляет состояние задания в Выполняется.
Когда задание выполнено, Исполнитель так же делает соответствующую отметку в задании — состояние Выполнено.
Для использования подсистемы в оперативном режиме есть метод ДобавитьЗаданиеВнеОчереди. При этом сразу запускается Исполнитель, минуя Менеджера, и забирает новое задание. Сигнатура такая же, как у основного метода ДобавитьЗадание. На такие задания ограничение на количество исполнителей НЕ распространяется, НО квота используется.
- У фоновых заданий вроде как есть метод отмены, но он работает для меня не прозрачно. Очень часто наблюдал картину, когда длительное фоновое задание дорабатывало до конца несмотря на отправленную команду отмены;
- Не хочется оставлять систему в неконсистентном состоянии. Кто знает, как именно написан код задания и что он делает в базе данных?
- ДождатьсяВыполнения(КлючиЗаданий, Таймаут = 5) — усыпляет текущий поток до выполнения указанного списка заданий, либо до истечения указанного времени;
- ОжидатьСостояниеЗадания(КлючЗадания, ОжидаемоеСостояние, Таймаут = 5) — усыпляет текущий поток до установления указанного состояния у задания, либо до истечения указанного времени;
- ОжидатьИзмененияСостояния(КлючЗадания, ТекущееСостояние, Таймаут = 5) — усыпляет текущий поток до изменения состояния у задания с указанного на любое другое, либо до истечения указанного времени.
Настройка
Для настройки есть специальная обработка «Управление менеджером заданий»:
- Ограничение на количество исполнителей — для балансировки нагрузки на сервере 1С. Принимает значение от 0 до 9999. При значении 0 задания в работу браться не будут.
- Глубина хранения истории (дни) — если указано значение отличное от 0, тогда подсистема сама будет чистить информацию по старым выполненным заданиям оставляя последние N дней указанных в настройке.
- Количество активных исполнителей;
- Количество заданий в очереди (в состоянии Ожидает);
- Всего активных заданий (п.1 + п.2).
Расширенный мониторинг сильно зависит от области применения и оставлен на откуп потребителям подсистемы.
Примеры использования
Использование параллельных вычислений в автоматизации бизнес процессов
Например, расчет заработной платы можно распараллелить по сотрудникам, потому что расчет зарплаты одного сотрудника, как правило, не зависит от расчета зарплаты другого сотрудника. (Приведенный код всего лишь иллюстрирует возможности подсистемы, и никак не связан с типовыми конфигурациями 1С.)
Параллельное выполнение запросов в долгих отчетах/обработках
Процессы загрузки/выгрузки данных
Организация нагрузочного тестирования
Исходники и прочее
Подсистема доступна на github/TaskManagerFor1C. CF файл открыт, так что можно ознакомиться с исходными кодами.
Подсистема разрабатывалась через тестирование (TDD), тесты доступны во внешней обработке /Тесты/Тесты_МенеджерЗаданий.epf. Для запуска тестов нужен инструментарий xUnitFor1C.
Обратная связь приветствуется. С удовольствием отвечу на все возникшие по инструменту вопросы.
Работа с числовыми матрицами в целом и решение систем линейных алгебраических уравнений в частности — классическая математическая и алгоритмическая задача, широко используемая при моделировании и расчёте огромного класса бизнес-процессов (например, при расчёте себестоимости). При создании и эксплуатации конфигураций «1С:Предприятия» многие разработчики сталкивались с необходимостью вручную реализовывать алгоритмы расчёта СЛАУ, а после — с проблемой длительного ожидания решения.
«1С:Предприятие» 8.3.14 будет содержать функциональность, позволяющую значительно сократить время решения систем линейных уравнений за счёт использования алгоритма, основанного на теории графов.
Он оптимизирован для использования на данных, имеющих разреженную структуру (то есть содержащие не более 10% ненулевых коэффициентов в уравнениях) и в среднем и в лучшем случаях демонстрирует асимптотику Θ(n⋅log(n)⋅log(n)), где n — количество переменных, а в худшем (при заполненности системы
100%) его асимптотика сопоставима с классическими алгоритмами ( Θ(n 3 )). При этом на системах, имеющих
10 5 неизвестных, алгоритм показывает ускорение в сотни раз по сравнению с реализованными в специализированных библиотеках линейной алгебры (например, superlu или lapack).

Важно: статья и описанный алгоритм требуют понимания линейной алгебры и теории графов на уровне первого курса университета.
Представление СЛАУ в виде графа
Рассмотрим простейшую разреженную систему линейных уравнений:

Внимание: система сгенерирована случайным образом и будет использоваться далее для демонстрации шагов работы алгоритма
При первом же взгляде на неё возникает ассоциация с другим математическим объектом — матрицей смежности графа. Так почему бы не преобразовать данные в списки смежности, сэкономив оперативную память в процессе выполнения и ускорив доступ к ненулевым коэффициентам?
Для этого нам достаточно транспонировать матрицу и установить инвариант “A[i][j]=z ⇔ i-я переменная входит в j-е уравнение с коэффициентом z”, а после для всякого ненулевого A[i][j] построить соответствующее ребро из вершины i в вершину j.
Полученный граф будет выглядеть так:

Даже визуально он оказывается менее громоздким, а асимптотические затраты оперативной памяти снижаются с O(n 2 ) до O(n+m), где m — число коэффициентов в системе.
Выделение компонент слабой связности
Вторая алгоритмическая идея, которая приходит в голову при рассмотрении получившейся сущности: использование принципа “разделяй и властвуй”. В терминах графа это приводит к разделению множества вершин на компоненты слабой связности.
Напомню, компонента слабой связности — такое подмножество вершин, максимальное по включению, что между любыми двумя существует путь из рёбер в неориентированном графе. Неориентированный граф из исходного мы можем получить, например, добавлением к каждому ребру обратного (с последующим удалением). Тогда в одну компоненту связности будут входить все вершины, до которых мы можем дойти при обходе графа в глубину.
После разделения на компоненты слабой связности граф примет такой вид:

В рамках анализа системы линейных уравнений это значит, что ни одна вершина из первой компоненты не входит в уравнения с номерами второй компоненты и наоборот, то есть решать эти подсистемы мы можем независимо (например, параллельно).
Редуцирование вершин графа
Следующий шаг алгоритма — как раз то, в чём заключается оптимизация под работу с разреженными матрицами. Даже в графе из примера присутствуют “висячие” вершины, означающие, что в некоторые из уравнений входит всего одна неизвестная и, как мы знаем, значение этой неизвестной легко найти.
Чтобы определить такие уравнения, предлагается хранить массив списков, содержащих номера переменных, входящих в уравнение, имеющее номер этого элемента массива. Тогда, при достижении списком единичного размера, мы можем редуцировать ту самую “единственную” вершину, а полученное значение сообщить остальным уравнениям, в которые эта вершина входит.
Таким образом, вершину 3 из примера мы сможем редуцировать сразу, полностью обработав компоненту:
Аналогично поступим с уравнением 0, так как в него входит всего одна переменная:
Другие уравнения тоже изменятся после нахождения этого результата:
Граф принимает следующий вид:

Заметим, что при редуцировании одной вершины могут возникнуть другие, тоже содержащие по одной неизвестной. Так что этот шаг алгоритма стоит повторять до тех пор, пока возможно редуцирование хотя бы одной из вершин.
Перестроение графа
Простейший пример такого графа: каждая вершина имеет степень вхождения, равную двум, ни одну из вершин нельзя редуцировать.

В рамках оптимизации под разреженные матрицы предполагается, что такие подграфы будут иметь малый размер, однако, работать с ними всё-таки придётся. Для расчёта значений неизвестных, входящих в подсистему уравнений, предлагается использовать классические методы решения СЛАУ (именно поэтому во введении указано, что при матрице, у которой все или почти все коэффициенты в уравнениях ненулевые, наш алгоритм будет иметь ту же асимптотическую сложность, что и стандартные).
Например, можно привести оставшееся после редуцирования множество вершин обратно в матричный вид и применить к нему метод Гаусса решения СЛАУ. Таким образом мы получим точное решение, а скорость работы алгоритма будет уменьшена за счёт обработки не всей системы, а лишь некоторой её части.
Тестирование алгоритма

Системы имели размер от 1000 до 200000 неизвестных
Для сравнения быстродействия мы использовали наиболее популярные библиотеки для решения задач линейной алгебры, такие как superlu и lapack. Конечно, данные библиотеки ориентированы на решение широкого класса задач и решение СЛАУ в них никак не оптимизировано, поэтому различие в быстродействии оказалось значительным.

Тестирование библиотеки ‘lapack’

Тестирование библиотеки ‘superlu’
Приведём итоговое сравнение нашего алгоритма с алгоритмами, реализованными в популярных библиотеках:

Заключение
Даже если вы не являетесь разработчиком конфигураций «1С:Предприятие», идеи и методы оптимизации, описанные в данной статье, могут быть использованы вами не только при реализации алгоритма решения СЛАУ, но и для целого класса задач линейной алгебры, связанных с матрицами.
Для разработчиков же 1С добавим, что новая функциональность решения СЛАУ поддерживает параллельное использование вычислительных ресурсов, и можно регулировать количество используемых потоков вычисления.
Читайте также:


