Момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия
Темы кодификатора ЕГЭ: момент силы, условия равновесия твёрдого тела.
Статика изучает равновесие тел под действием приложенных к ним сил. Равновесие - это состояние тела, при котором каждая его точка остаётся всё время неподвижной в некоторой инерциальной системе отсчёта.
Условием равновесия материальной точки является равенство нулю равнодействующей (т. е. векторной суммы) всех сил, приложенных к точке. В этом случае наша точка будет двигаться равномерно и прямолинейно в произвольной инерциальной системе отсчёта. Значит, система отсчёта, связанная с точкой, также будет инерциальной, и в ней точка будет покоиться.
В случае твёрдого тела ситуация сложнее. Прежде всего, важно учитывать точку приложения каждой силы.
-Сила тяжести приложена в центре тяжести тела. Для тела простой формы центр тяжести совпадает с центром симметрии.
-Силы упругости и трения приложены в точке или в плоскости контакта тела с соприкасающимся телом.
Прямая линия, проходящая через точку приложения вдоль вектора силы, называется линией действия силы. Оказывается, точку приложения силы можно переносить вдоль линии её действия - от этого механическое состояние тела не изменится (в частности, равновесие не нарушится).
Для равновесия твёрдого тела недостаточно потребовать равенства нулю векторной суммы всех приложенных к телу сил.
В качестве примера рассмотрим пару сил - так называются две равные по модулю противоположно направленные силы, линии действия которых не совпадают. Пусть пара сил и приложена к твёрдому стержню (рис. 1 ).
 |
| Рис. 1. Пара сил |
Векторная сумма этих сил равна нулю. Но стержень покоиться не будет: он начнёт вращаться. В данном случае не выполнено второе условие равновесия твёрдого тела. Чтобы его сформулировать, нужно ввести понятие момента силы.
Как должна быть направлена линия действия силы, чтобы тело стало вращаться вокруг неподвижной оси? Для начала заметим следующее.
- Если линия действия силы параллельна данной оси, то вращения не будет.
- Если линия действия силы пересекает данную ось, то вращения не будет.
В каждом из этих случаев действие силы вызывает лишь деформацию твёрдого тела.
Чтобы началось вращение, линия действия силы и ось вращения должны быть скрещивающимися прямыми.
Без ограничения общности можно считать эти прямые перпендикулярными друг другу. Мы всегда можем этого добиться, разложив силу на две составляющие - параллельную и перпендикулярную оси вращения - и отбросив параллельную составляющую как не вызывающую вращения. Поэтому везде далее мы считаем, что все силы, действующие на тело, перпендикулярны оси вращения.
Момент силы.
Плечо силы - это расстояние от оси вращения до линия действия силы (т. е. длина общего перпендикуляра к двум этим прямым).
В качестве примера на рис. 2 изображён диск, к которому приложена сила . Ось вращения перпендикулярна плоскости чертежа и проходит через точку . Плечом силы является величина , где - основание перпендикуляра, опущенного из точки на линию действия
силы.
 |
| Рис. 2. Плечо силы |
Момент силы относительно оси вращения - это произведение силы на плечо:
Чтобы учесть также направление вращения, вызываемого действием силы, моменту силы приписывают знак. Именно, момент силы считается положительным, если сила стремится поворачивать тело против часовой стрелки, и отрицательным, если по часовой стрелке.
Условия равновесия.
Если тело имеет неподвижную ось вращения и если алгебраическая сумма моментов всех сил относительно этой оси обращается в нуль, то тело будет находиться в равновесии. Это так называемое правило моментов . Оказывается, что в этом случае обращается в нуль алгебраическая сумма моментов всех сил относительно любой другой оси, параллельной оси вращения.
В общем случае, когда твёрдое тело может совершать как поступательное, так и вращательное движение, мы имеем два условия равновесия.
1. Равна нулю векторная сумма всех сил, приложенных к телу.
2. Равна нулю алгебраическая сумма моментов всех сил, приложенных к телу, относительно данной оси вращения или любой другой оси, параллельной данной.
Так, в примере на рис. 1 алгебраическая сумма моментов пары сил не обращается нуль (оба момента положительны). Поэтому стержень не находится в равновесии.
При решении задач удобно использовать сформулированные выше условия равновесия в следующем виде.
1'. Силы уравновешены вдоль любой оси.
2'. Суммарный момент сил, вращающих тело в одну сторону, равен суммарному моменту сил, вращающих тело в другую сторону.
Сейчас мы разберём одну достаточно содержательную задачу по статике и посмотрим, как работают наши условия равновесия.
Задача. Однородная лестница опирается на гладкую вертикальную стену, образуя с ней угол . При каком максимальном значении лестница будет покоиться? Коэффициент трения между лестницей и полом равен .
Решение. Пусть лестница опирается о пол и стену в точках и соответственно (рис. 3 ). Расставим силы, действующие на лестницу.
 |
| Рис. 3. К задаче |
Поскольку лестница однородная, сила тяжести приложена в середине лестницы. Сила упругости пола и сила трения приложены в точке . На рис. 3 точка приложения этих сил немного смещена от точки внутрь лестницы; тем самым мы однозначно указываем, что силы приложены именно к лестнице (а не к полу).
Точно так же сила упругости стены приложена в точке . Поскольку стена гладкая, сила трения между стеной и лестницей отсутствует.
Воспользуемся условием 1'. Вдоль горизонтальной оси силы уравновешены:
Вдоль вертикальной оси силы также уравновешены:
Теперь переходим к правилу моментов - условию 2'. Какую ось вращения выбрать? Удобнее всего взять ось, проходящую через точку (перпендикулярно плоскости рисунка). В таком случае моменты сразу двух сил и обратятся в нуль - ведь плечи этих сил относительно точки равны нулю (поскольку линии действия сил проходят через эту точку). Ненулевые моменты относительно точки имеют силы и , которые стремятся вращать лестницу в разные стороны; стало быть, моменты данных сил должны быть равны друг другу.
Плечо силы - это длина перпендикуляра , опущенного из точки на линию действия силы . Плечо силы - это длина перпендикуляра , опущенного из точки на линию действия силы . Согласно правилу моментов имеем:
Пусть длина лестницы равна . Тогда . Подставляем эти соотношения в равенство моментов:
С учётом равенства (1) имеем вместо (3) :
Вспомним теперь, что в условии спрашивается максимальное значение . При максимальном угле лестница пока ещё стоит, но уже находится на грани проскальзывания. Это означает, что сила трения достигла своего максимального значения, равного силе трения скольжения:

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
- Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.

Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Плечо силы
Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.
Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.
Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.

То есть перпендикуляр, проведенный от точки опоры до линии действия силы —это плечо силы.
Рычаг
В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.
Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.

Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.
Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.

Момент силы
При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.
Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.
Момент силы — это векторное произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.
Момент силы
M = Fl
M — момент силы [Н*м]
F — сила [Н]
l — плечо [м]
Вернемся к примеру с дверями. Вот мы приложили силу к краю двери — туда, где самый длинный рычаг. Получаем некоторое значение момента силы.
Теперь ту же силу приложим ближе к креплению двери, там, где плечо намного короче. По формуле получим момент меньшей величины.
На себе мы это ощущаем таким образом: нам легче толкать дверь там, где момент больше. То есть, чем больше момент, тем легче идет вращение.

То же самое можно сказать про гаечный ключ. Чтобы закрутить гайку, нужно взяться за ручку дальше гайки.

В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения плеча.
Расчет момента силы
Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.
Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.
Расстояние между точками A и B — 3 метра.

Момент силы относительно точки A:
Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.
Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!

Момент силы относительно точки B:
Если известно расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).

Момент силы относительно точки B:
Правило моментов
Вернемся к нашим баранам качелям. Мы умудряемся на них качаться, потому что существует вращательное действие — момент. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.
Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.
Это условие выполняется относительно любой точки.
Правило моментов
M1 + M2 +. + Mn = M’1 + M’2 +. + M’n
M1 + M2 +. + Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м]
Давайте рассмотрим этот закон на примере задач.
Задача 1
К левому концу невесомого стержня прикреплен груз массой 3 кг.

Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?
Решение:
Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен mgL5 он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом:Mg4L5 — он вращает по часовой.

Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг
Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг
Задача 2
Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?

Решение:
По правилу рычага: FB/FA=|OA|/|OB| где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:
Ответ: расстояние ОА равно 30 см
Задача 3
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?

Решение:
По правилу рычага m1g*l1=m2g*l2
Отсюда m2=l1/l2*m1=3/2*0,2 = 0,3 кг
Ответ: Масса груза равна 0,3 кг
Задача 4
На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода?

Решение:

Система на рисунке состоит из трех блоков: двух подвижных и одного неподвижного. Назначение неподвижного блока заключается только в том, что он меняет направление действия силы, однако никакого выигрыша в силе при этом не возникает. Каждый подвижный блок, напротив, дает выигрыш в силе.
Определим силу, с которой натянута первая нить. Груз растягивает ее с силой:
T = mg = 10*10 = 100 Н
Рассмотрим теперь первый подвижный блок. Так как вся система статична, полная сила, действующая на этот блок, должна быть равна нулю. Первая нить тянет его направо с суммарной силой 2T, значит, натяжение второй нити тоже должно быть равно 2T (вот он — выигрыш в силе). Аналогичное рассмотрение для второго подвижного блока показывает, что натяжение провода должно быть равно
Ответ: натяжение провода равно 400 Н
Задача 5 — a.k.a самая сложная задачка
Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.

Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?
Решение:
Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Приравнивая моменты, получаем выражение для модуля силы тяжести
Алгебраическим моментом силыотносительно центра (точки) О называется произведение модуля силы на ее плечо.
Плечо – кратчайшее расстояние от центра (точки) О до линии действия силы.
Момент силы считается положительным, если сила стремится повернуть тело вокруг центра (точки) О против хода часовой стрелки и отрицательным, если сила стремится повернуть тело вокруг центра (точки) О по ходу часовой стрелки.
Свойства момента силы относительно центра:
1) момент силы относительно центра (точки) О не изменится при переносе силы вдоль линии ее действия;
2) момент силы относительно центра (точки) О равен нулю, когда линия действия силы проходит через эту точку (т.е. )
Векторным моментом силыотносительно центра (точки) О называется вектор , равный векторному произведению радиуса вектора точки приложения силы на вектор силы :
Вектор момента силы относительно центра (точки) О направлен таким образом, чтобы с его конца можно было бы видеть «стремление» силы вращать тело против хода часовой стрелки.
Моментом силы относительно оси называют произведение проекции силы на плоскость, перпендикулярную оси, на плечо этой проекции относительно точки пересечения оси с плоскостью.
Момент силы относительно оси будет положительным, если с положительного конца оси поворот, которой «стремится» совершить проекция силы на плоскость, перпендикулярную оси, виден происходящим против хода часовой стрелки. Момент силы относительно оси будет отрицательным, если с положительного конца оси поворот, которой «стремится» совершить проекция силы на плоскость, перпендикулярную оси, виден происходящим по ходу часовой стрелки.
Механический смысл величины состоит в том, что она дает математическую характеристику того вращения тела вокруг оси , которое стремится произвести сила.
Свойства момента силы относительно оси:
1) момент силы относительно оси равен нулю, если линия действия силы параллельна оси;
2) момент силы относительно оси равен нулю, если линия действия силы пересекает ось.
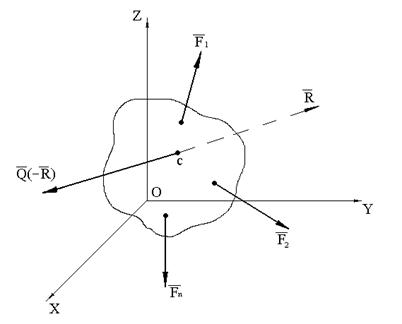
Теорема. Если данная система сил имеет равнодействующую, то момент равнодействующей относительно любой точки О равен сумме моментов сил относительно той же точки.
Пусть на тело действует система сил, имеющая равнодействующую , линия действия которой проходит через точку С, т.е. . Приложим дополнительно в точке С силу , которая равна по модулю, но противоположна по направлению равнодействующей силе , т.е.Q=-R.
Если Система сил расположена в одной плоскости, то теорема Вариньона выполняется и для алгебраических моментов сил, т.е.
Теоремой Вариньона часто бывает удобно пользоваться при вычислении моментов сил.

Определение
Моментом силы относительно точки (рисунок 1.1) называется векторное произведение радиус-вектора точки приложения силы на вектор силы.

Вектор момента направлен перпендикулярно плоскости, в которой лежат сила и точка, в ту сторону, откуда поворот от действия силы виден происходящим против хода часовой стрелки.
Наш короткий видеоурок про момент силы с примерами:
Вычисление момента
Вектор момента характеризует положение плоскости и направление вращательного действия силы, а также дает меру этого действия:
где h – плечо силы (кратчайшее расстояние от точки O – центра момента – до линии действия силы). Если сила проходит через точку, то ее момент относительно этой точки равен нулю.
Момент силы относительно точки не меняется от переноса силы вдоль линии ее действия.
Если силы расположены в одной плоскости, то используется понятие алгебраического момента силы.
Алгебраическим моментом силы относительно точки (или центра) называется взятое со знаком плюс или минус произведение модуля силы на плечо (рисунок 1.2).
Правило знаков

Если сила F задана своими проекциями на оси координат Fx, Fy, Fz и даны координаты x, y, z точки приложения этой силы, то момент силы относительно начала координат вычисляется следующим образом:

Проекции момента силы на оси координат равны:

Читайте также:


