Гриша сложил из бумаги 4 кораблика и 5 самолетов сколько всего поделок сделал гриша
А также два с половиной года на разработку схемы оригами.
Оригами-художник из Финляндии Юхо Конккёля создал из листа бумаги 95 на 96 сантиметров композицию в виде дуэли двух рыцарей. Он сделал это без разрезов и надрывов, согнув бумагу больше 5 тысяч раз. Об этом Конккёля рассказал в посте на Reddit.
Художник также рассказал, что разработал больше 25 вариантов схем, а на разработку композиции ему потребовалось два с половиной года. В итоге у него получилось произведение высотой в 25 сантиметров. Чтобы доказать, что рыцари сложены из одного листа, Конккёля опубликовал таймлайпс с процессом создания работы.
Это не первая работа, которую делает Конккёля. На его ютуб-канале есть ролики, где он рассказывает о процессе создания оригами в виде самурая, персонажа из игры NieR Replicant и средневековых рыцаря и копейщика.
Комбинаторные задачи — это задачи, решение которых требует рассмотрения и подсчёта все возможных случаев (всех возможных комбинаций).
2. Как называют схему, с помощью которой удобно и наглядно решать комбинаторные задачи?
Дерево возможных вариантов.
Решаем устно
1. Одним слоем бумаги оклеили куб, длина ребра которого равна 3 дм. Сколько квадратных дециметров бумаги потребовалось на оклеивание куба?
Найдём площадь поверхности куба:
S = 6a² = 6 • 3² = 6 • 9 = 54 (дм²) — бумаги потребовалось для оклеивания куба.
2. Объём прямоугольного параллелепипеда равен 240 см³. Какая из следующих троек чисел может задавать измерения этого параллелепипеда:
1) 4 см, 6 см, 12 см
4 • 6 • 12 = 24 • 12 = 288 (см³) — нет, эти числа не могут быть измерениями данного прямоугольного параллелепипеда.
2) 5 см, 6 см, 8 см
5 • 6 • 8 = 30 • 8 = 240 (см³) — да, эти числа могут быть измерениями данного прямоугольного параллелепипеда.
3) 3 см, 5 см, 10 см
3 • 5 • 10 = 15 • 10 = 150 (см³) — нет, эти числа не могут быть измерениями данного прямоугольного параллелепипеда.
4) 10 см, 10 см, 24 см
10 • 10 • 24 = 100 • 24 = 2 400 (см³) — нет, эти числа не могут быть измерениями данного прямоугольного параллелепипеда.
Ответ: числа 5 см, 6 см и 8 см.
3. Сколько центнеров пшеницы можно засыпать в бункер, имеющий форму прямоугольного параллелепипеда, если его длина равна 8 м, ширина — 2 м, высота — 1 м, а масса 1 м³ зерна составляет 8 ц?
1) 8 • 2 • 1 = 16 (м²) — объём бункера.
2) 16 • 8 = 128 (ц) — пшеницы можно засыпать в бункер.
Ответ: 128 центнеров.
4. Что больше и на сколько:
1) квадрат суммы чисел 4 и 3 или сумма их квадратов
(4 + 3)² > 4² + 3²
7² > 16 + 9
49 > 25
2) разность квадратов чисел 10 и 8 или квадрат их разности
10² — 8² > (10 — 8)²
100² — 64² > 2²
36 > 4
3) разность кубов чисел 5 и 3 или куб их разности
5³ — 3³ > (5 — 3)³
125 — 27 > 2³
98 > 8
Упражнения
645. Запишите все двузначные числа, в записи которых используются только цифры 1, 2 и 3 (цифры могут повторяться).
Таких двузначных чисел всего 9:
- 11, 12, 13
- 22, 21, 23
- 33, 31, 32
646. Запишите все двузначные числа, в записи которых используются только цифры 1, 2 и 0 (цифры могут повторяться).
Таких двузначных чисел всего 6:
647. У ослика Иа-Иа есть три надувных шарика: красный, зелёный и жёлтый. Он хочет подарить по одному шарику своим друзьям: Винни-Пуху, Пятачку и Кролику. Сколько у ослика Иа-Иа есть вариантов сделать подарки своим друзьям?

Итак, у нас получилось шесть возможных вариантов:
Винни-Пуха
Кролик
Вариант 1
Вариант 2
Вариант 3
Ответ: 6 вариантов.
648. Сколько двузначных чисел, все цифры которых различны, можно составить из цифр 0, 1 и 2?
Таких двузначных чисел всего 4:

Итак, у нас получилось шесть возможных вариантов (последовательно цвет шарика для Винни-Пуха, Пятачка и Кролика):
Вариант 1
Вариант 2
Вариант 3
Задача аналогична задаче № 647.
Ответ: 6 вариантов.
650. Запишите все трёхзначные числа, для записи которых используются только цифры (Цифры не могут повторяться.):
1) 3, 4 и 6
2) 4, 7 и 0
651. Сколько различных трёхзначных чисел можно составить из цифр (Цифры могут повторяться.):
1) 1 и 2
2) 0 и 1
652. Запишите все двузначные числа, в записи которых используются только цифры 2, 4, 9 и 0. (Цифры могут повторяться.)
- 22, 24, 29, 20
- 42, 44, 49, 40
- 92, 94, 99, 90
653. Сколько двузначных чисел можно составить из цифр 6, 7, 8 и 9 так, чтобы цифры были записаны в порядке возрастания?
654. Сколько двузначных чисел можно составить из цифр 6, 7, 8 и 9 так, чтобы цифры были записаны в порядке убывания?
655. Сколько существует двузначных чисел, сумма цифр которых равна 5?
Всего 5 чисел: 14, 23, 32, 41, 50.
656. Сколько двузначных чисел, сумма цифр которых равна чётному числу, можно составить из цифр 1, 2, 3, 4 (цифры могут повторяться)?
Всего 8 чисел: 11, 13, 22, 24, 31, 33, 42, 44.
657. Сколько двузначных чисел, сумма цифр которых равна нечётному числу, можно составить из цифр 0, 1,2, 3?
Всего 6 чисел: 10, 12, 21, 23, 30, 32.
658. Кот Базилио и лиса Алиса решили украсть золотой ключик, который хранится в каморке папы Карло. Чтобы туда проникнуть, нужно подобрать двузначный код. Им известно, что дверь в каморку закрывает Буратино, который знает пока что только четыре цифры: 0, 1, 2 и 3. Какое наибольшее количество вариантов придётся перебрать коту и лисе, чтобы открыть дверь?
- в первом столбце запишем возможные варианты первой цифры кода
- в верхней строке — возможные варианты второй цифры кода
- на пересечении строк и столбцов — возможные варианты кодов.
0
1
Итак, возможное количество вариантов кода — 16.
Ответ: 16 вариантов.
659. Сколько существует различных прямоугольников, периметры которых равны 24 см, а длины сторон выражены целым числом сантиметров?
Если P = 24 см, то сумма длин сторон равна 24 : 2 = 12 см.
Существует 6 возможных вариантов таких прямоугольников. Длины сторон у них должны быть:
- 1 см и 11 см
- 2 см и 10 см
- 3 см и 9 см
- 4 см и 8 см
- 5 см и 7 см
- 6 см и 6 см (квадрат, который также соответствует определению прямоугольника).
Ответ: 6 прямоугольников.
660. У Ани есть 30 одинаковых кубиков. Сколько различных прямоугольных параллелепипедов она может из них составить, если для построения одного параллелепипеда надо использовать все имеющиеся 30 кубиков?
Если V = 30, то можно подобрать 5 вариантов постройки прямоугольного параллелепипеда из одинаковых кубиков:
- 30 • 1 • 1 = 30
- 15 • 2 • 1 = 30
- 10 • 3 • 1 = 30
- 6 • 5 • 1 = 30
- 5 • 3 • 2 = 30
Ответ: 5 вариантов.
661. На прямой отметили четыре точки А, В, С и D. Сколько отрезков с концами в отмеченных точках можно провести? Какой из рисунков § 24 помогает решить эту задачу?
Для решения этой задачи можно ориентироваться на рисунок 184 § 24:
Но лучше сделать свой рисунок для этой конкретно задачи:

Ответ: 6 отрезков.
662. Подножие горы и её вершину связывают три тропы. Сколько существует маршрутов, ведущих от подножия к вершине и затем вниз к подножию?

Нарисуем эти три маршрута схематично, изобразив их в виде лучей, выходящих из единой точки, где:
- O — вершина горы
- A — первая точка у подножия горы
- B — вторая точка у подножия горы
- C — третья точка у подножия горы.
Тогда возможные следующие варианты маршрутов (начало маршрута — вершина — конец маршрута):
- AOA, AOB, AOC
- BOA, BOB, BOC
- COA, COB, COC
Итого — 9 вариантов маршрутов.
Ответ: 9 вариантов.
663. Спортивной команде предлагают футболки трёх цветов — красного, зелёного и синего, а шорты двух цветов — белого и жёлтого. Сколько вариантов выбора формы есть у команды?
- в первом столбце запишем возможные варианты шорт
- в верхней строке — возможные варианты футболок
- на пересечении строк и столбцов — возможные варианты формы
Форма
Синие
Шорты
Итак, возможное количество вариантов формы — 6.
Ответ: 6 вариантов.
664. У Тани есть четыре платья и две пары туфель. Сколько у Тани есть вариантов выбора наряда?
- в первом столбце запишем возможные варианты туфель
- в верхней строке — возможные варианты платьев
- на пересечении строк и столбцов — возможные варианты наряда
Наряд
4
Туфли
Итак, возможное количество вариантов нарядов — 8.
Ответ: 8 вариантов.
665. В отряде космонавтов есть три пилота и два инженера. Сколько существует способов составить экипаж, состоящий из одного пилота и одного инженера?
- в первом столбце запишем возможные варианты инженеров
- в верхней строке — возможные варианты пилотов
- на пересечении строк и столбцов — возможные варианты экипажа
Экипаж
3
Инженеры
Итак, возможное количество вариантов нарядов — 6.
Ответ: 6 вариантов.
666. На рисунке 185 изображён план одного района города. Отрезками изображены улицы. Сколько существует маршрутов из точки А в точку В, если передвигаться разрешено по улицам, идущими вверх или вправо?

Существуют следующие варианты маршрутов:
- Вверх — вверх — вправо — вправо
- Вверх — вправо — вверх — вправо
- Вверх — вправо — вправо — вверх
- Вправо — вверх — вверх — вправо
- Вправо — вверх — вправо — вверх
- Вправо — вправо — вверх — вверх
Итак, возможное количество вариантов маршрутов — 6.
Ответ: 6 вариантов.
Наибольшее значение выражения можно получить, если расставить знаки в таком порядке:
1 + 2 • 3 • 4 = 1 + 6 • 4 = 1 + 24 = 25.
Упражнения для повторения
668. Расстояние между двумя сёлами равно 28 км. Из этих сёл одновременно в одном направлении выехали мотоциклист и автобус. Автобус ехал впереди со скоростью 42 км/ч, а мотоциклист ехал со скоростью 56 км/ч. Через сколько часов после начала движения мотоциклист догонит автобус?

1) 56 — 42 = 14 (км/ч) — скорость, с которой мотоциклист догоняет автобус — скорость сближения.
2) 28 : 14 = 2 (часа) — время, за которое мотоциклист догонит автобус.
669. Решите уравнение:

670. 1) Одно из слагаемых в 14 раз больше другого. Во сколько раз их сумма больше меньшего слагаемого?
Пусть х — первое слагаемое. Тогда второе слагаемое равно 14х.
(14х + х) : х = 15х : х = 15
2) Вычитаемое в 12 раз больше разности. Во сколько раз уменьшаемое больше разности?
Пусть х — разность, тогда вычитаемое равно 12х, а уменьшаемое равно (12х + х).
(12х + х) : х = 13х : х = 13
671. На ферме есть 156 коров, каждая из которых даёт в день 12 л молока. Молоко с фермы вывозят в бидонах ёмкостью 40 л. В некоторый день на ферме было в наличии 42 пустых бидона. Хватит ли бидонов, чтобы вывезти с фермы надоенное за день молоко?
1) 156 • 12 = 1 872 (литра) — молока надаивают на ферме за 1 день.
2) 42 • 40 = 1 680 (литров) — молока помещается в 42 пустых бидона.
Ответ: Нет, не хватит.
672. Решите кроссворд.
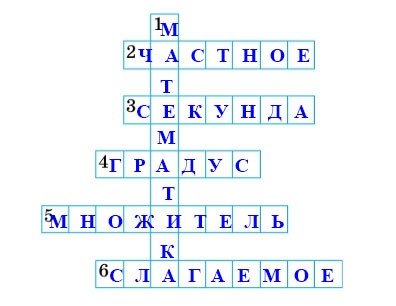
По горизонтали:
2. Результат арифметического действия (Частное)
3. Единица измерения времени (Секунда)
4. Единица измерения углов (Градус)
5. Компонент умножения (Множитель)
6. Компонент сложения (Слагаемое)
Задача от мудрой совы
673. В классе 30 учащихся. Они сидят по двое за 15 партами так, что половина всех девочек сидит с мальчиками. Можно ли учеников класса пересадить так, чтобы половина всех мальчиков сидела с девочками?
1) Если половина всех девочек сидят с мальчиками, значит вторая половина девочек сидит друг с другом по двое за партой. Значит половина девочек — это чётное количество человек.
2) Если половина девочек — это чётное количество человек, то общее количество девочек (две половины) также будет чётным числом.
3) Предположим, что условие задачи выполнимо и половину мальчиков можно посадить с девочками. Это значит, что другая половина мальчиков будет сидеть по двое за партой. То есть половина мальчиков также должно быть чётным числом.
4) Половина мальчиков и половина девочек — это ровно половина класса. По нашему предположению это чётное количество человек, так как и половина мальчиков, и половина девочек чётные числа.
5) Но мы знаем, что в классе 30 учащихся, а половина от 30 человек — это 15 человек — нечётное число. Значит наше предположение о мальчиках было неверно и их нельзя посадить так, чтобы половина мальчиков сидела с девочками.
— задачи трех категорий трудности: по 8 задач на 3 балла и на 4 балла, 4 задачи на 5 баллов (для 2 класса – 6, 6 и 3).
Все участники получают сертификат со своим результатом и памятный подарок.
Школы получают:
— дипломы и подарки лучшим участникам;
— сертификат победителям по параллели;
— отчет по параллелям;
— свидетельство школьному организатору;
— благодарственные письма для учителей, проводивших конкурс
Мероприятия проходят при поддержке таких авторитетных организаций, как:
— Санкт-Петербургское отделение математического института им. В. А. Стеклова РАН;
— Математический факультет Российского государственного педагогического университета им. А. И. Герцена;
1. Смартик сложил из спичек свое имя. В какой букве больше всего спичек?
2. Катя расположила числа 10, 7, 9, 3, 13, 5, 15 в порядке возрастания. Какое число она поставила предпоследним?
3. Что может получиться, если полоску, показанную на рисунке, склеить в кольцо, а потом разрезать в другом месте?
4. Робот может за один ход пройти или на три клетки вправо, или на две клетки вниз. Если следующий ход сделать нельзя, он останавливается. Робот начинает с клетки, отмеченной кружком. В какой клетке он остановится?
5. Винни-Пух собирался сделать одно важное дело. Если бы он начал в понедельник, то закончил бы в четверг. На самом деле он закончил в субботу. В какой день недели он начал?
Ответ: Б — в среду
6. На сколько разных цифр можно заменить звездочку, чтобы получилось двузначное число, большее 43?
7. В
8. Б
9. Б
10. Б
11. В
12. Г
13. В коробке лежат шарики. Среди фраз А-Д об этих шариках ровно одна неверная. Какая?
Ответ: Г — шариков 4 или меньше
14. Квадратный лист в клеточку 4х4 несколько раз согнули по линиям сетки. Сложенный лист проткнули один раз и разогнули обратно. Какая картинка могла получится?
15. В ребусе разные буквы заменяют разные цифры, а одинаковые буквы — одинаковые цифры. Смартик нашёл решение ребуса, в котором есть цифра 6. Какую цифру в этом решении заменяет буква И?
- Смартик выписал первые буквы названий всех цифр. Сколько из этих букв встречаются в слове СМАРТИК?
- Смартик построил домики из деталей трех видов. В каком из домиков меньше деталей, чем в остальных?
- Как называется одно из арифметических действий?
Ответ: Г — вычитание
4.Какое число получится, если выписать цифры, двигаясь по стрелочкам на рисунке?
- Электронные часы сейчас показывают 10 :10. Через сколько минут на часах будет тот же набор цифр?
- Прямоугольный коврик размером 2 × 3 сшит из шести квадратиков. Три таких коврика положили на пол, как показано на рисунке. В середину какого квадратика надо вбить гвоздик, чтобы приколотить к полу все три коврика?
- В альбоме с раскрасками Маша раскрашивает каждый день по одной картинке. Первую картинку она раскрасила в пятницу. В какой день Маша раскрасит пятую картинку?
Ответ: Г — во вторник
- У Насти на новогодней елке было 19 игрушек: шарики, звездочки и фонарики. Из них 10 игрушек — не шарики, а звездочек на 2 меньше, чем шариков. Сколько фонариков было на елке?
Задачи, оцениваемые в 4 балла
- Из лагеря выехала группа велосипедистов, всего 16 человек. Их маршрут обозначен стрелочками на рисунке. На каждой развилке велосипедисты делились на две равные группы. Сколько велосипедистов приехало в Комарово?
- Название какой цифры можно составить из букв слова СМАРТИК?
- Смартик склеил круг, квадрат и треугольник так, как показано на рисунке. Как выглядит его конструкция с другой стороны?
- Предпоследнее число четвертого десятка — это
- Смартик правильно заполнил схему на рисунке. В каких двух клетках оказались равные числа?
- Сначала Смартик выписал в ряд четные числа из набора 1, 2, 3, 4, 5, 6, 7, 8, 9 в порядке убывания, а потом справа приписал нечетные числа в порядке возрастания. Какой фрагмент есть в его ряду?
- В Цветочном городе коротышки учатся с понедельника по пятницу. Незнайка прогулял уроки в среду 1 сентября, после чего стал прогуливать каждый четвертый учебный день. Какой из следующих дней он прогулял?
Ответ: А — 9 сентября
- Три картонных прямоугольника 3 × 4 положили на клетчатый лист так, как показано на рисунке. Сколько клеток листа покрыто ровно двумя прямоугольниками?
- Электронные часы показывают 22 : 20. Через какое время они покажут тот же набор цифр?
Ответ: В — через 4 часа 2 минуты
Задачи, оцениваемые в 4 балла
- В турнире по теннису было 8 участников. Они разбились на пары и сыграли четыре матча, победители вновь разбились на пары и сыграли еще два матча. Наконец, победители этих матчей сыграли между собой финал. В этих семи матчах победили Вася, Аня, Миша, Аня, Толя, Аня, Миша (может быть, в другом порядке). Кто выиграл турнир?
Задачи, оцениваемые в 3 балла
- В клетки квадрата на рисунке Смартик вписал последовательно буквы своего имени. Он начал с центральной клетки и двигался по стрелкам. Какие две буквы оказались в соседних клетках?
- Смартик решал уравнение. Он понял: чтобы найти х, нужно сначала вычесть из числа 12 число 4, а потом результат поделить на 2. Что это было за уравнение?
- Смартик измерил два угла треугольника. Оказалось, что они равны 20° и 22°. Тогда этот треугольник
Ответ: Д — тупоугольный
- Смартик склеил круг, квадрат и треугольник так, как показано на рисунке. Как выглядит его конструкция с другой стороны?
- Винни-Пух два дня подряд ходит в гости к Кролику, потом два дня подряд ходит в гости к Пятачку, потом снова два дня к Кролику и так далее. В воскресенье он был в гостях у Пятачка. В какой из дней на следующей неделе он наверняка ходил к Кролику?
Ответ: Б — вторник
- На рисунке изображено несколько замкнутых линий. Смартик хочет соединить точку А с точкой В. Какое наименьшее число линий ему придется пересечь?
- Между какими двумя числами расположена дробь 2023/2022?
Ответ: В — 1,0001 и 1,001
- Из цифр года 2022 можно составить ровно одну дату: 22.02, то есть 22 февраля. Через сколько лет будет год, из цифр которого тоже можно составить ровно одну дату?
Задачи, оцениваемые в 4 балла
- У Маши есть 10 проволочных уголков (см. рисунок 1). Какое наименьшее число уголков нужно разогнуть, чтобы сложить контур, изображенный на рисунке 2?
На рисунке изображены три одинаковых квадрата. Чему равен отмеченный угол?
Чему равно наименьшее двузначное число, большее наибольшего двузначного числа, делящегося на 13?
Из города в Простоквашино в 14:00 выехал дядя Федор на велосипеде, и одновременно из Простоквашино выехал почтальон Печкин на тракторе. В 16:00 они встретились, а в 17:30 дядя Федор приехал в Простоквашино. Когда Печкин приехал в город?
На прямой отмечены точки А, В, С и D. Известно, что расстояние между А и В равно 2, между B и C — 3, а между С и D — 4 . Чему не может быть равно расстояние между А и D?
На какое наименьшее число нужно умножить 20²², чтобы получился куб натурального числа?
На сторонах равнобедренного треугольника ABC с основанием АС отмечены точки Е и D так, что BE=ED и AD=AC. Угол при вершине В равен 30°. Найдите угол EDA.

Человек с развитым логическим мышлением всегда заметно выделяется. Логическое мышление у детей необходимо развивать , начиная уже с дошкольного возраста. При обучении в школе развитая логика помогает ребенку успешнее учиться, справляться с математическими, и не только, задачами, ориентироваться в различных ситуациях.
В конце 4 класса все учащиеся пишут ВПР — Всероссийские проверочные работы. В настоящее время ВПР дети пишут по математике, русскому языку и окружающему миру.
Остановлюсь в этой статье на ВПР по математике. Из года в год задания носят достаточно стабильный характер. Встречаются очень простые задания на вычисление, несложные стандартные задачи. Это позволяет набрать необходимое количество баллов даже слабоуспевающему ученику.
Максимальный балл за выполнение работы — 20. Для положительного написания работы необходимо набрать хотя бы 6 баллов.
Отметка по пятибалльной шкале:
Простые задания оцениваются в 1 балл. За решение задач и нестандартных заданий ребенок получает 2 балла. Решение последней задачи, идущей под №12 позволяет ребёнку набрать максимальное количество баллов. Но задача это, как правило, логическая. Такие задачи чаще можно встретить при подготовке к олимпиадам, нежели просто в учебниках.
Логические задачи по математике
Задача №1
При записи номеров домов на улице Петровской было использовано 143 цифры. Сколько домов на этой улице? (Дома нумеруются с 1 и идут подряд, т.е. 1, 2, 3, 4 и т.д.)
Для записи номеров на первые девять домов требуется 9 цифр. Всего было использовано 143 цифры, а значит количество домов на улице выражено двузначным числом.
- 143 — 9 = 134 (цифры) — понадобилось на дома с двузначной нумерацией.
- 134 : 2 = 67 (домов) — с двузначной нумерацией.
- 9 + 67 =76 (домов) — всего на улице Петровской.
Подобные задачи для самостоятельного решения:
При записи номеров домов на улице Ивановской было использовано 157 цифр. Сколько домов на этой улице? (Дома нумеруются с 1 и идут подряд, т.е. 1, 2, 3,4 и т.д.)
При записи номеров страниц в детской книжке было использовано 177 цифр (страницы нумеруются с первой). Сколько страниц в книжке?
Задача №2
Полоску бумаги разрезали на три части. После этого самую большую из полученных частей снова разрезали на три части. Затем снова самую большую из полученных частей разрезали на три части. Так поступили много раз: на каждом шаге самую большую часть разрезали на три части. Могло ли в итоге получиться 100 частей?
Если кусок бумаги разрезать на три части, то общее количество частей увеличится на 2. Значит, общее количество частей после каждого шага будет нечётным. Но 100 — чётное число. Значит, 100 частей получиться в итоге не могло.
Ответ: нет, не могло.
Подобные задачи для самостоятельного решения:
Полоску бумаги разрезали на 5 частей. После этого самую большую из полученных частей снова разрезали на 5 частей. Затем снова самую большую из полученных частей разрезали на 5 частей. Так поступили много раз: на каждом шаге самую большую часть разрезали на пять 5. Могло ли в итоге получиться 399 частей?
Полоску бумаги разрезали на три части. После этого самую большую из полученных частей снова разрезали на три части. Затем снова самую большую из полученных частей разрезали на три части. Так поступили много раз: на каждом шаге самую большую часть разрезали на три части. Могло ли в итоге получиться 250 частей?
Полоску бумаги разрезали на 4 части. После этого самую большую из полученных частей снова разрезали на 4 части. Затем снова самую большую из полученных частей разрезали на 4 части. Так поступили много раз: на каждом шаге самую большую часть разрезали на 4 части. Могло ли в итоге получиться 293 части?
Полоску бумаги разрезали на 9 частей. После этого самую большую из полученных частей снова разрезали на 9 частей. Затем снова самую большую из полученных частей разрезали на 9 частей. Так поступили много раз: на каждом шаге самую большую часть разрезали на 9 частей. Могло ли в итоге получиться 997 частей?
Задача №3
Слава собирался купить 20 конфет, но ему не хватало для этого 3 руб. Тогда Слава купил 15 конфет, и у него осталось 7 руб. сдачи. Сколько стоит одна конфета?
Слава собирался купить 20 конфет, но купил 15 конфет. По условию у него осталось 7 руб.
Но он хотел купить на 5 конфет больше. Причём по условию ему не хватит 3 руб.
Подобные задачи для самостоятельного решения:
Максим хочет купить машинки (все они стоят одинаково). Если он купит пять машинок, то у него останется 50 руб., а до покупки семи машинок ему не хватает 10 руб. Сколько рублей стоит одна машинка?
Куртка на 700 руб. дешевле, чем пять шапок, но на 200 руб. дороже, чем две шапки. Сколько стоит шапка?
Задача №4
Вася с родителями собирал грибы. Мама нашла 9 грибов, папа нашёл 15 грибов, а Вася нашёл на столько же больше грибов, чем нашла мама, на сколько меньше, чем нашёл папа. Сколько грибов нашёл Вася?
Разность между числом папиных и маминых грибов равна 15-9=6 (грибов).
Значит 6:2=3 (гриба) — на столько Вася нашёл больше, чем мама и меньше, чем папа.
Вася нашёл 9+3=12 или 15-3=12 грибов.
Подобная задача для самостоятельного решения:
Коля с родителями собирал грибы. Мама нашла 18 грибов, папа нашёл 36 грибов, а Коля нашёл на столько же больше грибов, чем нашла мама, на сколько меньше, чем нашёл папа. Сколько грибов нашёл Коля?
Задача №4
Журавль стоит на двух ногах. А цапля — на одной ноге. Лягушка, сидя в болоте, насчитала 18 ног. Известно, что на болоте журавлей и цапель всего 11. Сколько на болоте цапель?
Если бы обе птицы стояли на двух ногах, то ног было бы 11·2=22 (ноги)
Но цапли стояли на одной ноге. Лягушка насчитала 18 ног.
Подобные задачи для самостоятельного решения:
6 трёхколёсных велосипедов.
Во дворе пасутся овцы и курицы. У овец и куриц вместе 36 голов и 100 ног. Сколько овец и сколько куриц?
14 овец и 22 курицы.
На лугу паслись лошади под присмотром пастухов. Если бы вы пожелали узнать, сколько всех ног на лугу, то насчитали бы 82 ноги. А если бы пересчитали головы, то оказалось бы, что всех голов — лошадиных и человеческих — 26. Сколько на лугу лошадей и сколько пастухов?
15 лошадей и 11 пастухов.
Задача №5
В школьной столовой два стакана компота, три пирожка с мясом и четыре пирожка с вишней стоят 105 руб., а три стакана компота, два пирожка с мясом и один пирожок с вишней – 75 руб. Сколько рублей заплатил мальчик за покупку в школьной столовой одного стакана компота, одного пирожка с мясом и одного пирожка с вишней?
Допустим, что мальчик сначала купил 2 стакана компота, 3 пирожка с мясом и 4 пирожка с вишней (заплатив за это 105 рублей).
Затем купил 3 стакана компота, 2 пирожка с мясом и 1 пирожок с вишней (заплатив 75 рублей).
Значит покупка, состоящая из 1 стакана компота, 1 пирожка с мясом и 1 пирожка с вишней, будет стоить: 180:5=36 рублей.
Ответ: 36 рублей.
Подобная задача для самостоятельного решения:
В школьном буфете две чашки чая, один пирожок и четыре конфеты стоят 48 руб., а четыре чашки чая, пять пирожков и две конфеты – 66 руб. Сколько рублей заплатил мальчик за покупку одной чашки чая, одного пирожка и одной конфеты?
Задача №6
Бабушке 51 год, а внуку один год. Через сколько лет бабушка будет в 3 раза старше внука?
Бабушка старше внука на: 51-1=50 лет.
Когда бабушка будет втрое старше внука, она всё равно будет старше его на 50 лет.
Но быть втрое старше внука – значит быть старше на два его возраста.
Значит, внуку будет при этом: 50: 2=25 лет. Так как сейчас ему один год, то это случится через 24 года.
Задача №7
Груш в саду в четыре раза меньше, чем вишен. Дети решили посчитать все деревья в саду. У Андрея получилось 55 деревьев, у Юры — 58, а у Игоря — 54. Известно, что один из них посчитал верно. Сколько деревьев в саду?
Поскольку груш в саду в 4 раза меньше, чем вишен, общее число деревьев должно делиться на 5.
Из полученных чисел только 55 делится на 5.
Подобная задача для самостоятельного решения:
Маша собирала грибы. Лисичек Маша собрала в три раза больше, чем сыроежек, а груздей столько же, сколько сыроежек. Маша решила посчитать все собранные грибы. Сначала у неё получилось 66 грибов, потом – 65, а в третий раз – 67. Известно, что один раз Маша посчитала верно. Сколько грибов собрала Маша?
Задача №8
Известно, что один холодильник, две микроволновые печи и три электрических чайника на 64 000 руб. дешевле, чем три холодильника, две микроволновые печи и один электрический чайник. На сколько холодильник дороже электрического чайника?
Если из обоих наборов удалить одинаковое количество одинаковых предметов, то разница в стоимости оставшихся наборов сохранится. Удалим из обоих наборов по две микроволновые печи, по одному холодильнику и по одному электрическому чайнику.
Тогда в первом наборе останется 2 электрических чайника, а во втором – 2 холодильника. Получаем, что 2 холодильника дороже двух электрочайников на 64 000 руб. Значит, 1 холодильник дороже 1 электрочайника на 32 000 руб.
Ответ: 32 000 руб.
Подобная задача для самостоятельного решения:
Известно, что четыре рубашки, три жилетки и одни брюки на 2000 руб. дешевле, чем две рубашки, три жилетки и трое брюк. На сколько брюки дороже рубашки?
Жилеток в обеих покупках одинаковое количество, значит они не влияют на разницу в стоимости покупки.
Тогда вся разница приходится на две рубашки и двое брюк. Получаем, что двое брюк дороже двух рубашек на 2000 рублей. Значит, одни брюки дороже одной рубашки на 1000 рублей.
Ответ: 1000 рублей.
Задача №9
Олег и Серёжа хотят купить книгу. У Олега есть только некоторое количество монет достоинством в 1 руб. Ему не хватает до покупки книги 135 руб. У Серёжи тоже есть деньги, но ему не хватает до покупки этой книги 2 руб. Если мальчики сложат свои деньги вместе, им всё равно не хватит денег на покупку книги. Сколько стоит книга?
Серёже не хватает до покупки 2 рублей. Поэтому у Олега меньше 2 руб., иначе при сложении денег вместе им хватило бы на покупку. Поскольку у Олега есть деньги, причём в однорублёвых монетах, то у него всего одна такая монета. Но Олегу не хватает до покупки 135 рублей Значит, книга стоит 1+135=136 рублей.
Ответ: 136 рублей.
Подобная задача для самостоятельного решения:
Света и Маша хотят купить куклу. У Светы есть только некоторое количество монет достоинством в 1 руб. Ей не хватает до покупки куклы 85 руб. У Маши тоже есть деньги, но ей не хватает до покупки этой куклы 2 руб. Если девочки сложат свои деньги вместе, им всё равно не хватит денег на покупку куклы. Сколько стоит кукла?
Задача №10
Андрей вырезал из бумаги несколько пятиугольников и шестиугольников. Всего у вырезанных фигурок 27 вершин. Сколько пятиугольников вырезал Андрей?
Предположим, что вырезал по две фигуры: 2 пятиугольника и 2 шестиугольника.
Вершин тогда получилось 5 · 2 + 6 · 2 = 22
Всего было 27 вершин, тогда 27 — 22 = 5, значит это тоже пятиугольник.
Ответ: 3 пятиугольника.
Подобные задачи для самостоятельного решения:
Паша вырезал из бумаги несколько пятиугольников и шестиугольников. Всего у вырезанных фигурок 32 вершины. Сколько шестиугольников вырезал Паша?
Оля вырезала из бумаги несколько пятиугольников и шестиугольников. Всего у вырезанных фигурок 34 вершины. Сколько шестиугольников вырезала Оля?
Задача №11
48 книг расставили по трём полкам, причём на первой полке оказалось на 3 книги меньше, чем на второй, а на третьей – на 6 больше, чем на второй. Сколько книг стоит на первой полке?
Уберём с третьей полки 6 книг, а на первую поставим 3 книги. Тогда общее количество книг на трёх полках уменьшится на 3.
Значит, всего книг станет 48 — 3 = 45.
При этом на всех трёх полках стало поровну книг, то есть по 45 : 3 = 15. Следовательно, исходно на первой полке стояло 15 — 3 = 12 книг.
Подобная задача для самостоятельного решения:
52 книги расставили по трём полкам, причём на первой полке оказалось на 3 книги меньше, чем на второй, а на третьей – на 4 больше, чем на второй. Сколько книг стоит на третьей полке?
Задача №12
В 10 часов утра на стадионе было 28 человек, из которых часть играли в футбол, а часть – в волейбол. Затем семь из игравших в футбол ушли со стадиона, а три человека, игравших в волейбол, пошли играть в футбол. В результате играющих в футбол стало в два раза больше, чем играющих в волейбол. Сколько человек играли в футбол в 10 часов утра?
После того как семь человек ушли со стадиона, на стадионе остался
Раз играющих в футбол стало в два раза больше, чем играющих в волейбол, то в футбол и волейбол играли в три раза больше человек, чем в волейбол.
Значит, в волейбол играли семь человек 21:3=7, а в футбол – 14 человек.
Следовательно, первоначально на стадионе играющих в футбол было 14+ 7- 3 =18 человек
Ответ: 18 человек.
В 9 часов утра на стадионе было 24 человека, из которых часть играли в футбол, а часть – в баскетбол. Затем шесть из игравших в футбол ушли со стадиона, а два человека, игравших в баскетбол, пошли играть в футбол. В результате играющих в футбол стало в два раза больше, чем играющих в баскетбол. Сколько человек играли в футбол в 9 часов утра?
Задача №13
В начале 2020 года в шкафу у Артура стояло 35 книг, некоторые из них он читал, а некоторые нет. До 23 февраля он прочитал пять книг, а на 23 февраля ему подарили четыре книги, которые он не читал. Вечером 23 февраля Артур заметил, что теперь прочитанных книг у него в два раза больше, чем тех, которые он не читал. Сколько прочитанных книг было у Артура в шкафу в начале 2020 года?
После 23 февраля у Артура стало 35 + 4 =39 книг.
Раз прочитанных книг у него стало в два раза больше, чем непрочитанных, то всего (прочитанных и непрочитанных) книг – в три раза больше, чем непрочитанных.
Значит, непрочитанных книг было 39 : 3= 13
Следовательно, первоначально у Артура была 26 — 5 = 21 прочитанная книга
Подобная задача для самостоятельного решения:
В начале 2020 года в шкафу у Ани стояло 33 книги, некоторые из них она читала, а некоторые нет. До 8 марта она прочитала четыре книги, а на 8 Марта ей подарили три книги, которые она не читала. Вечером 8 марта Аня заметила, что теперь прочитанных книг у неё в два раза больше, чем тех, которые она не читала. Сколько прочитанных книг было у Ани в шкафу в начале 2020 года?
Надеюсь статья была вам полезна. Если что-то непонятно или затрудняетесь с решением какой-либо задачи, то пишите в комментариях. Обязательно разберём.
Помогу с решением и подготовкой к ВПР вашему ребенку. Обращайтесь через форму обратной связи Контакты.
Рекомендую также статью: Логическое мышление. Как развить?
Читайте также:
- Поделка в сад к пасхе из ниток
- Конспект ручного труда в старшей группе поделка
- Доисторический остров поделки
- Как сделать юрту из бумаги
- Как сделать крафт бумагу в иллюстраторе


