Свободные электроны в металлах при отсутствии электрического поля
Электронная проводимость металлов была впервые экспериментально доказана немецким физиком Э.Рикке в 1901 г. Через три плотно прижатых друг к другу отполированных цилиндра — медный, алюминиевый и снова медный — длительное время (в течение года) пропускали электрический ток. Общий заряд, прошедший за это время, был равен 3.5·10 6 Кл. Поскольку массы атомов меди и алюминия существенно отличаются друг от друга, то массы цилиндров должны были бы заметно измениться, если бы носителями заряда были ионы. Результаты опытов показали, что масса каждого из цилиндров осталась неизменной. В соприкасающихся поверхностях были обнаружены лишь незначительные следы взаимного проникновения металлов, которые не превышали результатов обычной диффузии атомов в твердых телах. Следовательно, свободными носителями заряда в металлах являются не ионы, а такие частицы, которые одинаковы и в меди, и в алюминии. Такими частицами могли быть только электроны.
Прямое и убедительное доказательство справедливости этого предположения было получено в опытах, поставленных в 1913 г. Л. И. Мандельштамом и Н. Д. Папалекси и в 1916 г. Т. Стюартом и Р. Толменом.
На катушку наматывают проволоку, концы которой припаивают к двум металлическим дискам, изолированным друг от друга (рис. 1). К концам дисков с помощью скользящих контактов присоединяют гальванометр.
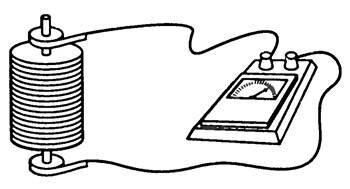
Катушку приводят в быстрое вращение, а затем резко останавливают. После резкой остановки катушки свободные заряженные частицы будут некоторое время двигаться вдоль проводника по инерции, и, следовательно, в катушке возникнет электрический ток. Ток будет существовать короткое время, так как из-за сопротивления проводника заряженные частицы тормозятся и упорядоченное движение частиц прекращается.
Направление тока говорит о том, что он создается движением отрицательно заряженных частиц. Переносимый при этом заряд пропорционален отношению заряда частиц, создающих ток, к их массе, т.е. \(~\Delta q = \frac\). Поэтому, измеряя заряд, проходящий через гальванометр за все время существования тока в цепи, удалось определить отношение \(~\frac\). Оно оказалось равным 1,8·10 11 Кл/кг. Эта величина совпадает с отношением заряда электрона к его массе, найденным ранее из других опытов.
Таким образом, электрический ток в металлах создается движением отрицательно заряженных частиц электронов. Согласно классической электронной теории проводимости металлов (П. Друде, 1900 г., Х.Лоренц, 1904 г.), металлический проводник можно рассматривать как физическую систему совокупности двух подсистем:
- свободных электронов с концентрацией ~ 10 28 м -3 и
- положительно заряженных ионов, колеблющихся около положения равновесия.
Появление свободных электронов в кристалле можно объяснить следующим образом.
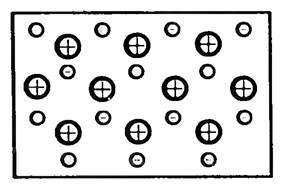
При объединении атомов в металлический кристалл слабее всего связанные с ядром атома внешние электроны отрываются от атомов (рис. 2). Поэтому в узлах кристаллической решетки металла располагаются положительные ионы, а в пространстве между ними движутся электроны, не связанные с ядрами своих атомов. Эти электроны называются свободными или электронами проводимости. Они совершают хаотическое движение, подобное движению молекул газа. Поэтому совокупность свободных электронов в металлах называют электронным газом.
Если к проводнику приложено внешнее электрическое поле, то на беспорядочное хаотическое движение свободных электронов накладывается направленное движение под действием сил электрического поля, что и порождает электрический ток. Скорость движения самих электронов в проводнике — несколько долей миллиметра в секунду, однако возникающее в проводнике электрическое поле распространяется по всей длине проводника со скоростью, близкой к скорости света в вакууме (3·10 8 м/с).
Так как электрический ток в металлах образуют свободные электроны, то проводимость металлических проводников называется электронной проводимостью.
Электроны под влиянием постоянной силы, действующей со стороны электрического поля, приобретают определенную скорость упорядоченного движения (ее называют дрейфовой). Эта скорость не увеличивается в дальнейшем со временем, так как при столкновении с ионами кристаллической решетки электроны передают кинетическую энергию, приобретенную в электрическом поле, кристаллической решетке. В первом приближении можно считать, что на длине свободного пробега λ (это расстояние, которое электрон проходит между двумя последовательными столкновениями с ионами) электрон движется с ускорением \(~a = \frac\) и его дрейфовая скорость линейно возрастает со временем\[~\upsilon = at = \frac\]. В момент столкновения электрон передает кинетическую энергию кристаллической решетке. Потом он опять ускоряется, и процесс повторяется. В результате средняя скорость упорядоченного движения электронов пропорциональна напряженности электрического поля в проводнике \(~\mathcal h \upsilon \mathcal i \sim E\) и, следовательно, разности потенциалов на концах проводника, так как \(~E = \frac Ul\), где l — длина проводника.
Известно, что сила тока в проводнике пропорциональна скорости упорядоченного движения частиц\[~I = en \mathcal h \upsilon \mathcal i S\], а значит, согласно предыдущему, сила тока пропорциональна разности потенциалов на концах проводника: I ~ U. В этом состоит качественное объяснение закона Ома на основе классической электронной теории проводимости металлов.
Однако в рамках этой теории возникли трудности. Из теории следовало, что удельное сопротивление должно быть пропорционально корню квадратному из температуры (\(~\rho \sim \sqrt T\)), между тем, согласно опыту, ρ ~ Т. Кроме того, теплоемкость металлов, согласно этой теории, должна быть значительно больше теплоемкости одноатомных кристаллов. В действительности теплоемкость металлов мало отличается от теплоемкости неметаллических кристаллов. Эти трудности были преодолены только в квантовой теории.
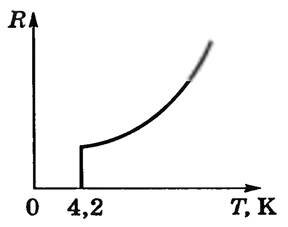
В 1911 г. голландский физик Г. Камерлинг-Оннес, изучая изменение электрического сопротивления ртути при низких температурах, обнаружил, что при температуре около 4 К (т.е. при -269 °С) удельное сопротивление скачком уменьшается (рис. 1) практически до нуля. Это явление обращения электрического сопротивления в нуль Г. Камерлинг-Оннес назвал сверхпроводимостью.
В дальнейшем было выяснено, что более 25 химических элементов — металлов при очень низких температурах становятся сверхпроводниками. У каждого из них своя критическая температура перехода в состояние с нулевым сопротивлением. Самое низкое значение ее у вольфрама — 0,012 К, самое высокое у ниобия — 9 К.
Сверхпроводимость наблюдается не только у чистых металлов, но и у многих химических соединений и сплавов. При этом сами элементы, входящие в состав сверхпроводящего соединения, могут и не являться сверхпроводниками. Например, NiBi, Au2Bi, PdTe, PtSb и другие.
Вещества в сверхпроводящем состоянии обладают необычными свойствами:
- электрический ток в сверхпроводнике может существовать длительное время без источника тока;
- внутри вещества в сверхпроводящем состоянии нельзя создать магнитное поле:
- магнитное поле разрушает состояние сверхпроводимости. Сверхпроводимость — явление, объясняемое с точки зрения квантовой теории. Достаточно сложное его описание выходит за рамки школьного курса физики.
Широкому применению сверхпроводимости до недавнего времени препятствовали трудности, связанные с необходимостью охлаждения до сверхнизких температур, для чего использовался жидкий гелий. Тем не менее, несмотря на сложность оборудования, дефицитность и дороговизну гелия, с 60-х годов XX века создаются сверхпроводящие магниты без тепловых потерь в их обмотках, что сделало практически возможным получение сильных магнитных полей в сравнительно больших объемах. Именно такие магниты требуются для создания установок управляемого термоядерного синтеза с магнитным удержанием плазмы, для мощных ускорителей заряженных частиц. Сверхпроводники используются в различных измерительных приборах, прежде всего в приборах для измерения очень слабых магнитных полей с высочайшей точностью.
В настоящее время в линиях электропередачи на преодоление сопротивления проводов уходит 10 - 15 % энергии. Сверхпроводящие линии или хотя бы вводы в крупные города принесут громадную экономию. Другая область применения сверхпроводимости — транспорт.
На основе сверхпроводящих пленок создан ряд быстродействующих логических и запоминающих элементов для счетно-решающих устройств. При космических исследованиях перспективно использование сверхпроводящих соленоидов для радиационной защиты космонавтов, стыковки кораблей, их торможения и ориентации, для плазменных ракетных двигателей.
В настоящее время созданы керамические материалы, обладающие сверхпроводимостью при более высокой температуре — свыше 100 К, то есть при температуре выше температуры кипения азота. Возможность охлаждать сверхпроводники жидким азотом, который имеет на порядок более высокую теплоту парообразования, существенно упрощает и удешевляет все криогенное оборудование, обещает огромный экономический эффект.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 279-282.
SA. Ток в металлах
В начале XX века была создана классическая электронная теория проводимости металлов (П. Друде, 1900 г., Х.Лоренц, 1904 г.), которая дала простое и наглядное объяснение большинства электрических и тепловых свойств металлов.
Рассмотрим некоторые положения этой теории.
Свободные электроны
Металлический проводник состоит из:
1) положительно заряженных ионов, колеблющихся около положения равновесия, и
2) свободных электронов, способных перемещаться по всему объему проводника.
Таким образом, электрические свойства металлов обусловлены наличием в них свободных электронов с концентрацией порядка 10 28 м –3 , что примерно соответствует концентрации атомов. Эти электроны называются электронами проводимости. Они образуются путем отрыва от атомов металлов их валентных электронов. Такие электроны не принадлежат какому-то определенному атому и способны перемещаться по всему объему тела.
В металле в отсутствие электрического поля электроны проводимости хаотически движутся и сталкиваются, чаще всего с ионами кристаллической решетки (рис. 1). Совокупность этих электронов можно приближенно рассматривать как некий электронный газ, подчиняющийся законам идеального газа. Средняя скорость теплового движения электронов при комнатной температуре составляет примерно 10 5 м/с.
Электрический ток в металлах
Ионы кристаллической решетки металла не принимают участие в создании тока. Их перемещение при прохождении тока означало бы перенос вещества вдоль проводника, что не наблюдается. Например, в опытах Э. Рикке (1901 г.) масса и химический состав проводника не изменялся при прохождении тока в течении года.
Экспериментальное доказательство того, что ток в металлах создается свободными электронами, было дано в опытах Л.И. Мандельштама и Н. Д. Папалекси (1912 г., результаты не были опубликованы), а также Т. Стюарта и Р. Толмена (1916 г.). Они обнаружили, что при резкой остановке быстро вращающейся катушки в проводнике катушки возникает электрический ток, создаваемый отрицательно заряженными частицами — электронами.
- электрический ток в металлах — это направленное движением свободных электронов.
Так как электрический ток в металлах образуют свободные электроны, то проводимость металлических проводников называется электронной проводимостью.
Электрический ток в металлах возникает под действием внешнего электрического поля. На электроны проводимости, находящиеся в этом поле, действует электрическая сила, сообщающая им ускорение, направленное в сторону, противоположную вектору напряженности поля. В результате электроны приобретают некоторую добавочную скорость (ее называют дрейфовой). Эта скорость возрастает до тех пор, пока электрон не столкнется с атомом кристаллической решетки металла. При таких столкновениях электроны теряют свою избыточную кинетическую энергию, передавая ее ионам. Затем электроны снова разгоняются электрическим полем, снова тормозятся ионами и т.д. Средняя скорость дрейфа электронов очень мала, около 10 –4 м/с.
- Скорость распространения тока и скорость дрейфа не одно и то же. Скорость распространения тока равна скорости распространения электрического поля в пространстве, т.е. 3⋅10 8 м/с.
- При столкновении с ионами электроны проводимости передают часть кинетической энергии ионам, что приводит к увеличению энергии движения ионов кристаллической решетки, а, следовательно, и к нагреванию проводника.
Сопротивление металлов
Сопротивление металлов объясняется столкновениями электронов проводимости с ионами кристаллической решетки. При этом, очевидно, чем чаще происходят такие столкновения, т. е. чем меньше среднее время свободного пробега электрона между столкновениями τ, тем больше удельное сопротивление металла.
В свою очередь, время τ зависит от расстояния между ионами решетки, амплитуды их колебаний, характера взаимодействия электронов с ионами и скорости теплового движения электронов. С ростом температуры металла амплитуда колебаний ионов и скорость теплового движения электронов увеличиваются. Возрастает и число дефектов кристаллической решетки. Все это приводит к тому, что при увеличении температуры металла столкновения электронов с ионами будут происходить чаще, т.е. время τ уменьшается, а удельное сопротивление металла увеличивается.
См. так же
Зависимость сопротивления от температуры
Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления от температуры выражается линейной функцией:
\(~\rho = \rho_0 \cdot (1 + \alpha \cdot \Delta t),\)
где Δt = t - t0, t0 = 0 °C, ρ0, ρ — удельные сопротивления вещества проводника соответственно при 0 °С и t °C, α — температурный коэффициент сопротивления, измеряемый в СИ в Кельвинах в минус первой степени (К -1 ) (или °C -1 ).
- Температурный коэффициент сопротивления вещества — это величина, численно равная относительному изменению удельного сопротивления проводника при его нагревании на 1 К:
Для всех металлических проводников α > 0 и слабо изменяется с изменением температуры. Для большинства металлов в интервале температур от 0 ° до 100 °С коэффициент α изменяется от 3,3⋅10 –3 до 6,2⋅10 –3 К –1 (таблица 1). У химически чистых металлов α = 1/273 К -1 .
- Существуют специальные сплавы, сопротивление которых практически не изменяется при нагревании, например, манганин и константан. Их температурные коэффициенты сопротивления очень малы и равны соответственно 1⋅10 –5 К –1 и 5⋅10 –5 К –1 .
Температурный коэффициент сопротивления (при t от 0 °С до 100 °C)
| Вещество | α, 10 –3 °К –1 | Вещество | α, 10 –3 °К –1 |
|---|---|---|---|
| Алюминий | 4,2 | Нихром | 0,1 |
| Вольфрам | 4,8 | Олово | 4,4 |
| Железо | 6,0 | Платина | 3,9 |
| Золото | 4,0 | Ртуть | 1,0 |
| Латунь | 0,1 | Свинец | 3,7 |
| Магний | 3,9 | Серебро | 4,1 |
| Медь | 4,3 | Сталь | 4,0 |
| Никель | 6,5 | Цинк | 4,2 |
Если пренебречь изменением размеров металлического проводника при нагревании, то такую же линейную зависимость от температуры будет иметь и его сопротивление
\(~R_t = R_0 \cdot (1 + \alpha \cdot \Delta t) ,\)
где R0, Rt — сопротивления проводника при 0 °С и t °С.
Зависимость удельного сопротивления металлических проводников ρ от температуры t изображена на рисунке 2.

Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена. Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Сверхпроводимость
В 1911 г. голландский физик Г. Камерлинг-Оннес, изучая изменение электрического сопротивления ртути при низких температурах, обнаружил, что при температуре около 4 К (т.е. при –269 °С) удельное сопротивление скачком уменьшается (рис. 3) до нуля. Это явление Г. Камерлинг-Оннес назвал сверхпроводимостью.

Г. Камерлинг-Оннес был удостоен Нобелевской премии по физике 1913 г. «за исследования свойств вещества при низких температурах».
Сверхпроводимость наблюдается не только у чистых металлов, но и у многих химических соединений и сплавов. При этом сами элементы, входящие в состав сверхпроводящего соединения, могут и не являться сверхпроводниками. Например, NiBi, Au2Bi, PdTe, PtSb и другие.
До 1986 г. были известны сверхпроводники, обладающие этим свойством при очень низких температурах — ниже –259 °С. В 1986-1987 годах были обнаружены материалы с температурой перехода в сверхпроводящее состояние около –173 °С. Это явление получило название высокотемпературной сверхпроводимости, и для его наблюдения можно использовать вместо жидкого гелия жидкий азот.
- Wikipedia Сверхпроводимость
- Буздин А., Варламов А. Страсти по сверхпроводимости в конце тысячелетия //Квант. — 2000. — № 1. — С. 2-8.
- Мякишев Г.Я. Физика: Электродинамика //§2.6. Сверхпроводимость
Недостатки электронной теории проводимости
Несмотря на то, что электронной теории проводимости металлов объяснила ряд явлений, она имеет и свои недостатки.
- Из теории следовало, что удельное сопротивление должно быть пропорционально корню квадратному из температуры (\(~\rho \sim \sqrt T\)), между тем, согласно опыту, ρ ~ Т.
- Для того чтобы получить значения удельной электрической проводимости металла, полученных из опыта, приходится принимать среднюю длину свободного пробега электронов в сотни раз большей, чем период решетки металла. Иными словами, электрон должен проходит без соударений с ионами решетки сотни атомов.
- Данная теория не смогла объяснить причину сверхпроводимости.
Приведенные выше недостатки указывают на то, что классическая электронная теория, представляя электрон как материальную точку, подчиняющуюся законам классической механики, не учитывала некоторых специфических свойств самого электрона, которые еще не были известны к началу XX века. Эти свойства были установлены позднее при изучении строения атома, и в 1924 г. была создана новая, так называемая квантовая или волновая механика движения электронов.
А. Ток в металлах
Электрический ток в металлах
В этом листке мы приступаем к подробному изучению того, как осуществляется прохождение электрического тока в различных проводящих средах — твёрдых телах, жидкостях и газах.
Напомним, что необходимым условием возникновения тока является наличие в среде достаточно большого количества свободных зарядов, которые могут начать упорядоченное движение под действием электрического поля. Такие среды как раз и называются проводниками электрического тока.
Наиболее широко распространены металлические проводники. Поэтому начинаем мы с вопросов распространения электрического тока в металлах.
Мы много раз говорили о свободных электронах, которые являются носителями свободных зарядов в металлах. Вам хорошо известно, что электрический ток в металлическом проводнике образуется в результате направленного движения свободных электронов.
Свободные электроны
Металлы в твёрдом состоянии имеют кристаллическую структуру: расположение атомов в пространстве характеризуется периодической повторяемостью и образует геометрически правильный рисунок, называемый кристаллической решёткой.
Атомы металлов имеют небольшое число валентных электронов, расположенных на внешней электронной оболочке. Эти валентные электроны слабо связаны с ядром, и атом легко может их потерять.
Когда атомы металла занимают места в кристаллической решётке, валентные электроны покидают свои оболочки — они становятся свободными и отправляются «гулять» по всему кристаллу (а именно, свободные электроны перемещаются по внешним орбиталям соседних атомов. Эти орбитали перекрываются друг с другом вследствие близкого расположения атомов в кристаллической решётке, так что свободные электроны оказываются «общей собственностью» всего кристалла). В узлах кристаллической решётки металла остаются положительные ионы, пространство между которыми заполнено «газом» свободных электронов (рис. 1 ).
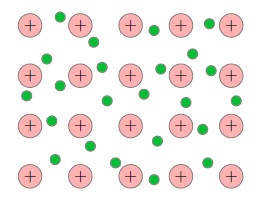
Рис. 1. Свободные электроны
Свободные электроны и впрямь ведут себя подобно частицам газа (другой адекватный образ — электронное море, которое «омывает» кристаллическую решётку) — совершая тепловое движение, они хаотически снуют туда-сюда между ионами кристаллической решётки. Суммарный заряд свободных электронов равен по модулю и противоположен по знаку общему заряду положительных ионов, поэтому металлический проводник в целом оказывается электрически нейтральным.
Газ свободных электронов является «клеем», на котором держится вся кристаллическая структура проводника. Ведь положительные ионы отталкиваются друг от друга, так что кристаллическая решётка, распираемая изнутри мощными кулоновскими силами, могла бы разлететься в разные стороны. Однако в тоже самое время ионы металла притягиваются к обволакивающему их электронному газу и, как ни в чём не бывало, остаются на своих местах, совершая лишь тепловые колебания в узлах кристаллической решётки вблизи положений равновесия.
Что произойдёт, если металлический проводник включить в замкнутую цепь, содержащую источник тока? Свободные электроны продолжают совершать хаотическое тепловое движение, но теперь — под действием возникшего внешнего электрического поля — они вдобавок начнут перемещаться упорядоченно. Это направленное течение электронного газа, накладывающееся на тепловое движение электронов, и есть электрический ток в металле (поэтому свободные электроны называются также электронами проводимости). Скорость упорядоченного движения электронов в металлическом проводнике, как нам уже известно, составляет приблизительно 0,1мм/с.
Опыт Рикке
Почему мы решили, что ток в металлах создаётся движением именно свободных электронов? Положительные ионы кристаллической решётки также испытывают на себе действие внешнего электрического поля. Может, они тоже перемещаются внутри металлического проводника и участвуют в создании тока?
Упорядоченное движение ионов означало бы постепенный перенос вещества вдоль направления электрического тока. Поэтому надо просто пропускать ток по проводнику на протяжении весьма длительного времени и посмотреть, что в итоге получится. Такого рода эксперимент и был поставлен Э.Рикке в 1901 году.
В электрическую цепь были включены три прижатых друг к другу цилиндра: два медных по краям и один алюминиевый между ними (рис. 2 ). По этой цепи пропускался электрический ток в течение года.
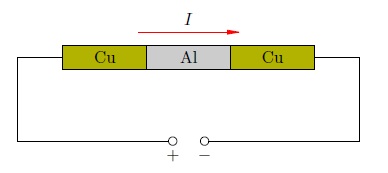
Рис. 2. Опыт Рикке
За год сквозь цилиндры прошёл заряд более трёх миллионов кулон. Предположим, что каждый атом металла теряет по одному валентному электрону, так что заряд иона равен элементарному заряду Кл. Если ток создаётся движением положительных ионов, то нетрудно подсчитать (сделайте это сами!), что такая величина прошедшего по цепи заряда соответствует переносу вдоль цепи около 2кг меди.
Однако после разъединения цилиндров было обнаружено лишь незначительное проникновение металлов друг в друга, обусловленное естественной диффузией их атомов (и не более того). Электрический ток в металлах не сопровождается переносом вещества, поэтому положительные ионы металла не принимают участия в создании тока.
Опыт Стюарта–Толмена
Прямое экспериментальное доказательство того, что электрический ток в металлах создаётся движением свободных электронов, было дано в опыте Т.Стюарта и Р.Толмена (1916 год).
Эксперименту Стюарта–Толмена предшествовали качественные наблюдения, сделанные четырьмя годами ранее русскими физиками Л.И.Мандельштамом и Н.Д.Папалекси. Они обратили внимание на так называемый электроинерционный эффект: если резко затормозить движущийся проводник, то в нём возникает кратковременный импульс тока. Эффект объясняется тем, что в течение небольшого времени после торможения проводника его свободные заряды продолжают двигаться по инерции.
Однако никаких количественных результатов Мандельштам и Папалекси не получили, и наблюдения их опубликованы не были. Честь назвать опыт своим именем принадлежит Стюарту и Толмену, которые не только наблюдали указанный электроинерционный эффект, но и произвели необходимые измерения и расчёты.
Установка Стюарта и Толмена показана на рис. 3 .
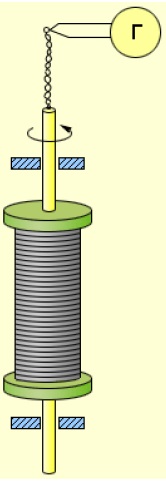
Рис. 3. Опыт Стюарта–Толмена
Катушка большим числом витков металлического провода приводилась в быстрое вращение вокруг своей оси. Концы обмотки с помощью скользящих контактов были подсоединены к специальному прибору — баллистическому гальванометру, который позволяет измерять проходящий через него заряд.
После резкого торможения катушки в цепи возникал импульс тока. Направление тока указывало на то, что он вызван движением отрицательных зарядов. Измеряя баллистическим гальванометром суммарный заряд, проходящий по цепи, Стюарт и Толмен вычислили отношение заряда одной частицы к её массе. Оно оказалось равно отношению для электрона, которое в то время уже было хорошо известно.
Так было окончательно выяснено, что носителями свободных зарядов в металлах являются свободные электроны. Как видите, этот давно и хорошо знакомый вам факт был установлен сравнительно поздно — учитывая, что металлические проводники к тому моменту уже более столетия активно использовались в самых разнообразных экcпериментах по электромагнетизму (сравните, например, с датой открытия закона Ома — 1826 год. Дело, однако, заключается в том, что сам электрон был открыт лишь в 1897 году).
Опыт показывает, что при нагревании металлического проводника его сопротивление увеличивается. Как это объяснить?
Причина проста: с повышением температуры тепловые колебания ионов кристаллической решётки становятся более интенсивными, так что число соударений свободных электронов с ионами возрастает. Чем активнее тепловое движение решётки, тем труднее электронам пробираться сквозь промежутки между ионами (Представьте себе вращающуюся проходную дверь. В каком случае труднее проскочить через неё: когда она вращается медленно или быстро? :-)). Скорость упорядоченного движения электронов уменьшается, поэтому уменьшается и сила тока (при неизменном напряжении). Это и означает увеличение сопротивления.
Как опять-таки показывает опыт, зависимость сопротивления металлического проводника от температуры с хорошей точностью является линейной:
Здесь — сопротивление проводника при . График зависимости (1) является прямой линией (рис. 4 ).
Множитель называется температурным коэффициентом сопротивления. Его значения для различных металлов и сплавов можно найти в таблицах.
Длина проводника и его площадь поперечного сечения при изменении температуры меняются несущественно. Выразим и через удельное сопротивление:
и подставим эти формулы в (1) . Получим аналогичную зависимость удельного сопротивления от температуры:
Коэффициент весьма мал (для меди, например, ), так что температурной зависимостью сопротивления металла часто можно пренебречь. Однако в ряде случаев считаться с ней приходиться. Например, вольфрамовая спираль электрической лампочки раскаляется до такой степени, что её вольт-амперная характеристика оказывается существенно нелинейной.
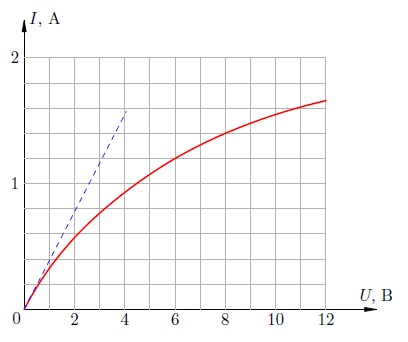
Рис. 5. Вольт-амперная характеристика лампочки
Так, на рис. 5 приведена вольт-амперная характеристика автомобильной лампочки. Если бы лампочка представляла собой идеальный резистор, её вольт-амперная характеристика была прямой линией в соответствии с законом Ома. Эта прямая изображена синим пунктиром.
Однако по мере роста напряжения, приложенного к лампочке, график отклоняется от этой прямой всё сильнее и сильнее. Почему? Дело в том, что с увеличением напряжения ток через лампочку возрастает и больше разогревает спираль; сопротивление спирали поэтому также увеличивается. Следовательно, сила тока хотя и продолжит возрастать, но будет иметь всё меньшее и меньшее значение по сравнению с тем, которое предписывается «пунктирной» линейной зависимостью тока от напряжения.
Читайте также:
