Скорость электронов в металлах и скорость света
Электронная проводимость металлов была впервые экспериментально доказана немецким физиком Э.Рикке в 1901 г. Через три плотно прижатых друг к другу отполированных цилиндра — медный, алюминиевый и снова медный — длительное время (в течение года) пропускали электрический ток. Общий заряд, прошедший за это время, был равен 3.5·10 6 Кл. Поскольку массы атомов меди и алюминия существенно отличаются друг от друга, то массы цилиндров должны были бы заметно измениться, если бы носителями заряда были ионы. Результаты опытов показали, что масса каждого из цилиндров осталась неизменной. В соприкасающихся поверхностях были обнаружены лишь незначительные следы взаимного проникновения металлов, которые не превышали результатов обычной диффузии атомов в твердых телах. Следовательно, свободными носителями заряда в металлах являются не ионы, а такие частицы, которые одинаковы и в меди, и в алюминии. Такими частицами могли быть только электроны.
Прямое и убедительное доказательство справедливости этого предположения было получено в опытах, поставленных в 1913 г. Л. И. Мандельштамом и Н. Д. Папалекси и в 1916 г. Т. Стюартом и Р. Толменом.
На катушку наматывают проволоку, концы которой припаивают к двум металлическим дискам, изолированным друг от друга (рис. 1). К концам дисков с помощью скользящих контактов присоединяют гальванометр.
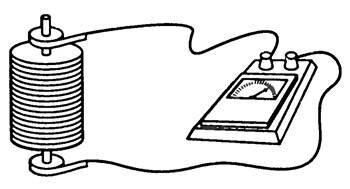
Катушку приводят в быстрое вращение, а затем резко останавливают. После резкой остановки катушки свободные заряженные частицы будут некоторое время двигаться вдоль проводника по инерции, и, следовательно, в катушке возникнет электрический ток. Ток будет существовать короткое время, так как из-за сопротивления проводника заряженные частицы тормозятся и упорядоченное движение частиц прекращается.
Направление тока говорит о том, что он создается движением отрицательно заряженных частиц. Переносимый при этом заряд пропорционален отношению заряда частиц, создающих ток, к их массе, т.е. \(~\Delta q = \frac\). Поэтому, измеряя заряд, проходящий через гальванометр за все время существования тока в цепи, удалось определить отношение \(~\frac\). Оно оказалось равным 1,8·10 11 Кл/кг. Эта величина совпадает с отношением заряда электрона к его массе, найденным ранее из других опытов.
Таким образом, электрический ток в металлах создается движением отрицательно заряженных частиц электронов. Согласно классической электронной теории проводимости металлов (П. Друде, 1900 г., Х.Лоренц, 1904 г.), металлический проводник можно рассматривать как физическую систему совокупности двух подсистем:
- свободных электронов с концентрацией ~ 10 28 м -3 и
- положительно заряженных ионов, колеблющихся около положения равновесия.
Появление свободных электронов в кристалле можно объяснить следующим образом.
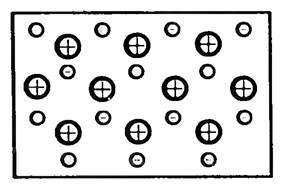
При объединении атомов в металлический кристалл слабее всего связанные с ядром атома внешние электроны отрываются от атомов (рис. 2). Поэтому в узлах кристаллической решетки металла располагаются положительные ионы, а в пространстве между ними движутся электроны, не связанные с ядрами своих атомов. Эти электроны называются свободными или электронами проводимости. Они совершают хаотическое движение, подобное движению молекул газа. Поэтому совокупность свободных электронов в металлах называют электронным газом.
Если к проводнику приложено внешнее электрическое поле, то на беспорядочное хаотическое движение свободных электронов накладывается направленное движение под действием сил электрического поля, что и порождает электрический ток. Скорость движения самих электронов в проводнике — несколько долей миллиметра в секунду, однако возникающее в проводнике электрическое поле распространяется по всей длине проводника со скоростью, близкой к скорости света в вакууме (3·10 8 м/с).
Так как электрический ток в металлах образуют свободные электроны, то проводимость металлических проводников называется электронной проводимостью.
Электроны под влиянием постоянной силы, действующей со стороны электрического поля, приобретают определенную скорость упорядоченного движения (ее называют дрейфовой). Эта скорость не увеличивается в дальнейшем со временем, так как при столкновении с ионами кристаллической решетки электроны передают кинетическую энергию, приобретенную в электрическом поле, кристаллической решетке. В первом приближении можно считать, что на длине свободного пробега λ (это расстояние, которое электрон проходит между двумя последовательными столкновениями с ионами) электрон движется с ускорением \(~a = \frac\) и его дрейфовая скорость линейно возрастает со временем\[~\upsilon = at = \frac\]. В момент столкновения электрон передает кинетическую энергию кристаллической решетке. Потом он опять ускоряется, и процесс повторяется. В результате средняя скорость упорядоченного движения электронов пропорциональна напряженности электрического поля в проводнике \(~\mathcal h \upsilon \mathcal i \sim E\) и, следовательно, разности потенциалов на концах проводника, так как \(~E = \frac Ul\), где l — длина проводника.
Известно, что сила тока в проводнике пропорциональна скорости упорядоченного движения частиц\[~I = en \mathcal h \upsilon \mathcal i S\], а значит, согласно предыдущему, сила тока пропорциональна разности потенциалов на концах проводника: I ~ U. В этом состоит качественное объяснение закона Ома на основе классической электронной теории проводимости металлов.
Однако в рамках этой теории возникли трудности. Из теории следовало, что удельное сопротивление должно быть пропорционально корню квадратному из температуры (\(~\rho \sim \sqrt T\)), между тем, согласно опыту, ρ ~ Т. Кроме того, теплоемкость металлов, согласно этой теории, должна быть значительно больше теплоемкости одноатомных кристаллов. В действительности теплоемкость металлов мало отличается от теплоемкости неметаллических кристаллов. Эти трудности были преодолены только в квантовой теории.
В 1911 г. голландский физик Г. Камерлинг-Оннес, изучая изменение электрического сопротивления ртути при низких температурах, обнаружил, что при температуре около 4 К (т.е. при -269 °С) удельное сопротивление скачком уменьшается (рис. 1) практически до нуля. Это явление обращения электрического сопротивления в нуль Г. Камерлинг-Оннес назвал сверхпроводимостью.
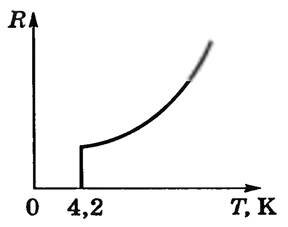
В дальнейшем было выяснено, что более 25 химических элементов — металлов при очень низких температурах становятся сверхпроводниками. У каждого из них своя критическая температура перехода в состояние с нулевым сопротивлением. Самое низкое значение ее у вольфрама — 0,012 К, самое высокое у ниобия — 9 К.
Сверхпроводимость наблюдается не только у чистых металлов, но и у многих химических соединений и сплавов. При этом сами элементы, входящие в состав сверхпроводящего соединения, могут и не являться сверхпроводниками. Например, NiBi, Au2Bi, PdTe, PtSb и другие.
Вещества в сверхпроводящем состоянии обладают необычными свойствами:
- электрический ток в сверхпроводнике может существовать длительное время без источника тока;
- внутри вещества в сверхпроводящем состоянии нельзя создать магнитное поле:
- магнитное поле разрушает состояние сверхпроводимости. Сверхпроводимость — явление, объясняемое с точки зрения квантовой теории. Достаточно сложное его описание выходит за рамки школьного курса физики.
Широкому применению сверхпроводимости до недавнего времени препятствовали трудности, связанные с необходимостью охлаждения до сверхнизких температур, для чего использовался жидкий гелий. Тем не менее, несмотря на сложность оборудования, дефицитность и дороговизну гелия, с 60-х годов XX века создаются сверхпроводящие магниты без тепловых потерь в их обмотках, что сделало практически возможным получение сильных магнитных полей в сравнительно больших объемах. Именно такие магниты требуются для создания установок управляемого термоядерного синтеза с магнитным удержанием плазмы, для мощных ускорителей заряженных частиц. Сверхпроводники используются в различных измерительных приборах, прежде всего в приборах для измерения очень слабых магнитных полей с высочайшей точностью.
В настоящее время в линиях электропередачи на преодоление сопротивления проводов уходит 10 - 15 % энергии. Сверхпроводящие линии или хотя бы вводы в крупные города принесут громадную экономию. Другая область применения сверхпроводимости — транспорт.
На основе сверхпроводящих пленок создан ряд быстродействующих логических и запоминающих элементов для счетно-решающих устройств. При космических исследованиях перспективно использование сверхпроводящих соленоидов для радиационной защиты космонавтов, стыковки кораблей, их торможения и ориентации, для плазменных ракетных двигателей.
В настоящее время созданы керамические материалы, обладающие сверхпроводимостью при более высокой температуре — свыше 100 К, то есть при температуре выше температуры кипения азота. Возможность охлаждать сверхпроводники жидким азотом, который имеет на порядок более высокую теплоту парообразования, существенно упрощает и удешевляет все криогенное оборудование, обещает огромный экономический эффект.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 279-282.
Скорость электронов в металлах и скорость света
Если атом теряет хоть один электрон, он теряет свою электронную стабильность. Теперь суммарный положительный заряд всех протонов в ядре по абсолютному значению больше отрицательного заряда электронов. Такой атом называют положительным ионом.
В таком строении кроется ответ на вопрос: “Почему в обычных условиях металл электрически нейтрален?”.
Отрицательный заряд всех свободных электронов по абсолютному значению равен положительному заряду всех ионов решетки.
Обратите внимание на тот факт, что не все электроны в металлах являются свободными. Часть из них остается связанными с ядрами атомов, а другая их часть — беспорядочно движется между этими атомами.
Эти электроны изначально находятся на самых удаленных от ядра орбитах. Они слабо связаны с ядром. Поэтому они могут довольно легко переходить от одного атома к другому, повторяя этот процесс множество раз. Именно это движение мы и называем беспорядочным движением свободных электронов.
Ток в металлах
Создадим в металле электрическое поле с помощью любого источника тока. Положительные ионы останутся в узлах кристаллической решетки. В движение придут именно свободные электроны под действием электрических сил. Их движение станет направленным (рисунок 2).
При этом сохранится и беспорядочность этого движения. Как это можно представить? Вообразите себе стайку мошкары, где каждое насекомое беспорядочно двигается. Если подует ветер, то эта стайка начнет перемещаться в одном направлении, при этом беспорядочное движение внутри этой стайки сохранится. На это и будет похоже движение электронов под действием электрических сил.
Теперь мы можем определить природу электрического тока в металлах и дать ему определение.
Электрический ток в металлах — это упорядоченное движение свободных электронов.
Доказательные опыты
Сделанные нами выводы построены не просто на рассуждениях, но и множество раз доказаны эмпирически. Российские ученые Леонид Исаакович Мандельштам (рисунок 3) и Николай Дмитриевич Папалекси (рисунок 4) провели ряд интересных опытов. Эти опыты позже были подтверждены американскими физиками Бальфуром Стюартом и Робертом Толменом.

Рисунок 3. Леонид Исаакович Мандельштам (1879 — 1944) — российский и советский физик, один из основателей научной школы радиофизики

Рисунок 4. Николай Дмитриевич Папалекси (1880 — 1947) — российский и советский физик, основоположник радиоастрономии
Суть опытов заключалась в следующем. Уже известно, что в металле есть какие-то свободные заряды, и они обладают массой. Тогда они должны испытывать на себе инерцию.
Для проверки этого предположения металлический проводник нужно было привести в движение, а затем резко остановить. Для удобства использовали вращательно движение, а не поступательное.
Металлическую проволоку наматывали на деревянный каркас и раскручивали (рисунок 5). После резкой остановки с помощью гальванометра фиксировали возникновение тока.
Было определено, что именно электроны вылетали из проводника. Установили это, определяя отношение заряда к массе его носителя. Эти данные для электрона у ученых уже имелись.
Скорость распространения электрического поля и тока в металлах
После создания электрического поля свободные электроны приходят в движение. Скорость их движения совсем небольшая. В среднем она составляет несколько миллиметров в секунду.
Но как тогда после щелчка выключателем лампа в комнате загорается мгновенно? Дело обстоит в следующем.
Именно само электрическое поле распространяется в проводнике с огромной скоростью. Она близка к скорости света в вакууме ($c = 300 \space 000 \frac$). Распространяется поле по всей длине проводника.
Соответственно, в движение приходят одновременно все электроны в проводнике. И те, что ближе к выключателю, и те, что ближе к электроприбору.
Например, пошлем электрический сигнал из Владивостока в Москву. Расстояние между этими городами составляет около 8000 км. В Москве сигнал будет зафиксирован уже через 0,03 с. Это не означает, что электроны от Владивостока проделали весь этот путь за указанное время и прибыли в Москву. Нет, это электрическое поле распространилось по проводам с невероятной скоростью и привело в движение самые ближние к приемнику в Москве электроны в движение, которое и было зафиксировано.
Поэтому, когда говорят о скорости распространения тока в проводнике, то имеется в виду скорость распространения электрического поля по всей длине проводника.
Скорость движения электронов в металлах
С какой скоростью все же двигаются сами электроны в металлах? Давайте ответим на этот вопрос и сравним полученную скорость со скоростью света, т.е. со скоростью распространения электрического поля по проводнику.
Скорость движения электронов при действии на них электрических сил называется дрейфовой скоростью.
Величина дрейфовой скорости электронов лежит в пределах $0.6 — 6 \frac$.
Сравним среднее значение этой скорости ($2.7 \frac$) со скоростью света. Для этого переведем значение, выраженное в $\frac$ в $\frac$:
$\upsilon_e = 2.7 \frac = 2.7 \cdot 10^ \frac$.
Получается, что скорость распространения электрического поля по проводнику (скорость света) больше в $10^$ раз скорости движения электронов под действием этого же электрического поля.
Kvant. Ток в металле
Этот вопрос обычно не вызывает затруднений у школьников. Как протекает? Да очень просто. Если между концам проводника, например металлического, поддерживать разность потенциалов, то в нем возникает электрическое поле. Действуя на имеющиеся в металле свободные электроны, это поле придает им ускорение в направлении того конца проводчика, потенциал которого выше (заряд электронов отрицательный). Возникает направленное движение зарядов, которое и является электрическим током.
Нельзя сказать, что такой ответ ошибочен. Все слова в нем верны. Однако этот, на первый взгляд исчерпывающий ответ сразу же вызывает целый ряд других вопросов и возражений. Попробуем и них разобраться.
Как движутся электроны при создании между концами проводника разности потенциалов? Казалось бы, ускоренно, ведь на них все время действует сила \( \vec F = e \cdot \vec E\) (\( \vec E\) – напряженность электрического поля в проводнике). Но, с другой стороны, если бы это действительно было так, то сила тока в любом сечении проводника со временем возрастала бы, что противоречит закону Ома – при постоянном напряжении сила тока, протекающего по проводнику, постоянна\[I = \dfrac \] . Как же быть? Вспомним о внутреннем устройстве металла.
Валентные электроны атомов металлов связаны с атомами весьма слабо. Поэтому при образовании кристаллической решетки они легко отрываются от атомов к образуют довольно плотный электронный газ (даже если от каждого атома оторвется лишь по одному электрону, то их концентрация в таком газе окажется порядка n ~ 10 29 м 3 , в чем вы можете убедиться самостоятельно). Рассуждая выше о протекании тока через металл, мы считали эти электроны свободными. В определенном смысле это верно, но не следует забывать и об их окружении – ионной кристаллической решетке.
Созданная в конце XIX – начале XX веков классическая электронная теория сопротивления металлов предполагала, что в процессе движения под действием электрического поля электроны сталкиваются с ионами кристаллической решетки. Среди этих столкновения бывают и такие, при которых электроны всю приобретенную при разгоне в электрическом поле энергию передают решетке. Именно такие столкновения, их называют эффективными, и ответственны за сопротивление металла. Остальные столкновения для понимания механизма протекания тока можно не принимать в расчет (после них изменяется лишь направление скорости электронов, но не ее величина).
Пусть среднее время между соударениями есть τ. Тогда можно представить себе следующую модель движения электрона в металле, в котором создано электрическое поле. В интервале времени от 0 до τ электрон движется с ускорением \( \vec a = \dfrac \), и, следовательно, проекция скорости его направленного движения против поля \( \vec E\) линейно возрастает со временем\[ \upsilon = a \cdot t = \dfrac \]. В момент времени τ электрон сталкивается с ионом и полностью передает кинетическую энергию своего направленного движения решетке. Далее он снова ускоряется электрическим полем, и процесс повторяется. График зависимости проекции скорости упорядоченного движения от времени приведен на рисунке 1.
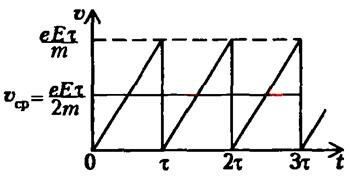
Такое кусочно-равноускоренное движение можно представить себе как равномерный дрейф электрона в направлении, противоположном полю, со скоростью \( \upsilon_ = \dfrac \). Вычислим связанную с этим движением силу тока.
Число электронов, проходящих через сечение S проводника за время Δt, есть \( \Delta N = n \cdot S \cdot \upsilon_ \cdot \Delta t\). При этом перекосится заряд \( \Delta q = e \cdot \Delta N = n \cdot e \cdot S \cdot \upsilon_ \cdot \Delta t\). Следовательно, в проводнике протекает ток
\( I = \dfrac = n \cdot e \cdot S \cdot \upsilon_ = n \cdot S \cdot \dfrac \cdot E \).
Величина \( j = \dfrac = \dfrac \cdot E\). называется плотностью тока.
Оказывается, полученный нами коэффициент при напряженности поля Е, который составлен только из микроскопических характеристик металла, есть не что иное, как величина, обратная удельному сопротивлению металла ρ.
Ну вот, кое-что стало проясняться. Однако вопросы еще остались. Давайте, например, оценим среднюю скорость направленного движения электронов. Пусть по медному проводнику сечением, скажем 10 мм 2 и концентрацией электронов n = 1,67∙10 29 м -3 протекает ток I = 10 А. Тогда средняя скорость
Если же по известному из эксперимента значению ρ определить время между эффективными соударениями, то окажется, что τ ~ 10 -14 с. Поэтому, если предполагать, что пробег между эффективными соударениями происходит со средней скоростью υcp ~ 0,1 мм/с, то мы приходим к абсурдному утверждению: расстояние между двумя соударениями электрона составляет \(l = \upsilon_ \cdot \tau \sim \) 10 -18 м, что на много порядков меньше расстояния: между ближайшими нонами в решетке. Следовательно, мы снова чего-то не учли.
А не учли мы того, что частицы электронного газа в металле, подобно молекулам идеального газа в сосуде, находятся в постоянном хаотическом движении. Однако, если воспользоваться такой аналогией и вместо υcp подставить в выражение для l тепловую скорость \(\upsilon_ = \sqrt>\), то этого все равно окажется недостаточно для согласия с опытными данными (убедитесь в этом самостоятельно).
Мы исчерпали возможности классической физики. В действительности последовательная теория сопротивления металлов была построена только в середине XX века с помощью представлений квантовой физики. Оказалось, что электроны в металле движутся с гигантскими скоростями υe ~ 0,01с (с – скорость света в вакууме). Это хаотическое движение частиц электронного газа имеет чисто квантовое, а не тепловое происхождение – оно не прекращается даже при абсолютном нуле температуры. Но и при столь огромных скоростях хаотического движения электронов в отсутствие электрического поля средний перенос заряда через выделенное сечение проводника равен нулю. При включении электрическою поля на это хаотическое движение накладывается упорядоченный дрейф электронов против поля – как это уже было описано выше. Расстояние же между двумя последовательными соударениями определяется именно большой скоростью хаотического движения и составляет для взятого нами конкретного медного проводника несколько десятков (а может бить, даже сотен) межатомных расстояний, что уже вполне правдоподобно.
И, наконец, последняя неожиданность. Согласно законам квантовой механики, электрон в идеальной периодической кристаллической решетке двигается так, что он. никогда не сталкивается с ионами, ее образующими. А как же быть тогда со всеми нашими предыдущими умозрительными построениями? Как же тогда электроны при своем движении в кристалле передают свою энергию решетке?
Оказывается, при низких температурах электроны сталкиваются с примесными атомами и другими дефектами, всегда имеющимися а решетке реального кристалла. Устраняя их, сопротивление кристаллического металлов можно делать все меньше и меньше. При комнатных же температурах электроны в основном рассеиваются на. колебаниях решетки. Если в неподвижной решетке они еще могли «строить» свое поведение так, чтобы «обойти» все периодически повторяющиеся ионы, то когда последние совершают тепловые колебания, электроны уже никак не могут «уследить» за их хаотическим движением и неизбежно сталкиваются то с одним, то с другим.
Вот, вкратце, какие «подводные камни» встретились нам при внимательном рассмотрении, казалось бы, такого ясного вопроса.
SA. Ток в металлах
В начале XX века была создана классическая электронная теория проводимости металлов (П. Друде, 1900 г., Х.Лоренц, 1904 г.), которая дала простое и наглядное объяснение большинства электрических и тепловых свойств металлов.
Рассмотрим некоторые положения этой теории.
Свободные электроны
Металлический проводник состоит из:
1) положительно заряженных ионов, колеблющихся около положения равновесия, и
2) свободных электронов, способных перемещаться по всему объему проводника.
Таким образом, электрические свойства металлов обусловлены наличием в них свободных электронов с концентрацией порядка 10 28 м –3 , что примерно соответствует концентрации атомов. Эти электроны называются электронами проводимости. Они образуются путем отрыва от атомов металлов их валентных электронов. Такие электроны не принадлежат какому-то определенному атому и способны перемещаться по всему объему тела.
В металле в отсутствие электрического поля электроны проводимости хаотически движутся и сталкиваются, чаще всего с ионами кристаллической решетки (рис. 1). Совокупность этих электронов можно приближенно рассматривать как некий электронный газ, подчиняющийся законам идеального газа. Средняя скорость теплового движения электронов при комнатной температуре составляет примерно 10 5 м/с.
Электрический ток в металлах
Ионы кристаллической решетки металла не принимают участие в создании тока. Их перемещение при прохождении тока означало бы перенос вещества вдоль проводника, что не наблюдается. Например, в опытах Э. Рикке (1901 г.) масса и химический состав проводника не изменялся при прохождении тока в течении года.
Экспериментальное доказательство того, что ток в металлах создается свободными электронами, было дано в опытах Л.И. Мандельштама и Н. Д. Папалекси (1912 г., результаты не были опубликованы), а также Т. Стюарта и Р. Толмена (1916 г.). Они обнаружили, что при резкой остановке быстро вращающейся катушки в проводнике катушки возникает электрический ток, создаваемый отрицательно заряженными частицами — электронами.
- электрический ток в металлах — это направленное движением свободных электронов.
Так как электрический ток в металлах образуют свободные электроны, то проводимость металлических проводников называется электронной проводимостью.
Электрический ток в металлах возникает под действием внешнего электрического поля. На электроны проводимости, находящиеся в этом поле, действует электрическая сила, сообщающая им ускорение, направленное в сторону, противоположную вектору напряженности поля. В результате электроны приобретают некоторую добавочную скорость (ее называют дрейфовой). Эта скорость возрастает до тех пор, пока электрон не столкнется с атомом кристаллической решетки металла. При таких столкновениях электроны теряют свою избыточную кинетическую энергию, передавая ее ионам. Затем электроны снова разгоняются электрическим полем, снова тормозятся ионами и т.д. Средняя скорость дрейфа электронов очень мала, около 10 –4 м/с.
- Скорость распространения тока и скорость дрейфа не одно и то же. Скорость распространения тока равна скорости распространения электрического поля в пространстве, т.е. 3⋅10 8 м/с.
- При столкновении с ионами электроны проводимости передают часть кинетической энергии ионам, что приводит к увеличению энергии движения ионов кристаллической решетки, а, следовательно, и к нагреванию проводника.
Сопротивление металлов
Сопротивление металлов объясняется столкновениями электронов проводимости с ионами кристаллической решетки. При этом, очевидно, чем чаще происходят такие столкновения, т. е. чем меньше среднее время свободного пробега электрона между столкновениями τ, тем больше удельное сопротивление металла.
В свою очередь, время τ зависит от расстояния между ионами решетки, амплитуды их колебаний, характера взаимодействия электронов с ионами и скорости теплового движения электронов. С ростом температуры металла амплитуда колебаний ионов и скорость теплового движения электронов увеличиваются. Возрастает и число дефектов кристаллической решетки. Все это приводит к тому, что при увеличении температуры металла столкновения электронов с ионами будут происходить чаще, т.е. время τ уменьшается, а удельное сопротивление металла увеличивается.
См. так же
Зависимость сопротивления от температуры
Опыт показывает, что при не слишком высоких и не слишком низких температурах зависимости удельного сопротивления от температуры выражается линейной функцией:
\(~\rho = \rho_0 \cdot (1 + \alpha \cdot \Delta t),\)
где Δt = t - t0, t0 = 0 °C, ρ0, ρ — удельные сопротивления вещества проводника соответственно при 0 °С и t °C, α — температурный коэффициент сопротивления, измеряемый в СИ в Кельвинах в минус первой степени (К -1 ) (или °C -1 ).
- Температурный коэффициент сопротивления вещества — это величина, численно равная относительному изменению удельного сопротивления проводника при его нагревании на 1 К:
Для всех металлических проводников α > 0 и слабо изменяется с изменением температуры. Для большинства металлов в интервале температур от 0 ° до 100 °С коэффициент α изменяется от 3,3⋅10 –3 до 6,2⋅10 –3 К –1 (таблица 1). У химически чистых металлов α = 1/273 К -1 .
- Существуют специальные сплавы, сопротивление которых практически не изменяется при нагревании, например, манганин и константан. Их температурные коэффициенты сопротивления очень малы и равны соответственно 1⋅10 –5 К –1 и 5⋅10 –5 К –1 .
Температурный коэффициент сопротивления (при t от 0 °С до 100 °C)
| Вещество | α, 10 –3 °К –1 | Вещество | α, 10 –3 °К –1 |
|---|---|---|---|
| Алюминий | 4,2 | Нихром | 0,1 |
| Вольфрам | 4,8 | Олово | 4,4 |
| Железо | 6,0 | Платина | 3,9 |
| Золото | 4,0 | Ртуть | 1,0 |
| Латунь | 0,1 | Свинец | 3,7 |
| Магний | 3,9 | Серебро | 4,1 |
| Медь | 4,3 | Сталь | 4,0 |
| Никель | 6,5 | Цинк | 4,2 |
Если пренебречь изменением размеров металлического проводника при нагревании, то такую же линейную зависимость от температуры будет иметь и его сопротивление
\(~R_t = R_0 \cdot (1 + \alpha \cdot \Delta t) ,\)
где R0, Rt — сопротивления проводника при 0 °С и t °С.
Зависимость удельного сопротивления металлических проводников ρ от температуры t изображена на рисунке 2.

Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве термометрического тела такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры достаточно изучена. Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить. Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры непригодны.
Сверхпроводимость
В 1911 г. голландский физик Г. Камерлинг-Оннес, изучая изменение электрического сопротивления ртути при низких температурах, обнаружил, что при температуре около 4 К (т.е. при –269 °С) удельное сопротивление скачком уменьшается (рис. 3) до нуля. Это явление Г. Камерлинг-Оннес назвал сверхпроводимостью.

Г. Камерлинг-Оннес был удостоен Нобелевской премии по физике 1913 г. «за исследования свойств вещества при низких температурах».
Сверхпроводимость наблюдается не только у чистых металлов, но и у многих химических соединений и сплавов. При этом сами элементы, входящие в состав сверхпроводящего соединения, могут и не являться сверхпроводниками. Например, NiBi, Au2Bi, PdTe, PtSb и другие.
До 1986 г. были известны сверхпроводники, обладающие этим свойством при очень низких температурах — ниже –259 °С. В 1986-1987 годах были обнаружены материалы с температурой перехода в сверхпроводящее состояние около –173 °С. Это явление получило название высокотемпературной сверхпроводимости, и для его наблюдения можно использовать вместо жидкого гелия жидкий азот.
- Wikipedia Сверхпроводимость
- Буздин А., Варламов А. Страсти по сверхпроводимости в конце тысячелетия //Квант. — 2000. — № 1. — С. 2-8.
- Мякишев Г.Я. Физика: Электродинамика //§2.6. Сверхпроводимость
Недостатки электронной теории проводимости
Несмотря на то, что электронной теории проводимости металлов объяснила ряд явлений, она имеет и свои недостатки.
- Из теории следовало, что удельное сопротивление должно быть пропорционально корню квадратному из температуры (\(~\rho \sim \sqrt T\)), между тем, согласно опыту, ρ ~ Т.
- Для того чтобы получить значения удельной электрической проводимости металла, полученных из опыта, приходится принимать среднюю длину свободного пробега электронов в сотни раз большей, чем период решетки металла. Иными словами, электрон должен проходит без соударений с ионами решетки сотни атомов.
- Данная теория не смогла объяснить причину сверхпроводимости.
Приведенные выше недостатки указывают на то, что классическая электронная теория, представляя электрон как материальную точку, подчиняющуюся законам классической механики, не учитывала некоторых специфических свойств самого электрона, которые еще не были известны к началу XX века. Эти свойства были установлены позднее при изучении строения атома, и в 1924 г. была создана новая, так называемая квантовая или волновая механика движения электронов.
Электрический ток в металлах

Электрическим током в физике называется согласованное (упорядоченное, однонаправленное) перемещение электрически заряженных элементарных частиц (электронов, протонов, ионов) или заряженных макроскопических частиц (например, капель дождя во время грозы). В веществах, находящихся в различных агрегатных состояниях (твердое тело, жидкость, газ) ток может формироваться из разного набора заряженных частиц. Рассмотрим механизм образования электрического тока в металлах.
Свободные электроны в металлах
Вещества, относящиеся к металлам, могут находиться как в твердом, так и в жидком состоянии (ртуть, галлий, цезий и др.). При этом все они являются проводниками электрического тока. Твердые вещества имеют структуру жесткой кристаллической решетки, в узлах которых “сидят” положительно заряженные ионы, совершающие небольшие колебания относительно точки равновесия. В объеме кристалла всегда присутствует большое количество свободных электронов, которые вырвались с орбит атомов в результате механических соударений или воздействия излучений.
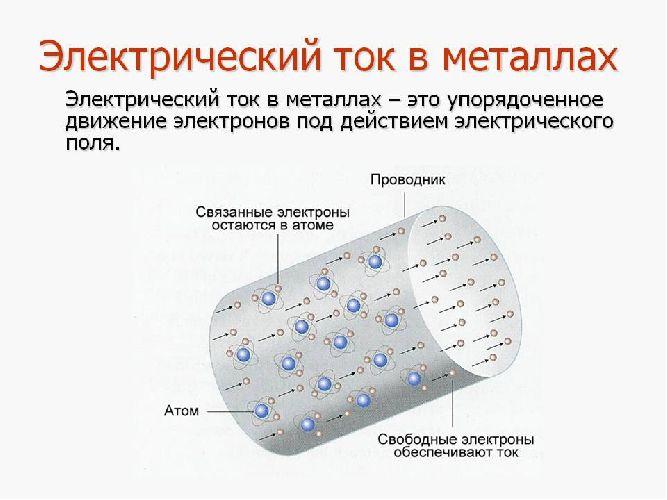
Рис. 1. Механизм электрического тока в металлах.
Это электронное “облако” движется беспорядочно, хаотично до тех пор, пока к металлу не будет приложено электрическое поле. Электрическое поле E, созданное внешним источником (батареей, аккумулятором), действует на заряд q с силой F:
Под действием этой силы электроны приобретают ускорение в одном направлении и, таким образом, появляется электрический ток в цепи.
Многочисленные наблюдения показали, что при прохождении электрического тока масса проводников и их химический состав не изменяются. Отсюда следует вывод, что ионы металлов, которые составляют основную массу вещества, не принимают участия в переносе электрического заряда.
Опыт Мандельштама и Папалекси
Электронную природу тока в металле первыми экспериментально доказали российские физики Мандельштам и Папалекси в 1913 г. Для того, чтобы выяснить, какие частицы создают электрический ток в металлах, они — без подключения внешнего источника — регистрировали ток в катушке из металлического провода, которую сначала сильно раскручивали вокруг собственной оси, а затем резко останавливали. Поскольку у электрона есть масса, то он должен подчиняться закону инерции. Поэтому в момент остановки атомы решетки останутся на месте, а свободные электроны по инерции, какое-то время, продолжат движение в прежнем направлении. То есть в цепи должен появиться электрический ток. Эксперименты подтвердил это предположение — после остановки катушки исследователи регистрировали бросок тока в цепи.
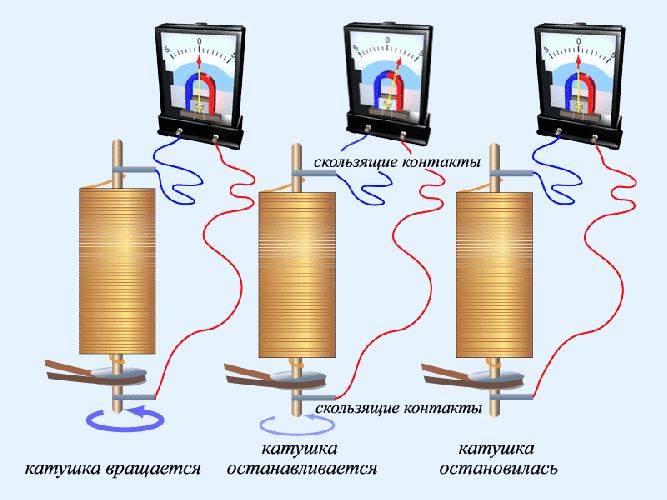
Рис. 2. Опыт Мандельштама и Папалекси.
Этот эксперимент в 1916 г. повторили американцы Стюарт и Толмен. Им удалось повысить точность измерений и получить отношение заряда электрона eэ к значению массы электрона mэ:
Этот фундаментальный результат совпал с полученными данными из других экспериментов, поставленных на основе измерения других параметров. Впервые эту величину в 1897 г. измерил англичанин Джозеф Томсон по отклонению пучка электронов в зависимости от напряженности электрического поля.
Скорость распространения электрического тока
Скорость распространения электрического поля в металле близка к скорости света в вакууме, которая равна 300000 км/с. Но это не значит, что электроны внутри вещества двигаются с такой же скоростью. Для проводника с площадью поперечного сечения S = 1 мм 2 при силе тока I = 1 A скорость упорядоченного движения электронов равна v = 6*10 -5 м/с. То есть за одну секунду электроны в проводнике за счет упорядоченного движения проходят всего 0,06 мм.
Такие малые значения скоростей движения электронов в проводниках не приводят к запаздыванию включения электрических ламп, включения бытовых приборов и т.д., так как при подаче напряжения вдоль проводов со скоростью света распространяется электрическое поле. Эта скорость настолько велика, что позволяет приводить в движение свободные электроны практически мгновенно во всех проводниках электрической цепи.
Применение свойств электрического тока в металлах
Физические свойства электрического тока используются в различных областях жизнедеятельности:
- Способность электрического тока нагревать проводники используется для изготовления нагревательных бытовых и промышленных приборов;
- Вокруг провода с электрическим током возникает магнитное поле, что позволило создать электродвигатели, без которых сегодня невозможно обойтись;
- Передача электроэнергии на различные расстояния осуществляется по проводам линий электропередачи (ЛЭП), по которым течет электрический ток.
Что мы узнали?
Итак, мы узнали, что электрический ток в металлах создается упорядоченным движением свободных электронов. Экспериментальное доказательство того, что электрический ток в металлах создают электроны, впервые получили российские физики Мандельштам и Папалекси. Физические свойства электрического тока в металлах позволили создать большое количество бытовых и промышленных устройств.
Читайте также:
