На металлической сфере радиусом 15 см находится заряд 2 нкл
Электростатика
§ 14. Напряженность электрического поля. Электрическое смещение
Условия задач и ссылки на решения на тему:
1 Электрическое поле создано двумя точечными зарядами Q1= 30 нКл Q2=-10 нКл. Расстояние между зарядами равно 20 см. Определить напряженность электрического поля в точке, находящейся на расстоянии r1=15 см от первого и на расстоянии r2=10 см от второго зарядов
РЕШЕНИЕ
2 Электрическое поле создано двумя параллельными бесконечными заряженными плоскостями с поверхностными плотностями заряда 0,4 и 0,1 мкКл/м2. Определить напряженность электрического поля, созданного этими заряженными плоскостями.
РЕШЕНИЕ
3 На пластинах плоского воздушного конденсатора находится заряд Q=10 нКл. Площадь каждой пластины конденсатора равна 100 см2. Определить силу, с которой притягиваются пластины. Поле между пластинами считать однородным
РЕШЕНИЕ
4 Электрическое поле создано бесконечной плоскостью, заряженной с поверхностной плотностью 400 нКл/м2, и бесконечной прямой нитью, заряженной с линейной плотностью τ=100 нКл/м. На расстоянии 10 см от нити находится точечный заряд Q=10 нКл. Определить силу, действующую на заряд, ее направление, если заряд и нить лежат в одной плоскости, параллельной заряженной плоскости
РЕШЕНИЕ
5 Точечный заряд Q=25 нКл находится в поле, созданном прямым бесконечным цилиндром радиусом R=1 см, равномерно заряженным с поверхностной плотностью 2 мкКл/м2. Определить силу, действующую на заряд, помещенный от оси цилиндра на расстоянии r=10 см
РЕШЕНИЕ
6 Электрическое поле создано тонкой бесконечно длинной нитью, равномерно заряженной с линейной плотностью 30 нКл/м. На расстоянии a=20 см от нити находится плоская круглая площадка радиусом r=1 см. Определить поток вектора напряженности через эту площадку, если плоскость ее составляет угол β=30° с линией напряженности, проходящей через середину площадки.
РЕШЕНИЕ
7 Две концентрические проводящие сферы радиусами R1=6 см и R2=10 см несут соответственно заряды Q1=1 нКл и Q2=-0,5 нКл. Найти напряженность поля в точках, отстоящих от центра сфер на расстояниях r1=5 см, r2=9 см и r3=15 см. Построить график E(r)
РЕШЕНИЕ
14.1 Определить напряженность электрического поля, создаваемого точечным зарядом Q=10 нКл на расстоянии r=10 см от него. Диэлектрик масло.
РЕШЕНИЕ
14.2 Расстояние между двумя точечными зарядами Q1=+8 нКл и Q2=-5,3 нКл равно 40 см. Вычислить напряженность поля в точке, лежащей посередине между зарядами. Чему равна напряженность, если второй заряд будет положительным?
РЕШЕНИЕ
14.3 Электрическое поле создано двумя точечными зарядами Q1=10 нКл и Q2=-20 нКл, находящимися на расстоянии d=20 см друг от друга. Определить напряженность поля в точке, удаленной от первого заряда на r1=30 см и от второго на r2=50 см.
РЕШЕНИЕ
14.4 Расстояние между двумя точечными положительными зарядами Q1=9Q и Q2=Q равно 8 см. На каком расстоянии r от первого заряда находится точка, в которой напряженность поля зарядов равна нулю? Где находилась бы эта точка, если бы второй заряд был отрицательным?
РЕШЕНИЕ
14.5 Два точечных заряда Q1=2Q и Q2=-Q находятся на расстоянии d друг от друга. Найти положение точки на прямой, проходящей через эти заряды, напряженность E поля в которой равна нулю
РЕШЕНИЕ
14.6 Электрическое поле создано двумя точечными зарядами Q1=40 нКл и Q2=-10 нКл, находящимися на расстоянии 10 см друг от друга. Определить напряженность поля в точке, удаленной от первого заряда на r1=12 см и от второго на r2=6 см.
РЕШЕНИЕ
14.7 Тонкое кольцо радиусом R=8 см несет заряд, равномерно распределенный с линейной плотностью т=10 нКл/м. Какова напряженность электрического поля в точке, равноудаленной от всех точек кольца на расстояние r= 10 см?
РЕШЕНИЕ
14.8 Полусфера несет заряд, равномерно распределенный с поверхностной плотностью 1 нКл/м2. Найти напряженность электрического поля в геометрическом центре полусферы.
РЕШЕНИЕ
14.9 На металлической сфере радиусом R=10 см находится заряд Q=1 нКл. Определить напряженность электрического поля в следующих точках: на расстоянии r1=8 см от центра сферы; на ее поверхности; на расстоянии r2=15 см от центра сферы. Построить график зависимости E от r.
РЕШЕНИЕ
14.10 Две концентрические металлические заряженные сферы радиусами R1=6 см и R2=10 см несут соответственно заряды Q1=1 нКл и Q2=-0,5 нКл. Найти напряженности E поля в точках, отстоящих от центра сфер на расстояниях r1=5 см, r2=9 см, r3=15 см. Построить график зависимости E(r).
РЕШЕНИЕ
14.11 Очень длинная тонкая прямая проволока несет заряд, равномерно распределенный по всей ее длине. Вычислить линейную плотность заряда, если напряженность поля на расстоянии a=0,5 м от проволоки против ее середины равна 200 В/м.
РЕШЕНИЕ
14.12 Расстояние между двумя длинными тонкими проволоками, расположенными параллельно друг другу, равно 16 см. Проволоки равномерно заряжены разноименными зарядами с линейной плотностью т=150 мкКл/м. Какова напряженность поля в точке, удаленной на r=10 см как от первой, так и от второй проволоки?
РЕШЕНИЕ
14.13 Прямой металлический стержень диаметром d=5 см и длиной 4 м несет равномерно распределенный по его поверхности заряд Q=500 нКл. Определить напряженность E поля в точке, находящейся против середины стержня на расстоянии a=1 см от его поверхности.
РЕШЕНИЕ
14.14 Бесконечно длинная тонкостенная металлическая трубка радиусом R=2 см несет равномерно распределенный по поверхности заряд 1 нКл/м2. Определить напряженность E поля в точках, отстоящих от оси трубки на расстояниях r1=1 см, r2=3 см. Построить график зависимости E(r).
РЕШЕНИЕ
14.15 Две длинные тонкостенные коаксиальные трубки радиусами R1=2 см и R2=4 см несут заряды, равномерно распределенные по длине с линейными плотностями τ1=1 τ2=-0,5 нКл/м. Пространство между трубками заполнено эбонитом. Определить напряженность E поля в точках, находящихся на расстояниях r1= 1 см, r2=3 см, r3=5 см от оси трубок. Построить график зависимости E от r.
РЕШЕНИЕ
14.16 На отрезке тонкого прямого проводника длиной 10 см равномерно распределен заряд с линейной плотностью τ=3 мкКл/м. Вычислить напряженность E, создаваемую этим зарядом в точке, расположенной на оси проводника и удаленной от ближайшего конца отрезка на расстояние, равное длине этого отрезка.
РЕШЕНИЕ
14.17 Тонкий стержень длиной l=12 см заряжен с линейной плотностью τ=200 нКл/м. Найти напряженность электрического поля в точке, находящейся на расстоянии r=5 см от стержня против его середины.
РЕШЕНИЕ
14.18 Тонкий стержень длиной l=10 см заряжен с линейной плотностью τ=400 нКл/м. Найти напряженность E электрического поля в точке, расположенной на перпендикуляре к стержню, проведенном через один из его концов, на расстоянии r=8 см от этого конца.
РЕШЕНИЕ
14.19 Электрическое поле создано зарядом тонкого равномерно заряженного стержня, изогнутого по трем сторонам квадрата. Длина стороны квадрата равна 20 см. Линейная плотность т зарядов равна 500 нКл/м. Вычислить напряженность E поля в точке A.
РЕШЕНИЕ
14.20 Два прямых тонких стержня длиной 12 см и 16 см каждый заряжены с линейной плотностью т=400 нКл/м. Стержни образуют прямой угол. Найти напряженность E поля в точке A (рис. 14.10).
РЕШЕНИЕ
14.21 Электрическое поле создано двумя бесконечными параллельными пластинами, несущими одинаковый равномерно распределенный по площади заряд 1 нКл/м2. Определить напряженность E поля между пластинами; вне пластин. Построить график изменения напряженности вдоль линии, перпендикулярной пластинам.
РЕШЕНИЕ
14.22 Электрическое поле создано двумя бесконечными параллельными пластинами, несущими равномерно распределенный по площади заряд с поверхностными плотностями 1 нКл/м2 и 3 нКл/м2. Определить напряженность E поля между пластинами; вне пластин. Построить график изменения напряженности вдоль линии, перпендикулярной пластинам.
РЕШЕНИЕ
14.23 Электрическое поле создано двумя бесконечными параллельными пластинами, несущими равномерно распределенный по площади заряд с поверхностными плотностями 2 нКл/м2 и -5 нКл/м2. Определить напряженность поля между пластинами; вне пластин. Построить график изменения напряженности вдоль линии, перпендикулярной пластинам
РЕШЕНИЕ
14.24 Две прямоугольные одинаковые параллельные пластины, длины сторон которых a=10 см и b = 15 см, расположены на малом по сравнению с линейными размерами пластин расстоянии друг от друга. На одной из пластин равномерно распределен заряд Q1 =50 нКл, на другой заряд Q2= 150 нКл. Определить напряженность электрического поля между пластинами
РЕШЕНИЕ
14.25 Две бесконечные параллельные пластины равномерно заряжены с поверхностной плотностью 10 нКл/м2 и -30 нКл/м2. Определить силу взаимодействия между пластинами, приходящуюся на площадь, равную 1 м2.
РЕШЕНИЕ
14.26 Две круглые параллельные пластины радиусом R=10 см находятся на малом по сравнению с радиусом расстоянии друг от друга. Пластинам сообщили одинаковые по модулю, но противоположные по знаку заряды Q1=Q2=Q. Определить этот заряд, если пластины притягиваются с силой F=2 мН. Считать, что заряды распределяются по пластинам равномерно.
РЕШЕНИЕ
14.27 Эбонитовый сплошной шар радиусом R=5 см несет заряд, равномерно распределенный с объемной плотностью 10 нКл/м3. Определить напряженность и смещение электрического поля в точках на расстоянии r1=3 см от центра сферы; на поверхности сферы; на расстоянии r2=10 см от центра сферы. Построить графики зависимостей E(r) и D(r).
РЕШЕНИЕ
14.28 Полый стеклянный шар несет равномерно распределенный по объему заряд. Его объемная плотность 100 нКл/м3. Внутренний радиус R1 шара равен 5 см, наружный R2=10 см. Вычислить напряженность E и смещение D электрического поля в точках, отстоящих от центра сферы на расстоянии r1=3 см; r2=6 см; r3=12 см. Построить графики зависимостей E(r) и D(r).
РЕШЕНИЕ
14.29 Длинный парафиновый цилиндр радиусом R=2 см несет заряд, равномерно распределенный по объему с объемной плотностью 10 нКл/м3. Определить напряженность E и смещение D электрического поля в точках, находящихся от оси цилиндра на расстоянии r1=1 см; r2=3 см. Обе точки равноудалены от концов цилиндра. Построить графики зависимостей E(r) и D(r).
РЕШЕНИЕ
14.30 Большая плоская пластина толщиной d=1 см несет заряд, равномерно распределенный по объему с объемной плотностью 100 нКл/м3. Найти напряженность электрического поля вблизи центральной части пластины вне ее, на малом расстоянии от поверхности.
РЕШЕНИЕ
14.31 Лист стекла толщиной d=2 см равномерно заряжен с объемной плотностью 1 мкКл/м3. Определить напряженность E и смещение D электрического поля в точках A, B, C. Построить график зависимости E(x) ось x координат перпендикулярна поверхности листа стекла
РЕШЕНИЕ
14.32 На некотором расстоянии a=5 см от бесконечной проводящей плоскости находится точечный заряд Q=1 нКл. Определить силу, действующую на заряд со стороны индуцированного им заряда на плоскости.
РЕШЕНИЕ
14.33 На расстоянии a=10 см от бесконечной проводящей плоскости находится точечный заряд Q=20 нКл. Вычислить напряженность электрического поля в точке, удаленной от плоскости на расстояние а и от заряда Q на расстояние 2а.
РЕШЕНИЕ
14.34 Точечный заряд Q=40 нКл находится на расстоянии 30 см от бесконечной проводящей плоскости. Какова напряженность E электрического поля в точке A (рис. 14.12)?
РЕШЕНИЕ
14.36 Тонкая нить несет равномерно распределенный по длине заряд с линейной плотностью τ=2 мкКл/м. Вблизи средней части нити на расстоянии r=1 см, малом по сравнению с ее длиной, находится точечный заряд Q=0,1 мкКл. Определить силу F, действующую на заряд.
РЕШЕНИЕ
14.37 Большая металлическая пластина несет равномерно распределенный по поверхности заряд 10 нКл/м2. На малом расстоянии от пластины находится точечный заряд Q=100 нКл. Найти силу F, действующую на заряд.
РЕШЕНИЕ
14.38 Точечный заряд Q=1 мкКл находится вблизи большой равномерно заряженной пластины против ее середины. Вычислить поверхностную плотность заряда пластины, если на точечный заряд действует сила F=60 мН.
РЕШЕНИЕ
14.39 Между пластинами плоского конденсатора находится точечный заряд Q=30 нКл. Поле конденсатора действует на заряд с силой F1=10 мН. Определить силу F2 взаимного притяжения пластин, если площадь 5 каждой пластины равна 100 см2.
РЕШЕНИЕ
14.40 Параллельно бесконечной пластине, несущей заряд, равномерно распределенный по площади с поверхностной плотностью 20 нКл/м2. расположена тонкая нить с равномерно распределенным по длине зарядом (т=0,4 нКл/м). Определить силу F, действующую на отрезок нити длиной ℓ=1 м.
РЕШЕНИЕ
14.41 Две одинаковые круглые пластины площадью по 100 см2 каждая расположены параллельно друг другу. Заряд Q1 одной пластины равен +100 нКл, другой Q2=-100 нКл. Определить силу F взаимного притяжения пластин в двух случаях, когда расстояние между ними: 1) r1=2 см; 2) r2=10 м.
РЕШЕНИЕ
14.42 Плоский конденсатор состоит из двух пластин, разделенных стеклом. Какое давление производят пластины на стекло перед пробоем, если напряженность E электрического поля перед пробоем равна 30 МВ/м?
РЕШЕНИЕ
14.43 Две параллельные, бесконечно длинные прямые нити несут заряд, равномерно распределенный по длине с линейными плотностями τ1=0,1 мкКл/м и τ2=0,2 мкКл/м. Определить силу взаимодействия, приходящуюся на отрезок нити длиной 1 м. Расстояние между нитями равно 10 см.
РЕШЕНИЕ
14.44 Прямая, бесконечная, тонкая нить несет равномерно распределенный по длине заряд 1 мкКл/м. В плоскости, содержащей нить, перпендикулярно нити находится тонкий стержень длиной l. Ближайший к нити конец стержня находится на расстоянии l от нее. Определить силу , действующую на стержень, если он заряжен с линейной плотностью τ2=0,1 мкКл/м.
РЕШЕНИЕ
14.45 Металлический шар имеет заряд Q1=0,1 мкКл. На расстоянии, равном радиусу шара, от его поверхности находится конец нити, вытянутой вдоль силовой линии. Нить несет равномерно распределенный по длине заряд Q2= 10 нКл. Длина нити равна радиусу шара. Определить силу F, действующую на нить, если радиус шара равен 10 см.
РЕШЕНИЕ
14.46 Соосно с бесконечной прямой равномерно заряженной линией 0,5 мкКл/м расположено полукольцо с равномерно распределенным зарядом 20 нКл/м. Определить силу F взаимодействия нити с полукольцом.
РЕШЕНИЕ
14.47 Бесконечная прямая нить несет равномерно распределенный заряд с линейной плотностью τ1=1 мкКл/м. Соосно с нитью расположено тонкое кольцо, заряженное равномерно с линейной плотностью τ2=10 нКл/м. Определить силу, растягивающую кольцо. Взаимодействием между отдельными элементами кольца пренебречь.
РЕШЕНИЕ
14.48 Две бесконечно длинные равномерно заряженные тонкие нити τ1=τ2=τ=1 мкКл/м скрещены под прямым углом друг к другу. Определить силу их взаимодействия.
РЕШЕНИЕ
14.49 Бесконечная плоскость несет заряд, равномерно распределенный с поверхностной плотностью 1 мкКл/м2. На некотором расстоянии от плоскости параллельно ей расположен круг радиусом r = 10 см. Вычислить поток ФЕ вектора напряженности через этот круг.
РЕШЕНИЕ
14.50 Плоская квадратная пластина со стороной длиной a, равной 10 см, находится на некотором расстоянии от бесконечной равномерно заряженной 1 мкКл/м2 плоскости. Плоскость пластины составляет угол 30 с линиями поля. Найти поток электрического смещения через эту пластину.
РЕШЕНИЕ
14.51 В центре сферы радиусом R=20 см находится точечный заряд Q=10 нКл. Определить поток вектора напряженности через часть сферической поверхности площадью S=20 см2
РЕШЕНИЕ
14.52 В вершине конуса с телесным углом 0,5 ср находится точечный заряд Q=30 нКл. Вычислить поток электрического смещения через площадку, ограниченную линией пересечения поверхности конуса с любой другой поверхностью.
РЕШЕНИЕ
14.53 Прямоугольная плоская площадка со сторонами, длины а и b которых равны 3 и 2 см соответственно, находится на расстоянии R= 1 м от точечного заряда Q=1 мкКл. Площадка ориентирована так, что линии напряженности составляют угол 30 с ее поверхностью. Найти поток вектора напряженности через площадку
РЕШЕНИЕ
14.54 Электрическое поле создано точечным зарядом Q=0,1 мкКл. Определить поток электрического смещения через круглую площадку радиусом R =30 см. Заряд равноудален от краев площадки и находится на расстоянии a=40 см от ее центра
РЕШЕНИЕ
14.55 Заряд Q=1 мкКл равноудален от краев круглой площадки на расстоянии r=20 см. Радиус площадки равен 12 см. Определить среднее значение напряженности E в пределах площадки
РЕШЕНИЕ
14.56 Электрическое поле создано бесконечной прямой равномерно заряженной линией 0,3 мкКл/м. Определить поток электрического смещения через прямоугольную площадку, две большие стороны которой параллельны заряженной линии и одинаково удалены от нее на расстояние r=20 см. Стороны площадки имеют размеры a=20 см, b=40 см
РЕШЕНИЕ
Электромагнетизм
Основной характеристикой магнитного поля является индукция . Величина и направление вектора индукции магнитного поля, созданного элементом проводника с током , определяются с помощью закона Био-Савара-Лапласа
где – индукция магнитного поля в точке, заданной радиус-вектором , проведенным от элемента проводника до этой точки;
– векторное произведение векторов и ;
– магнитная постоянная, – магнитная проницаемость среды.
В скалярном виде закон Био-Савара-Лапласа:
, где – угол между векторами и .
Если имеется несколько источников магнитного поля, то, согласно принципу суперпозициимагнитных полей, индукция результирующего магнитного поля равна векторной сумме индукций всех отдельных магнитных полей, т.е.
Модуль вектора поля, созданного прямолинейным бесконечным проводником с током силой I, в произвольной точке М на расстоянии r от проводника:
Сила Лоренца. На заряд q , движущейся со скоростью в магнитном поле с индукцией действует сила ( – сила Лоренца).
Модуль вектора : Fл = q v B sin α , где α – угол между векторами и .
Направление вектора может быть определено по правилу левой руки для движущихся положительных зарядов и по правилу правой руки для движущихся отрицательных зарядов (если силовые линии магнитного поля входят в ладонь, а четыре вытянутых пальца располагаются по скорости движения частицы, то отведённый большой палец укажет направление силы Лоренца).
Магнитный поток. Элементарный магнитный поток dΦ вектора индукции через элементарную площадку dS :
где – вектор, модуль которого равен площади площадки dS , а направление совпадает с направлением вектора нормали к площадке dS .
Магнитный поток Φ вектора магнитной индукции через площадку S:
Явление электромагнитной индукции – это явление возникновения ЭДС (электродвижущей силы) εi в проводящем контуре при изменении магнитного потока Φ, пронизывающего данный контур.
Абсолютная величина ЭДС электромагнитной индукции εi в проводящем контуре прямо пропорциональна величине скорости изменения магнитного потока Φ, пронизывающего данный контур:
(закон Фарадея с учётом правила Ленца).
Знак " − " в приведенной формуле отражает правило Ленца: индукционный ток в проводящей рамке имеет такое направление, что создаваемое этим током магнитное поле препятствует изменению магнитного потока, вызывающему индукционный ток в рамке.
Примеры решения задач по теме «Электростатика и электромагнетизм»
(Номера задач в скобках соответствуют сборнику задач по курсу физики Трофимовой Т.И.)
Задача № 1 (3.10.) Расстояние l между зарядами Q =± 2 нКл равно 20 см. Определите напряжённость поля, созданного этими зарядами в точке, находящейся на расстоянии r1 = 15 см от первого и r2 = 10 см от второго заряда.
Дано: l = 20 см (0,2 м); Q1 = 2 нКл ( 2· 10 -9 Кл); Q2 = – 2 нКл (– 2 · 10 -9 Кл); r1 = 15 см (0,15 м); r2 = 10 см (0,1 м).
Определить Е.
Решение. Согласно принципу суперпозиции, (направления векторов показаны на рисунке). Напряжённости электрического поля, создаваемые в вакууме зарядами Q1 и Q2,
Модуль вектора можно определить по теореме косинусов:
Подставив (1) в формулу (2), найдём искомую напряжённость в точке А:
Ответ: 2,14 кВ/м.
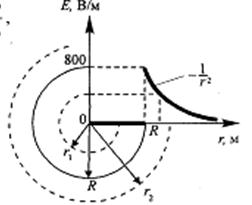
Задача № 2 (3.17.) На металлической сфере радиусом 15 см находится заряд Q = 2 нКл. Определите напряжённость электростатического поля 1) на расстоянии r1 = 10 см от центра сферы; 2) на поверхности сферы; 3) на расстоянии r2 = 20 см от центра сферы. Постройте график зависимости E(r).
Дано: R =15см (0,15 м); Q =2 нКл (2 ·10 -9 Кл); r1 =10 см (0,1 м); r2 =20 см (0,2 м).
Согласно теореме Гаусса поток вектора напряжённости электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключённых внутри этой поверхности зарядов, деленной на :
где Q – общий заряд, охватываемый произвольной поверхностью S.
Благодаря равномерному распределению заряда по поверхности сферы, поле, создаваемое ею, будет центрально-симметричным, т.е. направление вектора в любой точке проходит через центр сферы (рис.), а напряжённость есть функция расстояния r от центра сферы. При такой конфигурации поля в качестве произвольной замкнутой поверхности удобно выбрать сферу, концентрическую с заряженной сферой. Из соображений симметрии для всех точек такой поверхности .
1) r1 < R. В данном случае замкнутая поверхность радиусом r1 < Rне охватывает зарядов (рис.), поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует: Е1 = 0.
2) r = R. В качестве замкнутой поверхности построим сферу радиусом r = R, имеющую общий центр с заряженной сферой. В этом случае внутрь поверхности попадает весь заряд, создающий рассматриваемое поле, и по теореме Гаусса:
где Q – общий заряд сферы, а – площадь поверхности сферы. Тогда искомая напряжённость
3) r2 >R. В качестве замкнутой поверхности построим сферу радиусом r2 >R (рис.), имеющую общий центр с заряженной сферой. В данном случае по теореме Гаусса,
Тогда искомая напряжённость
График зависимости E(r) представлен на рисунке.
В области r < Rнапряженность Е = 0. В области r >R напряжённость определяется формулой (1), изменяясь по закону , а в точке r = R функция E(r) терпит разрыв.
Ответ: 1) Е1 = 0; 2) Е2 = 800 В/м; 3) Е3 = 450 в/м.
Задача № 3 (3.75.) Сила тока в проводнике равномерно нарастает от I0 = 0 до I = 2 А в течение времени t = 5 с. Определите заряд, прошедший в проводнике.
Дано: I0 = 0; I = 2 А; t = 5 с
Определить Q.
Из определения силы тока следует, что электрический заряд, прошедший по проводнику, за бесконечно малый промежуток времени dt
По условию задачи сила тока равномерно нарастает, т. е. , где коэффициент пропорциональности . Тогда
Проинтегрировав выражение (1) и подставив значение k, найдём искомый заряд:
Ответ: 5 Кл.
Задача № 4 (3.120.) Определите индукцию магнитного поля в центре проволочной квадратной рамки со стороной а =15 см, если по рамке течёт ток I = 5 А.
Дано: а = 15 см (0,15 м); I = 5 А.
Определить В.
Решение. Согласно принципу суперпозиции вектор магнитной индукции в центре квадратной рамки , где – вектор индукции магнитного поля, создаваемого проводником, являющимся одной из сторон квадрата. Очевидно, (каждая из сторон создаёт в центре квадратной рамки магнитное поле одного направления). По закону Био-Савара-Лапласа
Очевидно, (рис.) и , поэтому
Ответ: 37,7 мкТл.
Задача № 5 (3.143.) Протон, ускоренный разностью потенциалов U = 0,5 кВ, влетая в однородное магнитное поле с магнитной индукцией В = 2 мТл, движется по окружности. Определите радиус этой окружности.
Дано: m = 1,67· 10 --27 кг; e = 1,6· 10 -19 Кл; U = 0,5 кВ (500 В);
В = 2 мТл (2·10 -3 Тл).
ОпределитьR.
Решение. При движении протона в магнитном поле со скоростью V на него действует сила Лоренца: ,
где α – угол между векторами и (в нашем случае α = 90˚).
Из механики известно, что постоянная сила, перпендикулярная скорости (таковой и является сила Лоренца (1)), вызывает движение по окружности. Она сообщает протону нормальное ускорение , где R – радиус окружности. По второму закону Ньютона , где .
С учётом (2) искомый радиус окружности:
Ответ: 16,1 см.
Задача № 6 (3.179.) В однородное магнитное поле с индукцией В = 0,3 Тл помещена прямоугольная рамка с подвижной стороной, длина которой l = 15 см. Определите ЭДС индукции, возникающей в рамке, если её подвижная сторона перемещается перпендикулярно линиям магнитной индукции со скоростью V = 10 м/с.
Дано: В = 0,3 Тл; l = 15 см (0,15 м); V = 10 м/с.
Определить .
Решение. При перемещении подвижной стороны рамки в направлении, указанном на рисунке, поток Ф вектора магнитной индукции возрастает, что согласно закону Фарадея приводит к возникновению ЭДС индукции:
Поток вектора магнитной индукции, сцепленный с рамкой:
Подставив выражение (2) в формулу (1) и учитывая, что величины B и l постоянные, получим:
Электростатика
21. Длинный прямой провод, расположенный в вакууме, несет заряд, равномерно распределенный по всей длине провода с линейной плотностью 2 нКл/м. Определите напряженность Е электростатического поля на расстоянии r = 1 м от провода.
22. Внутренний цилиндрический проводник длинного прямолинейного коаксиального провода радиусом R1 = 1,5 мм заряжен с линейной плотностью τ1 = 0,2 нКл/м. Внешний цилиндрический проводник этого провода радиусом R2 = 3 мм заряжен с линейной плотностью τ2 = – 0,15 нКл/м. Пространство между проводниками заполнено резиной (ε = 3). Определить напряженность электростатического поля в точках, лежащих от оси провода на расстояниях: 1) r1 = 1 мм; 2) r2 = 2 мм; 3) r3 = 5 мм.
23. Электростатическое поле создается положительно заряженной с постоянной поверхностной плотностью σ = 10 нКл/м 2 бесконечной плотностью. Какую работу надо совершить для того, чтобы перенести электрон вдоль линии напряженности с расстояния r1 = 2 см до r2 = 1 см?
24. Электростатическое поле создается положительно заряженной бесконечной нитью с постоянной линейной плотностью τ = 1 нКл/см. Какую скорость приобретет электрон, приблизившись под действием поля к нити вдоль линии напряженности с расстояния r1 = 2 см до r2 = 1 см?
25. Одинаковые заряды Q = 100 нКл расположены в вершинах квадрата со стороной a = 10 см. Определить потенциальную энергию этой системы.
26. В боровской модели атома водорода электрон движется по круговой орбите радиусом r = 52,8 пм, в центре которой находится протон. Определить: 1) скорость электрона на орбите; 2) потенциальную энергию электрона в поле ядра, выразив её в электрон-вольтах.
27. Кольцо радиусом r = 5 см из тонкой проволоки несет равномерно распределенный заряд Q = 10 нКл. Определить потенциал φ электростатического поля: 1) в центре кольца; 2) на оси, проходящей через центр кольца, в точке, удаленной на расстояние a = 10 см от центра кольца.
28. На кольце с внутренним радиусом 80 см и внешним — 1м равно распределен заряд 10 нКл. Определите потенциал в центре кольца.
29. Металлический шар радиусом 5 см несет заряд Q = 10 нКл. Оп потенциал φ электростатического поля: 1) на поверхно шара; 2) на расстоянии a = 2 см от его поверхности. Постройте график зависимости φ(r).
30. Полый шар несет на себе равномерно распределенный заряд. Определить радиус шара, если потенциал в центре шара равен φ1 = 200 В, а в точке, лежащей от его центра на расстоянии r = 50 см, φ2 = 40 В.
31. Электростатическое поле создается положительным точечным зарядом. Определить числовое значение и направление градиента потенциала этого поля, если на расстоянии r = 10 см от заряда потенциал равен φ = 100 В.
32. Электростатическое поле создается бесконечной плоскостью, заряженной равномерно с поверхностной плотностью σ = 5 нКл/м 2 Определите числовое значение и направление градиента потенциала этого поля.
33. Электростатическое поле создается бесконечной прямой нитью заряженной равномерно с линейной плотностью τ = 50 пКл/см. Определите числовое значение и направление градиента потенциала в точке на расстоянии r = 0,5 м от нити.
34. Определить линейную плотность бесконечно длинной заряженной нити, если работа сил поля по перемещению заряда Q = 1 нКл с расстояния r1 = 5 см и r2 = 2 см в направлении, перпендикулярном нити, равна 50 мкДж.
35. Электростатическое поле создается положительно заряженной бесконечной нитью Протон, двигаясь от нити под действием поля вдоль линии напряженности с расстояния r1 = 1 см до r2 = 5 см, изменил свою скорость от 1 до 10 Мм/с Определите линейную плотность заряда нити.
36. Электростатическое поле создается бесконечной плоскостью, равномерно заряженной с поверхностной плотностью сигма = 1 нКл/м 2 . Определить разность потенциалов между двумя точками этого поля, лежащими на расстоянии x1 = 20 см и x2 = 50 см от плоскости.
37. Определить поверхностную плотность зарядов на пластинах плоского слюдяного (ε = 7) конденсатора, заряженного до разности потенциалов U = 200 В, если расстояние между его пластинами равно d = 0,5 мм.
38. Электростатическое поле создается равномерно заряженной сфе поверхностью радиусом R = 10 см с общим зарядом Q = 15 нКл. Определите разность потенциалов между двумя точками этого поля, лежащими на расстояниях r1 = 5 см и r2 = 15 см от поверхности сферы.
39. Электростатическое поле создается сферой радиусом R = 5 см, равномерно заряженной с поверхностной плотностью сигма = 1 нКл/м2. Определить разность потенциалов между двумя точками поля, лежащими на расстояниях r1 = 10 см и r2 = 15 см от центра сферы.
40. Электростатическое поле создается равномерно заряженным шаром радиусом R=1 м с общим зарядом Q = 50 нКл. Определите разность потенциалов для точек, лежащих от центра шара на расстояниях 1) r1 = 1,5 м и r2 = 2 м; 2) r1'= 0,3 м и r2' = 0,8 м.
Ошибка в тексте? Выдели её мышкой и нажми
Остались рефераты, курсовые, презентации? Поделись с нами - загрузи их здесь!
1. Сила гравитационного притяжения двух водяных одинаково заряженных капель радиусами 0,1 мм уравновешивается кулоновской силой отталкивания. Определите заряд капель. Плотность воды равна 1 г/см 3 .
2. Два заряженных шарика, подвешенных на нитях одинаковой длины, опускаются в керосин плотностью 0,8 г/см 3 . Какой должна быть плотность материала шариков, чтобы угол расхождения нитей в воздухе и в керосине был один и тот же? Диэлектрическая проницаемость керосина ε = 2.
3. В вершинах равностороннего треугольника находятся одинаковые положительные заряды Q = 2 нКл. Какой отрицательный заряд Q1 необходимо поместить в центр треугольника, чтобы сила притяжения с его стороны уравновесила силы отталкивания положительных зарядов?
4. Свинцовый шарик (ρ = 11,3 г/см 3 ) диаметром 0,5 помещен в глицерин (ρ = 1,26 г/см 3 ). Определить заряд шарика, если в однородном электростатическом поле шарик оказался взвешенном в глицерине. Электростатическое поле направлено вертикально вверх, и его напряженность Е = 4 кВ/см.
5. Два точечных заряда Q1 = 4 нКл и Q2 = – 2 нКл находятся друг от друга на расстоянии 60 см. Определить напряженность Е поля в точке, лежащей посередине между зарядами. Чему равна напряженность, если второй заряд положительный?
6. Определить напряженность поля, создаваемого диполем с электрическим моментом р = 1 нКл*м на расстоянии r = 25 см от центра диполя в направлении, перпендикулярном оси диполя.
7. Определить напряженность электростатического поля в точке А, расположенной вдоль прямой, соединяющей заряды Q1 = 10 нКл и Q2 = – 8 нКл и находящейся на расстоянии r = 8 см от отрицательного заряда. Расстояние между зарядами l = 20 см.
8. На некотором расстоянии от бесконечной равномерно заряженной плоскости с поверхностной плотностью сигма = 0,1 нКл/см 2 расположена круглая пластинка. Плотность пластинки составляет с линиями напряженности угол 30°. Определить поток ФЕ вектора напряженности через эту пластинку, если её радиус r равен 15 см.
9. Определите поток ФE вектора напряженности электростатического поля через сферическую поверхность, охватывающую точечные заряды Q1 = 5 нКл и Q2= -2 нКл.
10. Расстояние l между зарядами Q = ±2 нКл равно 20 см. Определите напряженность E поля, созданного этими зарядами в точке, находящейся на расстоянии r1 = 15 см от первого и r = 10 см от второго заряда.
11. В вершинах квадрата со стороной 5 см находится одинаковые положительные заряды Q = 2 нКл. Определить напряженность электростатического поля: 1) в центре квадрата; 2) в середине одной из сторон квадрата.
12. Кольцо радиусом r = 5 см из тонкой проволоки равномерно заряжено с линейной плотностью τ = 14 нКл/м. Определить напряженность поля на оси, проходящей через центр кольца, в точке, удаленной на расстоянии a = 10 см от центра кольца.
13. Определить поверхностную плотность заряда, создающего вблизи поверхности Земли напряженность Е = 200 В/м.
14. Под действием электростатического поля равномерно заряженной бесконечной плоскости точечный заряд Q = 1 нКл переместился вдоль силовой линии на расстояние r = 1 см; при этом совершена работа 5 мкДж. Определите поверхностную плотность заряда на плоскости.
15. Электростатическое поле создается двумя бесконечными параллельными плоскостями, заряженными равномерно одноименны зарядами с поверхностной плотностью соответственно σ1 = 2 нКл/м 2 и σ2 = 4 нКл/м 2 . Определите напряженность электростатического поля: 1) меж плоскостями; 2) за пределами плоскостей. Постройте график изменения напряженности вдоль линии, перпендикулярной плоскостям.
16. Электростатическое поле создается двумя бесконечными параллельными плоскостями, заряженными равномерно разноименными зарядами с поверхностной плотностью σ1 = 1 нКл/м 2 и σ2 = 2 нКл/м 2 , Оп напряженность электростатического поля: 1) между плоскостями, 2) за пределами плоскостей. Постройте график изменения напряженности поля вдоль линии, перпендикулярной плоскостям.
17. На металлической сфере радиусом 15 см находится заряд Q = 2 нКл. Определить напряженность Е электростатического поля: 1) на расстоянии r1 = 10 см от центра сферы; 2) на поверхности сферы; 3) на расстоянии r2 = 20 см от центра сферы. Постройте график зависимости Е(r).
18. Поле создано двумя равномерно заряженными концентрическими сферами радиусами R1 = 5 см и R2 = 8 см. Заряды сфер соответственно равны Q1 = 2 нКл и Q2 = – 1 нКл. Определить напряженность электростатического поля в точке, лежащих от центра сфер на расстояниях: 1) r1 = 3 см; 2) r2 = 6 см; 3) r3 = 10 см. Построить график зависимости Е(r).
19. Шар радиусом R=10 см заряжен равномерно с объемной плотностью ρ = 10 нКл/м 3 . Определите на электростатического поля: 1) на расстоянии r1 = 5 см от центра шара; 2) на рас r2 = 15 см от центра шара. Построй зависимость E(r).
20. Фарфоровый шар радиусом R = 10 см заряжен равномерно с объемной плотностью ρ = 15 нКл/м 3 . Определить напряженность электростатического поля: 1) на расстоянии r1 =5 см от центра шара; 2) на поверхности шара; 3) на расстоянии r2 = 15 см от центра шара. Постройте график зависимости E(r). Диэлектрическая проницаемость фарфора ε = 5.
На металлической сфере радиусом 15 см находится заряд q = 2 нКл. Определить напряжённость и потенциал электростатического поля: 1) на расстоянии r1 = 10 см от центра сферы; 2) на поверхности

Готовое решение: Заказ №8798

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Физика

Дата выполнения: 29.09.2020

Цена: 227 руб.
Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
№1 Задача 456.
На металлической сфере радиусом 15 см находится заряд q = 2 нКл. Определить напряжённость и потенциал электростатического поля:
1) на расстоянии r1 = 10 см от центра сферы;
2) на поверхности сферы;
3) на расстоянии r2 = 20 см от центра сферы.
Построить графики зависимости напряжённости и потенциала от расстояния E(r) и j (r).
Решение.
Согласно теореме Гаусса, поток вектора напряжённости электрического поля через произвольную замкнутую поверхность, равен алгебраической сумме зарядов, заключённых внутри этой поверхности, делённой на электрическую постоянную:
где – проекция вектора на нормаль к поверхности;
Ф/м – электрическая постоянная.
Возьмём в качестве произвольной поверхности сферу радиуса, центр которой совпадает с центром заряженной сферы. В силу симметрии, вектор напряжённости в каждой точке поверхности будет иметь одинаковую величину и будет направлен перпендикулярно к этой поверхности. Тогда:

Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Читайте также:
