Что тяжелее металл или дерево
Меня бесят видео, где один человек спрашивает другого:
-Что тяжелее килограмм ваты или железа?
-Килограмм железа! - не подумав, выдает жертва этого тупого прикола.
-Ты что дурак? - раздается голос и свинячий смех шутника, который снимает видео. -КИЛОГРАММ ваты и железа? - переспрашивает этот юморист, - они же ВЕСЯТ одинаково!
А потом они смеются, типо какой же ты тупой, я же задал элементарный вопрос.
Эти "шутники" даже не подозревают, что кило железа действительно тяжелее чем кило ваты. Почему?!
Все очень просто, масса и вес это НЕ одно и то же. Масса - мера инертности (погуглите на досуге), а значит это не гарантирует то, что вес будет одинаковым. Да, на оба тела действует одинаковая сила тяжести, но все благополучно забывают про силу АРХИМЕДА(да прямо в воздухе). На вату действует большая сила выталкивания, чтобы иметь массу равную массе железа при маленькой плотности ваты, она должна занимать объем больший по сравнению с железом. И вот тут вступает закон Архимеда, который гласит:
***
На тело, погружённое в жидкость или газ, действует выталкивающая или подъёмная сила, равная весу объёма жидкости или газа, вытесненного частью тела, погружённой в жидкость или газ.
***
Так, мы делаем вывод:
Один килограмм железа, действительно, тяжелее килограмма ваты.
Счастья, удачи, учите физику.
в этой задаче нет условия атмосферы, соответственно, не учитываем.
Хотя и объемы уравнять недолго, металл вполне может быть в виде мочалки(стружки)
А где сказано, в какой среде проводится замер, м, физик?
Также вес тела - сила, с котрой тело давит на опору (доя самых маленьких, результирующая, которая учитывает силу Архимеда), где написано, что объекты берутся одинаковой именно массой, а не весом?
Я этой хохмой во втором классе затроллил физрука (не хотел, честно, но он так и не понял, в чём была суть).
На вату действует большая сила выталкивания, чтобы иметь массу равную массе железа при маленькой плотности ваты, она должна занимать объем больший по сравнению с железом. И вот тут вступает закон Архимеда, который гласит:
Так старался, что и сам запутался. Масса - это мера инерции тела, т.е. то как оно реагирует на импульс. А вот Ваши рассуждения относятся к ВЕСУ тела. На Луне вес тела будет отличаться от земного, в отличии от массы.
жертвы егэ.. дебил мля
"-Что тяжелее килограмм ваты или железа?"
"Да, на оба тела действует одинаковая сила тяжести"
Не забывайте ещё про неоднородность гравитационного поля, из-за которой килограмм ваты ещё немного легче килограмма железа ;)
Еще Яков Перельман разбирал это.
Бред какой-то. Тоже самое, что один километр грунтовой дороги, длиннее километра асфальтовой.
Садись, двойка.
Килограмм железа ВСЕГДА будет равен килограмму ваты, как ни крути )
Да в разных условия, может меняться объем этой ваты, как и объем железа, но килограмм любого вещества всегда будет равен килограмму другого - это же мера массы.
Касательно закона Архимеда. На объем, занимаемый ватой, он не действует. Догадайтесь почему. Наверное потому, что она воздухопроницаема? Для примера попробуйте утопить в воде цельный полый шарик и такой-же полый шарик с дырками.
Так вот, если взять куб ваты, и куб железа такой-же массы, но с откачанным из него воздухом, то вес железного куба будет даже меньше из-за той-же силы архимеда. И это при одинаковой массе.
Мои мозги со мной попрощались и улетели.

Это глобальное потепление во всем виновато

Аниме Закон Архимеда


Как записать два бита на один атом и как «утонуть вверх». Дайджест новостей науки за неделю
Подробности про отличия Neuralink Илона Маска от подобных технологий; Почему ледники Земли тают по плохому сценарию; Можно ли плавать вверх ногами как в фильме «Начало»; Что за кровавые следы нашли на Луне; И как добиться сверхплотной записи информации?
Содержание ролика:
00:28 Чем уникален Neuralink
03:09 Льды тают по наисквернейшему сценарию
05:58 Плавание вверх ногами в левитирующей жидкости
08:15 На Луне нашли окисленное железо
10:19 Ученые приблизились к сверхплотной записи информации
(все ссылки на пруфы и исследования в описании ролика на ютубе)
Естественно, вживляемые мини-проводки LINK это не первая попытка добраться до мозга.. но предыдущие технологии, мягко говоря, были более топорными. Проводки нейролинка в 10 раз тоньше человеческого волоса, они считывают происходящее в мозге с отдельных нейронов, и, в будущем научатся стимулировать их. До недавнего времени внедрить 1000 электродов в мозг было мягко скажем сложно, лучшие образцы интерфейсов мозг-компьютер работали с сотней. К тому же чем тоньше электрод, тем меньше потенциальный урон мозгу через повреждение сосудов или самой ткани мозга. Разумеется, без тонкой хирургической операции, проводимой роботом, не обойтись.
К слову, слияние человека с искусственным интеллектом - это не конечная цель Нейралинка, по словам Маска. Все это делается в первую очередь для того, чтобы человечество было способно противостоять угрозе сильного искусственного интеллекта, вырвавшегося на свободу и желающего стереть нас с лица земли.
В 2014 году были представлены несколько возможных вариантов изменения климата. И теперь ученые считают, что таяние ледников развивается по наихудшему сценарию из всех. С того момента, как спутники начали мониторить ледники в 1990ых, таяние Антарктических льдов повысило уровень мирового океана на 7мм, а таяние Гренландских льдов - почти на 11 мм. А в целом уровень океана повышается на 4 мм в год.
Что такое 4 мм? Площадь мирового океана 360 миллионов квадратных километров. Т.е., используя нехитрую математику, можно вычислить, что объем прибывающей воды - 14,5 тысяч кубических километров в год.
Если так пойдет дальше, то ближе к концу века таяние ледников поднимет уровень океана еще на 17 сантиметров, а это грозит еще 16 миллионам человек, живущих в прибрежных регионах и городах, регулярными наводнениями.
Плавание вверх ногами в левитирующей жидкости
Если достаточно плотную жидкость при стекании вниз в сосуде подвергнуть вертикальным вибрациям, то она сможет задержаться на подушке из менее плотного воздуха и буквально левитировать. Ученые задумались, а как будут вести себя объекты в таком левитирующем слое? И если на верхней поверхности они вели себя прилично, то на нижней….
Если разместить объект на нижней поверхности, он не падает вниз. Отчасти из-за того, что давление под слоем жидкости высоко, слой воздуха сжимается под тяжестью жидкости. Но и в самой жидкости при движении наверх давление уменьшается, ведь чем выше, тем меньше слой воды. Объект выталкивается вверх до достижения некой точки равновесия выталкивающей силы с гравитацией.
Окисленное железо на Луне
На спутнике Земли обнаружили настоящий кровавый минерал, гематит. На нашей планете он представлен железной рудой, оксид железа. Но вот откуда на бескислородной Луне окисленное железо? До сих в образцах Лунного грунта людям встречалось лишь металлическое железо.
Т.к. на видимой стороне Луны гематита больше, то вероятно следующее: солнечный ветер крадет кислород их верхних слоев атмосферы Земли. Луна, проходя через хвост магнитосферы планеты, перехватывает его, а он уже реагирует с железом по чуть-чуть на протяжении миллиардов лет. С другой стороны, в смысле на темной стороне, на полюсах есть некоторое количество водяного льда. А если его подогреть, например, падающим метеоритом, то он может испариться и тоже вступить в реакцию с железом.
Атомная память
Ученые нашли способ менять орбитальный момент, не влияя при этом на спин. Все благодаря эффекту Эйнштейна-Хааза. Образно, разворот орбитального момента может быть скомпенсирован, если немного повернуть кусочек металла, которому принадлежит атом.
Ранее на уровне отдельного атома такой эффект не наблюдался. Но при помощи туннельного микроскопа, манипулирующего отдельными атомами, это удалось осуществить. Для этого потребовалось, чтобы атом железа, для которого меняли орбитальный момент, не затрагивая спин, находился четко поверх одного магнитно-нейтрального атома азота.
В отдаленной перспективе эта техника даст возможность писать на один атом сразу два бита информации. Немыслимая плотность. Атомный носитель информации.

Ликбез по физике (видео)
Всем привет. Недавно я начал работу над обучающими видео, в которых разбираются задачи по физике и астрономии средне-школьного уровня. В основном, как мне кажется, это пригодится для взрослых людей, которые хотели бы вспомнить курс физики, а может быть даже восполнить некоторые белые пятна. Также этот материал, думаю, может пригодиться и вашим детям-старшеклассникам, если они проходят соответствующие темы.
Я уже лет 10 решаю подобные задачи на интернет-порталах типа otvet mail ru - просто захожу туда периодически расслабиться и пощёлкать задачи в своё удовольствие. И вот возникла идея подсобрать свой опыт в виде видеороликов, в которых последовательно, шаг за шагом, будет изложен базовый уровень физики. То есть разбор каждой новой задачи будет включать всю необходимую теорию, которая не была разобрана до сих пор, и значит последовательный просмотр этих роликов позволит, по задумке, комфортно продвигаться по материалу.
В частности, мне не очень нравится способ подачи материала в обычных учебниках физики, когда вместо того, чтобы сразу обозначить формулу и обсуждать следствия из неё, авторы предварительно целыми абзацами ходят вокруг да около (хотя, быть может, детям так проще усвоить материал, мне сложно судить). В этом смысле выдавать материал для взрослых тем и хорошо, что вы мельком знаете обо всём. Нужно лишь брать любую тему (из 8 класса или 11, неважно) и кирпич к кирпичу собирать её.
Как это у меня выходит, вы можете оценить по трём первым видео, которые готовы на текущий момент.
1) Ускоренное движение:
Основная задача: Поезд, двигаясь от остановки, прошел в течение 50 сек 200 м и достиг скорости 6 м/с. Увеличивалось или уменьшалось ускорение движения с течением времени?
Содержание: равноускоренное движение, график зависимости скорости от времени, ускорение; пройденный путь - площадь под графиком; уравнение пути при равноускоренном движении S = v0*t+a*t^2/2; путь, пройденный за заданную секунду; торможение - отрицательное ускорение; средняя скорость при равноускоренном движении; арифметическая прогрессия пройденного пути за последовательные секунды; наклон графика - производная - ускорение; оценка переменного ускорения по графику.
2) Высота геостационарной орбиты:
Содержание: суть геостационарной орбиты; 0:39 понятия массы, силы, материальной точки; вектор и скаляр; 2:40 1 закон ньютона - определение инерциальной системы отсчёта; 4:20 3 закон ньютона; 5:25 2 закон ньютона - основной закон классической механики; векторное сложение; 8:25 вывод центростремительного ускорения; 11:05 в чём измеряются углы - градусы и радианы, удобство радиан в случае малых углов; 16:30 угловая скорость; 17:00 задача на центростремительное ускорение; 18:00 килограмм-сила; 19:00 закон всемирного тяготения; 19:45 звёздные сутки; 20:55 высота геостационарной орбиты = 35790 км.
3) Закон Архимеда:
Рассказ о законе Архимеда - о сложной теме для первого года обучения физике (непонятно зачем это сделано в школьной программе). Попутно поднимаются смежные вопросы, поэтому длительность видео перевалила за полчаса.
Содержание с таймкодами: 0:30 основная задача (головоломка про погружение шаров в сосуды с водой); 1:20 гравитация, сила тяжести (без учёта центробежного ускорения) mg, ускорение свободного падения = 9.8 м/с2; 3:35 опять про килограмм-силу, про показания весов (кгс отображают в кг); 4:40 сила противодействия опоры N, понятие "вес"; 6:47 понятие "давление", единица давления Паскаль; 7:50 типичные давления окружающих предметов; 8:44 закон Паскаля (передача давления во все точки газа-жидкости); 9:25 гидравлический пресс; 10:00 жидкость в гравитационном поле; 10:28 понятие "плотность", плотность воды и прочих веществ, пересчёт кг/м3 в кг/литр и г/см3; 14:03 вывод гидростатического давления P = ρgh, не путаем давление и силу давления; 15:20 вывод закона Архимеда F = ρgV для прямоугольного параллелепипеда, обоснование для любой формы вытесненной жидкости; 17:49 формулировка закона Архимеда; 18:21 задача про уменьшение "веса" шарика при погружении в воду, понятие средней плотности; 20:59 про "невесомость" в воде и тренировки космонавтов; 21:43 атмосферное давление, столб воздуха, распределение давлений по высоте, плотность воздуха (средняя и локальная), условие использования формулы гидростатического давления для газа, задача про самолёт-опылитель; 24:30 задача по воздухоплаванию (гелиевый шар); 25:54 атмосферное давление и высота соответствующего водяного (10 м) и ртутного (760 мм) столба, проблемы поверхностных насосов с глубокими водяными скважинами; 27:50 задача на гидростатическое давление и сообщающиеся сосуды; 30:55 решение основной задачи (головоломка про сосуды и весы).
Пишите комментарии: достаточно ли понятно изложен материал, насколько актуально это очередное изобретение велосипеда (при обилии других обучающих материалов).
masterok
Есть еще вариация такого вопроса про килограмм пуха и килограмм свинца и так далее. Но вот что пишет Перельман:
Общеизвестен шуточный вопрос: что тяжелее — тонна дерева или тонна железа? Не подумавши, обыкновенно отвечают, что тонна железа тяжелее, вызывая дружный смех окружающих.
Шутники, вероятно, еще громче рассмеются, если им ответят, что тонна дерева тяжелее, чем тонна железа. Такое утверждение кажется уж ни с чем не сообразным, — и однако, строго говоря, это ответ верный!
Дело в том, что закон Архимеда применим не только к жидкостям, но и к газам. Каждое тело в воздухе “теряет” из своего веса столько, сколько весит вытесненный телом объем воздуха.
Дерево и железо тоже, конечно, теряют в воздухе часть своего веса. Чтобы получить истинные их веса, нужно потерю прибавить. Следовательно, истинный вес дерева в нашем случае равен 1 тонне + вес воздуха в объеме дерева; истинный вес железа равен 1 тонне + вес воздуха в объеме железа.
Но тонна дерева занимает гораздо больший объем, нежели тонна железа (раз в 15), поэтому истинный вес тонны дерева больше истинного веса тонны железа! Выражаясь точнее, мы должны были бы сказать: истинный вес того дерева, которое в воздухе весит тонну, больше истинного веса того железа, которое весит в воздухе также одну тонну.
Так как тонна железа занимает объем в 1/8 куб. м, а тонна дерева — около 2 куб. м, то разность в весе вытесняемого ими воздуха должна составлять около 2,5 кг.
Однако не все с ним согласны. А вы согласны ? Почитайте мнение противников …
Вот например какого мнения А. Штумпф:
Если придерживаться ложной теории классической физики, то выводы Перельмана верны.
Однако он не знал об ошибках упомянутых мной выше. Поэтому у него и получился парадокс.
Убедиться в том что он не прав очень просто.
Возьмем два одинаковых динамометра и подвесим на один кусок железа, а на другой кусок дерева как это показано на Рис.1
рис.1
Подберем грузы таким образом, чтобы оба динамометра показывали значение веса равное 1 тонне. Затем подвесим динамометры к рычажным весам.
Так как вес у динамометров одинаковый, то стрелка рычажных весов установится на нуле.
Таким образом, правильным ответом на вопрос «Что тяжелее — тонна дерева или тонна железа?», будет следующий: Вес тонны железа в точности равен весу тонны дерева.
Если бы выталкивающая сила существовала в действительности, то рычажные весы показали бы 2,5кг. К счастью этого не происходит !
Динамометр учитывает все силы действующие на тело. И если он показывает 1 тонну, то на эту тонну не могут действовать никакие другие силы.
Подробнее о том, почему не существует выталкивающей силы Архимеда, вы можете прочитать здесь «Закон Архимеда и вес тела»
Ну и еще мнение интернет-читателей:
- Просто масса тела и его вес — не одно и тоже)) И если, говоря «тяжелее» подразумевается масса объекта, то дерево и железо имеют одинаковую массу, но разный вес.
- Тонна — единица массы, которая измеряется в килограммах, вес — сила с которой тело давит на опору, измеряется в ньютонах. Архимедова сила также измеряется в ньютонах и приведенные рассуждения относятся к весу тела, т.к. речь идет о сумме двух сил, приложенных к центру масс. Масса одной тонны дерева равна массе одной тонны железа. При этом вес у них будет разный.
- мне не совсем понятна эта теория, тоесть если мы начнем мерить объем этого дерева, то надо еще и объем вытесненного воздуха померить?что за глупость? воздух отдельная составляющая, воздух содержащийся в порах дерева и так учитывается, тот что вымещен, является отдельной частью, с самим деревом никак не связанным, а если мерить вес объекта в воде? надо еще и водоизмещение прибавлять? тоесть на деле наши корабли весят в десяток раз больше? я не понимаю, мне кажется это полнейшим бредом.
- Это точно из Перельмана? Из детства помню что Перельман утверждал что тонна железа тяжелее, а не тонна дерева.
«Тяжелее» — вес, сила с которой взвешиваемое тело давит на весы, т.е. то, что покажут весы. Сила Архимеда УМЕНЬШАЕТ вес и дерево в атмосфере становится МЕНЕЕ ТЯЖЕЛЫМ, т.е. ЛЕГЧЕ. Тонна — ед. измерения массы, тонна дерева вытесняет больший обьем, и ЛЕГЧЕ тонны железа. Тонна пуха еще легче, а тонна воздужных шариков с гелием вообще покажет отрицательный вес ;-)
- перечитал внимательнее, уважаемый профессор немного начудил — взвешивает в воздухе на весах дерево и железо и называет вес в тоннах (ошибка, вес — в ньютонах), потом предлагает оценить «истинный вес», откачав воздух. Думаю, что и в атмосфере и в воде и в вакууме, всегда — вес истинный, в определении веса нет условия исключить сторонние силы.
- Если ты станешь под балконом, а я тебе сброшу на голову килограмм пуха, а затем килограмм железа, вот тогда почувствуешь, что тяжелее
- По условию задачи мы имеем ЧЕТКО измеренную/взвешенную тонну железа и тонну дерева. Тут уже объем не играет роли. А вот если после измерения/взвешивания переместить эти два сравниваемых объекта относительно уровня моря/точки взвешивания вертикально, то получим маааааленькое расхождение…
- фигня какая-то. нет никакого истинного веса, есть масса, а есть вес. Вес это сила давления на опору. Если ты взвешиваешь чтобы получить одинаковый вес, то масса дерева будет больше, а если берешь одинаковую масса, то вес железа будет больше. Обычно просто задачи не корректно поставлены.
- Абсолютный кошмар — из-за жуткой путаницы в терминах. Слово «масса» вообще отсутствует! После таких вот «статеек» и возникает путаница в голове.
Так все таки, Перельман ошибается или нет ?
А теперь немного подробностей про другого знаменитого Перельмана.
Вот например на вопрос, почему Перельман отказался от миллиона за доказательство теоремы Пуанкаре, он ответил:
«Я знаю, как управлять Вселенной. И скажите — зачем же мне бежать за миллионом?»
Фрагменты интервью
- Григорий Яковлевич, еще школьником вы представляли СССР на математической олимпиаде в Будапеште. И взяли золотую медаль…
- Готовясь к олимпиаде, мы пытались решать задачи, где непременным условием было умение абстрактно мыслить. В этом отвлечении от математической логики и был главный смысл ежедневных тренировок. Чтобы найти правильное решение, необходимо было представить себе «кусочек мира».
- Не сложновато для школьников?
- Если говорить об условных и безусловных рефлексах, младенец с рождения познает мир. Если можно тренировать руки и ноги, то почему нельзя тренировать мозг?
- А не припомните ли какую-нибудь задачу той поры, казавшуюся неразрешимой?
- Неразрешимой… Пожалуй, нет. Труднорешаемой. Так точнее. Помните библейскую легенду о том, как Иисус Христос ходил по воде, аки посуху. Так вот мне нужно было рассчитать, с какой скоростью он должен был двигаться по водам, чтобы не провалиться.
- Вычисления оказались верными?
- Ну если легенда до сих пор существует, значит, и я не ошибся. Здесь нет никакой особой загадки. Благодаря нашим учителям мы уже достаточно хорошо изучили топологию – науку, позволяющую понять свойства пространства и оперировать формулами, понимая их прикладное значение, что помогает добиваться быстрых и точных результатов. Кстати, я тогда не считал победу на олимпиаде каким-то знаковым событием – это был всего лишь один из многих этапов познания в любимой науке.
Мог стать музыкантом
- А вы знаете, что мне пришлось поломать голову, выбирая профессию?
- Я имел право без экзаменов поступать в любое учебное заведение Советского Союза. Вот и колебался между мехматом и консерваторией. Выбрал математику… Мне сейчас очень интересно вспоминать студенческие годы. Мы так много успевали тогда… Процесс познания захватывал… Мы забывали о днях недели и времени года.
- В двадцать с небольшим лет вы сказали новое слово в науке…
- Никаких слов я не говорил… Просто продолжал исследовать проблемы изучения свойств трехмерного пространства Вселенной. Это очень интересно.
- Пытались объять необъятное?
- Совершенно верно… Только ведь любое необъятное тоже объятно. Диссертацию писал под руководством академика Александрова. Тема была несложной: «Седловидные поверхности в евклидовой геометрии». Можете представить себе в бесконечности равновеликие и неравномерно удаленные друг от друга поверхности? Нам нужно измерить «впадины» между ними.
- Это уже практика. По какой орбите полетит космический корабль к созвездию Псов? Какие препятствия встретит на своем пути… Хотите еще проще? Стоит ли косить сено между тремя холмами? Сколько людей и машин для этого надо? Министерство сельского хозяйства, оказывается, ни к чему. Есть формула. Пользуйся. Считай. И никакие кризисы тебе не страшны.
- А не схоластика ли это?
- Это колесо, топор, молот, наковальня – все что угодно, но только не схоластика. Давайте разберемся. Особенности современной математики заключаются в том, что она изучает искусственно изобретенные объекты. Нет в природе многомерных пространств, нет групп, полей и колец, свойства которых усиленно изучают математики. И если в технике постоянно создаются новые аппараты, всевозможные устройства, то и в математике создаются их аналоги – логические приемы для аналитиков в любой области науки. И всякая математическая теория, если она строгая, рано или поздно находит применение. К примеру, многие поколения математиков и философов пытались аксиоматизировать философию. В результате этих попыток была создана теория булевых функций, названных по имени ирландского математика и философа Джорджа Буля. Эта теория стала ядром кибернетики и общей теории управления, которые вместе с достижениями других наук привели к созданию компьютеров, современных морских, воздушных и космических кораблей. Таких примеров история математики
дает десятки.
- Значит, каждая ваша теоретическая разработка имеет прикладное значение?
- Значит, «бодрые» «жизнеутверждающие» доклады «пионеров» этой отрасли…
- Абсолютная чепуха и бессмыслица. Попытка построить дом на песке… Я научился вычислять пустоты, вместе с моими коллегами мы познаем механизмы заполнения социальных и экономических «пустот». Пустоты есть везде. Их можно вычислять, и это дает большие возможности… Я знаю, как управлять Вселенной. И скажите – зачем же мне бежать за миллионом?!
КСТАТИ
За что еще дадут миллион долларов…
В 1998 году на средства миллиардера Лэндона Клея (Landon T. Clay) в Кембридже (США) был основан Математический институт его имени (Clay Mathematics Institute) для популяризации математики. 24 мая 2000 года эксперты института выбрали семь самых, по их мнению, головоломных проблем. И назначили по миллиону долларов за каждую.
1. Проблема Кука
Нужно определить: может ли проверка правильности решения какой-либо задачи быть более длительной, чем получение самого решения. Эта логическая задача важна для специалистов по криптографии — шифрованию данных.
2. Гипотеза Римана
Существуют так называемые простые числа, например, 2, 3, 5, 7 и т. д., которые делятся только сами на себя. Сколько их всего, не известно. Риман полагал, что это можно определить и найти закономерность их распределения. Кто найдет — тоже окажет услугу криптографии.
3. Гипотеза Берча и Свиннертон-Дайера
Проблема связана с решением уравнений с тремя неизвестными, возведенными в степени. Нужно придумать, как их решать, независимо от сложности.
4. Гипотеза Ходжа
В ХХ веке математики открыли метод исследования формы сложных объектов. Идея в том, чтобы использовать вместо самого объекта простые «кирпичики», которые склеиваются между собой и образуют его подобие. Нужно доказать, что такое допустимо всегда.
5. Уравнения Навье – Стокса
О них стоит вспомнить в самолете. Уравнения описывают воздушные потоки, которые удерживают его в воздухе. Сейчас уравнения решают приблизительно, по приблизительным формулам. Нужно найти точные и доказать, что в трехмерном пространстве существует решение уравнений, которое всегда верно.
6. Уравнения Янга – Миллса
В мире физики есть гипотеза: если элементарная частица обладает массой, то существует и ее нижний предел. Но какой — не понятно. Нужно до него добраться. Это, пожалуй, самая сложная задачка. Для ее решения необходимо создать «теорию всего» — уравнения, объединяющие все силы и взаимодействия в природе. Тот, кто сумеет, наверняка получит и Нобелевскую премию.
Вот и почитайте еще про Волшебные ЧЕТЫРЕ ЧЕТВЕРКИ, про Парадокс Монти Холла и действительно ли Великая теорема Ферма доказана ?
Почему истинный вес тонны дерева больше тонны железа?
Общеизвестен шуточный вопрос: что тяжелее – тонна дерева или тонна железа? Не подумавши, обыкновенно отвечают, что тонна железа тяжелее, вызывая дружный смех окружающих.
Шутники, вероятно, еще громче рассмеются, если им ответят, что тонна дерева тяжелее, чем тонна железа. Такое утверждение кажется уж ни с чем не сообразным, – и однако, строго говоря, это ответ верный!
Дело в том, что закон Архимеда применим не только к жидкостям, но и к газам. Каждое тело в воздухе “теряет” из своего веса столько, сколько весит вытесненный телом объем воздуха.
Дерево и железо тоже, конечно, теряют в воздухе часть своего веса. Чтобы получить истинные их веса, нужно потерю прибавить. Следовательно, истинный вес дерева в нашем случае равен 1 тонне + вес воздуха в объеме дерева; истинный вес железа равен 1 тонне + вес воздуха в объеме железа.
Но тонна дерева занимает гораздо больший объем, нежели тонна железа (раз в 15), поэтому истинный вес тонны дерева больше истинного веса тонны железа! Выражаясь точнее, мы должны были бы сказать: истинный вес того дерева, которое в воздухе весит тонну, больше истинного веса того железа, которое весит в воздухе также одну тонну.
Так как тонна железа занимает объем в 1/8 куб. м, а тонна дерева – около 2 куб. м, то разность в весе вытесняемого ими воздуха должна составлять около 2,5 кг. Вот насколько тонна дерева в действительности тяжелее тонны железа!
Яков Исидорович Перельман — “Занимательная физика. Книга 1
Спасибо,поностальгировала. Достала Я.И. Перельмана "Занимательную арифметику",сижу листаю. Гениальный человек.
фигня какая-то. нет никакого истинного веса, есть масса, а есть вес. Вес это сила давления на опору. Если ты взвешиваешь чтобы получить одинаковый вес, то масса дерева будет больше, а если берешь одинаковую масса, то вес железа будет больше. Обычно просто задачи не корректно поставлены.
Правда ли, что наркоз отнимает пять лет жизни?
Распространено мнение, что каждый наркоз забирает у человека пять лет жизни. Мы решили проверить, подтверждается ли это научными исследованиями.
(Спойлер для ЛЛ: нет)
Контекст. Информацию о таком вреде наркоза можно найти на многих сайтах и форумах. Этот же вопрос пациенты регулярно задают врачам. О распространённости этого убеждения свидетельствует также народное творчество, в частности расхожий анекдот (да, я помню Правило): «Пациент перед операцией спрашивает анестезиолога: "Правда ли, что наркоз отнимает пять лет жизни у пациента и отдаёт их анестезиологу?". Анестезиолог отвечает: "Я уже 140 лет живу, но о таком слышу впервые"».
В обиходе наркозом часто называют любой вид анестезии — например, говорят «лечить зубы под наркозом», имея при этом в виду местную анестезию. При этом наркоз — это искусственное обратимое состояние угнетения центральной нервной системы, при котором возникает сон, потеря сознания, расслабление скелетных мышц, снижение или отключение некоторых рефлексов, а также пропадает болевая чувствительность. То есть под наркозом человек условно спит, а под другим типом анестезии остаётся в сознании. С местной (регионарной) анестезией сталкиваются многие — во время лечения и имплантации зубов или лазерной коррекции зрения. К регионарной анестезии также относится эпидуральная анестезия, позволяющая при нахождении пациента в сознании провести операцию кесарева сечения или обезболить роды. Под регионарной анестезией в некоторых случаях может быть также проведено удаление аппендицита. Пациент имеет право выбора метода анестезии в тех ситуациях, когда имеются различные варианты.
Есть также ещё один тип технология, позволяющая проводить операции, — седация. При некоторых видах седации пациент остаётся в сознании, самостоятельно дышит, может выполнить простые команды врача, но при этом спокоен и расслаблен, находится в дремотном состоянии и с большой долей вероятности не запомнит происходящее в деталях.
Так как в большинстве утверждений речь идёт только о наркозе как таковом, то и в тексте мы будет рассматривать только его влияние на продолжительность жизни. Для начала обратимся к обычной логике. Идея о том, что наркоз отнимает у человека пять лет жизни, подразумевает, что заранее известно, сколько проживёт человек. Однако такую цифру, даже проведя все самые новейшие диагностические процедуры, вывести нельзя. Различные скрининги могут помочь диагностировать заболевания в ранней стадии или определить те, к которым человек более склонен в силу семейного анамнеза или образа жизни. Например, в ситуации, когда старшие родственники женщины умерли от рака молочной железы, врач может заподозрить мутацию в генах BRCA1 и BRCA2 и предложить соответствующее наблюдение или даже превентивное оперативное вмешательство, однако высчитать возраст смерти этой женщины он никак не сможет.
Второй довод против такого убеждения тоже построен на логике. Некоторые люди добровольно переносят огромное количество пластических операций (допустим, что часть из них была не под наркозом, а под местной анестезией). Например, американка Синди Джексон, внесённая в Книгу Гиннесса, перенесла 47 косметических процедур, 14 из которых были пластическими операциями, а значит, требовали наркоза. Посчитаем: если бы каждый наркоз забирал у неё пять лет жизни, суммарно она должна была «лишиться» 70 лет. В 2022 году ей исполнилось 66 лет. То есть суммарно без операций она должна была бы прожить 136 лет и повторно войти в Книгу Гиннеса, побив предыдущий рекорд долгожительства (122 года).
Также долгожителями-рекордсменами должны были оказаться и звёзды. Например, певица Шер, по подсчётам зарубежных журналистов, перенесла не менее 60 операций (сама она отрицает это количество). То есть наркозы забрали бы у неё целых 300 лет, что с её нынешним возрастом в 76 лет бьёт все мыслимые и немыслимые рекорды!
Интересно в контексте такого убеждения о наркозе рассмотреть перспективы оперативного вмешательства у пожилых людей. По логике утверждения об отнимающем годы жизни наркозе, те из них, кому было отведено прожить после операции менее пяти лет, должны поголовно умирать на операционном столе и не выходить из наркоза. Даже, видимо, в том случае, если причиной их смерти должна была стать, например, автомобильная авария, «запланированная» через год после операции под наркозом.
Научные данные также опровергают взаимосвязь наркоза с сокращением жизни. На людях сравнительных исследований не проводили в силу их неэтичности, однако есть эксперименты на животных. Исследователи из Медицинской школы Гарварда разделили 16 крыс в возрасте 22 месяца (средний возраст жизни животных два, два с половиной года) на две группы: одним дали наркоз продолжительностью два часа, другие наркоза не получили. Крысы из контрольной группы прожили в среднем ещё 140 дней (около четырёх с половиной месяцев), а крысы, перенёсшие анестезию, — 158 дней (чуть больше пяти месяцев).
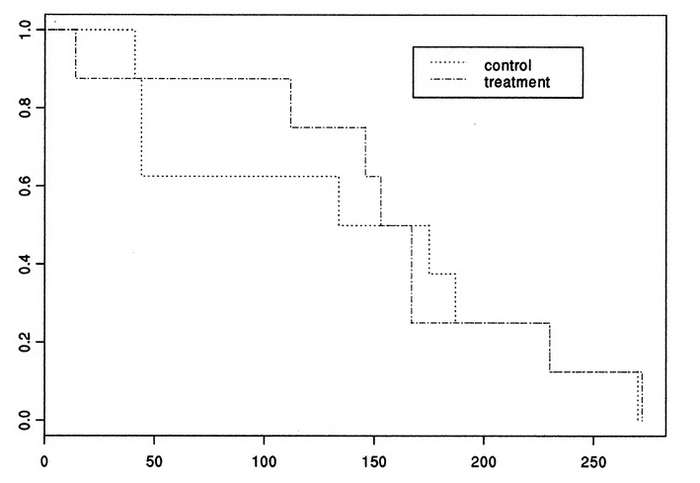
График продолжительности жизни крыс после вмешательства. Источник
Учёные даже отметили «тенденцию к увеличению продолжительности жизни крыс, которая ранее была анестезирована». Исследователи также отметили: отдельные наблюдения демонстрируют, что люди, перенёсшие операцию под наркозом в пожилом возрасте, действительно зачастую умирают раньше своих сверстников. Однако выводы на основании них о вреде анестезии делать нельзя. Ведь эти люди оказались под наркозом не ради исследования его эффектов, а из-за соответствующих патологий здоровья, которые, по всей видимости, и стали причиной того, что они умирали раньше своих сверстников.
Более того, в большинстве случаев, за исключением, пожалуй, только пластических операций, наркоз пациенту дают, чтобы провести необходимое оперативное вмешательство и спасти жизнь. Например, если не прооперировать человека, попавшего в серьёзное ДТП, то во многих случаях он просто не выживет. Также операция под наркозом для онкобольных может существенно продлить жизнь или улучшить её качество.
Таким образом, наркоз сам по себе, судя по экспериментам на животных, не отнимает годы жизни. Более того, убеждение об отнятых годах противоречит и обычной логике. Однако те, кто подвергся оперативному вмешательству, действительно могут умереть раньше своих сверстников, но не из-за наркоза, а из-за той болезни, которая и потребовала операции.
Ошибка Перельмана или "что тяжелее - тонна дерева или тонна железа" ?

Общеизвестен шуточный вопрос: что тяжелее — тонна дерева или тонна железа? Не подумавши, обыкновенно отвечают, что тонна железа тяжелее, вызывая дружный смех окружающих.
Шутники, вероятно, еще громче рассмеются, если им ответят, что тонна дерева тяжелее, чем тонна железа. Такое утверждение кажется уж ни с чем не сообразным, — и однако, строго говоря, это ответ верный!
Но тонна дерева занимает гораздо больший объем, нежели тонна железа (раз в 15), поэтому истинный вес тонны дерева больше истинного веса тонны железа! Выражаясь точнее, мы должны были бы сказать: истинный вес того дерева, которое в воздухе весит тонну, больше истинного веса того железа, которое весит в воздухе также одну тонну.
Так как тонна железа занимает объем в 1/8 куб. м, а тонна дерева — около 2 куб. м, то разность в весе вытесняемого ими воздуха должна составлять около 2,5 кг.
Если придерживаться ложной теории классической физики, то выводы Перельмана верны. Однако он не знал об ошибках упомянутых мной выше. Поэтому у него и получился парадокс. Убедиться в том что он не прав очень просто. Возьмем два одинаковых динамометра и подвесим на один кусок железа, а на другой кусок дерева как это показано на рисунке ниже:

Подберем грузы таким образом, чтобы оба динамометра показывали значение веса равное 1 тонне. Затем подвесим динамометры к рычажным весам.
Так как вес у динамометров одинаковый, то стрелка рычажных весов установится на нуле.
Таким образом, правильным ответом на вопрос «Что тяжелее — тонна дерева или тонна железа?», будет следующий: Вес тонны железа в точности равен весу тонны дерева.
Если бы выталкивающая сила существовала в действительности, то рычажные весы показали бы 2,5кг. К счастью этого не происходит !
Динамометр учитывает все силы действующие на тело. И если он показывает 1 тонну, то на эту тонну не могут действовать никакие другие силы.

- мне не совсем понятна эта теория, то есть если мы начнем мерить объем этого дерева, то надо еще и объем вытесненного воздуха померить?что за глупость? воздух отдельная составляющая, воздух содержащийся в порах дерева и так учитывается, тот что вымещен, является отдельной частью, с самим деревом никак не связанным, а если мерить вес объекта в воде? надо еще и водоизмещение прибавлять? то есть на деле наши корабли весят в десяток раз больше? я не понимаю, мне кажется это полнейшим бредом.
«Тяжелее» — вес, сила с которой взвешиваемое тело давит на весы, т.е. то, что покажут весы. Сила Архимеда УМЕНЬШАЕТ вес и дерево в атмосфере становится МЕНЕЕ ТЯЖЕЛЫМ, т.е. ЛЕГЧЕ. Тонна — ед. измерения массы, тонна дерева вытесняет больший объем, и ЛЕГЧЕ тонны железа. Тонна пуха еще легче, а тонна воздушных шариков с гелием вообще покажет отрицательный вес ;-)

Вот в комментах уже указали, что книгу и задачу описывал другой Перельман, не тот который отказался от миллиона. Но давайте все же немного о нем. Вот например на вопрос, почему этот (который не тот) Перельман отказался от миллиона за доказательство теоремы Пуанкаре, он ответил:
«Я знаю, как управлять Вселенной. И скажите — зачем же мне бежать за миллионом?»
Фрагменты интервью

Читайте также:
