Как связать фрактал
Традиционно в математике, пространства и множества содержат в себе точки. Однако же, суще-ствуют пространства, в которых “точки” сами являются множествами. С математической точки зрения, достоинство абстрагирования от точки состоит в достижении общности.
Пример этого – сжимающие отображения и связанные с ними теоремы сходимости. Сжимаю-щие отображения определяются в метрических пространствах как отображения уменьшающие расстояния между точками. Сжимающие отображения обладают важным свойством. Если взять любую точку и начать итеративно применять к ней одно и то же сжимающее отображение: f(f(f. f(x))), то результатом будет всегда одна и та же точка. Чем больше раз применим, тем точ-нее найдем эту точку. Называется она неподвижной точкой и для каждого сжимающего отоб-ражения она существует, причем только одна. Системы итерированных функций (IFS) являются примером применения этой теории.
1.1 Определение

Система итерированных функций это конечный набор функций Fi: X -> X в метрическом про-странстве X. Каждая из них расширяется до отображения Fi: H(X) -> H(X), где H(X) это пространство точки которого являются непустыми сжатыми подмножествами X. Если использовать Хаусдорфову метрику, то H(X) полно если X было полным. Кроме того, сжатия FiX X остаются сжатиями и на H(X). В совокупности, определяют новое сжатие F: H(X) -> H(X), по следующей формуле: для каждого A∈H(X), F(A) = ∪Fi(A). Из общей теории, для полного метрического пространства X, F имеет фиксированную точку AF: F(AF) = AF, которую можно достичь последовательными приближениями из любой начальной точки. Фиксированные точки IFS иногда называются аттракторами или инвариантами.
Рисунок 6. Пример построения треугольника Серпинского с помощью IFS.
Таким образом, возникают две задачи. Первая – это нахождение аттрактора заданной IFS. Вто-рая проблема противоположна первой: для заданного множества A∈H(X), найти IFS для которой A является аттрактором.
1.2 Детерминированный алгоритм
Первая проблема решается с помощью детерминированного алгоритма.
Начнем с множества A0∈H(X) и станем последовательно вычислять
Ak = ∪Fi(Ak-1) = F(Ak-1), k > 1. Ряд
1.3 Алгоритм случайных итераций
Математика альтернативного алгоритма – алгоритма случайных итераций, сложнее, но его при-менение проще. Сопоставим позитивные частоты pi отображениям Fi. Начнем с произвольной точки x0∈X. На каждом шаге k+1, выберем xk+1 из множества . Fj(xk) выбирается с веро-ятностью pj / pi. Последовательность[5] сходится к AF. На практике, чтобы изобразить при-ближение AF на компьютере, точки последовательности выводятся на экран. Числа никак не изменяют AF, но существенно влияют на процесс отображения его приближений.
1.4 Теорема коллажа
Обратная задача приближенно решается теоремой коллажа. Цитируя М. Барнсли: “теорема го-ворит нам, что чтобы найти IFS аттрактор которой “похож” на данное множество необходимо найти набор сжимающих отображений некоторого большего множества включающего своим подмножеством исходное множество, таких, что объединение, или коллаж, отображений этого множества аппроксимировало бы исходное множество”.
1.5 Использование
- Изображение делится на небольшие неперекрывающиеся квадратные области, называе-мые ранговыми блоками.
- Строится пул всех возможных перекрывающихся блоков в четыре раза больших ранго-вых — доменных блоков.
- Для каждого рангового блока по очереди «примеряем» доменные блоки и ищем такое преобразование, которое делает доменный блок наиболее похожим на текущий ранго-вый.
- Пара «преобразование — доменный блок», которая приблизилась к идеалу, ставится в соответствие ранговому блоку. В закодированное изображение сохраняются коэффициенты преобразования и координаты доменного блока. Содержимое доменного блока нам ни к чему — вы же помните, нам все равно с какой точки стартовать.

Декодирование же производится просто и довольно быстро. Берем любое изображение, делим на ранговые области, последовательно заменяем их результатом применения соответствующего преобразования к соответствующей доменной области (что бы она ни содержала в данный мо-мент). После нескольких итераций исходное изображение станет похоже на себя:
Рисунок 8. Пример восстановления сжатого изображения.
2. Системы Линденмайера
[3]
Красота растений привлекала внимание математиков веками. Активнее всего изучались инте-ресные геометрические свойства растений, такие как симметрия листьев относительно центральной оси, радиальная симметрия цветов, и спиральное расположение семечек в шишках. «Красота связана с симметрией» (H. Weyl. Symmetry). Во время роста живых организмов, особенно растений, можно четко видеть регулярно повторяющиеся многоклеточные структуры. В случае составных листьев, например, маленькие листочки, которые являются частью большого взрослого листа, имеют ту же форму, что весь лист имел на раннем этапе формирования.
В 1968г. Венгерский биолог и ботаник Аристид Линденмайер (Aristid Lindenmayer) предложил математическую модель для изучения развития простых многоклеточных организмов, которая позже была расширена и используется для моделирования сложных ветвящихся структур — разнообразных деревьев и цветов. Эта модель получила название Lindenmayer System, или про-сто L-System.
2.1 Основные идеи

Основная идея L-систем — постоянная перезапись (rewriting) элементов строки. О чем это? В данном случае перезапись — это способ получения сложных объектов путем замены частей простого начального объекта по некоторым правилам. Классическим примером является сне-жинка Коха. На рисунке инициатор — это начальный объект, грани которого заменяются на объект-генератор. Далее с новым объектом проделывается то же самое.
Рисунок 1. Снежинка Коха.

Возвращаясь к L-системам и проводя аналогию с фракталами, можно сказать, что L-система оперирует со строкой символов по специальным правилам, начиная с первоначальной простой аксиомы. Таким образом, L-система является математической грамматикой. Но фундаменталь-ное отличие L-систем от формальных грамматик состоит в том, что правила применяются одно-временно ко всей строке, к каждому символу, плюс, нет понятий терминальных и нетерминаль-ных символов. То есть «вывод» по этой грамматике может продолжаться бесконечно.
На следующей картинке видно соотношение между контекстно-свободными (OL), контекстно-зависимыми (IL) L-системами и другими формальными грамматиками в иерархии Хомского.
Рисунок 2. Иерархия Хомского.
2.2 Простейшие L-системы
Также, как и в классификации Хомского, L-системы имеют и свою классификацию от простых до сложных и мощных.
Самым простым примером являются детерминированные контекстно-свободные L-системы или сокращенно DOL. Я не люблю формальные определения грамматик, так что скажу просто своими словами. Есть некоторый набор символов — алфавит. Этим алфавитом записывается строка, с которой работает L-система. Есть аксиома — первоначальная строка из одной или более буквы и набор правил вида a → ab. Во время каждой итерации алгоритма, применяя правило к букве из текущей строки, она (буква) заменяется на набор букв справа от стрелки. Проще рассмотреть конкретный пример развития многоклеточного организма Anabaena catenula, который изучал Линденмайер, когда он предложил модель L-систем.
Пусть наш алфавит состоит из следующих символов, каждый из которых обозначает некоторую клетку: alar bl br.
Аксиома состоит из одного символа:
ω: ar
И четырех правил.
p1: ar → albr
p2: al → blar
p3: br → ar
p4: bl → al

Правила говорят, какие символы меняются на какие в процессе роста организма. На картинке видно как, применяя правила мы наблюдаем «деление» клеток и развитие.
Рисунок 3. L-система симулирующая развитие Anabaena catenula.
2.4 Использование LOGO
- F — продвинуться вперед и нарисовать линию
- f — продвинуться вперед ничего не рисуя
- + — повернуть влево
- — — повернуть вправо
- & — повернуть вниз
- ^ — повернуть вверх
- \ — наклониться влево
- / — наклониться вправо
- | — развернуться на 180 градусов
2.5 Растения и ветвящиеся структуры

Все, что было до этого является, в общем-то, непрерывными кривыми. Такой способ моделиро-вания не подходит для моделирования растений с их ветвящейся топологией. Для этого в алфа-вит были добавлены символы [ и ], которые обозначают начало и конец ветвления соответ-ственно. Когда черепашка встречает символ [, ее текущее состояние пишется в стек и извлекает-ся оттуда при встрече символа ]. Уже такой простой грамматикой можно сгенерировать доволь-но интересные двумерные и трехмерные объекты похожие на деревья.
Рисунок 5. Примеры ветвящихся L-систем.
2.6 Стохастические L-системы
Стохастические L-системы добавляют возможность задания вероятности выполнения того или иного правила, и в общем случае не являются детерминированными, ибо разные правила могут иметь один и тот же символ слева. Это вносит некоторый элемент случайности в получающиеся структуры.
2.7 Контекстно-зависимые L-системы
Так же, как и контекстно зависимость в формальных грамматиках, в L-системы синтаксис пра-вил усложняется и принимает во внимание окружение заменяемого символа.
2.8 Параметрические L-системы
К каждому символу добавляется параметр-переменная (возможно не одна), которая позволяет, например, указывать величину угла поворота для + и -, длину шага и толщину линии, проверять условия для применения правила, считать количество итераций и передавать «сигналы» вперед и назад. Пример параметрической L-системы.
ω: B(2)A(4, 4)
p1: A(x, y) :y p2: A(x, y) :y > 3 → B(x)A(x/y, 0)
p3: B(x) :x < 1 → C
p4: B(x) :x >= 1 → B(x − 1)
Параметрические контекстно-зависимые L-системы позволяют моделировать рост многокле-точных организмов и растений с учетом биохимических процессов и окружающей среды.
2.9 Использование
Еще в конце 80х L-системы использовались для визуализации моделей растений. Сейчас воз-можности компьютеров ушли далеко вперед. Многие игры и инструменты 3d моделирования используют процедурную генерацию контента, в том числе и L-системы. Как видите, из набора простых правил можно получить огромное количество разных растений и засадить ими целые поля.
Привет, Хабр! Сегодняшний пост про фракталы попался в рамках проработки темы Python, в частности, Matplotlib. Последуем примеру автора и предупредим, что в посте много тяжелой анимации, которая может даже не работать на мобильном устройстве. Зато как красиво.

Всем приятного чтения
Фракталы прекрасны. Они выстраиваются в соответствии с очень сложным паттерном и сохраняются без искажения при любом увеличении! В этой статье мы рассмотрим, как можно с легкостью начертить фракталы нескольких видов, воспользовавшись инструментом под названием L-Systems и модулем Turtle для Python, чтобы выполнить пошаговое вычерчивание.
В этой статье мы не будем чрезмерно вдаваться в технические детали; вместо этого я ограничусь кратким введением, покажу много анимированных примеров и код, при помощи которого вы сможете сами сгенерировать такой пример. Если желаете пропустить теорию и только посмотреть анимацию, сразу переходите к примерам. Кроме того, в конце я укажу несколько ресурсов, как по написанию кода, так и по базовой математике, которые вы, возможно, захотите исследовать.
Что такое фрактал?
Для начала давайте дадим «нестрогое» определение фрактала. В принципе, фрактал — это геометрическая фигура, демонстрирующая одни и те же свойства независимо от степени увеличения.
Это определение небезупречно, поэтому вот более точное с сайта Math World:
Фрактал – это объект или величина, демонстрирующие самоподобие (в формальном смысле) в любых масштабах. Объект демонстрирует при разных масштабах не идентичные структуры, но на всех уровнях фрактала должны проявляться структуры одного и того же «типа». В таком случае график, откладываемый в системе координат с логарифмическим масштабом, где по осям отсчитываются величина и масштаб, то график представляет собой прямую линию с наклоном, отражающим размерность фрактала. — Math World
Как чертить фракталы при помощи Python?
Как правило, отрисовка фракталов сложна, так как глубинная природа фракталов определяется концепцией рекурсии. Говоря о графиках и их вычерчивании, мы обычно считаем, что они образованы пикселями или векторами, но количество пикселей или векторов всегда ограничено, а фракталы по определению бесконечно рекурсивны. Таким образом, попытавшись нанести фрактал на координатную сетку, мы в какой-то момент должны будем остановиться, и именно поэтому мы в данном случае говорим об «итерациях». На каждой итерации фрактал становится все сложнее, и в какой-то момент становится невозможно отличить две его итерации, следующие друг за другом (такой момент наступает, когда изменения происходят на уровне, сравнимом с размером пикселя). Здесь логично остановиться, но, как правило, форма фрактала вырисовывается быстрее, и остановиться можно еще раньше.
Два подобных примера – квадратный остров Коха, чья структура четко вырисовывается после трех итераций, и дракон Картера-Хейтуэя, для построения полной структуры которого достаточно 8 итераций. Необходимое количество итераций сильно зависит от конкретного фрактала, с которым мы работаем.
Разумеется, существует множество библиотек на Python для построения графиков, среди которых наиболее популярна Matplotlib, но они обычно рассчитаны на нанесение статистических данных и вычерчивание хорошо известных графиков. В частности, Matplotlib содержит некоторые низкоуровневые конструкции, при помощи которых можно строить фракталы, но на этот раз мы сосредоточимся на незаслуженно малоизвестном модуле стандартной библиотеки, который называется Turtle.
Модуль Turtle
В документации Python читаем: «графика Turtle – популярный инструмент для первого знакомства детей с программированием. Он входил в состав оригинального языка программирования Logo, разработанного Уолли Фёрзегом и Сеймуром Пейпертом в 1966 году.»
Суть заключается в том, что черепаха по умолчанию распознает 3 команды:
- Ползти вперед
- Повернуть влево на угол
- Повернуть вправо на угол
L-система – это способ представления рекурсивных структур (например, фракталов) в виде строки символов и многократной перезаписи такой строки. Опять же, дадим формальное определение:
Система Линденмайера, также известная как L-система, это механизм перезаписи строк, который может использоваться для генерации фракталов с размерностью от 1 до 2 — Math World
Поняв, что такое L-система, мы сможем создавать рекурсивные структуры, но прежде давайте разберемся, какие компоненты нам для этого понадобятся. В каждой L-системе есть:
- Алфавит: множество символов, которые будет использовать L-система.
- Аксиома: исходная строка для генерации.
- Набор инструкций создания строк: эти инструкции описывают, как каждый символ должен заменяться на следующей итерации.
Учитывая, что мы собираемся использовать Turtle для построения графиков и L-системы для представления того, что собираемся наносить на график, нам необходимо создать взаимосвязь между ними.
Поскольку в Turtle мы располагаем только теми командами, что перечислены выше, присвоим каждой из них символ; из этих символов и будет состоять алфавит.
- F: ползти вперед
- +: повернуть вправо
- -: повернуть влево
Теперь давайте перейдем к примерам!
Анимированные примеры
Следующие примеры были взяты в Интернете из нескольких общедоступных источников, и я решил портировать их на Python при помощи модуля Turtle, центрировать их, раскрасить и предоставить способ экспорта в векторный формат.
ВНИМАНИЕ: предлагаемые анимации достаточно велики, рекомендуется смотреть их лишь с хорошим интернетом. Код Repl может не работать, так как потребляет ваши ресурсы, и с отображением фракталов на мобильных устройствах возможны проблемы.
Внимание: Skulpt использует для рендеринга и создания анимации ВАШ БРАУЗЕР, так что при подвисании, лагах или любом странном поведении обычно достаточно просто заново воспроизвести анимацию или перезагрузить страницу. На мобильном устройстве может не работать.
Примеры даны в порядке усложнения (на мой субъективный взгляд), так что самое интересное – в конце.
Под фракталами понимают фигуры, особенность которых — подобие самим себе. В рамках курсовой работы по C++ мы написали приложение, шустро отрисовывающее 3D-фракталы и позволяющее их вращать, приближать-отдалять, изменять параметры, записывать видео и не только. В этой статье расскажем, как шла разработка, с какими задачами в ходе неё мы сталкивались и как их решали.

Кто мы?
Разработкой приложения в течение пяти месяцев занимались три человека: Сергей Журавлев, Степан Константинов и Дарья Леднева — все первокурсники бакалаврской программы «Прикладная математика и информатика» петербургского кампуса НИУ ВШЭ. Менторил нас Антон @0xfe0d Соснин.
Задумка темы проекта
Понимая, что на первом году обучения ребята ещё слишком юны, руководство образовательной программы не требует от проектов первокурсников научной новизны. Это довольно сильно упрощает выбор идеи. Мы решили ничего не выдумывать и остановиться на нисколько не новой, но интересной теме — 3D-фракталах, ибо было понятно, что такой проект выйдет зрелищным и эффектным.
Немного о фракталах
Давайте чутка разберёмся, что такое фракталы, и как они задаются.
Фрактал — это фигура (множество точек), подобная своей части. Такое свойство влечет за собой довольно необычные особенности. Так, фрактал нетривиален при любом масштабе, то есть в отличие от регулярных фигур (эллипсов, тетраэдров, графиков гладких функций), которые при бесконечном приближении стремятся стать фрагментом прямой, внешний вид фракталов никак не упрощается при увеличении масштаба.
Фракталы можно задавать и строить по-разному. Одни из самых простых в построении — это фрактальные кривые. Таковой, например, является снежинка Коха. Генерируется она несложной рекурсивной процедурой.
Начнем с ломаной с тремя изломами, как на картинке (n=1), и назовем её генератором. Далее каждое звено ломаной заменим на фигуру, подобную генератору, и будем продолжать так до бесконечности.
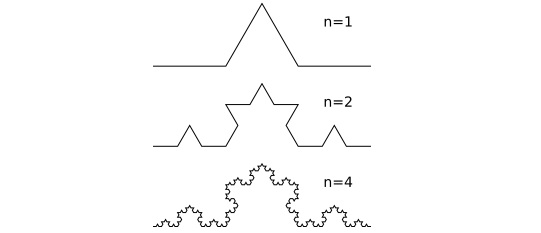
Снежинка Коха
Более интересные двухмерные фракталы можно задать, исследуя рекурсивные итерации многочлена на комплексной плоскости. Например, пусть P(z) — многочлен, а z0 — комплексное число. Тогда можно рассмотреть следующую комплексно-числовую последовательность: z0, z1=P(z0), z2=P(P(z0)), …, zn=P(zn-1), …. При стремлении n к бесконечности, такая последовательность может вести себя по-разному:
стремиться к бесконечности;
стремиться к какому-то конечному пределу;
зациклиться и не иметь предела вообще.
Цвет фрактала в каждой точке z0 пространства рассчитывается в зависимости от поведения последовательности: задается некоторая окрестность z0 и фиксированное число итераций k. Если через k итераций последовательность не вышла за пределы окрестности, точка окрашивается в черный цвет, иначе точке присваивается цвет в зависимости от номера итерации, на которой последовательность вышла за пределы окрестности.
Так, например, известный фрактал — множество Жюлиа — это множество так называемых точек бифуркации для многочлена P(z)=z 2 +c. То есть таких значений z0, при сколь угодно малых изменениях которых поведение последовательности zn может менять тип своего поведения.
Другой пример — множество Мандельброта — это все комплексные c такие, что при P(z)=z 2 +c и фиксированном z0, последовательность zn не стремится к бесконечности.
Такие способы, основанные на построении рекурсивной последовательности, легко обобщаются и на трехмерные фракталы. Для этого вместо двумерных комплексных чисел нужно использовать трехмерные гиперкомплексные числа. В нашем проекте для задания фракталов мы использовали именно этот подход.
Помимо прямого трехмерного обобщения множества Мандельброта, в проекте мы добавили возможность выбора из пяти других фракталов, всё так же основывающихся на методе рекурсивной последовательности. Все они задаются уравнением z n +c (n пользователь приложения может задать сам), но для каждого из них по-своему задана операция возведения в степень трёхмерного гиперкомплексного числа z.
Выбор технологий для UI и графики
Единственным обязательным условием, которое накладывало на курсовые работы руководство программы, было использование C++ в качестве основного языка. Ну а раз язык обязали взять классический, то и GUI библиотеку мы выбрали соответствующую — Qt.
Призадуматься нас заставил поиск технологии графической отрисовки. Самый банальный способ что-то отрисовать — двойным вложенным циклом для каждого пикселя посчитать, какого цвета он должен быть, и покрасить. Такой подход использует ресурсы исключительно CPU, причём в одном потоке. В качестве эксперимента мы попробовали реализовать именно такой способ отрисовки даже не 3D-, а 2D-фракталов. Производительность, как нетрудно предположить, была критически низкой: на разрешении FullHD кадр рендерился больше 10 секунд. Это никуда не годилось.
Спасибо нашему ментору, который развеял наши надежды на CPU-подход и чётко направил работу в сторону рендеринга силами GPU (а ведь изначально мы рассматривали идею просто оптимизировать CPU-отрисовку). Мы остановились на OpenGL. К слову, ни у кого из членов нашей команды опыта написания GPU-шейдеров не было, поэтому пришлось изучать всё с основ.
О способе рендеринга фракталов
Отрисовку фракталов мы реализовали при помощи технологии volume ray casting — про неё есть хорошая статья на Хабре. Коротко о технологии: бросаем лучи в направлении от камеры и идём по ним, пока не встретим точку, принадлежащую фракталу. Так мы получаем карту его глубин, на основе чего и отрисовываем кадр. Оттенок цвета точки фрактала будем выбирать исходя количества итераций, потребовавшихся для того, чтобы дойти до этой точки (чем отдалённее — тем светлее). Разумеется, мы устанавливаем некоторый лимит на дальность проброса луча.
Volume ray casting отлично подходит для рендеринга 3D-фрактала, ибо определять, не упёрлись ли мы в него, совсем нетрудно. Одной из альтернатив является технология volume ray tracing (трассировка лучей). Про её отличие от casting рассказано в той же статье. Выбор на именно casting пал по банальной причине: он в разы быстрее tracing’а, хоть и может уступать по качеству. Мы пробовали рисовать фракталы обоими способами, и трассировка, в отличие от бросания, работала неприемлемо медленно.
Реализованный функционал

Внешний вид программы
В нашем приложении был реализован такой функционал:
1. Выбор типа и параметров фрактала. Пользователю доступны:
выбор из шести типов фракталов;
ввод значений координат константы для уравнения фрактала zn+c;
ввод значения степени n из того же уравнения;
выбор цветового тона фрактала и фона.
выбор из шести типов фракталов;
ввод значений координат константы для уравнения фрактала z n +c;
ввод значения степени n из того же уравнения;
выбор цветового тона фрактала и фона.
По умолчанию каждому этому параметру задано рандомное значение из разумных промежутков.
2. Отрисовка фрактала.
3. Вращение, приближение-отдаление при помощи мыши.
В то время как увеличение было реализовано без лишних затруднений, реализация вращения оказалась для нас нетривиальной задачей. Правильно применить матрицу поворота в шейдере получилось по итогу длительных проб и ошибок.
4. Изменение параметров фрактала «на ходу» — фрактал рендерится вместе с движением ползунков, вводом в поля новых значений параметров.
5. Кнопка генерации случайного фрактала. Здесь мы позаботились об отсеивании слишком схожих цветов фрактала и фона.
6. Автовращение.
7. Фуллскрин.
8. Возвращение масштаба и положения камеры в исходную позицию.
9. Сохранение/загрузка текущих параметров фрактала и положения камеры в/из json-файл(а).
10. Фото- и видеосъёмка фрактала:
Изображение снимается при помощи встроенных возможностей Qt’ового класса QOpenGLWidget.
Видео сцепляется при помощи ffmpeg’а из высокочастотных снимков, сделанных вышеупомянутым способом. Разумеется, съёмка ведётся в отдельном потоке.
Итоги и много фракталов
Проект однозначно вышел интересным и в меру сложным. Если задачи, связанные с графическим интерфейсом и записью видео, представляли из себя скорее техническую работу — чтение документаций и монотонное написание кода, — то разработка, связанная с самими фракталами, несла в себе весьма содержательную математику. Как уже говорилось, одной из наиболее сложных задач было обеспечение корректного вращения фрактала.
Конечно, проект далёк от завершения. Вот лишь некоторые из направлений для дальнейшей работы:
Одна из наиболее завораживающих вещей во фракталах — это перемещение и приближение камеры в ту часть, что подобна фигуре, видимой в исходном положении камеры. Однако определение такой точки и требуемого ракурса для зума в случае с трёхмерными фракталами — крайне нетривиальная задача, и за неё мы даже не брались. Тем не менее, самоподобие наших фракталов возможно наблюдать и так.
Мы не сделали никаких метрических замеров скорости отрисовки разных конфигураций фракталов на разном железе. На данный момент все заключения о производительности были лишь умозрительными.
Типов наших фракталов пусть и несколько, но все они объединены схожим способом построения. Разумеется, существует огромное количество других подходов к заданию 3D-фракталов, коих в нашем приложении не представлено.
Степень детализации захардкожена несколькими константами в коде шейдера. Конечно, выбор уровня качества прорисовки должен быть предоставлен пользователю.
Фрактал circle Фрактал Мандельброта
Другие материалы из нашего блога о проектах студентов младших курсов:
Золотое сечение имеет большое значение для нашего восприятия мира, так как по предположению большинства ученых все в мире основано по принципу золотого сечения. Это число входит в тройку самых известных иррациональных чисел, т.е. таких чисел, десятичные представления которых бесконечны и не периодичны. Два других - это отношение длины окружности к диаметру (Пи) и основание натуральных логарифмов (е).
Золотое сечение можно встретить в повседневной жизни повсюду. Например, в древней Греции его использовали для возведения архитектурных сооружений, золотое сечение присутствует в строение человека, в искусстве, музыке и даже в строении галактики (рис.80).

Золотое сечение можно представить в виде отрезка, разделенного на два более мелких, таким образом, что длина одного (в данном случаи отрезка А) равнялась 0,382, а длина другого(отрезка В), была равна 0, 618.(рис.81)

Так, хаусдорфова размерность знаменитого канторового множества выражается в конечном виде числом: 1n2/1nЗ ≈ 0,618.(рис.82)

Рис. 82 Канторового множество - один из первых фракталов
Золотое сечение φ определяется выражением:

Если мы рассмотрим отношение А к В, где А это меньшая длина отрезка по отношении к В (рис.83), то получим обычное квадратное уравнение:
Данное выражение имеет два корня:

Обычно рассматривают только положительный корень х1, дающий простое и наглядное деление отрезка в заданной пропорции. Действительно, если принять целый отрезок за единицу, то, используя значение этого корня х1, получим а ≈ 0,382, b ≈ 0,618.
Именно положительный корень x1 уравнения наиболее часто называют золотой пропорцией или пропорцией золотого сечения. Соответствующее геометрическое деление отрезка называют золотым сечением.

Это выражение представляет собой результат решения задачи о делении целого на две неравные части так, чтобы отношение меньшей части ( А ) к большей ( В ) равнялось бы отношению большей части к целому. Действительно, соответствующая данной задаче пропорция

удовлетворяется при выполнении условия

Из определения золотого сечения (1) — (4) следует, что оно, в сущности, является двойственным объектом. Действительно, золотое сечение фактически порождается вышеупомянутой задачей о делении целого, которое представляет собой типичный пример двойственной системы, поскольку состоит из двух частей (А и В), которые, во-первых, не равны друг другу (так как А < В), во- вторых, неразрывно связаны друг с другом (как составные части целого и посредством соотношения (3)), в-третьих, взаимно дополняют друг друга (до целого, которое равно их сумме А + В) и, в-четвертых, определяют друг друга (благодаря выражению (4), позволяющему находить значение одной из величин А и В при известной другой).
С золотым сечением тесно связан числовой ряд Фибоначчи 1, 1, 2, 3, 5, 8, 13, 21. задаваемый рекуррентным соотношением:

Можно показать, что золотое сечение φ является пределом ряда

(7),
составленного из отношений соседних чисел ряда Фибоначчи, т.е.

В золотом сечении есть фигура, которая называется «Золотым прямоугольником» (рис.83). Она обладает многими необычными свойствами, которые уже знакомы нам, когда мы описывали свойства множества Мандельброта. Отрезав от "золотого" прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, "в остатке" мы снова получим "золотой" прямоугольник меньших размеров. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие "золотые" прямоугольники. Причем, располагаться они будут по логарифмической спирали, имеющей большое значение в математических моделях природных объектов (например: в завихрениях торнадо, строении ракушки и даже галактики.
Полюс спирали лежит на пересечении диагоналей начального прямоугольника BD и первого отрезаемого вертикального АС. Причем диагонали всех последующих уменьшающихся "золотых" прямоугольников лежат на этих диагоналях.

Эта логарифмическая спираль является прототипом фундаментального фрактала. В любом масштабе он подобен самому себе и остается нвариантным при большинстве геометрических преобразований.

На рис.84 изображен элемент, из которого выстраивается «Золотой прямоугольник».
Существование золотых спиралей в юлианских циклах указывает на взаимосвязь между циклами, числом пять, золотым сечением и логарифмической спиралью. И если мы желаем глубоко проникнуть в суть циклов, то следует учитывать эти фундаментальные элементы и их соотношения. Циклы часто обладают внутренней структурой, которая заметно отличается от стандартного набора, включающего соединение, оппозицию и квадратуры.
Для нас сейчас важно понять, что спираль тесна связана с циклами и что данное свойство находит свое отображение в множестве Мандельброта (рис.85). Для более подробного изучения взаимосвязи между циклом и фракталом мы обратимся к главе «Циклы и показатель Херста», а сейчас давайте рассмотрим, как выражается золотое сечение в модели Мандельброта.

Данный вопрос очень хорошо описывают два российских ученых: Щипицын Е.В. и Попков В.В. В своем труде золотое сечение в теории фракталов они показали, как связано данное явление с множеством Мандельброта. В своем курсе я хочу привести отрывок текста из их труда «Двойственность золотого сечения в теории фракталов и хаоса», который содержит в себе достаточно интересную информацию.
На рис. 86 изображено множество Мандельброта для квадратичной функции на плоскости комплексных значений параметра мнимая единица, а — соответственно действительная и мнимая части числа с). Односторонние стрелки с цифрами показывают периоды притягивающих орбит в различных областях множества Мандельброта. Двухсторонние стрелки обозначают характерные размеры множества Мандельброта, связанные с золотым сечением и числами Фибоначчи:

Здесь введены следующие обозначения:


Давайте теперь рассмотрим поведение рыночных цен в пропорциях золотого сечения. Большинство аналитиков финансового рынка в качестве инструмента для определения пропорций золотого сечения применяют шкалу фибоначи. Под последовательностью фибоначи понимают ряд чисел выстроенных в следующем порядке: 1,1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1 597, 2 584.
Основное свойство последовательности Фибоначчи - каждое число есть сумма двух предыдущих. Если обозначить n - й элемент этой последовательности Fn, то : F1 = 1; F2=1
Если взять соотношение соседних чисел Фибоначчи, то в результате получим:
F3/F2=2, F4/F3=l,5; F5/F4=5/3=l,666; F6/F5=8/5=l,6
Для всех этих отношений характерно то, что в своем пределе они стремятся к числовому значению 1.618!
На форекс мы можем применять данное значение для прогноза цен, используя числовую шкалу Фибоначчи (рис.87).

Шкала состоит из следующих уровней: 0.0; 23.6; 38.2; 50.0; 61.8; 100.0; 161.8; 261.8; 423.6. Основное предназначение данного инструмента измерить уровень отката от предыдущей волны.
Еще Чарльз Доу заметил, что типовыми являются откаты на 50%, 33% и 66%. Если тенденция сильна, то вероятная величина отката, как считал Доу, составит 33%. Обычная коррекция имеет место до величины 50%. А если коррекция составила 66% или более, то это верный сигнал о возможном переломе тенденции. Уровни, предложенные Ганном, а именно: 38%, 50%, 62%, наиболее совпадают с действительностью на финансовых рынках.
Однако мы вовсе не будем применять классические методы применения шкалы Фибоначчи. Для тех, кто интересуется данной теорией в ее стандартном понимании, советую прочитать замечательную книгу Роберта Фишера «Последовательность Фибоначчи».
Для нас, теперь числа Фибоначчи приобретут иной смысл, а правильнее было бы сказать их применение к рыночным данным будет отличаться от действующего.
Начнем с того, что помимо стандартных уровней у нас появятся еще несколько новых и не менее, а может даже, и где-то более важных в своем применении. Мы будем применять следующий список уровней: 38.2; 61.8; 76.4; 100; 161.8; 176.4; 208.0; 261.8; 276.4; 300.0 и 423.6
Несмотря на столь длинный список, мы быстро разберемся, как применяются данные уровни, и сможем реализовать их в своей торговле.
Сейчас, давайте рассмотрим, как можно представить цикл на рынке Форекс в пропорциях золотого сечения. В этом нам поможет рис.86, на котором представлено уже нам знакомое множество Мандельброта. На рис.88 представлен цикл по паре Доллар/Франк с разметкой, показывающей пропорции золотого сечения.

На рис.88 мы видим соотношения отрезков с величинами 0.618 и 0.382. Величины XI и Х2 представляют собой значения, рассматриваемые в множестве Мандельброта изображенного на рис.86. L1 и L2 были разделены на 2, т.к мы рассмотрели только одну часть цикла. Зеркальная часть цикла, представляет собой ни что иное, как имитацию, для наиболее полного сопоставления модели с множеством Мандельброта. На данном рисунке мы видим факт присутствия пропорции золотого сечения в циклах на валютном рынке.
Однако если все так просто, то почему большинство трейдеров не могут воспользоваться данными уровнями с целью успешной торговли? Ответ очень прост: они не знают, как выглядит цикл, его начальных условий, от которых и происходят все измерения. Знай мы начальные условия, т.е начало подъема, в случае если цикл восходящий или начало спуска, в случае если цикл нисходящий, мы бы с точностью смогли определить ключевые точки разворота движений внутри данного цикла.
Но все не так просто, поскольку валютный рынок представляет из себя нелинейную систему данных, в связи с чем, у него возможно несколько вариантов развития. Поэтому очень важно знать не только соотношение фибоначи к той или иной волне, но и варианты отмены данных уровней!
Также мы рассмотрим несколько вариантов применения шкалы фибоначи к различным валютным циклам.
Для того, чтобы более гибко применить золотое сечение к прогнозированию цен, мы должны воспользоваться шкалой фибоначи, которая есть в любом торговом терминале. На рис.89 показано, в каких точках происходит разворот, либо продолжение цикла.

Комментарии к рисунку:
Овалами показаны наиболее ключевые точки для разворота. Красными точками показаны важнейшие этапы развития цикла. Маленькими квадратами выделена первая волна цикла, откуда и делаются замеры. Большим прямоугольником показано ключевое развитие ситуации, которое может привести к отмене либо к продолжению цикла. Пунктирная линия, соединяющая 2 точки, показывает возможную будущую крутизну наклона развивающегося цикла, в дальнейшем мы будем называть ее переходной волной.
Уровень east - 208.0. Обычно завершает цикл. За данный уровень могут быть незначительные выходы цен. Но мы должны понимать, что когда цена вышла за данный уровень, нам нужно дождаться определенных сигналов, подтверждающих дальнейшее продолжение основного направления цикла.
Уровень south - 176.4. Завершает развитие самой длинной и импульсивной волны. В стандартной ситуации подразумевается, что данная волна заканчивается на уровне 161.8, однако, как показывает действительность, более точным является именно уровень 176.4. Но даже иногда и за его пределы выходит цена, что может сказать о скором развороте цен. Также в диапазоне между 168.1 и south характерны корректировочные движения цен.
Уровень Limited — 1.382. Поможет нам сориентироваться в случае, когда цикл идет в горизонтальном направлении (рис.90).
Уровни 100 и 76.4 являются решающими уровнями для продолжения либо отмены цикла. Как правило, все важные развороты происходят от уровня 76.4, вы можете проверить это самостоятельно на истории валютных пар, добавив этот уровень в стандартный набор фибоначи. Уровень 100 представляет собой переходной уровень к новому состоянию цикла. Его пробитие дает решающий сигнал для осуществления сделок в сторону продолжения тренда.
Уровни 50 и 38.2 для нас существенной роли не представляют, однако учитывать их все же стоит, поскольку они являются важными значениями в шкале Фибоначчи. Их пробитие, как правило, сопровождается достаточно интенсивными движениями, будь то откат от восходящей волны или восходящая (нисходящая) тенденция, пробивающая себе новые ценовые горизонты.

Комментарии к рисунку:
Красными точками показаны ключевые моменты в развитии цикла. Обратите внимание, что цикл располагается горизонтально, в отличии от обычного восходящего цикла, который идет под определенным углом (рис.91). В данном случае уровень limited, определяет максимальное значение цикла. Но как определить каким образом будет развиваться цикл: горизонтально или под углом? Ответ прост: обратите внимание на точки 1 и 2, если они располагаются относительно друг друга в горизонтальном положении, то, есть очень высокая вероятность того, что направление цикла будет горизонтальным, если точки находятся под углом, то и цикл соответственно будет развиваться достаточно интенсивно и под определенным углом.
Обратите внимание на циклы изображенные на рис.90 и рис.91 они очень похожи между собой в структуре цен, однако располагаются по-разному.

Сейчас давайте рассмотрим на рис. 92 (А, Б, В, Г, Д), как ложится шкала фибо на большинство циклов, образовавшихся в результате котирования цен на валютном рынке.



Как видно из рисунков приведенных выше, уровень 1.618 не показывает точного разворота циклов, а вот уровни south и east вполне с этим справляются.
Нужно учитывать следующие характерные моменты:
Когда цена входит в коридор между уровнями 161.8 и south, вполне возможны коррекционные движения в данном диапазоне. Уровни south и east были введены только с целью более точной ориентации на рынке, однако для тех, кто хочет действовать наверняка, уровень 161.8 остается незаменимым компасом в ориентации движения цен.
На рынке Фореке не все циклы развиваются по примерам описанным выше. Есть циклы, которые уходят за уровень east и достигают либо уровня 261.8 north(A), либо 423.6(Б) (рис.93)

Как правило, такое развитие циклов встречается очень часто на минутных масштабах. Для нас важно понять, что если уровень east будет пробит и цена не вернется в коридор south -161.8, то дальнейшее развитие цикла будет сначала до уровня 261.8 (north), а затем, после его пробития до 423.6, далее этого уровня развитие циклов не наблюдается. Если цена достигла уровня 423.6, то мы будем наблюдать нисходящее движение от данного уровня, либо плоскую коррекцию с началом нового цикла.
Для того, чтобы более точно применить шкалу фибоначи к циклам мы должны знать и понимать их развитие. В следующих разделах нашего курса мы познакомимся с структурой циклов, а также изучим их характерные особенности.
(Материалы приведены на основании: А. Алмазов. Фрактальная теория. Как поменять взгляд на рынки)

Ранее созданный нами проект "Фракталы", в переработанном варианте.
Просмотр содержимого документа
«Исследовательская работа "Фракталы и математический хаос"»
Бюджетное профессиональное образовательное учреждение Омской области
«Усть-Заостровский сельскохозяйственный техникум»
по дисциплине «Математика: алгебра и начала математического анализа; геометрия»
ФРАКТАЛЫ И МАТЕМАТИЧЕСКИЙ ХАОС
студент группы 21
Шакуров Николай Александрович
Приходько Наталья Викторовна
с. Усть-Заостровка, 2018
Глава 1. Создание фрактальной геометрии.
Как фракталы связаны с хаосом?
Глава 2. Классификация фракталов.
Области применения фракталов.
"Почему геометрию часто называют холодной и сухой?
Одна из причин заключается в ее неспособности описать форму облака, горы, дерева или берега моря. Облака - это не сферы, горы - не конусы, линии берега - это не окружности, и кора не является гладкой, и молния не распространяется по прямой.
Природа демонстрирует нам не просто более высокую степень, а совсем другой уровень сложности."
Бенуа Мандельбро
Фракталы – нечто такое, о чем я не мог написать, нечто такое, что поражает воображение многих людей, которые видят фрактальное изображение в первый раз, не зная, что это.
До недавнего времени геометрические модели природных объектов строились на основе сравнительно простых фигур: прямых, прямоугольников, окружностей, сфер, многогранников. Однако, этот набор, как не сложно заметить, трудно применим для описания сложных объектов, таких как, турбулентный поток жидкости, пористые материалы, форма облаков, кровеносно-сосудистая система, крона дерева и т.д.
Поэтому необходимы были новые геометрические понятия и методы для описания этих объектов. Одним из таких понятий и явилось понятие фрактала.
Основной идеей новой геометрии является идея самоподобия. Т.е. фрактальные структуры при различном увеличении не претерпевают в среднем значительных изменений. Например, у дерева есть ветви. На этих ветвях есть ветви поменьше и т.д. То же самое можно заметить, рассматривая горный рельеф, кровеносную систему человека и др. Сейчас очевидно, что с помощью евклидовой геометрии сложно описывать природные объекты, т.к. в ней отсутствует некоторая нерегулярность, беспорядок. В таких случаях и применяется теория фракталов. Фракталы используются при создании изображений деревьев, горных ландшафтов, облаков; при анализе сигналов сложной формы; во многих областях в физики, химии, биологии.
В отличие от евклидовой геометрии, которая рассматривает гладкие объекты, фрактальная геометрия рассматривает нерегулярные, сильно изломанные, изрезанные объекты. Для фрактальных кривых не существует понятия касательной, т.к. эти кривые в общем случае недифференцируемые.
Самоподобие является одним из определяющих свойств фрактала. Другим из таких свойств является дробная размерность. Отсюда и происхождение слова фрактал.
Когда большинству людей казалось, что геометрия в природе ограничивается такими простыми фигурами, как линия, круг, коническое сечение, многоугольник, сфера, квадратичная поверхность, а также их комбинациями. К примеру, что может быть красивее утверждения о том, что планеты в нашей солнечной системе движутся вокруг солнца по эллиптическим орбитам. Однако многие природные системы настолько сложны и нерегулярны, что использование только знакомых объектов классической геометрии для их моделирования представляется безнадежным. Как, к примеру, построить модель горного хребта или кроны дерева в терминах геометрии. Как описать то многообразие биологических конфигураций, которое мы наблюдаем в мире растений и животных. Представьте себе всю сложность системы кровообращения, состоящей из множества капилляров и сосудов и доставляющей кровь к каждой клеточке человеческого тела. Представьте, как хитроумно устроены легкие и почки, напоминающие по структуре деревья с ветвистой кроной.
Столь же сложной и нерегулярной может быть и динамика реальных природных систем. Как подступиться к моделированию каскадных водопадов или турбулентных процессов, определяющих погоду. Фракталы и математический хаос - подходящие средства для исследования поставленных вопросов.
Было принято решение провести исследование по теме «Фракталы и математический хаос». Актуальность выбранной темы была подтверждена в ходе обсуждения ее с руководителем, который одобрил выбор темы исследования. Действительно, многие даже не знакомы с понятием «фракталы» и, более того, не предполагают, что это понятие математическое. Мы понимали, что наш сборник «Галерея фракталов» будет иметь и познавательную, и эстетическую значимость для учащихся и педагогов.
Объектная область исследования – фрактальная геометрия.
Объект исследования – фракталы.
Предмет исследования – геометрические фигуры фрактального типа.
Изучив научную литературу по данному вопросу, выдвигаем
цель исследовательской работы – знакомство и изучение мира фракталов, областей их применения.
Для достижения поставленной цели необходимо решить следующие задачи:
Читайте также:


