Защита документа несовместимый хэш

Обновлено: 15.01.2025

При заключении договоров о распоряжении правами на результаты интеллектуальной деятельности большое значение имеет идентификация объектов, права на которые являются предметом договора.

Поскольку зачастую экземпляры результатов интеллектуальной деятельности (далее — РИД) весьма объёмны в цифровой форме, то классический вариант идентификации в виде, например, распечатывания, не всегда удобен: затруднительно и трудозатратно распечатывать 500 фотографических произведений в высоком качестве, ещё сложнее «распечатать» аудиовизуальное или музыкальное произведение. Про объёмные и сложные программы для ЭВМ и говорить не приходится — у комплексных проектов объём исходного кода зачастую измеряется миллионами строк кода. Например, браузер Google Chromium (на базе которого подготовлен всем известный Chrome) уже в 2015 году содержал более 15 миллионов строк кода.

С учётом таких сложностей, творческая мысль более прогрессивных участников гражданских отношений дошла до возможности приложения одноразовых финализированных компакт-дисков в качестве приложения, при этом указывались «реквизиты» компакт-диска. Однако, такой способ тоже не слишком удобен:

компакт-диски хрупки и ненадёжны;
компакт-диски ограничены в объёме;
компакт-диск имеет физическую форму, его нельзя мгновенно передать в другой город или страну;
компакт-диски теряют в популярности, и вероятно, скоро разделят судьбу 3.5"-дискет — на многих ПК считыватель таких дисков уже скорее атавизм из разряда «на всякий случай», чем реальная необходимость.

Ещё более прогрессивные участники договорных отношений стали пользоваться всеми возможностями, которые им предоставляет информационно-телекоммуникационная сеть общего пользования «Интернет» — договариваться через VoIP, заключать договоры по электронной почте, обмениваться экземплярами РИД через файлообменные сервисы.

Уже никого не удивляет ситуация, когда контрагенты и их представители друг друга вообще никогда не видели вживую.

Возникает вопрос — чем заменить традиционные «механизмы» по идентификации в соответствии с современными реалиями?

Можно указать ссылку и размер файла, содержащего экземпляр РИД, но ссылка может перестать быть активной или же имеющий возможность участник, может подменить файл по ссылке на другой с идентичным размером. Да и в случае, если речь идёт о «продаже сайта» с контентом (а не только лишь праве администрирования доменного имени), одной лишь ссылки на доменное имя будет явно недостаточно.

Как обойти эти ограничения и избежать подобных рисков?

Автор этого материала нашёл для себя ответ несколько лет назад — криптографические хэш-функции [1] .

Понятие хэш-функции

Например, рассмотрим работу хэш-функции на примере достаточно древнего по компьютерным меркам алгоритма MD5 [2] .

1.1 Создадим текстовый файл file.txt, содержащий текст ст. 1226 ГК РФ в командной оболочке bash.

1.2 Теперь получим MD5-хэш получившегося файла с помощью команды md5sum.

$ md5sum file.txt f9f3b31589779e2b5cfb41bb77cc42d5 file.txt

Вот этот набор букв и цифр «f9f3b31589779e2b5cfb41bb77cc42d5» - и есть уникальный цифровой идентификатор файла. При изменении любого символа, мы получим совершенно иной результат.

2.1 Чтобы убедиться в этом, мы проделаем аналогичные действия, но изменим положение запятой после «право следования».

2.2 А теперь посмотрим, что нам выдаст MD5:

$ md5sum file.txt a61365209311862e668c9666a50b7325 file.txt

Как видно, результат совершенно иной — его невозможно спутать с предыдущим ввиду явных отличий. То есть, малейшее изменение исходного значения - и результирующая хэш-сумма получается другой, что и является идеальным для точной идентификации. Но, как видно, длина хэш-суммы ограничена, а количество файлов - огромно, поэтому есть некоторые сложности.

3.1 Понятие коллизии

Коллизия — это случай одинакового «результата» работы хэш-функции при разных вводных данных. Несмотря на то, что получившиеся в 1.2 и 2.2 хэши очень сильно отличаются, в безграничном цифровом океане файлов невероятно много (и пока Вы читали это предложение — их стало ещё больше), поэтому коллизии неизбежны. Чем более старый алгоритм, тем менее он надёжен и криптоустойчив.

Для примера — для поиска MD5 коллизии достаточно мощности старого ПК или современного смартфона (от нескольких секунд до нескольких минут). Более современный SHA-1 в 2016 году для взлома требовал непрерывной работы на брутфорс (brute force) 12 миллионов видеокарт. Найденная в феврале 2017 года «уязвимость» от Google с названием SHAttered [3] ("shattered" с англ. - "разбитый") позволяет достичь аналогичных результатов с использованием всего лишь 110 видеокарт.

Что это значит для юристов? Это значит, что для точной и бесспорной идентификации необходимо использовать несколько разных хэш-функций.

Снимем SHA-1 с представленных Google файлов:

Как видим, хэши SHA-1 одинаковы.

Теперь посмотрим на MD5.

Так, файлы из примера Google хоть и имеют одинаковые SHA-1 хэши, но в то же время совершенно различные хэши MD5. Кроме того, в статье явно отмечается, что (пока) не существует метода добиваться одновременных коллизий для SHA-1 и MD5.

Поэтому логичный вывод: чем больше различных хэш-функций использовано — тем надёжнее идентификация. Сочетание характеристик точного размера файла, содержащего РИД и нескольких хэш-сумм позволяет однозначно и бесспорно идентифицировать конкретный файл.

При этом указанный файл также может быть и «мета-файлом» - архивом, содержащим любое количество других файлов (например, фотографические произведения или исходный код программы).

Указанный способ представляется более удобным и надёжным по сравнению с остальными:

экологичнее распечатки огромных приложений;
быстрее и надёжнее, чем запись на диск;
проще, как в реализации, так и для понимания, чем использование технологии blockchain.

С учётом того, что программ для калькуляции хэш-сумм огромное количество под любые операционные системы, а в дистрибутивах GNU/Linux они присутствуют в штатной поставке большинства дистрибутивов, единственное препятствие победоносному шествию хэш-функций по приложениям к договорам — желание или нежелание участников гражданского оборота и правоприменителей разбираться в возможностях этих алгоритмов.

Вы наверняка слышали об опасностях обмена файлами через интернет. В них тайком «подселяют» вредоносный код, который с определёнными правами может натворить на устройстве чёрт-те что. А если речь идёт об обмене важными рабочими файлами, опасность выходит на новый уровень: корпоративные данные сольют, текст договоров подменят — в общем, караул.

Для защиты на этом уровне используются криптографические алгоритмы. Базовая информация о них неплохо изложена в википедии. Если отбросить всю теорию, то обычно рассматривают симметричные, асимметричные и бесключевые криптографические алгоритмы. В первых для шифрования и дешифрования используется один и тот же ключ, во вторых — разные ключи, а в третьих ключи не используются вовсе. Каждый из типов алгоритмов применяется по-своему.

Хеш-функции

Беcключевые алгоритмы обычно используются для вычисления хеш-функций, или функций свёртки. Хеш-функция преобразовывает массив входных данных произвольной длины в выходную битовую строку установленной длины. Прелесть такого преобразования в том, что если объект изменился, то скорректируется и его хеш-функция.

Рассмотрим это на примере утилиты openssl, установленной в Linux. К примеру, у нас есть текстовый файл, содержащий «this is simple text»:

Вычислим от этого файла хеш-функцию при помощи алгоритма md5:

А теперь изменим содержимое файла:

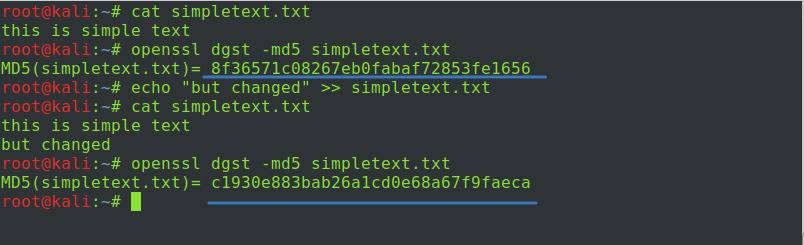
Обратите внимание: мы добавили в файл новую строку («but changed»), вычислили заново хеш от файла, и он стал другим. То есть при любом изменении содержимого файла хеш-функция не останется прежней. Это можно использовать для контроля целостности критических файлов: если их хеш изменится — системному администратору придёт оповещение. Или для проверки, загрузился ли файл полностью: если это так, на сайте опубликуется его хеш.

В Windows для вычисления хеша я рекомендую утилиту Sigcheck из пакета Sysinternals. Для примера вычислим значение хеша md5 от файла PsExec.exe:

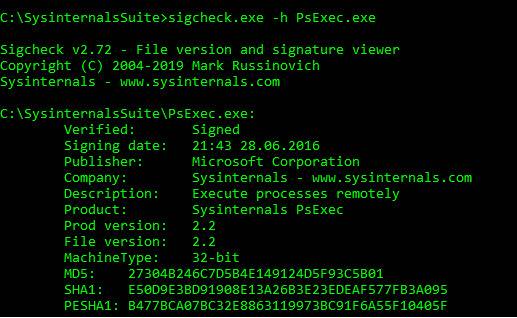
Другой вариант — использовать утилиту certutil, предустановленную в Windows. Вычислим с её помощью значение хеша md5 от файла PsExec.exe:

Также можно загрузить пакет openssl для ОС Windows. Качаем архив под нужную архитектуру процессора отсюда, распаковываем его и переходим в консоли в каталог bin. Нам нужен файл openssl.exe:

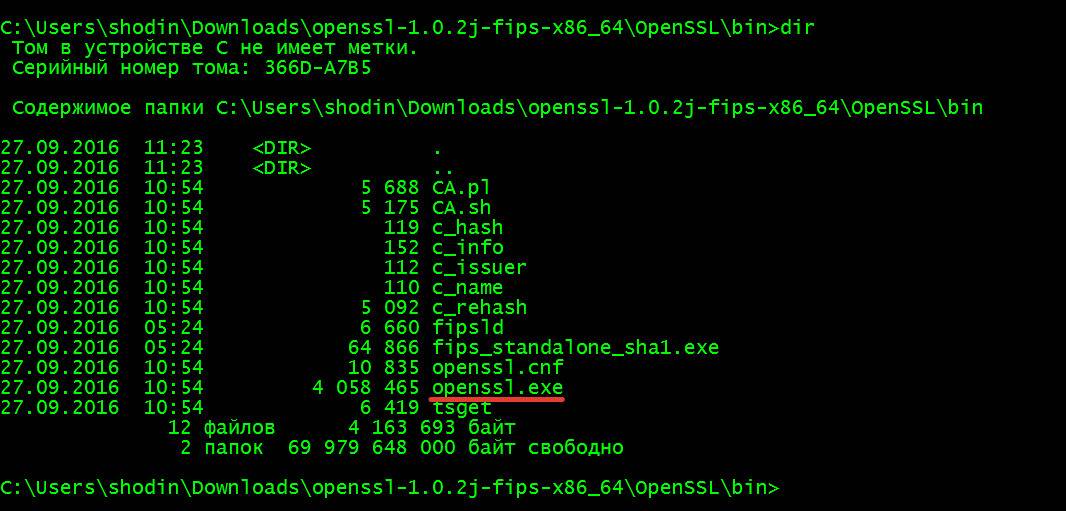
Теперь нам доступны почти все возможности пакета openssl в Windows. Например, вычислить хеш, как делали в предыдущих примерах для Linux (не забываем про абсолютные и относительные пути к файлам):

Пакет лучше переместить в каталог C:/OpenSSL, а конфигурационный файл openssl.cnf — из каталога bin в каталог OpenSSL. Избежим ошибки, как на скрине выше:

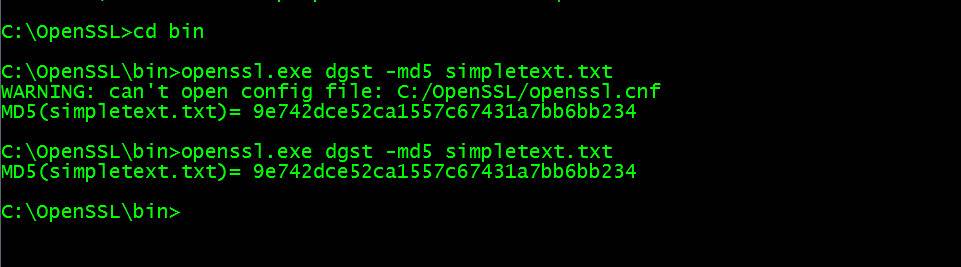
Теперь рассмотрим реализацию криптографических алгоритмов.

Симметричные криптоалгоритмы

Если говорить упрощённо, то симметричные алгоритмы шифрования применяют один ключ для шифрования и дешифрования. Таких алгоритмов много, и на практике обычно применяют те, которые имеют достаточную длину ключа и ещё не были скомпрометированы. Симметричные алгоритмы делятся на блочные (DES, RC2, Blowfish, AES, «Кузнечик» и т. д.) и потоковые (RC4, SEAL, CryptMT и другие).

Стойкость к взлому у всех блочных криптографических алгоритмов во многом определяется длиной ключа. Если она составляет 128 бит и более, шифрование считается сильным, так как для расшифровки информации без ключа потребуются годы работы на мощных компьютерах. Кому любопытно — об алгоритмах шифрования с точки зрения длины ключа можно прочитать в посте на Хабре.

Попрактикуемся: при помощи пакета openssl зашифруем созданный нами ранее текстовый файл. Для этого используем команду:

openssl enc -e -aes256 -in simpletext.txt -out simple_enc_text.txt

enc — указывает модуль для шифрования;
-e — указывает, что файлы нужно шифровать;
-aes256 — алгоритм шифрования;
-in — указывает на исходный файл;
-out — указывает на зашифрованный файл.

Выглядит это так:

Для расшифровки нужно указать введённый при шифровании ключ и используемый алгоритм. Команда примерно следующая:

openssl enc -d-aes256 -in simple_enc_text.txt -out simpletext.txt

enc — указывает модуль для шифрования;
-d — указывает, что файлы нужно расшифровать;
-aes256 — алгоритм шифрования;
-in — указывает на исходный файл;
-out — указывает на расшифрованный файл.

При шифровании симметричными алгоритмами есть несколько интересных проблем.

Длина ключа. Как уже упоминали, желательно не менее 128 бит
Сложность использования при большом количестве шифруемых объектов — приходится запоминать много параметров.
Сложность обмена параметрами шифрования (паролями, алгоритмами и подобным) — необходимо обеспечить их надёжную передачу адресату.

Такие проблемы обычно решают при помощи асимметричных алгоритмов шифрования.

Асимметричные алгоритмы шифрования

Главное преимущество асимметричного шифрования по сравнению с симметричным — возможность сторон обмениваться данными друг с другом, не используя секретные каналы связи.

Криптографическая система на основе асимметричного шифрования использует открытые (public key) и закрытые (private key) ключи для шифрования и расшифровки данных. Эти ключи образуют ключевую пару, компоненты которой связаны зависимостью, но отличаются друг от друга. Идея в том, что, зная открытый ключ, нельзя из него получить закрытый, хотя алгоритм генерации известен.

Открытый ключ передаётся по незащищённым каналам связи и известен всем. Его можно использовать для шифрования файлов и не только. Для расшифровки применяется закрытый ключ, который хранится в тайне.

У многих асимметричных алгоритмов, особенно тех, что основаны на проблемах теории чисел, минимальная длина ключа для надёжного шифрования — 1024 бит. Это сильно ограничивает их применение — симметричные алгоритмы позволяют с меньшей длиной ключа надёжно зашифровать файлы.

При практической реализации асимметричных алгоритмов обычно используют сертификат. Это файл, хранящий ключ (открытый и закрытый) в определённом формате. Подробнее об этом можно почитать в статье «Формат SSL-сертификата».

Рассмотрим два основных стандарта для реализации сертификатов шифрования.

X.509 — стандарт ITU-T для инфраструктуры открытых ключей. Определяет стандартные форматы данных и процедуры распределения открытых ключей с помощью соответствующих сертификатов с цифровыми подписями. Именно он обычно используется для электронной цифровой подписи (ЭЦП) и шифрования, например, в openssl.

OpenPGP — стандарт, выросший из программы PGP (к середине 90-х годов она распространилась в интернете как надёжное средство шифрования электронной почты). Став стандартом де-факто, PGP начал встраиваться во множество приложений и систем. С особенностями можно ознакомиться на специализированном ресурсе об OpenPGP.

Посмотрим, как это выглядит на практике. Начнём с асимметричных алгоритмов в openssl — для этого в Windows командную строку надо запустить с правами администратора.

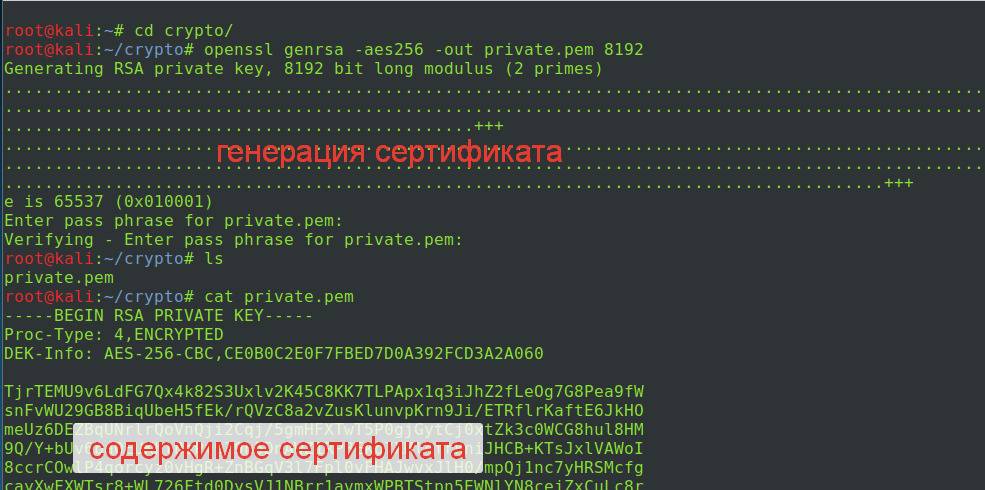
Создадим закрытый ключ в виде сертификата. Команда следующая:

openssl genrsa -aes256 -out private.pem 8912

genrsa — указывает, что мы используем модуль для генерации закрытого ключа на основе алгоритма RSA;
-aes256 — указывает на алгоритм AES для шифрования сертификата;
-out private.pem — файл для сохранения сертификата;
8912 — размер ключа.

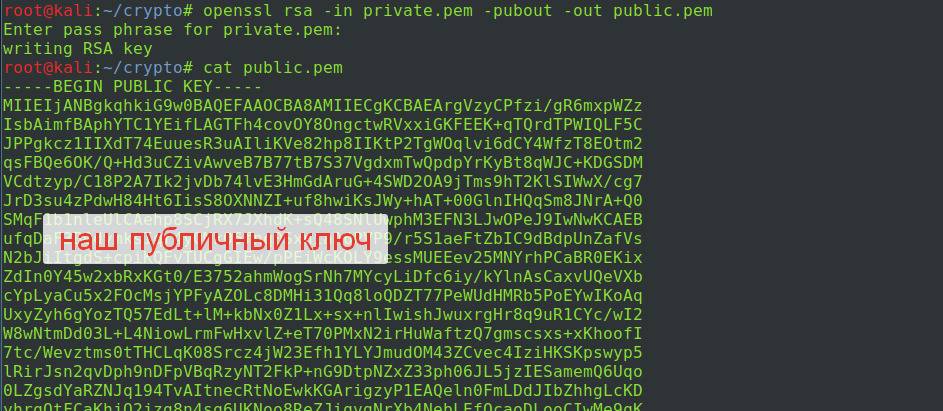
Теперь надо извлечь из полученного закрытого ключа публичный. Сделать это можно командой:

openssl rsa -in private.pem -pubout -out public.pem

rsa — модуль для работы с RSA;
-in private.pem — задаёт путь к закрытому ключу, из которого извлечём открытый;
-pubout — извлекает публичный ключ;
-out public.pem — имя файла для полученного открытого ключа.

Ключ мы получили в виде сертификата в формате pem (ASCII-файл в кодировке base64). Это не единственный формат хранения сертификатов — с другими можно ознакомиться в материале, который уже рекомендовался выше.

Стоит учесть, что таким сертификатом мы не сможем зашифровать объект, превосходящий по размеру сам сертификат. Поэтому поступим хитрее: зашифруем файл симметричным алгоритмом, а ключ шифрования от этого алгоритма зашифруем при помощи сертификата. По шагам:

Генерируем сертификаты (пару из открытого и закрытого ключа).
Шифруем текст симметричным алгоритмом AES (его вроде бы ещё не взломали). Предположим, получим файл enc.1.
Далее выбранный для шифрования пароль шифруем публичным ключом (предположим, получим файл enc.2).
Теперь можно передать зашифрованный файл enc.1 и файл enc.2 по незащищённому каналу связи.
На другом конце у получателя должна быть вторая часть ключа (закрытый ключ). Ей он вначале расшифровывает файл enc.2 и извлекает оттуда пароль для дешифровки файла enc.1.
…
Profit!

Вот как это выглядит на практике. Вначале шифруем текстовый файл алгоритмом AES (пароль 123456):

Теперь сохраним наш пароль (123456) в файл pass.txt. И зашифруем файл при помощи сертификата. Команда:

openssl rsautl -encrypt -inkey public.pem -pubin -in pass.txt -out pass.ssl

rsautl — включаем модуль для шифрования, дешифрования и подписывания данных алгоритмом RSA;
-inkey public.pem — указывает путь к открытому ключу;
-pubin — указывает, что файл ключа является публичным ключом;
-in pass.txt — файл для шифрования;
-out pass.ssl — выходной зашифрованный файл.

Теперь можем переслать этот файл по открытому каналу связи. Перехват такой информации мало что даст злоумышленнику, если у него нет закрытого ключа. Попробуем расшифровать файл закрытым ключом и извлечь пароль для расшифровки:

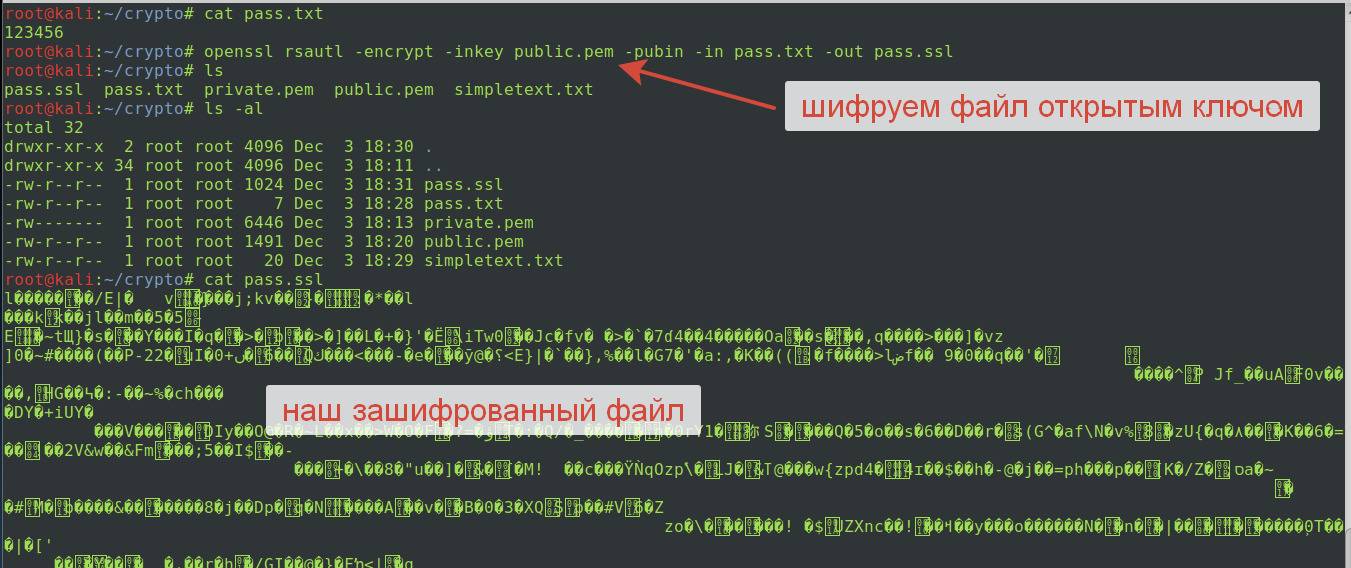
Мы получили пароль — теперь с его помощью можно расшифровать файл, который мы с ним зашифровали при помощи алгоритма AES:

В этой статье я показал, как работать с шифрованием файлов. В следующей мы подробнее остановимся на стандарте OpenPGP и научимся использовать шифрование в электронной почте.

Работа с криптографическими алгоритмами — это лишь малая часть одного из курсов факультета информационной безопасности Geek University. Ближайший поток стартует 28 декабря — неплохой подарок на Новый год ;) Кроме того, до 29 декабря вы сможете выбрать ещё один факультет Geek University для себя или в подарок и получить его бесплатно.

Хэш-функции применяются для тестирования логических устройств, для быстрого поиска и проверки целостности записей в базах данных.

В криптографии хэш-функции применяются для решения следующих задач:

построения систем контроля целостности данных при их передаче или хранении,
аутентификация источника данных.

$\begin H_0=v, \\ \\ H_i= f(M_i, H_), i=1,\dots,N, \\ \\ h(M)=H_N. \\ \end$

При таком подходе свойства хеш-функции полностью определяются свойствами одношаговой сжимающей функции .

9.2 Электронная подпись

9.2.1 Общие положения

Появление криптографии с открытым ключом позволило решать задачи, которые ранее считались неразрешимыми. К таким задачам относится использование цифрового аналога собственноручной подписи абонента - электронной цифровой подписи (ЭЦП).

Задачи, которые решает подпись:

Для реализации схемы ЭЦП необходимы два алгоритма: алгоритм генерации подписи и алгоритм проверки. Надежность схемы ЭЦП определяется сложностью следующих задач:

Заметим, что между ЭЦП и собственноручной подписью имеются различия, хотя они и служат для решения одинаковых задач. Так, ЭЦП зависит от подписываемого текста, различна для разных тестов. Кроме того, ЭЦП требует дополнительных механизмов, реализующих алгоритмы ее вычисления и проверки. Наконец, принципиальной сложностью, возникающей при использовании ЭЦП, является необходимость создания инфраструктуры открытых ключей. Эта инфраструктура состоит из центров сертификации открытых ключей и обеспечивает возможность своевременного подтверждения достоверности открытой информации, необходимой для проверки ЭЦП, что необходимо для предотвращения подделки подписи.

Некоторые наиболее употребительные схемы ЭЦП

В настоящее время имеется большое количество различных схем ЭЦП, обеспечивающих тот или иной уровень стойкости. Существующие схемы можно классифицировать таким образом:

Схемы на основе систем шифрования с открытыми ключами,
Схемы со специально разработанными алгоритмами вычисления и проверки подписи,
Схемы на основе симметричных систем шифрования. Рассмотрим некоторые схемы.

9.2.2 Схема Эль-Гамаля

Безопасность схемы основана на трудности вычисления дискретных логарифмов в конечном поле. Для генерации пары ключей выбирается простое число и два случайных числа, и , оба меньше . Затем вычисляется

$r=g^<k> (\mod p) \qquad \text\qquad s = (M-xr)\cdot k^ (\mod (p-1)).$

Для проверки подписи нужно убедиться, что

$<y> ^ \cdot ^ Схема Эль-Гамаля послужила образцом для построения большого семейства во многом сходных по своим свойствам схем подписи. Пример 9.1 Выберем и , а секретный ключ . <img class=$
- число, обратное по модулю , " />
существует, так как и - взаимно просты.

Используемые на практике алгоритмы хеширования достаточно сложны, поэтому будем использовать учебные алгоритмы формирования хеш-значения . Схему учебных алгоритмов хэширования предложила Васильева И.Н. [1].

Первый учебный алгоритм хеширования

$p=79,\qquad g=15,\qquad x=34,\qquad k=17.$

$\begin<equation*> \begin h_1=(h_0+n_1)^2 (\mod 79) =36, \\ h_2=(h_1+n_2)^2 (\mod 79) =31, \\ h_3=(h_2+n_3)^2 (\mod 79) =26 \\ h_4 = (h_3+n_4)^2 (\mod p)$
. Для рассматриваемого примера получили:

- отрицательное, следует взять его по модулю .

$s=23 \cdot 5 (\mod 79-1)=37.$

Для проверки правильности вычисления полученной цифровой подписи следует произвести ее проверку с помощью открытого ключа абонента и убедиться, что подпись подлинная.

(\mod p)" />
, а затем их произведение по модулю .

$\begin<equation*> \begin y^ (\mod p)= 38\cdot 27 <img class=$

(\mod p)" />
, значение было получено ранее.

$g^ В примере (\mod p)$
, если равенство выполняется - подпись подлинная, то есть она была вычислена правильно.

В примере получили , равенство выполняется, значит, подпись сгенерирована правильно.

Второй учебный алгоритм хеширования

Начальное значение принимается равным числу десятичных разрядов в .

$h_i =(M_i+ 2\cdot h_<i-1> +1)^ (\mod p-1),\ i=1,\dots,n.$

(\mod p)" />
, а затем их произведение по модулю :

$\begin<equation*> \begin y^ (\mod p)= 35\cdot 15 (\mod 58) = 24;\\ h_2 = (5 + 2\cdot 24 + 1)^2 (\mod 58) = 16;\\ h_3 = (6 + 2\cdot 16 + 1)^2 (\mod 58) = 13;\\ h_4 = (9 + 2\cdot 13 + 1)^2 (\mod 58) = 20;\\ h = h_4 + 1 = 21; \end$

$g^ В примере (\mod p)$
, если равенство выполняется - подпись подлинная, в противном случае - фальшивая.

$53\neq 6$

В нашем примере . Равенство не выполняется, значит, подпись фальшивая.

Одно из полезных применений асимметричного шифрования — работа с электронной подписью. Рассказываем, как устроена ЭП изнутри и где она применяется.

Что такое электронная подпись

Электронная подпись — это технология, которая помогает подтвердить подлинность электронного документа: договора, справки, выписки или чего-то ещё.

Если упрощённо, работает так:

👉 Есть некий документ, подписанный ЭП

👉 С помощью специальной программы можно проверить подлинность этой подписи и документа

✅ Если программа говорит, что всё окей, то мы можем быть уверены: документ подписал именно тот, кто в нём указан; и с момента подписания в документе ничего не изменилось.

❌ Или программа может сказать, что подпись не совпала. Это значит, что либо документ подписал другой человек, либо после подписания кто-то изменил этот документ (например, дописал ноль в стоимость контракта). Так мы поймём, что этому документу нельзя доверять.

С технической точки зрения ЭП — небольшой файлик, который прилагается к искомому документу. Файлик пересылается вместе с основным документом, его можно передавать по открытым каналам связи, в нём нет ничего секретного.

Электронная подпись нужна, чтобы защищать договоры, выдавать официальные справки, заключать сделки и участвовать в торгах по госзакупкам.

Основа ЭП — асимметричное шифрование

Как работает: сертификаты

Электронная подпись состоит из двух принципиальных частей:

Сертификат для удостоверения подписывающего.
Криптографическая часть для проверки подлинности документа.

Грубо говоря, ЭП должна гарантировать, что документ подписали именно вы и что вы подписали именно этот документ.

В сертификате хранятся данные о владельце подписи:

кто владелец этой подписи;
открытый ключ для проверки подписи;
когда заканчивается срок действия подписи;
какого уровня документы можно подписывать этой подписью;
кто выдал сертификат;
и другие служебные данные.

Но смысл сертификата не в том, что там хранятся эти данные, а в том, кто эти данные туда положил. В России сертификаты и ЭП выдают специальные удостоверяющие центры — это компании, которые гарантируют, что сертификат выдаётся именно тому, кто в этом сертификате указан.

Чтобы получить сертификат, вы приходите лично в эту компанию (удостоверяющий центр), показываете документы, фотографируетесь. Вас заносят в базу удостоверяющего центра и выдают ключи электронной подписи. Так все участники электронного документооборота будут уверены, что все документы, подписанные вашими ключами, подписаны именно вами.

Как работает: алгоритмы шифрования

Допустим, вы уже сходили в удостоверяющий центр и получили на флешке сертификат и ключ электронной подписи. Теперь нужно скачать специальный софт, который и будет подписывать ваши документы и проверять чужие на подлинность.

Проблема в том, что ЭП основана на алгоритмах асимметричного шифрования, а их много: разложение на простые множители, дискретное логарифмирование, эллиптические кривые и множество других. Ключ из одного алгоритма не подойдёт для использования в другом, поэтому в России договорились использовать стандарт шифрования ГОСТ Р 34.10-2012, основанный на эллиптических кривых. Все государственные органы работают только с таким алгоритмом и не принимают другие ЭП.

Это значит, что нам нужен специальный софт, в котором уже есть этот алгоритм. Чаще всего используют КриптоПРО, реже — ViPNet CSP. С помощью этих программ можно подписать документы и проверить сертификаты на подлинность.

Принцип работы электронной подписи

Электронная подпись — это асимметричное шифрование наоборот: вы зашифровываете закрытым ключом, а расшифровать может кто угодно с помощью открытого ключа, который доступен всем.

Разберём по шагам:

В удостоверяющем центре вы получаете сертификат и ключ электронной подписи. Это закрытый ключ, который передавать никому нельзя. Открытый же ключ хранится в самом сертификате, который прикладывается к каждому документу и доступен всем.
Берёте нужный документ и получаете его криптографический хеш. Хеш — это небольшая строка, которая представляет собой «цифровой отпечаток» файла. У каждого файла с уникальным набором битов будет уникальный хеш, причём он всегда одинаковой длины. Подробнее о хешах мы писали, когда разбирали скандал с паролями Фейсбука.
Шифруете этот хеш своим закрытым ключом. Полученный результат шифрования добавляете к исходному документу.
Туда же добавляете сертификат, чтобы все могли проверить и убедиться, что документ подписали вы.

А что если подменят сам сертификат?

Все сертификаты, которые выдаёт удостоверяющий центр, тоже подписываются электронной подписью. Чтобы проверить подлинность сертификата, можно зайти на официальный сайт удостоверяющего центра и скачать открытый ключ для проверки. Если хеш самого сертификата совпадает с хешем, который мы получили с помощью открытого ключа с сайта — значит, и сам сертификат подлинный.

Читайте также: