Трафарет синусоиды как сделать
Подскажите, как нарисовать правильную синусоиду в AutoCAD'е 2002.
Подозреваю, что без Lisp'a или VBA не обойтись. Но ни на том, ни на другом для AutoCAD'a ничего не писал. Если кто-нибудь поделиться примерчиком - думаю разберусь (программировать время от времени приходится, правда не на лиспе и не на бэйсике).
По точкам, как в школе, все просто. Рисуешь окружность, делишь на N частей, развертываешь окружность ну и т.д.
__________________
. Не пытайся гнуть ты ложку,
Не вяжи её узлом.
Ложка - ложка понарошку,
А по правде, - это лом!
Артиллерист - вертолётчик. Дипломированный инженер-механик. Technologist
Подскажите, как нарисовать правильную синусоиду в AutoCAD'е 2002.
Подозреваю, что без Lisp'a или VBA не обойтись. Но ни на том, ни на другом для AutoCAD'a ничего не писал. Если кто-нибудь поделиться примерчиком - думаю разберусь (программировать время от времени приходится, правда не на лиспе и не на бэйсике).
--
Спасибо.
Я рисовал пружину в MDT2002 (сжатия или растяжения неважно, главное нужные шаги и диаметр проволоки брать минимальный), взрывал её, чтобы автокад видел как обычный 3D-Солид и всталял в автокад. Потом делал проекцию на плоскость.
Можно сказать идеальная синусоида получалась
Хотя возможно существуют и менее замороченные способы. Но такой меня устраивал.
__________________
Мы можем делать быстро, качественно и недорого, выбирайте любые 2 условия.:search:
Инженерным калькулятором находите значения sin(0-90) можно через 10 градусов. Отмечаете точки на координатной оси (по ординате -1, 0, +1; по абсцисе 0-360 град). Сначала отмечаете 9 точек до 90 градусов, объединяете сплайном, а дальше зеркалите. Как по старинке
__________________
-Сэр, мы окружены.
-Это великолепно. Теперь мы можем атаковать в любом направлении.
не путайте (+ 0.1 x) возращает х+0.1, а х=х+0.1 это (setq x (+ 0.1 x))
Короче все по порядку
(setq x 0 tmp nil); присваивает х=0, tmp=nil (на случай повторного запуска)
(command "_zoom" "_o"; масштабирование экрана по объекту
(entmakex (append ; создать объект из суммы списков
(list (cons 0 "LWPOLYLINE")(cons 100 "AcDbEntity")(cons 100 "AcDbPolyline") (cons 90 100) (cons 70 0)); разомкнутая полилиния со 100 вершинами
(mapcar ;преобразовать список с помощью
'(lambda (x); анонимная функция с аргументом х
(list 10 x (sin x))); вернет список: 10 - dxf код вершины, x, sin(x)
(repeat 100 (setq tmp (cons (setq x (+ 0.1 x)) tmp))))))""); список из 100 чисел от х с приращением в 0.1 (в обратном порядке)
Zenon, за аттачмент спасибо, но Ваш [FONT=Courier New]sinus.dwg[/FONT] не открывается. Может еще раз или в другое место можно выложить?
------------------------------------------------------------------------------------------------------
_Дима, а на экран то как все посчитанное вывести?
а он вообщето и выводит, даже зумирует во весь экран - скопируй код, вставь в командную строку и enter.
ГИП, технолог по холодильному проектированию
например:
в Excel составил таблицу "x" - "sin(x)"
в Мастере диаграмм получил график
нажал PrintScreen
открыл Autocad
вставил
подогнал по высоте и ширине
и срисовал поточечно
Короче все по порядку
(setq x 0 tmp nil); присваивает х=0, tmp=nil (на случай повторного запуска)
(command "_zoom" "_o"; масштабирование экрана по объекту
(entmakex (append ; создать объект из суммы списков
(list (cons 0 "LWPOLYLINE")(cons 100 "AcDbEntity")(cons 100 "AcDbPolyline") (cons 90 100) (cons 70 0)); разомкнутая полилиния со 100 вершинами
(mapcar ;преобразовать список с помощью
'(lambda (x); анонимная функция с аргументом х
(list 10 x (sin x))); вернет список: 10 - dxf код вершины, x, sin(x)
(repeat 100 (setq tmp (cons (setq x (+ 0.1 x)) tmp))))))""); список из 100 чисел от х с приращением в 0.1 (в обратном порядке)
как построить такую же синусойду только по формуле?
y = (a0/ 4) [1 + sin( Pi x / s - Pi /2)]
a0= 550 mm
s = 190 mm
как построить такую же синусойду только по формуле?
y = (a0/ 4) [1 + sin( Pi x / s - Pi /2)]
a0= 550 mm
s = 190 mm
Люди, умеющие рисовать :), подскажите как в фотошопе или гимпе технически грамотно волну нарисовать (синусоиду) ровную :) ?
PS и Gimp немного для других целей.
Если очень хочется извратом пострадать, то Python Script к вашим услугам.
из полуокружностей составить?

> из полуокружностей составить?
И в каком месте это будет синусоида?
Угу. в итоге так и сделал. Сосавил впритык окружности одинакового диаметра, и посрезал верх/низ через один

евгения слушай - никакая это не синусоида, если тебе конечно нужна достоверная синусоида
Волна нужна была.

3 команды в гнуплоте заменят вам пол часа мастурбации в фотошопе/гимпе.

Давно хотел узнать, а можно ли как-нибудь в гимпе использовать автофигуры, как в сами_знаете_где?

> Давно хотел узнать, а можно ли как-нибудь в гимпе использовать автофигуры, как в сами_знаете_где?
Данный онлайн конвертер предназначен для перевода любой фотографии в двухцветный трафарет.
Для этого просто загрузите любое изображение, выберите нужные цвета и сохраните полученный результат.
Смотрите также:

Генератор оттенков

Генератор оттенков заданного цвета в форматах HEX, RGB и HSL

Конвертер изображений в base64

Кодирование любых изображений в 64-разрядный код base64

Конструктор Clip-Path

Конструктор для создания фигур с помощью CSS-свойства Clip-Path
Сделать заказ или получить консультацию:
Контакты:
В 1634 году математик Роберваль рассмотрел синусоиду в качестве вспомогательной кривой, которая образовалась проекциями точки окружности. Учёный доказал, что тригонометрическая функция пересекает прямую во множественных точках. Для её построения используются прямоугольные координаты. График уравнения имеет следующий вид: y=a+b cos (cx+d).
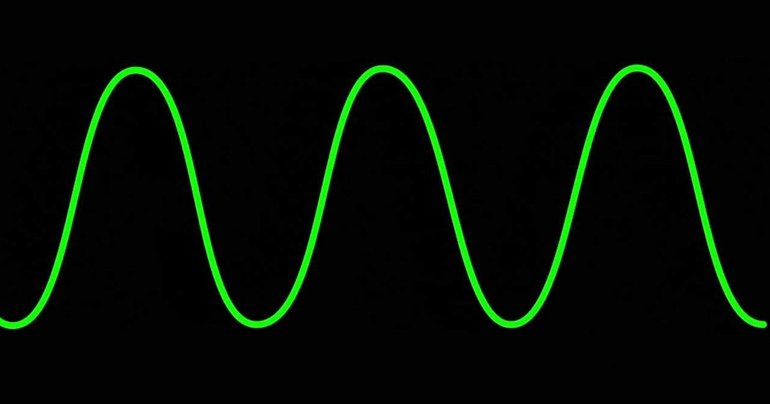
Основные понятия
Кривая получается из синусоидальной дуги путём смещения к пи/2 в сторону со знаком минус. Кривая представляет график функции у=sin x. В формуле синусоиды y=a+b cos (cx+d) присутствуют следующие аргументы:
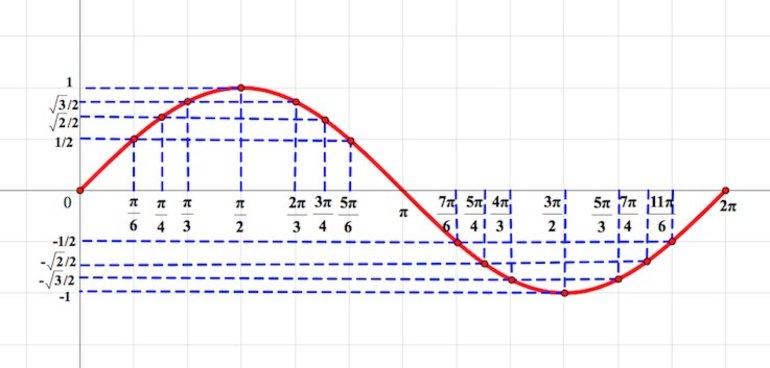
- a: показывает сдвиг графика синусоиды по оси Oy (чем больше значение, тем выше прямая);
- b: описывает растяжения функции по оси Oy (чем выше постоянная, тем сильнее колебания);
- c: определяет растяжение по оси Ох (если постоянная увеличивается, наступает период колебаний);
- d: описывает сдвиг по оси Ох (если d увеличивается, тогда при построении синусоиды учитывается сдвиг в область со знаком минус по оси абсцисс).
Сжатие, растяжение либо сдвиг кривой приводит к изменению величины. Явления называются гармоническими колебаниями. Примеры синусоиды: экспонент или показательная функция в виде винтовой линии, проведённой на плоскости, скрученный провод, развёрнутый рулон бумаги.
Особенности построения
Чтобы выявить свойства синусоиды, необходимо построить её график, провести исследование синуса. В алгебре под функцией представлена плоская кривая, которая выражает закон колебания sin с учётом изменения центрального угла. Сама синусоида строится в схематической последовательности:
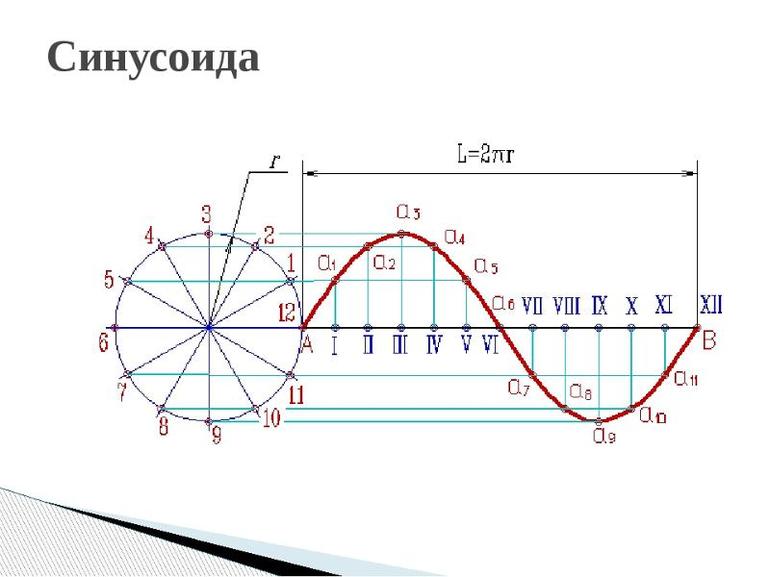
- проводится горизонтальная ось, на которой откладывается заданная длина волны;
- отрезок делится на равные части;
- слева чертится окружность с радиусом, равным величине амплитуды;
- окружность делится на 12 одинаковых частей;
- через полученные точки проводятся прямые;
- из точек проводятся перпендикуляры к оси.
График можно построить на онлайн ресурсе либо с помощью специальных программ (Excel). Для расчёта используется калькулятор, основная формула y=sin х. При решении задач учитывается длина волны, которая равна 2 пи. Такое преобразование объясняется тем, что значение функции при любом икс совпадает с её периодичностью x+2π.
Пересечение оси Ох происходит в точках перегиба πK. Максимум достигается при положительном π/2+2πK, а обратное — -π/2+2πK. Свойства кривой проявляются в частном либо комплексном виде:
- размах;
- растяжение/сжатие;
- фазовые колебания;
- круговая частота.
При сдвиге графика влево к значению пи/2 образуется косинусоида. Любое изменение величины характерно для квадрата с гармоническими колебаниями. Примеры подобных явлений: движение маятника, сбои с напряжением в электросети. Другой случай с синусоидальными колебаниями — звук. Он редко бывает чистым, соответствуя y=A sin wt, где:
- А (а) — модуль неизвестной (расстояние от начала координат до точки А);
- w — угловая частота;
- t — время.
Чаще издаются обертоны, для которых характерны низкие амплитуды. Подобные явления изучаются в школе на уроках физики в старших классах.
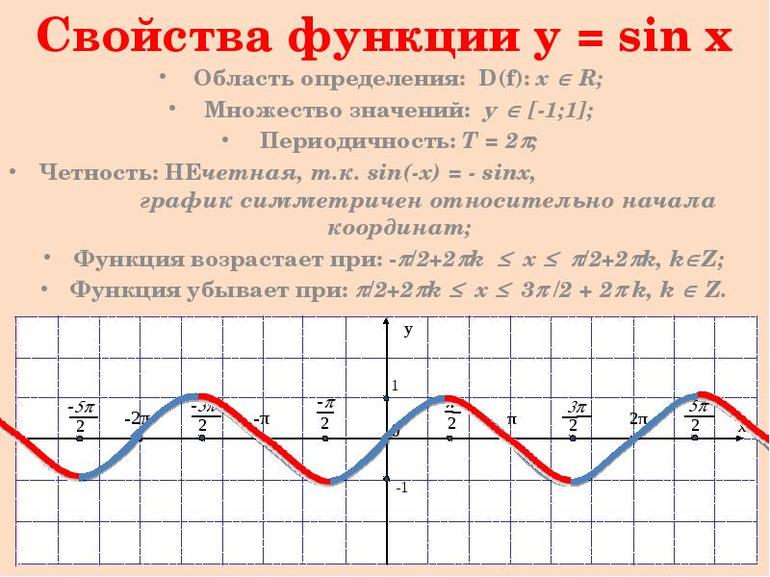
Свойства и доказательства
К главным свойствам синусоиды относятся область значений (включая нуль) и определений, чётность/нечётность, периодичность, точки пересечения с осью координат, промежуточности постоянства, убывания и возрастания, минимум и максимум. При пересечении графика функции (ГФ) с осью Ох результат равняется нулю. Под значением синуса подразумевается ордината соответствующей точки единичной окружности.
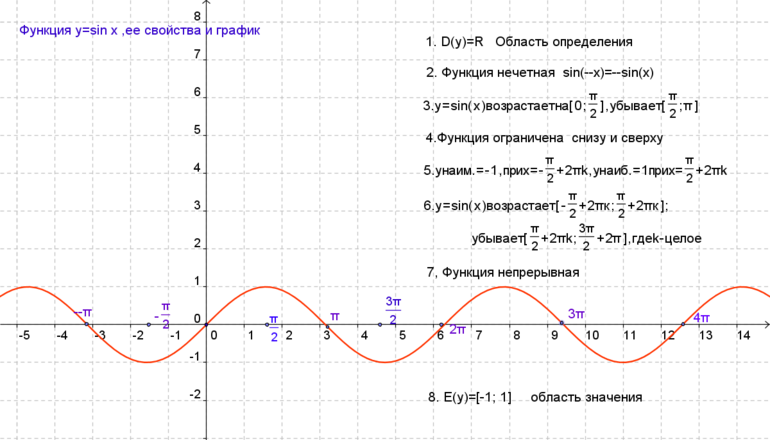
Так как через круг в одной области можно провести только одну прямую, перпендикулярную оси, поэтому для области определения функции подходят все числа. Такое свойство записывается следующим образом: D (sin x) = R.
Значения ординаты единичной окружности (ЕД) расположены на отрезке [—1; 1]. Они принимают значения от -1 до 1. Через любую точку указанного промежутка оси ординат, равного диаметром ЕД, проводится прямая, перпендикулярная оси ординат. Таким способом получается точка с рассматриваемой ординатой.
Из свойства вытекает следующее: функция y= sin x имеет область значений (-1; 1). Утверждение записывается так: E (sin x)=(-1; 1). Максимальное значение функции равняется единице. Подобное возможно, если соответствующей точкой ЕД является точка А. Минимальное число y равно -1 в случае, когда точкой ЕД является В (х=пи/2 +2пиk, где k принадлежит области Z.
Нечётность и постоянство
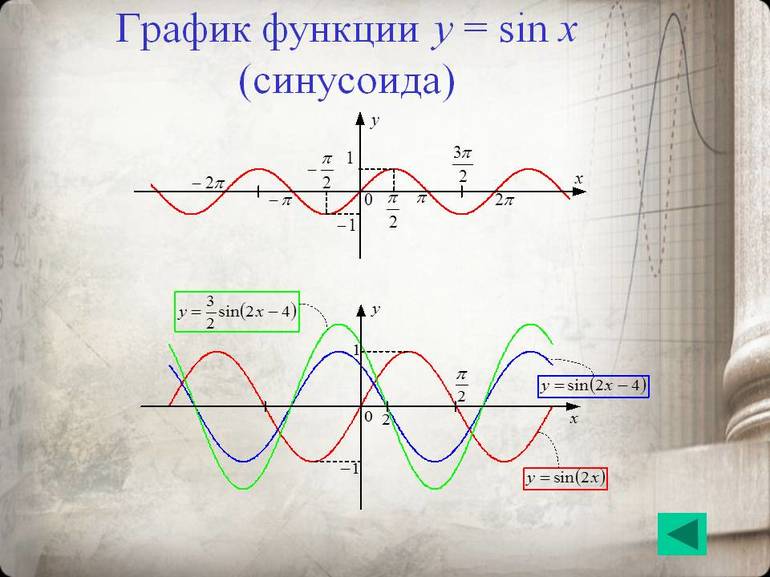
Функция считается нечётной, если sin (-x)=- sin x. Её график симметричен по отношению к началу координат. Сам синус является периодической величиной, у которой наименьший положительный период. Через отрезок 2пи вид кривой повторяется. Это свойство учитывается при построении графика.
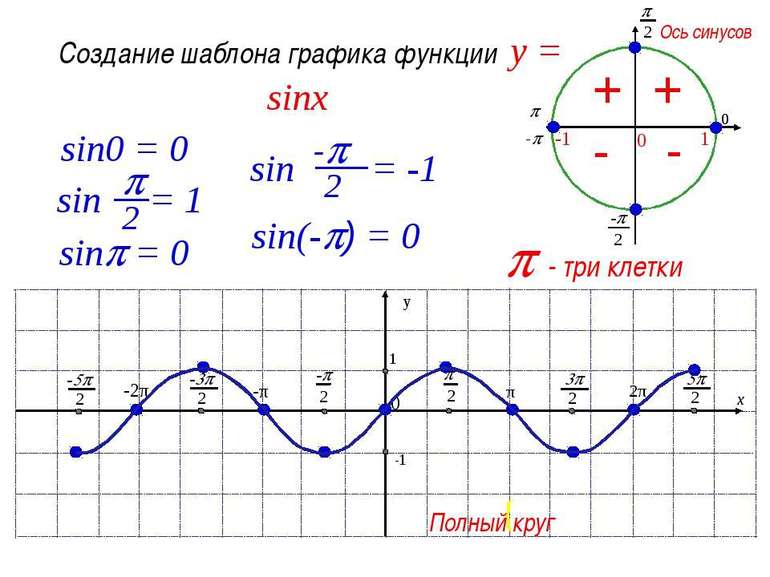
Предварительно чертится кривая на любом отрезке соответствующей длины. При переносе линии влево и вправо соблюдается шаг в kT=2 πk, где k — любая натуральная цифра. Для вычисления точек пересечения линии с осями координат используется равенство х=0. Если значение подставить в функцию, получится следующее: y=sin 0=0. В таком случае график проходит через начало координат.
Так как y равен нулю, поэтому можно рассчитать х, воспользовавшись формулой y= sin x. Координата подходящей точки ЕД равняется нулю. Такое явление будет наблюдаться только в случае, если на ЕД будут выбраны точки D либо C, при x=πk, k принадлежит Z.
Функция имеет положительное значение в первой и во второй четвертях. На этих промежутках sin x больше нуля, а любое значение х находится в пределах 0-π. При решении задач учитывается период при всех x, принадлежащих отрезку (2πk; π+2πk), где k принадлежит Z. Функция считается отрицательной в третьем и четвёртом квадрате. При этом sin меньше нуля, а иск находится в пределах (пи+2пиk; 2пи+2пиk), k принадлежит области Z.
Больше и меньше
С учётом периодичности y с периодом T=2π исследуется функция на возрастание и убывание на любом отрезке длиной в 2пи. Если T= (-π/2;3π/2), а х принадлежит данному промежутку, тогда при увеличении аргумента изменится в большую сторону и ордината. Следовательно, на указанном отрезке синусоида возрастает.
Если учитывать её периодичность, можно прийти к выводу, что она возрастает на каждом интервале (-π/2+2πk; π/2+2πk), k принадлежит Z. Если х находится на отрезке (-π/2;3π/2), тогда при увеличении аргумента ордината ЕД уменьшается, а функция убывает. С учётом периодичности синусоиды можно сделать вывод, что она бывает на каждом отрезке (π/2+2πk;3π/2+2πk), k находится в области Z.
Основываясь на проведённом исследовании, строится график y=sin x. С учётом периодичности 2π предварительно строится график на любом отрезке соответствующей длины. Чтобы точно построить точки, рекомендуется придерживаться значения синуса (ордината ЕД). На основе нечётности проводится кривая, симметричная началу координат. При этом необходимо придерживаться интервала (-π;0). Так как линия строится на отрезке длиной 2π, поэтому учитывается периодичность величины.
Вид графика повторяется на каждом отрезке с аналогичной длиной. Таким способом получается синусоида. Рассматриваемая тригонометрическая функция получила широкое применение в технике, физике и математике. Большинство процессов, включая колебания струн, напряжения в цепи, описываются с помощью функции, задаваемой формулой y= A sin (wx + f). Подобные явления считаются гармоническими колебаниями.
Кривая получается из синусоиды за счёт разных колебаний и путём параллельного переноса вдоль оси Ох. Чаще изменения результата связаны с функцией времени t. В таком случае используется формула y= A sin (wx + f), где через А обозначается амплитуда колебания, через w — частота, f — начальная фаза, 2пи/f — период колебания.
Когда речь заходит о комплексных числах, в первую очередь вспоминают о преобразовании Фурье и прочих аспектах цифровой обработки сигналов. Однако у них есть и более наглядная интерпретация, геометрическая — как точки на плоскости, координатам которой соответствуют действительная и мнимая часть комплексного числа. Рассматривая некоторую кривую как совокупность таких точек, можно описать её как комплексную функцию действительной переменной.

▍ Окружность
Когда нам нужно начертить окружность в реальной жизни — мы берём циркуль и, уперев его одним (острым) концом, а другим (с грифелем) постепенно вращая, оставляем след на бумаге. В математике это делается аналогично — в роли циркуля выступает мнимая единица , а в роли вращения — возведение её в степень переменной , которую можно интерпретировать как момент времени (а в данном конкретном случае — как угол поворота). Здесь вектор описывает полный круг при изменении значения от до — что также удобно интерпретировать как четверти на координатной плоскости, когда при изменении целой части одна из проекций на координатную ось меняет свой знак.
Возможно, выражение кому-то может показаться несколько непривычным, поскольку оно не употребляется в традиционных учебниках математики. В таком случае можно использовать каноническую запись, перейдя к основанию : .
Также в качестве основания можно использовать минус единицу: , что часто используется в Wolfram Mathematica для описания единичных комплексных констант.
Разница между функциями , и состоит лишь в периоде для полного оборота вектора по окружности — , или ; а единицами измерения углов соответственно будут радианы, пол-обороты и кварт-обороты (квадранты). Запись с экспонентой является исторически первой, однако её сложно назвать наглядной — возведение в комплексную степень несколько контринтуитивно. В этой же статье вариант выбран по причине его большей компактности и наглядности.
▍ Эллипс
Эллипс можно начертить растягиванием окружности вдоль одной из осей. Но в таком случае это получится самый обычный параметрический график с участием тригонометрических функций, но без участия комплексных чисел. В комплексных же числах эллипс можно представить как сумму двух векторов разной длины и вращающихся с одной частотой, но в противоположные стороны:
Поскольку в комплексных числах результат суммы тоже не зависит от порядка слагаемых, эту же анимацию можно представить чуть по-другому:
Используя формулу в полярных координатах, можно начертить эллипс одним вектором, но с динамически изменяемой длиной:
Несмотря на то, что фигуры получаются одинаковыми, положение точки (и скорость) в каждый момент времени не совпадают, что хорошо видно на анимации. Поэтому производные этих эллипсов совпадать не будут:

Примечательно, что производная от эллипса, задаваемого суммой двух векторов, осталась тем же эллипсом с теми же пропорциями. Ну а теперь — самое главное преимущество комплексных чисел: чтобы повернуть эллипс на произвольный угол, достаточно просто умножить его на единичный вектор с необходимым углом поворота (phi):
▍ Гипотрохоида и прочее
Усложнение получаемых фигур достигается усложнением их мат.модели. Достаточно изменить частоту второго вектора, и можно получить нечто более интересное, а именно — математическую модель спирографа:
Здесь необходимо обратить внимание на то, что для получения замкнутой кривой одного оборота по окружности оказалось недостаточно — их потребовалось уже 3 и 4 соответственно. Это явилось следствием того, что период второго вектора не укладывается нацело в период первого вектора.
Можно и дальше добавлять векторы и получать всё более и более сложные фигуры:
▍ Синусы и синусоидные ленты
Давайте немного отвлечёмся от окружностей и начертим синус. Традиционная запись синусоиды выглядит так:
В комплекcном виде формула для синусоды выглядит ненамного сложнее
а график, естественно, выглядит аналогично:

Легко видеть, как была получена это формула — правую часть равенства мы умножили на мнимую единицу, знак равенства заменили на плюс, а и заменили на одну и ту же параметрическую переменную — . Принципиальная разница между этими формулами получилась в том, что теперь можно взять и повернуть синусоиду, просто умножив её на единичный вектор с нужным углом наклона (здесь 45°). Подобные трансформации синусодиды могут потребоваться для того, чтобы направлять её вдоль заданных кривых:

В параметрической форме записи можно модулировать координаты, получая таким образом различные деформации синусоиды, на первый взгляд не имеющих ничего общего с оригиналом:




Количество синусоид можно увеличивать, добиваясь эффекта заполнения пространства за счёт равномерного сдвига фаз между ними:

Здесь — количество синусоид, а — порядковый номер синусоиды.
Смещение можно задавать и просто смещением координат — как по одной координате, так и по двум:


▍ Розетты
Теперь можно попробовать и более сложные варианты — добавить фигурам заполнения. Есть два пути для этого:
1) взять центральную кривую, от которой в обе стороны осциллирует синусоида. Это творческий метод, поскольку внутренняя и внешняя огибающие будут зависеть от множества параметров и могут оказаться весьма неожиданными. Здесь также дополнительной сложностью будет вычисление нормали для синусоидной ленты. Несмотря на то, что её легко вычислить дифференцированием нашей кривой (и умножением на мнимую единицу) с последующей нормировкой функцией , более интересные варианты получаются заданием её явным образом, в простейшем случае — нормалью к окружности.
2) явно задать внутреннюю и внешние огибающие, а конкретную точку между ними находить интерполяцией всё той же синусоидой. Этот вариант чуть сложнее, зато более предсказуемый.
Начнём с простого:
Обратите внимание: здесь мы не использовали синусоидную ленту — а обошлись лишь одной синусоидой, с некратным периодом 8/5. Для того, чтобы она замкнулась, потребовалось 5 полных оборотов (да, совпадение со знаменателем периода не случайно). Также обратите внимание, что направляющая для синусоиды не перпендикулярна центральной линии — потому что это условие в неё и не закладывалось. А если мы захотим его заложить — то потребуется продифференцировать кривую и повернуть её на 90° умножением на мнимую единицу:
Как видно, получился тоже эллипс, только с другим масштабом (и сдвигом фазы на 90° что в нашем случае значения не имеет). Используя эту функцию (с коррекцией масштаба) в качестве направляющей для синусоидной ленты получим следующую формулу:
Последний штрих — нормировать длину направляющей к единице, чтобы ширина заполняющей ленты была одинаковой (или явно заданной амплитуды). Сделать это можно функцией или, что то же самое, через деление на абсолютное значение (которое считается как квадратный корень суммы квадратов мнимой и действительной части).
Читайте также:


