Тон шепарда как сделать
Оно же в английской Википедии - тут вот можно послушать пример шепардовского нисходящего глиссандо. Правда, понятно, это само по себе не совсем то, что я имел в виду - то есть, таким образом оформленные звуки, уходящие по октавам в бесконечность вверх и вниз за границы слышимости - это только базовая технология. С её помощью можно строить как такие фрагменты, в которых будет прослеживаться чёткая мелодия (как в этом глиссандо, которое, разумеется, однозначно определяется как нисходящее, без всяких сомнений - или же если одноголосная мелодия будет ходить по небольшим, узким интервалам), а вот если ходить в основном по квартам и квинтам ("одним" голосом, если тут уместно такое выражение) или же практически как угодно ходить, но трёх- или более-звучными аккордами (ну, только что не ездить малыми секундами одним аккордом, а как-то там менять аккорды более-менее традиционными гармоническими схемами) - то (как мне кажется) прослеживать мелодию станет совершенно невозможно, т.к. будет не только не видно верхнего, ведущего голоса, но и не будет однозначного слышания относительного хода мелодии, т.е. является ли новая нота переходом вверх или вниз от какой-то из соседних старых нот. В то время как гармония-то остаётся в полном объёме, т.к. куда ж она денется. В общем, теперь хотя бы какие-то ссылки появились, более-менее понятно, что и по каким ключевым словам теперь копать.
Каким образом это возможно? Чтобы одноименная нота в разных октавах звучала одинаково?
Каким образом отсутствие обращений следует из предыдущего высказывания? Ну разве что мы оперируем только звуками одной октавы, тогда они будут выставляться только в одном возможном порядке. Чего ради?
В целом создалось впечатление, что вышеупомянутая "гармония без мелодии" будет больше всего напоминать обычный шум. Почти как в анекдоте: удовольствия никакого, но за перформанс выдать можно.
Ну вот, собственно, наконец-то появился у нас в руках материал, позволяющий как-то более предметно ответить на эти и подобные вопросы. Мне и самому очень интересно послушать всяких примеров такого плана, именно таких вот, не на коленке, а нормально, грамотно сделанных и точно отстроенных, чтоб без всяких там ступенек, скачков и прыжков, заметных на слух, но только сейчас что-то спать хочется, однако.
http://www.youtube.com/watch?v=DfJa3IC1txI
Ну вот, удалось нарыть звуковую иллюстрацию на ютубе (английская Википедия требует какого-то дополнительного плеера).
Забавно, но что дальше-то с этим делать? Слушать как есть и наслаждаться? Проиллюстрировать пару эпизодов "про космос" в кино и игрушках?
Мое мнение почти не изменилось:
В целом создалось впечатление, что вышеупомянутая "гармония без мелодии" будет больше всего напоминать обычный шум. Почти как в анекдоте: удовольствия никакого, но за перформанс выдать можно.
Это, конечно, поблагозвучнее шума, этакое синтезаторное подвывание. Оно так и звучит все время "одним цветом" или можно менять звуковысотность? Если можно, то мелодийку а-ля звездные войны сочинить удастся. Если же эта "сирена" просто существует как феномен - то она просто курьез, применительно к музыкальной практике. И любопытный научный эксперимент.
Забавно, но что дальше-то с этим делать? Слушать как есть и наслаждаться?
Видимо, всё-таки делать самому по-настоящему. Т.е. чтобы был инструмент, которым можно было бы сыграть что-нибудь. Наверное, самое удобное - это наделать сэмплов, а сэмплы уже можно загрузить в стандартную музыкальную программу, и заставлять её играть хоть по нотам, хоть вживую с подключённой MIDI-клавиатуры. Ибо этот пример - это только сугубо частный пример, причём, как выясняется при ближайшем рассмотрении - довольно грубо и кустарно сделанный. Хотя для достижения желаемого для данного примера эффекта и этого достаточно, но всё-таки интереснее было бы сделать по-настоящему.
Оно так и звучит все время "одним цветом" или можно менять звуковысотность? Если можно, то мелодийку а-ля звездные войны сочинить удастся.
Хм, вот как раз в этом примере звуковысотность вообще всё время меняется, прямо-таки непрерывно. Тон всё время ползёт вниз, в данном случае. Да, в данном случае (в общем-то это и на слух понятно) звучит не одна нота, а минорное трезвучие. И вот это минорное трезвучие ползёт вниз. За весь ролик тон таким постепенным образом опускается на 3 октавы. На 3 октавы! А вы спрашиваете, можно ли менять звуковысотность
Это, конечно, поблагозвучнее шума, этакое синтезаторное подвывание.
Ну а если взять и на 3 виолончелях просто по всему грифу так вот постепенно проехаться минорным или мажорным трезвучием - там это потянет на 2 октавы, если использовать только одну струну на каждой виолончели - это что, будет сразу музыка с большой буквы? Или если на органе взять одно трезвучие и этим ограничиться - это будет музыка? В данном случае мы имеем пример, который создан для демонстрации принципа (бесконечного непрерывного понижения тона "по кругу"), а не в качестве выдающегося музыкального произведения. Хотя, надо сказать, что-то музыкальное из этого всё-таки получилось. В значительной степени из-за того, что там звучат не простые синусоиды, а обработанные неким вкусным спецэффектом (когда мощность как-то псевдослучайно гуляет между нотами, за счёт чего звук получается переливчатым - но это не связано напрямую с принципом Шепарда, т.е. точно такую же обработку применяют для самых обычных электроорганных тембров, и получают такой же эффект - т.е. это просто такое произовольное тембровое украшение). Чистые синусоиды без спецэффекта, конечно, звучали бы намного скучнее (хотя искомый эффект всё равно бы показали). Можно в качестве основы взять и не синусоиду, а любой тембр, какой понравится - натуральный или синтезированный. С точки зрения музыки вообще и гармонии в частности это даже почти необходимо, т.к. в аккордах ноты связаны друг с другом через обертоны, а у синусоиды как раз обертонов и нет, поэтому на них гармония получается почти чисто формальная, без мощной физической основы. Т.е. для человека чувствуется только через всякие тонкие психоакустические эффекты и нелинейность слухового тракта, который всё-таки как-то искажает синусоиду и даёт пусть слабые, но хоть какие-то обертоны, на которых в голове человека уже что-то строится.

Наконец, почему я говорю, что пример кустарный и не соответствующий на самом деле заявленным принципам, и является лишь имитацией (хотя и неплохо выполняющей свою демонстрационную роль в частном случае):
Отсюда видно, и на самом деле можно достаточно точно представить себе, каким образом автор создавал эту запись. Видно, что одновременно начинают и заканчивают звучать почему-то все 3 звука аккорда в явно видном определённом, "нулевом" обращении. При том, что они имеют, естественно, разную частоту. Т.е. что скорее всего сделал автор:
1) в редакторе создал логарифмически падающую по частоте (т.е. равномерно падающую по музыкальной высоте тона) синусоиду, спускающуюся на 3 октавы;
2) сделал 2 копии оной в отдельных дорожках, и просто поднял их на 3 и 7 полутонов вверх, например (или на 4 и 7 вниз, или одну на 3 вниз, другую на 4 вверх), получив таким образом минорный аккорд, спускающийся на 3 октавы;
3) применил к этим дорожкам по отдельности или уже вместе тот самый вкусный спецэффект (это уже техническая подробность того, каким образом этот спецэффект работает), получив аккорд с красивым переливчатым звуком;
4) опять же сделал, скажем, 7 копий дорожки с аккордом, и сместил их по времени "лесенкой" с шагом на треть длины записи, т.е. так, чтобы каждый следующий заход отстоял по высоте на октаву от предыдущего;
5) просто вырезал искомое из середины, где все октавы уже и ещё заполнены, и сделал плавное вступление и затухание для красоты.
Вообще говоря, это неправильно. Ибо нота там должна "выплывать" из тишины и уходить в неё только по критерию входа-выхода в некий заранее назначенный частотный диапазон условной слышимости, но никак не исходя из своего положения в аккорде. Т.е. как минимум иначе следовало делать второй шаг - надо было смещать ноты не вверх/вниз на нужную высоту, а тоже только во времени на такие расстояния, которые обеспечат нужные для аккорда интервалы. И тогда бы мы не имели на спектрограмме таких здоровенных "зубьев" высотой в целую октаву, а имели бы ноты, которые появляются и исчезают всё время на одной частоте. И соответственно вместе с зубьями исчезнут и последние остатки некой избранности "нулевого обращения" аккорда перед другими обращениями.
Но это тоже не будет вполне правильно, поскольку вообще-то желательно покрывать весь диапазон слышимых частот, и, хоть и снижая постепенно мощность, но доходить до границ слышимости. Таким образом делая для слушателя совершенно непрозрачным, отчего прервался тот или иной звук - из-за того, что он действительно прервался, или просто ушёл за границу слышимости. Диапазон же 60-1200 Гц из примера - это в общем-то детский сад, это всего 4 октавы. И обе границы - в области прекрасной слышимости. Тут надо было бы хотя бы от 10 до 12000 Гц покрывать - т.е. около 10 октав с небольшим, если делать по-честному и аккуратно.
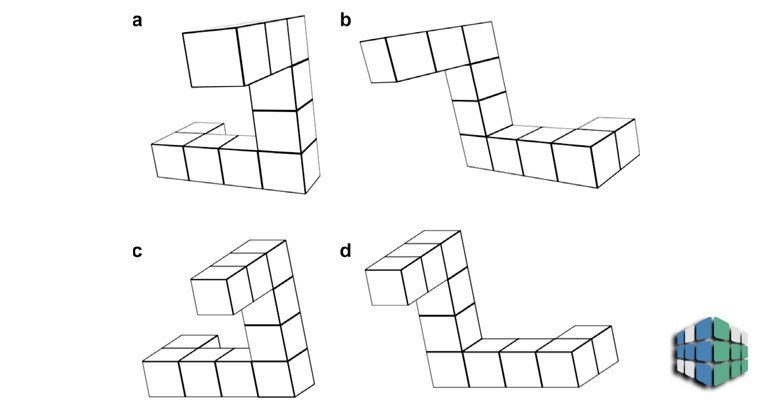
Одним из самых интересных экспериментов на восприятие является тест Роджера Шепарда, доказывающий, что человек может определить, имеют ли трехмерные объекты, изображенные на плоском рисунке, одинаковую форму, причем даже тогда, когда они представляются в различных ракурсах. Как и следует из названия, разработчиком теста является Роджер Шепард.
Роджер Шепард – американский когнитивист и психолог, получивший широкую известность благодаря своим исследованиям в области пространственных репрезентаций, таких как иллюзии восприятия и ментальное вращение. Также он изобрел звуковую иллюзию, известную как тон и лад Шепарда, и активно изучает проблему НЛО. При этом он, кстати, считает, что данная проблема должна исследоваться с точки зрении психологии, а не физики.
Значение теста Шепарда
На протяжении двух последних десятилетий психология познавательных процессов активно изучала проблему внутренней репрезентации информации о пространственных свойствах объектов. Внутреннюю репрезентацию следует понимать, как содержание, структуру и организацию знаний о мире.
Основная задача в этом случае – определить тип и степень соответствия представлений человека об объектах его внутренним операциям (с одной стороны) и реальности окружающего мира (с другой стороны).
Ученые разделились на два лагеря. Первые убеждены, что внутренняя репрезентация имеет аналоговую природу, согласно которой в сознании человека хранятся точные копии трехмерных объектов и он может манипулировать ими, как угодно. Вторые считают, что природа внутренней репрезентации является дискретной, т.е. все объекты существуют в сознании в виде символов.
Заметим также, что сторонники аналоговой гипотезы склоняются к прямому поэлементному переходу структуры внешних явлений в структуру внутренней репрезентации. А сторонники дискретной убеждены, что для обработки информации достаточно символов и никаких вспомогательных операций она не требует (естественно, это объяснение нами упрощенно).
Тест Шепарда и был предназначен, чтобы выяснить природу внутренней репрезентации, ведь по мнению ученых, структуру умственных операций можно с высокой долей точности определить по времени, затрачиваемому человеком на решение специальной пространственной задачи.
Проведенные исследования и многочисленные эксперименты (а также их модификации) позволили сделать аргументированные выводы в пользу аналоговой природы внутренней репрезентации.
Время установления соответствия или несоответствия фигур зависело от угла поворота этих фигур относительно друг друга. Это и послужило предпосылкой для вывода, что задачи решаются посредством мысленного вращения образа фигуры для его сопоставления с другой фигурой.
Ученые утверждают, что процесс внутренней репрезентации проходит несколько шагов, которые проходит и процесс внешней интерпретации. Таким образом, сохраняется поэлементное соответствие внешнему процессу ротации фигур.
Польза теста Шепарда
Тест Шепарда полезен не только для ученых, но и для обычных людей. Во-первых, умственное вращение объектов играет немалую роль в жизни человека, ведь многие профессии требуют от него выполнения пространственных задач. С помощью тестов можно определить, какие стратегии использует человек для их решения и насколько они эффективны.
Во-вторых, навык умственного вращения необходим и для решения разного рода задач в учебе. Это значит, что его развитие в той или иной степени может повлиять на то, насколько успешно будет учиться ребенок. Поэтому специалисты рекомендуют родителям время от времени проводить для детей соответствующее тестирование самостоятельно.
Несмотря на то, что результаты теста Шепарда не дают никаких конкретных описаний стратегий при выполнении задач на мысленное вращение объектов, все же можно сделать вывод, что подобные задания развивают когнитивные способности. Поэтому на их основе разрабатываются программы по тренировке и развитию мозга.
Авторизуясь в LiveJournal с помощью стороннего сервиса вы принимаете условия Пользовательского соглашения LiveJournal
Самый сок!
всё то интересное в сети, что попало в мои сети
Проверь себя
Тон Шепарда- это звук, образуемый наложением синусоидальных волн, частоты которых кратны друг другу (звуки расположены по октавам). Такой звукоряд создает иллюзию бесконечно повышающегося или понижающегося тона, в то время как на самом деле его высота в целом не меняется.
Психологами установлено, что каждый конкретный человек слышит в тоне Шепарда или только повышение, или только понижение. Во времена Первой Мировой Войны британские новобранцы проходили тест на тон Шепарда- тех, кто слышал повышающийся тон, в армию не брали. Считается, что такие люди склонны к шизофрении, немотивированной агрессии и суициду. Здоровый человек слышит понижающийся тон.
Информация об этом журнале
- Цена размещения 1 000 жетонов
- Социальный капитал 13 437
- В друзьях у
- Длительность 10 часов
- Минимальная ставка 1 000 жетонов
Тон Шепарда, названный так по фамилии его создателя Роджера Шепарда, — это звук, образуемый наложением синусоидальных волн, частоты которых кратны друг другу (звуки расположены по октавам). Повышающийся или понижающийся тон Шепарда называется звукорядом Шепарда. [1] Такой звукоряд создает иллюзию бесконечно повышающегося или понижающегося тона, в то время как на самом деле его высота в целом не меняется.


Акустическая иллюзия может быть создана путём наложения серии восходящих или нисходящих последовательностей звуков (см. рис. 1). В наглядном виде конструкция выглядит так: каждый квадрат на рисунке изображает ноту. Квадраты, расположенные один над другим — это один тон Шепарда. Ноты, звучащие одновременно, находятся на расстоянии октав друг от друга. Цвет каждого квадрата отображает громкость ноты. Фиолетовый цвет соответствует самой маленькой громкости, зелёный — самой большой. Громкости распределены по нормальному закону, где вершина колокола гауссовой кривой находится в районе ноты до 5 октавы. Каждая последовательность звуков плавно вступает и плавно затихает, так что на фоне звучания других последовательностей уловить её начало и конец, не имея хорошо развитого музыкального слуха, почти невозможно. Описанный лад Шепарда с дискретными звуками (нотами) называется дискретным ладом Шепарда. Иллюзия более убедительна, если между нотами остаются небольшие паузы (отрывистое исполнение, стаккато, вместо слитного легато). Жан Клод Рисе впоследствии создал версию лада с непрерывным изменением высоты звуков Шепарда, получившую название непрерывного лада Рисе или глиссандо Шепарда — Рисе . При правильном исполнении оно создает иллюзию непрерывно повышающегося или понижающегося тона. Рисе также создал похожую иллюзию с непрерывно ускоряющимся или замедляющимся ритмом. [2]
Золотая секвенция и лад Шепарда на квинтовой цепи звуков

При разложении золотой секвенции натурального минора а также круговой прогрессии натурального мажора на квинтовую цепь, наблюдается нисходящий лад Шепарда создающий иллюзию постоянного минорного движения вниз по квинтовой цепи. [4]
Читайте также:


