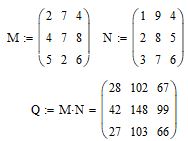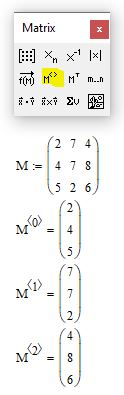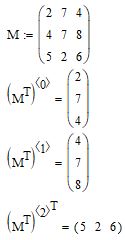Склеить матрицы в маткаде
ü осуществить действия над матрицами в среде MathCAD.
Обеспечение работы:
ü ПК с установленными необходимыми программами для работы (MathCad);
ü методические указания к выполнению работы (электронный вариант).
Порядок выполнения работы:
1. Ознакомиться с теоретическим материалом данных методических указаний;
2. Выполнить задания, приведенные в разделе II. Порядок выполнения работы;
3. Ответить на контрольные вопросы, сделать выводы.
4. Оформить отчет.
Содержание отчета:
ü тема, цель и порядок выполнения работы;
ü привести выполненные задания (скриншоты);
ü ответы на контрольные вопросы;
Теоретические положения
I. СОЗДАНИЕ ВЕКТОРОВ И МАТРИЦ В MATHCAD
В пакете MathCAD кроме матриц имеется особый класс переменных, который часто используется для замены так называемых управляющих структур (циклов). Этот класс носит название дискретные переменные. Эти переменные задаются двумя способами.
Способ 1. Используется для задания фиксированных целочисленных значений. Шаблон имеет вид:
Name := Nbegin .. Nend,
åv –получить сумму элементов,
x y × –скалярное произведение векторов,
x´y –векторное произведение векторов.
Система MathCAD также представляет большое количество функций для работы с векторами и матрицами. Воспользоваться этими функциями можно с помощью мастера функций f(x).
На рис. 2.4 представлены вычисления с использованием операций над матрицами.

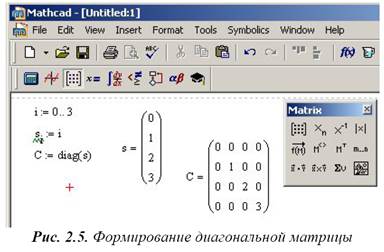
Пример 2.3.Требуется сформировать диагональную квадратную матрицу с(6x6). Значения элементов главной диагонали должны совпадать с номером строки/столбца.
Решение. Для получения диагональной матрицы в системе предусмотрена функция diag, которая имеет один параметр – вектор диагональных элементов. Поэтому формирование матрицы начинается с создания вспомогательного вектора, в который занесем элементы для диагонали. Для формирования этого вспомогательного вектора (например, с именем s), воспользуемся вспомогательной переменной, которая будет играть роль индекса (например, i). Тогда формирование диагональной матрицы может быть получено в результате операций, как это показано на рис. 2.5.
Решение. Для соединения двух матриц в одну матрицу можно использовать функцию augment, параметрами которой будут являться имена соединяемых матриц, как это показано на рис. 2.6.

Пример 2.5.Даны две матрицы A с размерностью 2.3 и В с размерностью 3.3. Требуется объединить эти матрицы в одну матрицу С(5.3), так чтобы в новой матрице в качестве первых строк располагались строки матрицы А, а за ними должны следовать строки матрицы В.

Пример 2.6.Дана матрица A с размерностью 5.5. Требуется получить из этой матрицу подматрицу, в которую включить элементы, расположенные в строках, начиная с номера 2 по номер 4, и столбцах, начиная с номера 0 по номер 5.
Решение. Для выделения подматрицы с номерами столбцов и строк представленными граничными значениями предусмотрена функция submatrix. Эта функция имеет пять параметров: имя матрицы, из которой производится выбор; начальный номер строки выбора; конечный номер строки выбора; начальный номер столбца выбора; конечный номер столбца выбора. Возможное решение представлено на рис. 2.8.

Пример 2.7.Дана матрица A(3.3). Требуется получить из заданной матрицы A два вектора. Первый вектор B должен совпадать с четвёртым столбцом матрицы А, второй вектор С – с третьей строкой матрицы А.

Пример 2.8.Из матрицы А(6.6) выделить минор, который образуется в результате вычеркивания из этой матрицы нулевой строчки и третьего столбца.
Решение. Решение задачи можно свести к соединению двух подматриц, выделенных из матрицы А, как это показано на рис. 2.10.
Использование матриц специального вида для выполнения матричных операций в системе MathCAD. Известно, что в результате умножении матрицы на вектор получается вектор. Причем, каждый i-й элемент этого вектора-результата представляет собой сумму попарных произведений соответствующих элементов i-й строки матрицы на элементы вектора-сомножителя. Очевидно, если в векторе, на который умножается матрица, все элементы равны нулю, а один элемент равен единице, то результатом такого произведения будет число, соответствующее тому элементу i-ой строки матрицы, где векторным сомножителем будет единица. Такой вывод можно использовать для выделения (формирования) из матрицы нужного столбца.
Пример 2.9.Дана матрица A(4x4). Требуется получить из этой матрицу два вектора. Первый вектор должен совпадать с нулевым столбцом матрицы А, а второй – с 3-м столбцом матрицы А.
Решение. Для получения новых векторов сформируем два вспомогательных вектора: вектор B1– с единичным значением в строке с номером 0, а второй вектор В2 – с единичным значением в строке с номером 3. Тогда для получения векторов в соответствии с условием задачи достаточно умножить матрицу А справа на векторы В1 и В2, как это показано на рис. 2.11.

Аналогичным образом можно получить вектор-строку из матрицы. Для этого достаточно сформировать вспомогательный вектор-строку, у которой все компоненты равны нулю, а одна компонента, номер которой соответствует номеру выделяемой строки из матрицы, равна единице. Если этот вектор умножить слева на матрицу, то в результате будет получена нужная строка.
Пример 2.10.Дана матрица A(4.4). Требуется переставить в матрице строки с номерами 0 и 1.
Решение. Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в строках должно соответствовать нужному порядку для расположения строк в новой матрице. После этого решение можно получить простым перемножением матриц (рис. 2.12).

Пример 2.11.Дана матрица (4.4). Требуется найти сумму элементов в третьем столбце матрицы.
Решение. Для решения задачи требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение (рис. 2.13).

Пример 2.12.Дана матрица: A(4.4). Требуется получить вектор, элементы которого будут представлять суммы элементов в столбцах матрицы.
Решение. Для решения требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение (рис. 2.14).

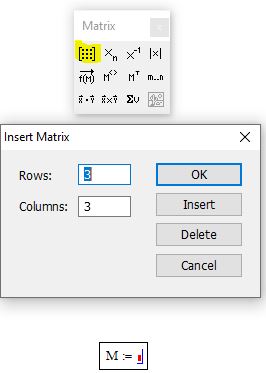
Чтобы ввести матрицу в mathcad 15 нужно в свободном поле ввести с клавиатуры имя матрицы. Пусть это будет M. Затем на панели Matrix нужно нажать кнопку "Matrix or vector". В появившемся окне нужно ввести количество строк и столбцов и нажать OK
Рис. 1. Ввод матрицы
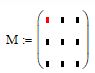
Затем появится заготовка матрицы с пустыми маркерами для ввода элементов вручную. См. рис. 2
Рис. 2. Заполнение матрицы
Перемножение матриц
Как известно, перемножение матриц осуществляется по правилу "строка на столбец". Введем 2 матрицы 3 х 3 с именами M и N. Перемножение матриц осуществляется с помощью стандартной операции умножения. На рис. 3 смотрите синтаксис записи
Рис. 3. Перемножение матриц
Транспонирование матриц
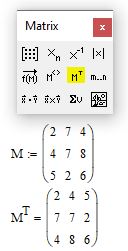
Как известно, при транспонировании матрицы ее строки становятся столбцами. В mathcad есть функция, которая позволяет выполнить транспонирование. Введите имя матрицы, которую хотите транспонировать, и на панели Matrix нажмите кнопку "Matrix transpose". На рис. 4 смотрите синтаксис для записи этой операции.
Рис. 4. Транспонирование матрицы
Обратные матрицы
Как известно, обратной матрицей M^-1 является такая матрица, при умножении которой на исходную матрицу M получается единичная матрица. Существует множество аналитических способов нахождения обратной матрицы. В mathcad есть стандартная операция по определению обратной матрицы. Введите исходную матрицу M. Затем снова введите имя матрицы M и на панели Matrix нажмите кнопку "Invers". на рисунке 5 можно посмотреть синтаксис записи и убедиться в правильности определения обратной матрицы
Рис. 5. Обратная матрица
Выделение столбца и строки из матрицы
Для того чтобы "вытащить" столбец из матрицы можно воспользоваться стандартной функцией mathcad из панели matrix. Введите произвольную матрицу M и затем ниже в рабочем поле mathcad выполните операцию, как показано на рис. 6. Обратите внимание, что по умолчанию номера столбцов и строк индексируются с "нуля"
Рис. 6. Выделение столбца матрицы
Аналогичным способом можно выделить строку, но для этого матрицу предварительно нужно транспонировать. При этом строка будет отображена в виде столбца. Если вы хотите получить результат в виде строки, то операцию транспонирования нужно провести 2 раза. Синтаксис будет выглядеть как на рисунке 7
Рис. 7. Выделение строки матрицы
Обратите внимание, что если при перемножении матриц их размерность "не совпадает" то mathcad выдаст ошибку
Обратите внимание, что обратная матрица не всегда может существовать для исходной матрицы

Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.
Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.
Рассмотрим простейшие операции матричной алгебры, реализованные в MathCAD в виде операторов, причем следует отметить, что их запись максимально приближена к математической форме записи. Наиболее часто используемые операции расположены на панели инструментов Матрица (Matrix) (рис. 13), остальные можно найти используя меню Вставка → Функция… категории функций Vector and Matrix.


Рис. 6.13. Панели инструментов Матрица и Логика
Транспонированием называют операцию, переводящую матрицу размерности M×N в матрицу размерности N×M, делая столбцы исходной матрицы строками, а строки - столбцами. Ввод символа транспонирования (transpose) осуществляется с помощью панели инструментов Матрица(Matrix) или нажатием клавиш + . Не забывайте, что для вставки символа транспонирования матица должна находиться между линиями ввода.
При умножении следует помнить, что матрицу размерности M×N допустимо умножать только на матрицу размерности N×P (P может быть любым). В результате получается матрица размерности M×P.

Чтобы ввести символ умножения, нужно нажать клавишу со звездочкой или воспользоваться панелью инструментов Матрица (Matrix), нажав на ней кнопку Dot Product (Умножение). Умножение матриц обозначается по умолчанию точкой.
Для получения сведений о характеристиках матриц или векторов предусмотрены следующие встроенные функции:
· rows (A) - число строк;
· cols (A) - число столбцов;
· length(v) - число элементов вектора;
· last (v) - индекс последнего элемента вектора,
где A - матрица или вектор; v - вектор.

Скалярное произведение векторов (vector inner product) определяется как скаляр, равный сумме попарных произведений соответствующих элементов. Векторы должны иметь одинаковую размерность, скалярное произведение имеет ту же размерность. Скалярное произведение двух векторов u и v равно , где - угол между векторами. Если векторы ортогональны, то их скалярное произведение равно нулю. Обозначается скалярное произведение тем же символом, что и умножение.

Векторное произведение (cross product) двух векторов u и v с углом между ними равно вектору с модулем , направленным перпендикулярно плоскости векторов u и v. Обозначают векторное произведение символом , который можно ввести нажатием кнопки Cross Product(Векторное произведение) в панели Матрица(Matrix) или сочетанием клавиш + .

Определитель матрицы обозначается стандартным математическим символом. Чтобы ввести оператор нахождения определителя матрицы, можно нажать кнопку Determinant (Определитель) на панели инструментов Матрица(Matrix) или набрать на клавиатуре (нажав клавиши + ).
Рангом (rank) матрицы называют наибольшее натуральное число k, для которого существует не равный нулю определитель k-го порядка подматрицы, составленной из любого пересечения k столбцов и k строк матрицы. Для определения ранга матрицы в MathCAD используется функция rank(A), где А - матрица, ранг которой требуется найти.

Как известно, поиск обратной матрицы возможен, если матрица квадратная и ее определитель не равен нулю. Произведение исходной матрицы на обратную по определению является единичной матрицей. Для ввода оператора поиска обратной матрицы нажмите кнопку Инверсия (Inverse) на панели инструментов Матрица(Matrix).
В линейной алгебре используются различные векторные и матричные нормы (norm), которые ставят в соответствие матрице некоторую скалярную числовую характеристику. Норма матрицы отражает порядок величины матричных элементов. В разных специфических задачах линейной алгебры применяются различные виды норм. MathCAD имеет четыре встроенных функции для расчета разных норм квадратных матриц:
· norm1(A) - норма в пространстве L1;
· norm2 (А) - норма в пространстве L2;
· norme (A) - евклидова норма (euclidean norm);
· normi (A) — max-норма, или -норма (infinity norm):
где A - квадратная матрица.
Часто бывает нужно переставить элементы матрицы или вектора, расположив их в определенной строке или столбце в порядке возрастания или убывания. Для этого имеются несколько встроенных функций, которые позволяют гибко управлять сортировкой матриц:
· sort(v) - сортировка элементов вектора в порядке возрастания;
· reverse (v) - перестановка элементов вектора в обратном порядке;
· csort(A, i) - сортировка строк матрицы выстраиванием элементов i-столбца в порядке возрастания;
· rsort(A,i) - сортировка столбцов матрицы выстраиванием элементе i-й строки в порядке возрастания, где v - вектор; А - матрица; i - индекс строки или столбца.
Примеры работы рассмотренных выше операторов представлены на рис. 6.14.

Рис. 6.14. Работа с матрицами в MathCAD
Для задания логических функций в MathCAD имеется панель инструментов Логические (Boolean) рис. 6.13. На ней расположены кнопки, отражающие отношения (=, >,
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
С этими понятиями Вы могли сталкиваться, работая в Excel – столбец чисел называется вектор-столбцом, строка – вектор-строкой. Блок объектов является матрицей. Вычисления в Excel, по сути, являются операциями с векторами и матрицами. В этом уроке мы познакомимся с аналогичными вычислениями в Mathcad, и мы поймем, почему в Mathcad их проводить проще.
Введение

Это значение можно вывести прямо в документ, чтобы не забыть его и не запутаться:
Теперь рассмотрим несколько матриц:

Как видно, они могут включать в себя числа, символы и даже функции. Они также могут содержать текстовые элементы (строки).
Элемент матрицы можно вывести, используя подстрочные индексы:

Матрицы выше являются квадратными 2х2, но у них может быть любой размер по строкам и столбцам:

Запомните: первое число – номер строки (или их количество), второе – столбца.
Элементы, выделенные с помощью подстрочных индексов:

Для вектор-столбца второй индекс можно опустить, но не для вектор-строки:

Во вкладке Математика –> Операторы и символы –> Операторы –> Векторы и матрицы Вы найдете команды для выделения столбцов и строк:


Многие операции для векторов и матриц аналогичны операциям для обычных чисел, переменных и функций: сложение, вычитание, некоторые виды умножения. Поиск обратной матрицы близко к операции деления. Вы можете записать эти операторы, используя имена векторов и матриц. В качестве примера рассмотрим векторное произведение матрицы и вектора:
Мы рассмотрим эту операцию подробнее позже. Однако стоит заметить, что она требует девять операций умножения и девять – сложения. Расписывать их утомительно и чревато ошибками – для больших матриц сделать это очень трудно.
Применение векторов очень широко. Вспомните пиксели на экране монитора – их могут быть миллионы. Они обрабатываются с помощью операций с матрицами.
В Mathcad

Перемести указатель на сетку, выберите желаемый размер матрицы, затем щелкните левой кнопкой мыши. Появится пустая матрица:
Матрице можно присвоить имя, щелкнув на левую скобку, нажав [:] для оператора присваивания и введя имя:

Операции с матрицами
Эффект от различных операций с матрицами и векторами будет проще понять, используя символы. Будем использовать две матрицы и два вектора:

Оператор транспонирования находится на вкладке Математика –> Операторы –> Векторы и матрицы:

Щелкните по правой границе матрицы и примените оператор. Он работает как для символьных, так и для числовых матриц:

Часто операции в векторами приходится совершать поэлементно. Для этого служит оператор векторизации. Операции в Excel зачастую являются поэлементными, они также важны и в Mathcad. Чтобы перемножить два вектора поэлементно, сначала введите простое умножение:
Затем выберите все выражение и примените векторизацию:
Вычислите, чтобы посмотреть результат: первый элемент умножается на первый, второй – на второй, и т.д.:
Другие поэлементные операции:

Поэлементные операции применимы только к массивам одного размера.
Сложение и вычитание
Сложение и вычитание выполняется поэлементно:

Эта операция также применима лишь к массивам одного размера.
С помощью оператора суммирования можно найти сумму всех элементов вектора (не матрицы):
Умножение на константу работает так:

При скалярном умножении матриц происходит умножение строк на столбцы. При этом используется тот же символ, что и при обычном умножении. Эта операция допустима только для тех матриц, в которых число строк в первой матрице равно числе столбцов во второй. Для наших матриц 2х2:

Заметьте, что последовательность множителей играет роль:

Скалярное произведение не коммутативно, за исключением особых случаев:
Скалярное произведение двух векторов дает результат с комплексно-сопряженными числами (с чертой сверху). Для действительных чисел на это можно не обращать внимания:

Этот оператор применим только для двух вектор-столбцов, состоящих из трех элементов:

Векторное произведение имеет широкое применение в механике, гидродинамике, электромагнетизме и в других областях.
Обратная матрица определяется только для квадратных матриц:

Произведение матрицы и ее обратной матрицы является единичной матрицей:

Произведение матрицы и единичной матрицы дает изначальную матрицу:


Определитель можно найти только для квадратной матрицы. Его значение может быть равно нулю, даже если все элементы матрицы не равны нулю. Обратная матрица содержит дроби, в знаменателе которых находится определитель:

Если определитель равен нулю, обратной матрицы не существует, а матрица является сингулярной. Вспомните деление на ноль в обычной алгебре. Mathcad сообщит, если матрица является сингулярной:
Читайте также: