Разрежь данную фигуру на 4 равные части как это сделать покажи на чертеже в тетради
Презентация на тему: " Разрезать трапецию на четыре равные части Как разрезать равносторонний треугольник на 4 равные части, видно из рисунка: Если удалить верхний треугольник," — Транскрипт:
2 Разрезать трапецию на четыре равные части Как разрезать равносторонний треугольник на 4 равные части, видно из рисунка: Если удалить верхний треугольник, то оставшиеся 3 треугольника образуют трапецию: Попробуйте её разрезать тоже на 4 равные части.
4 Разрезание фигур на клетчатой бумаге На рисунке изображены две фигуры. Первую из них надо разрезать на четыре равные фигуры, а вторую на пять.
5 8 кусочков Разделите приведенную фигуру на 8 одинаковых частей. ответ
6 Получи квадрат ответ Разрежьте приведенную фигуру на 3 части и сложите из них квадрат. Решите задачу двумя способами.
7 Из двух квадратов один Имеются два квадрата 3×3 и 1×1. Разрезать эти квадраты на части, из которых можно было бы сложить один квадрат. Если вы справились с этой задачей, то попробуйте решить её в общем виде: перекроить два произвольных квадрата в один.
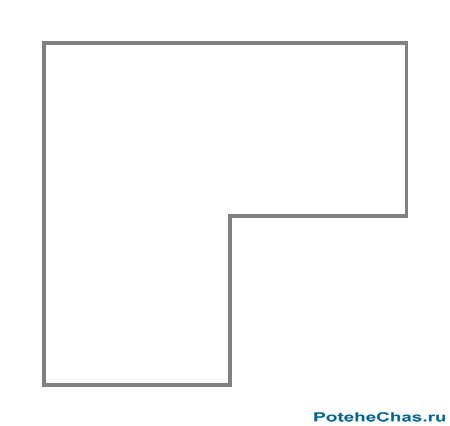
8 Разделить фигуру на равные части Попробуйте разделить данную фигуру ломаными линиями на три одинаковые части. [ Ответ на головоломку ] Ответ на головоломку
9 Разрежьте фигуру на четыре одинаковых многоугольника отличающихся по своей форме от исходной фигуры. [ Ответ на головоломку ] Ответ на головоломку
10 Квадрат Перед вами два квадрата, один из которых уже разделен на четыре одинаковых треугольника. Как при помощи этих треугольников и маленького квадрата сложить один большой квадрат? Ничего больше разрезать не требуется. [ Ответ на головоломку ]Ответ на головоломку
11 У одной из сестер милосердия, было пять кусков красной материи, из которых она, используя все эти куски и не разрезая их более, сшила крест. Как она это сделала? [ Ответ на головоломку ] Ответ на головоломку
12 Разрежьте фигуру двумя резами на четыре части и соберите их низ квадрат. [ Ответ на головоломку ] Ответ на головоломку
13 Разделите фигуру на две одинаковые части, и из полученных частей сложите шахматную доску. [ Ответ на головоломку ] Ответ на головоломку
14 Праздничный пирог разрезан на шестнадцать одинаковых квадратных кусков. Возможно ли было разрезать пирог на шесть квадратных кусков (можно даже различных размеров)? Если возможно - то каким образом это сделать? [ Ответ на головоломку ] Ответ на головоломку
15 На рисунке изображена фигура в виде запятой. При помощи одной кривой линии разделите эту фигуру на две одинаковые части. Какую геометрическую фигуру можно сложить из двух таких фигур ("запятых")? [ Ответ на головоломку ] Ответ на головоломку
16 Каким образом необходимо разрезать данный крест, чтобы из полученных кусков можно было собрать квадрат с пустотой внутри него в виде такого же по форме и размерам креста. [ Ответ на головоломку ] Ответ на головоломку
Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику

Математический кружок 6 класс
Семь раз отмерь, один отрежь!
(5 баллов) Прямоугольник 3 × 5 содержит 15 клеток и центральная клетка удалена. Найдите как можно больше способов разрезания прямоугольника на две равные части по линиям сетки. За каждый новый способ разрезания начисляется 1 балл. (Два способа мы считаем разными, если фигурки, получающиеся при первом способе разрезания, не такие, как при втором.)
( 3 балла) Можно ли квадрат 5×5 клеток разрезать на две равные части так, чтобы линия разреза шла по сторонам клеток?
(7 баллов) Разрежьте фигуру справа на 4 равные части так, чтобы линии разреза шли по сторонам клеточек. Придумайте как можно больше способов разрезания. За каждый способ начисляется по 1 баллу.
(3 балла) Разрежьте каждую из фигур, изображенных ниже, на 4 равные части.
(4 балла) Гриша утверждает, что у него есть бумажная фигурка, которую можно перегнуть одним способом — и получится квадрат; можно перегнуть другим способом — и получится равнобедренный треугольник. Не хвастает ли Гриша?
(3 балла) Разрежьте ракету на 3 каких-то части и сложите из них квадрат.
(3 балла) Разрезав фигуру на 4 одинаковые части, сложите квадрат
(3 балла) Разрежьте на 2 одинаковые по форме части фигуру
Дополнительные задачи
Разрежьте на 4 равные части
Разрежьтефигуру на 3 равные части
Разрежьте на 5 частей, одна из которых квадрат, и сложите их так, чтобы всего получилось 3 квадрата.
Разрежьте фигуру двумя прямыми линиями на 6 частей
. Разделите прямоугольник тремя прямыми линиями так, чтобы в каждой части лежала ровно одна точка
Начертите 12-угольник так, чтобы, соединив его вершины через одну, можно было получить шестиугольник, площадь которого больше, чем площадь 12-угольника, и соединив вершины через две, можно было бы получить четырехугольник, площадь которого тоже больше площади исходного 12-угольника.
Это занятие предлагается устроить в виде соревнования – начислять за задания баллы и вести счет кто больше наберет. В задачах 1 и 3 дается 1 балл за каждое разрезание, сдавать эту задачу можно постепенно. Например, ребенок может сперва придумать три способа и сдать задачу, потом придумать два новых способа и получить за них дополнительные баллы. В задачах 6 и 7 не требуется придумать как можно больше способов, однако можно накидывать дополнительный 1 балл тому, кто придумает несколько способов.
Победителю можно выдать грамоту, образец прилагается в дополнительном файле.
Решения задач
(5 баллов) Прямоугольник 3 × 5 содержит 15 клеток и центральная клетка удалена. Найдите как можно больше способов разрезания прямоугольника на две равные части по линиям сетки. За каждый новый способ разрезания начисляется 1 балл. (Два способа мы считаем разными, если фигурки, получающиеся при первом способе разрезания, не такие, как при втором.)
Ответ .
(3 балла) Можно ли квадрат 5×5 клеток разрезать на две равные части так, чтобы линия разреза шла по сторонам клеток?
Ответ . Нет, нельзя.
Решение . Т.к. мы режем по сторонам клеточек, то в каждой фигуре окажется целое число клеточек. Так как фигуры равны, то в них должно быть поровну клеточек, т.е. в сумме в этих двух фигурах должно быть четное число клеточек. А у нас в исходной фигуре 25 клеточек – нечетное число.
(7 баллов) Разрежьте фигуру справа на 4 равные части так, чтобы линии разреза шли по сторонам клеточек. Придумайте как можно больше способов разрезания. За каждый способ начисляется по 1 баллу.
Ответ .
(3 балла) Разрежьте каждую из фигур, изображенных ниже, на 4 равные части.
(4 балла) Гриша утверждает, что у него есть бумажная фигурка, которую можно перегнуть одним способом — и получится квадрат; можно перегнуть другим способом — и получится равнобедренный треугольник. Не хвастает ли Гриша?
Ответ. Нет, не хвастает. Например, у него могла быть такая фигура, линии сгиба красные.
(3 балла) Разрежьте ракету на 3 каких-то части и сложите из них квадрат.
Ответ. Например, любым из приведенных ниже трех способов
(3 балла) Разрезав фигуру на 4 одинаковые части, сложите квадрат.
Ответ. Возможные линии разрезов приведены на рисунках.
| « | К списку головоломок |
Занимательные головоломки в картинках с решениями и ответами для детей и взрослых; множество красочных головоломок для решения онлайн бесплатно; головоломки со спичками, разрезание фигур на части, на распознавание скрытых образов; тренировка сообразительности и логического мышления .
Сборник занимательных шуточных загадок, при разгадывании которых желательно не спешить с ответом, так как в большинстве случаев в ответ загадки заложен .
Занимательный геометрический материал для младших школьников 4 класса
1. Назвать одним словом: отрезок, луч, квадрат, прямая, овал, круг.
2. Разделить фигуры на две группы.
.jpg)
3. Подумай и ответь.
Как изменится площадь снежной крепости, если каждую стену достроить, увеличив в 3 раза? (В 9 раз.)
4. Решите задачи.
1) Квадратную сеть со стороной 10 м старик разрезал на квадратики со стороной 1 дм и разложил их на берегу в виде ленты в ряд. Какой длины получилась полоса?
2) Лист согнули пополам, полученный кусок бумаги еще раз. И так всего 6 раз. Распрямив лист, его разрезали по местам сгибов. Сколько всего получилось листочков? (64.)
3) Шоколадку данной формы разрезали на три равные части. Как это сделать?
.jpg)
4) Мальчик нашел легко гнущуюся проволоку длиной 1м 35 см и разрезал ее на равные части. Путем сгибания он получил равносторонние треугольники, длины сторон которых выражаются целыми числами сантиметров. Сколько таких треугольников он мог получить?
Ответ: 9 треугольников, стороны которых равны 5 см.
5) Пирог прямоугольной формы разделили на 4 части двумя разрезами так, что две из них оказались четырехугольной формы, а две треугольной. Как это сделали?
.jpg)
6) На квадратном огороде, периметр которого 80 м, посадили собаку на цепь длиной 9 м 70 см и прикрепили цепь к столбу, торчащему в самом центре огорода. Длина собаки от ошейника до передних зубов 30 см. Смогут ли пробраться в огород мыши?
1) 9 м 70 см + 30 см = 10 (м) - на данном расстоянии собака охраняет участок.
2) 80 : 4 = 20 (м) - длина огорода.
Ответ: мыши могут пробраться в огород, так как не весь участок охраняется собакой.
7) В комнате 4 угла. В каждом углу сидит кошка. Напротив каждой кошки по 3 кошки. На хвосте каждой кошки по одной кошке. Сколько же всего кошек в комнате?
8) Девять точек в углах клеток образуют квадрат. Какое наименьшее число точек можно к ним добавить, чтобы получился новый квадрат, содержащий имеющиеся точки?
.jpg)
Ответ: можно добавить 4 точки.
.jpg)
9) Две гусеницы забрались на один листок площадью 50 кв. см.
- Это мое! - грозно сказала одна из них и очертила на листе территорию 35 кв. см.
- Это мое! - сказала вторая и очертила участок такой же площади. Образовалась спорная территория. Чему равна ее площадь?
1) 50-35 = 15 (кв. см) - площадь, занимаемая каждой гусеницей.
2) 50 - (15 х 2) = 20 (кв. см) - спорная площадь.
Ответ: площадь спорной территории равна 20 кв. см.
5. В гости в сказку.
У одного царя-батюшки было 3 дочки и прямоугольное царство, одна сторона которого 60 км, а другая 74 км. Старшая вышла замуж за принца и получила в приданое полцарства, средняя вышла за воеводу, получив в приданое квадратную часть того, что осталось от царства, и периметр этого квадрата был равен 148 км. Младшая вышла замуж за Трубодура и получила площадь в 850 кв. км 999 965 кв. м. Какая площадь досталась в приданое всем трем дочкам. Какую жилплощадь оставил себе царь-батюшка?
Ответ: старшей дочери досталось 2 220 кв. км; средней - 1 369 кв. км; царю-батюшке осталось 35 кв. м.
1. Разгадать кроссворд.
1) Геометрическая объемная фигура.
2) Объемная геометрическая фигура, грани которой одинаковы.
3) Буква алфавита, не имеющая звука.
4) Чем ограничены грани объемных фигур?
5) Единица измерения длины.
— Какое ключевое слово получили? (Объем.)
.jpg)
2. Разделить фигуры на три группы.
.jpg)
3. Найти лишнюю величину в каждом ряду:
7 м, 7 км, 7 см, 7 куб. м
7 куб. м, 4 куб. см, 6 куб. см, 5 куб. мм, 17 куб. дм
5 кв. см, 500 кв. мм, 5000 куб. мм
4 кв. м, 4000 куб. дм, 400 кв. дм
4. Найти для левой части правила соответствующую часть справа:
5. Проверить, верны ли равенства:
4 куб. м = 4000 куб. дм
7 куб. дм = 700 куб. см
4 куб. дм 6 куб. см = 46 куб. см
7 куб. см 40 куб. мм = 940 куб. мм
6. Решить задачи.
1) Как набрать из водопровода 6 л воды, пользуясь двухлитровой банкой и чайником, в который входит 5 л воды?
2) Деревянный окрашенный куб с ребром 3 см распилили на кубические сантиметры. Сколько среди них кубиков, которые окрашены с трех сторон? (4 кубика.)
3) Сколько потребуется проволоки Винтику и Шпунтику, чтобы спаять каркас куба с ребром 5 см? (40 см.)
4) Три кубика, каркасы которых сделаны из проволоки, расположены, как показано на рисунке. Сколько потребовалось проволоки, если ребро куба равно 8 см? (8 х 8 х 3 = 192 см.)
.jpg)
5) В мерный стакан налили 171 куб. см воды. После того как в него опустили куб, стороны которого равны 3 см, и прямоугольную призму, в основании которой квадрат со сторонами 2 см, уровень воды в стакане поднялся до деления 222 куб. см. Чему равен объем призмы и ее высота?
1) 3 • 3 • 3 = 27 (куб. см) - объем куба.
2) 171 + 21 = 198 (куб. см) - уровень воды в стакане с кубом.
3) 222 - 198 = 4 (куб. см) - объем призмы.
4) 4 : 2 : 2 = 1 (см) - высота призмы.
Ответ: объем призмы равен 4 куб. см, а ее высота - 1 см.
1. Выписать номера фигур, распределив их на две группы:
.jpg)
2. Выбрать правильный ответ.
а) отрезок, соединяющий вершины двух любых углов многоугольника;
в) отрезок, соединяющий вершины двух углов многоугольника, не имеющие общей стороны.
Диагональ делит на два равных треугольника .
а) любой многоугольник; в) прямоугольник.
3. Дополнить: принято считать, что в прямоугольнике .
.jpg)
4. Соотнести левую и правую части правил:
.jpg)
5. Путешествие в сказку.
1) Шпунтик и его друзья из данных фигур составляли новые. Каждый из них из двух таких многоугольников, как показано на рисунке, составил новый и нашел сумму длин его сторон. Ответы у них получились разные, но у всех правильные. Как такое могло быть, и какие ответы у них получились?
Чему равны площади данных и получившихся фигур?
.jpg)
2) Незнайка из 8 цветных квадратов со стороной 1 см составил фигуру, которую наклеил на лист бумаги. Как ее теперь можно разрезать на две равные части таким образом, чтобы из них можно было бы составить прямоугольник? Чему будет равна площадь получившегося прямоугольника?
Вырежьте несколько таких прямоугольников, проведите в них диагональ.
.jpg)
Подумайте, сколько различных треугольников можно получить, разрезав прямоугольник по диагонали. Найдите площади прямоугольных треугольников.
6. Объемные фигуры.
Задание 1. Выберите фигуру, которую нужно нарисовать. Назовите данные фигуры.
.jpg)
.jpg)
.jpg)
Задание 2. Покажите грани, которые вы видите на левом и правом рисунке куба.
Задание 3. Выберите куб, который можно сделать из данной развёртки.
.jpg)
Задание 4. Выберите куб, который нельзя сделать из данной развертки.
.jpg)
Задание 5. Выберите фигуры, которые можно сделать из данной развертки.
.jpg)
Задание 6. Сколько кубиков потребуется, чтобы сложить эти фигуры?
.jpg)
.jpg)
Задание 8. Назовите номера фигур в порядке увеличения значения их объемов.
Читайте также:


