Random forest что это
Случайный лес (Random forest, RF) — это алгоритм обучения с учителем. Его можно применять как для классификации, так и для регрессии. Также это наиболее гибкий и простой в использовании алгоритм. Лес состоит из деревьев. Говорят, что чем больше деревьев в лесу, тем он крепче. RF создает деревья решений для случайно выбранных семплов данных, получает прогноз от каждого дерева и выбирает наилучшее решение посредством голосования. Он также предоставляет довольно эффективный критерий важности показателей (признаков).
Случайный лес имеет множество применений, таких как механизмы рекомендаций, классификация изображений и отбор признаков. Его можно использовать для классификации добросовестных соискателей кредита, выявления мошенничества и прогнозирования заболеваний. Он лежит в основе алгоритма Борута, который определяет наиболее значимые показатели датасета.
Алгоритм Random Forest
Итак, что вы делаете, чтобы выбрать подходящее место? Ищите информацию в Интернете: вы можете прочитать множество различных отзывов и мнений в блогах о путешествиях, на сайтах, подобных Кью, туристических порталах, — или же просто спросить своих друзей.
Предположим, вы решили узнать у своих знакомых об их опыте путешествий. Вы, вероятно, получите рекомендации от каждого друга и составите из них список возможных локаций. Затем вы попросите своих знакомых проголосовать, то есть выбрать лучший вариант для поездки из составленного вами перечня. Место, набравшее наибольшее количество голосов, станет вашим окончательным выбором для путешествия.
Вышеупомянутый процесс принятия решения состоит из двух частей.
- Первая заключается в опросе друзей об их индивидуальном опыте и получении рекомендации на основе тех мест, которые посетил конкретный друг. В этой части используется алгоритм дерева решений. Каждый участник выбирает только один вариант среди знакомых ему локаций.
- Второй частью является процедура голосования для определения лучшего места, проведенная после сбора всех рекомендаций. Голосование означает выбор наиболее оптимального места из предоставленных на основе опыта ваших друзей. Весь этот процесс (первая и вторая части) от сбора рекомендаций до голосования за наиболее подходящий вариант представляет собой алгоритм случайного леса.
Технически Random forest — это метод (основанный на подходе «разделяй и властвуй»), использующий ансамбль деревьев решений, созданных на случайно разделенном датасете. Набор таких деревьев-классификаторов образует лес. Каждое отдельное дерево решений генерируется с использованием метрик отбора показателей, таких как критерий прироста информации, отношение прироста и индекс Джини для каждого признака.
Любое такое дерево создается на основе независимой случайной выборки. В задаче классификации каждое дерево голосует, и в качестве окончательного результата выбирается самый популярный класс. В случае регрессии конечным результатом считается среднее значение всех выходных данных ансамбля. Метод случайного леса является более простым и эффективным по сравнению с другими алгоритмами нелинейной классификации.
1. Импорт данных
Для начала загрузим данные и создадим датафрейм Pandas. Так как мы пользуемся предварительно очищенным «игрушечным» набором данных из Scikit-learn, то после этого мы уже сможем приступить к процессу моделирования. Но даже при использовании подобных данных рекомендуется всегда начинать работу, проведя предварительный анализ данных с использованием следующих команд, применяемых к датафрейму ( df ):
- df.head() — чтобы взглянуть на новый датафрейм и понять, выглядит ли он так, как ожидается.
- df.info() — чтобы выяснить особенности типов данных и содержимого столбцов. Возможно, перед продолжением работы понадобится произвести преобразование типов данных.
- df.isna() — чтобы убедиться в том, что в данных нет значений NaN . Соответствующие значения, если они есть, может понадобиться как-то обработать, или, если нужно, может понадобиться убрать целые строки из датафрейма.
- df.describe() — чтобы выяснить минимальные, максимальные, средние значения показателей в столбцах, чтобы узнать показатели среднеквадратического и вероятного отклонения по столбцам.

Фрагмент датафрейма с данными по раку груди. Каждая строка содержит результаты наблюдений за пациентом. Последний столбец, cancer, содержит целевую переменную, которую мы пытаемся предсказать. 0 означает «отсутствие заболевания». 1 — «наличие заболевания»
7. Оптимизация гиперпараметров. Раунд 1: RandomizedSearchCV
После обработки данных с использованием метода главных компонент можно попытаться воспользоваться оптимизацией гиперпараметров модели для того чтобы улучшить качество предсказаний, выдаваемых RF-моделью. Гиперпараметры можно рассматривать как что-то вроде «настроек» модели. Настройки, которые отлично подходят для одного набора данных, для другого не подойдут — поэтому и нужно заниматься их оптимизацией.
Начать можно с алгоритма RandomizedSearchCV, который позволяет довольно грубо исследовать широкие диапазоны значений. Описания всех гиперпараметров для RF-моделей можно найти здесь.
В ходе работы мы генерируем сущность param_dist , содержащую, для каждого гиперпараметра, диапазон значений, которые нужно испытать. Далее, мы инициализируем объект rs с помощью функции RandomizedSearchCV() , передавая ей RF-модель, param_dist , число итераций и число кросс-валидаций, которые нужно выполнить.
Гиперпараметр verbose позволяет управлять объёмом информации, который выводится моделью в ходе её работы (наподобие вывода сведений в процессе обучения модели). Гиперпараметр n_jobs позволяет указывать то, сколько процессорных ядер нужно использовать для обеспечения работы модели. Установка n_jobs в значение -1 приведёт к более быстрой работе модели, так как при этом будут использоваться все ядра процессора.
Мы будем заниматься подбором следующих гиперпараметров:
- n_estimators — число «деревьев» в «случайном лесу».
- max_features — число признаков для выбора расщепления.
- max_depth — максимальная глубина деревьев.
- min_samples_split — минимальное число объектов, необходимое для того, чтобы узел дерева мог бы расщепиться.
- min_samples_leaf — минимальное число объектов в листьях.
- bootstrap — использование для построения деревьев подвыборки с возвращением.
При значениях параметров n_iter = 100 и cv = 3 , мы создали 300 RF-моделей, случайно выбирая комбинации представленных выше гиперпараметров. Мы можем обратиться к атрибуту best_params_ для получения сведений о наборе параметров, позволяющем создать самую лучшую модель. Но на данной стадии это может не дать нам наиболее интересных данных о диапазонах параметров, которые стоит изучить на следующем раунде оптимизации. Для того чтобы выяснить то, в каком диапазоне значений стоит продолжать поиск, мы легко можем получить датафрейм, содержащий результаты работы алгоритма RandomizedSearchCV.

Результаты работы алгоритма RandomizedSearchCV
Теперь создадим столбчатые графики, на которых, по оси Х, расположены значения гиперпараметров, а по оси Y — средние значения, показываемые моделями. Это позволит понять то, какие значения гиперпараметров, в среднем, лучше всего себя показывают.
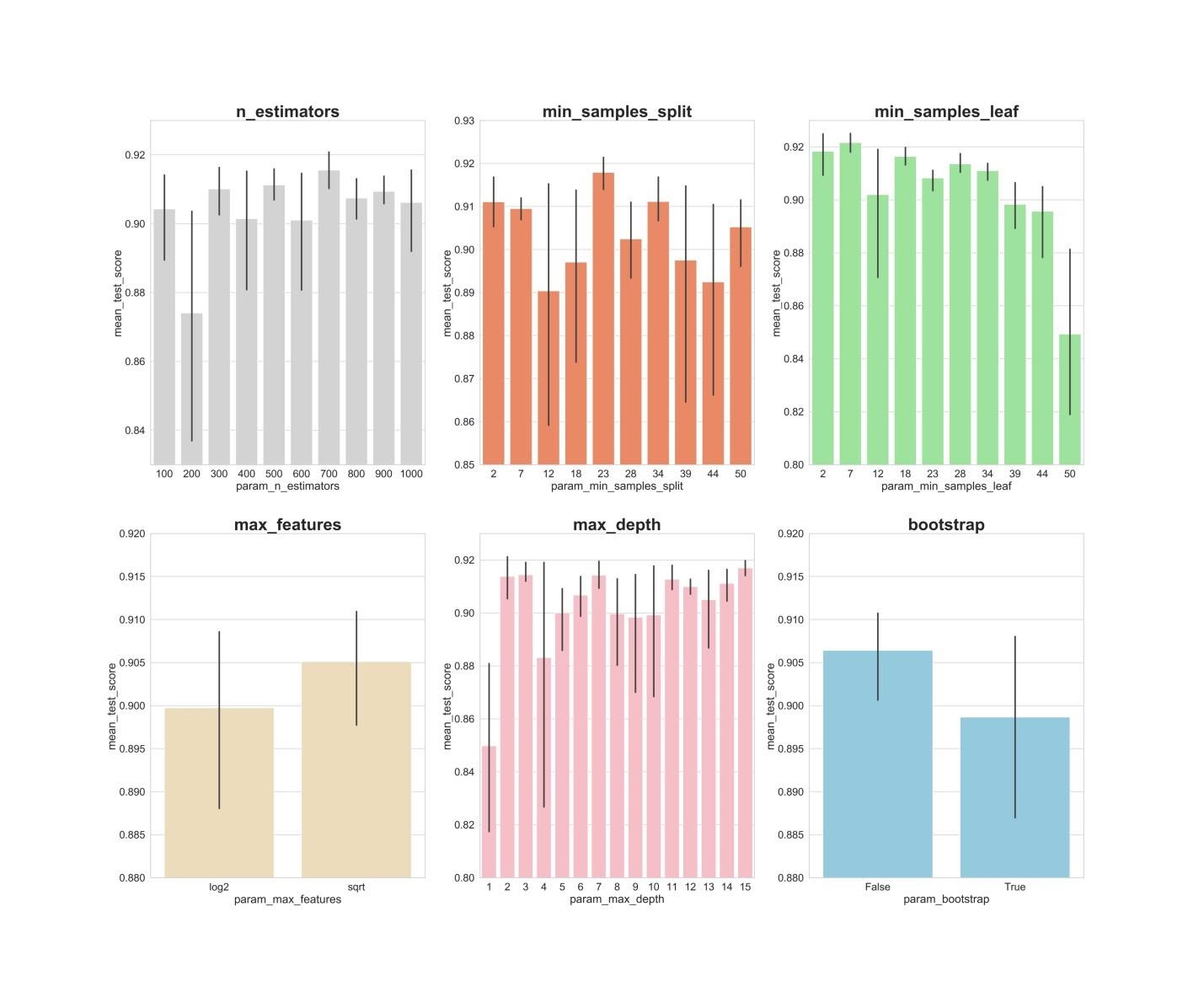
Анализ значений гиперпараметров
Если проанализировать вышеприведённые графики, то можно заметить некоторые интересные вещи, говорящие о том, как, в среднем, каждое значение гиперпараметра влияет на модель.
- n_estimators : значения 300, 500, 700, видимо, показывают наилучшие средние результаты.
- min_samples_split : маленькие значения, вроде 2 и 7, как кажется, показывают наилучшие результаты. Хорошо выглядит и значение 23. Можно исследовать несколько значений этого гиперпараметра, превышающих 2, а также — несколько значений около 23.
- min_samples_leaf : возникает такое ощущение, что маленькие значения этого гиперпараметра дают более высокие результаты. А это значит, что мы можем испытать значения между 2 и 7.
- max_features : вариант sqrt даёт самый высокий средний результат.
- max_depth : тут чёткой зависимости между значением гиперпараметра и результатом работы модели не видно, но есть ощущение, что значения 2, 3, 7, 11, 15 выглядят неплохо.
- bootstrap : значение False показывает наилучший средний результат.
Случайный лес (Random Forest)

Понятно, что такая схема построения соответствует главному принципу ансамблирования (построению алгоритма машинного обучения на базе нескольких, в данном случае решающих деревьев): базовые алгоритмы должны быть хорошими и разнообразными (поэтому каждое дерево строится на своей обучающей выборке и при выборе расщеплений есть элемент случайности).
В библиотеке scikit-learn есть такая реализация RF (привожу только для задачи классификации):
С алгоритмом работают по стандартной схеме, принятой в scikit-learn:
Опишем, что означают основные параметры:
Чем больше деревьев, тем лучше качество, но время настройки и работы RF также пропорционально увеличиваются. Обратите внимание, что часто при увеличении n_estimators качество на обучающей выборке повышается (может даже доходить до 100%), а качество на тесте выходит на асимптоту (можно прикинуть, скольких деревьев Вам достаточно).












Совет
По умолчанию в sklearn-овских методах n_jobs=1, т.е. случайный лес строится на одном процессоре. Если Вы хотите существенно ускорить построение, используйте n_jobs=-1 (строить на максимально возможном числе процессоров). Для построения воспроизводимых экспериментов используйте предустановку генератора псевдослучайных чисел: random_state.
Share this:
Понравилось это:
Похожее
Как работает случайный лес?
Алгоритм состоит из четырех этапов:
- Создайте случайные выборки из заданного набора данных.
- Для каждой выборки постройте дерево решений и получите результат предсказания, используя данное дерево.
- Проведите голосование за каждый полученный прогноз.
- Выберите предсказание с наибольшим количеством голосов в качестве окончательного результата.

Поиск важных признаков
Random forest также предлагает хороший критерий отбора признаков. Scikit-learn предоставляет дополнительную переменную при использовании модели случайного леса, которая показывает относительную важность, то есть вклад каждого показателя в прогноз. Библиотека автоматически вычисляет оценку релевантности каждого признака на этапе обучения. Затем полученное значение нормализируется так, чтобы сумма всех оценок равнялась 1.
Такая оценка поможет выбрать наиболее значимые показатели и отбросить наименее важные для построения модели.
Случайный лес использует критерий Джини, также известный как среднее уменьшение неопределенности (MDI), для расчета важности каждого признака. Кроме того, критерий Джини иногда называют общим уменьшением неопределенности в узлах. Он показывает, насколько снижается точность модели, когда вы отбрасываете переменную. Чем больше уменьшение, тем значительнее отброшенный признак. Таким образом, среднее уменьшение является необходимым параметром для выбора переменной. Также с помощью данного критерия можете быть отображена общая описательная способность признаков.
Сравнение случайных лесов и деревьев решений
- Случайный лес — это набор из множества деревьев решений.
- Глубокие деревья решений могут страдать от переобучения, но случайный лес предотвращает переобучение, создавая деревья на случайных выборках.
- Деревья решений вычислительно быстрее, чем случайные леса.
- Случайный лес сложно интерпретировать, а дерево решений легко интерпретировать и преобразовать в правила.
4. Обучение базовой модели (модель №1, RF)
Сейчас создадим модель №1. В ней, напомним, применяется только алгоритм Random Forest. Она использует все признаки и настроена с использованием значений, задаваемых по умолчанию (подробности об этих настройках можно найти в документации к sklearn.ensemble.RandomForestClassifier). Сначала инициализируем модель. После этого обучим её на масштабированных данных. Точность модели можно измерить на учебных данных:
Если нам интересно узнать о том, какие признаки являются самыми важными для RF-модели в деле предсказания рака груди, мы можем визуализировать и квантифицировать показатели важности признаков, обратившись к атрибуту feature_importances_ :
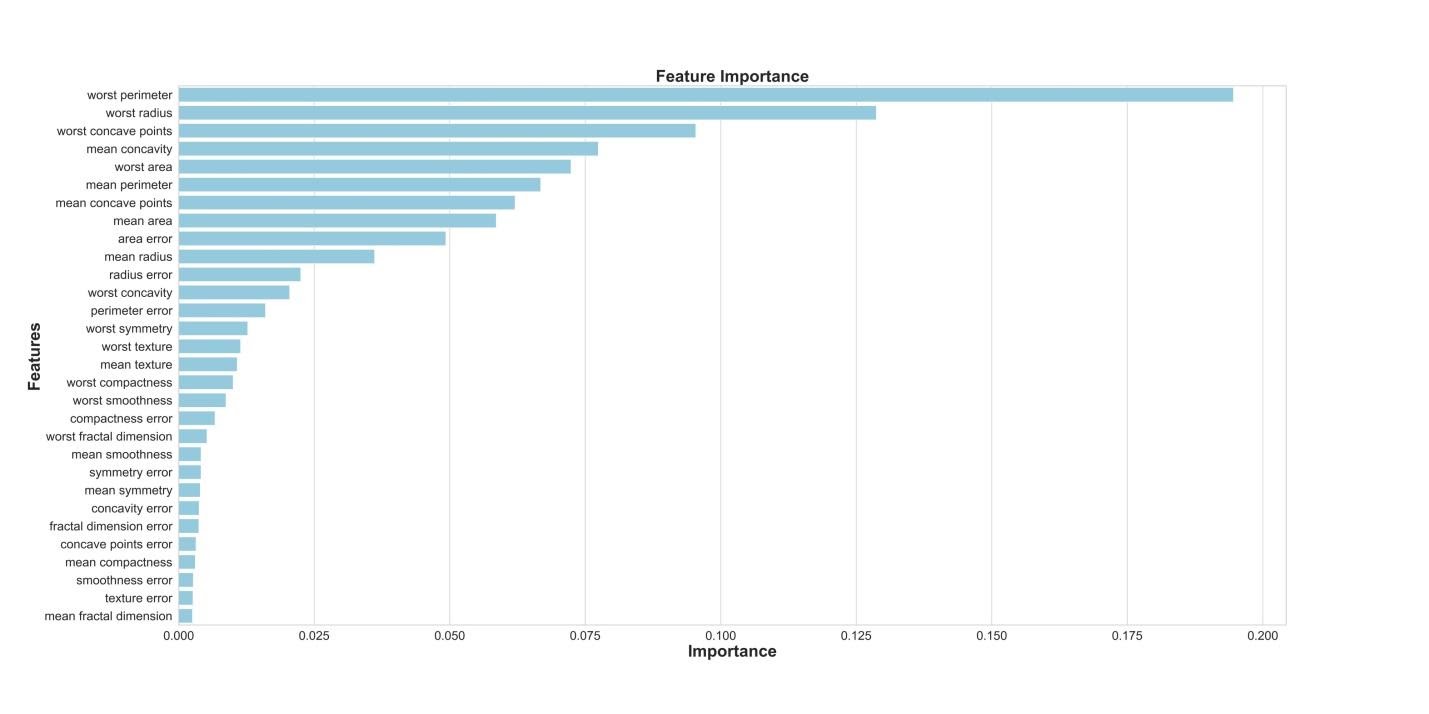
Визуализация «важности» признаков

Показатели важности признаков
Итоги
Это исследование позволяет сделать важное наблюдение. Иногда RF-модель, в которой используется метод главных компонент и широкомасштабная оптимизация гиперпараметров, может работать не так хорошо, как самая обыкновенная модель со стандартными настройками. Но это — не повод для того, чтобы ограничивать себя лишь простейшими моделями. Не попробовав разные модели, нельзя сказать о том, какая из них покажет наилучший результат. А в случае с моделями, которые используются для предсказания наличия у пациентов рака, можно сказать, что чем лучше модель — тем больше жизней может быть спасено.
2. Разделение набора данных на учебные и проверочные данные
Теперь разделим данные с использованием функции Scikit-learn train_test_split . Мы хотим дать модели как можно больше учебных данных. Однако нужно, чтобы в нашем распоряжении было бы достаточно данных для проверки модели. В целом можно сказать, что, по мере роста количества строк в наборе данных, растёт и объём данных, которые можно рассматривать в качестве учебных.
Например, если есть миллионы строк, можно разделить набор, выделив 90% строк на учебные данные и 10% — на проверочные. Но исследуемый набор данных содержит лишь 569 строк. А это — не так уж и много для тренировки и проверки модели. В результате для того, чтобы быть справедливыми по отношению к учебным и проверочным данным, мы разделим набор на две равные части — 50% — учебные данные и 50% — проверочные. Мы устанавливаем stratify=y для обеспечения того, чтобы и в учебном, и в проверочном наборах данных присутствовало бы то же соотношение 0 и 1, что и в исходном наборе данных.
Random Forest, метод главных компонент и оптимизация гиперпараметров: пример решения задачи классификации на Python
У специалистов по обработке и анализу данных есть множество средств для создания классификационных моделей. Один из самых популярных и надёжных методов разработки таких моделей заключается в использовании алгоритма «случайный лес» (Random Forest, RF). Для того чтобы попытаться улучшить показатели модели, построенной с использованием алгоритма RF, можно воспользоваться оптимизацией гиперпараметров модели (Hyperparameter Tuning, HT).

Кроме того, распространён подход, в соответствии с которым данные, перед их передачей в модель, обрабатывают с помощью метода главных компонент (Principal Component Analysis, PCA). Но стоит ли вообще этим пользоваться? Разве основная цель алгоритма RF заключается не в том, чтобы помочь аналитику интерпретировать важность признаков?
Да, применение алгоритма PCA может привести к небольшому усложнению интерпретации каждого «признака» при анализе «важности признаков» RF-модели. Однако алгоритм PCA производит уменьшение размерности пространства признаков, что может привести к уменьшению количества признаков, которые нужно обработать RF-моделью. Обратите внимание на то, что объёмность вычислений — это один из основных минусов алгоритма «случайный лес» (то есть — выполнение модели может занять немало времени). Применение алгоритма PCA может стать весьма важной частью моделирования, особенно в тех случаях, когда работают с сотнями или даже с тысячами признаков. В результате, если самое важное — это просто создать наиболее эффективную модель, и при этом можно пожертвовать точностью определения важности признаков, тогда PCA, вполне возможно, стоит попробовать.
Теперь — к делу. Мы будем работать с набором данных по раку груди — Scikit-learn «breast cancer». Мы создадим три модели и сравним их эффективность. А именно, речь идёт о следующих моделях:
- Базовая модель, основанная на алгоритме RF (будем сокращённо называть эту модель RF).
- Та же модель, что и №1, но такая, в которой применяется уменьшение размерности пространства признаков с помощью метода главных компонент (RF + PCA).
- Такая же модель, как и №2, но построенная с применением оптимизации гиперпараметров (RF + PCA + HT).
6. Обучение базовой RF-модели после применения к данным метода главных компонент (модель №2, RF + PCA)
Теперь мы можем передать в ещё одну базовую RF-модель данные X_train_scaled_pca и y_train и можем узнать о том, есть ли улучшения в точности предсказаний, выдаваемых моделью.
Модели сравним ниже.
8. Оптимизация гиперпараметров. Раунд 2: GridSearchCV (окончательная подготовка параметров для модели №3, RF + PCA + HT)
После применения алгоритма RandomizedSearchCV воспользуемся алгоритмом GridSearchCV для проведения более точного поиска наилучшей комбинации гиперпараметров. Здесь исследуются те же гиперпараметры, но теперь мы применяем более «обстоятельный» поиск их наилучшей комбинации. При использовании алгоритма GridSearchCV исследуется каждая комбинация гиперпараметров. Это требует гораздо больших вычислительных ресурсов, чем использование алгоритма RandomizedSearchCV, когда мы самостоятельно задаём число итераций поиска. Например, исследование 10 значений для каждого из 6 гиперпараметров с кросс-валидацией по 3 блокам потребует 10⁶ x 3, или 3000000 сеансов обучения модели. Именно поэтому мы и используем алгоритм GridSearchCV после того, как, применив RandomizedSearchCV, сузили диапазоны значений исследуемых параметров.
Итак, используя то, что мы выяснили с помощью RandomizedSearchCV, исследуем значения гиперпараметров, которые лучше всего себя показали:
Здесь мы применяем кросс-валидацию по 3 блокам для 540 (3 x 1 x 5 x 6 x 6 x 1) сеансов обучения модели, что даёт 1620 сеансов обучения модели. И уже теперь, после того, как мы воспользовались RandomizedSearchCV и GridSearchCV, мы можем обратиться к атрибуту best_params_ для того чтобы узнать о том, какие значения гиперпараметров позволяют модели наилучшим образом работать с исследуемым набором данных (эти значения можно видеть в нижней части предыдущего блока кода). Эти параметры используются при создании модели №3.
5. Метод главных компонент
Теперь зададимся вопросом о том, как можно улучшить базовую RF-модель. С использованием методики снижения размерности пространства признаков можно представить исходный набор данных через меньшее количество переменных и при этом снизить объём вычислительных ресурсов, необходимых для обеспечения работы модели. Используя PCA, можно изучить кумулятивную выборочную дисперсию этих признаков для того чтобы понять то, какие признаки объясняют большую часть дисперсии в данных.
Инициализируем объект PCA ( pca_test ), указывая количество компонент (признаков), которые нужно рассмотреть. Мы устанавливаем этот показатель в 30 для того чтобы увидеть объяснённую дисперсию всех сгенерированных компонент до того, как примем решение о том, сколько компонент нам понадобится. Затем передаём в pca_test масштабированные данные X_train , пользуясь методом pca_test.fit() . После этого визуализируем данные.
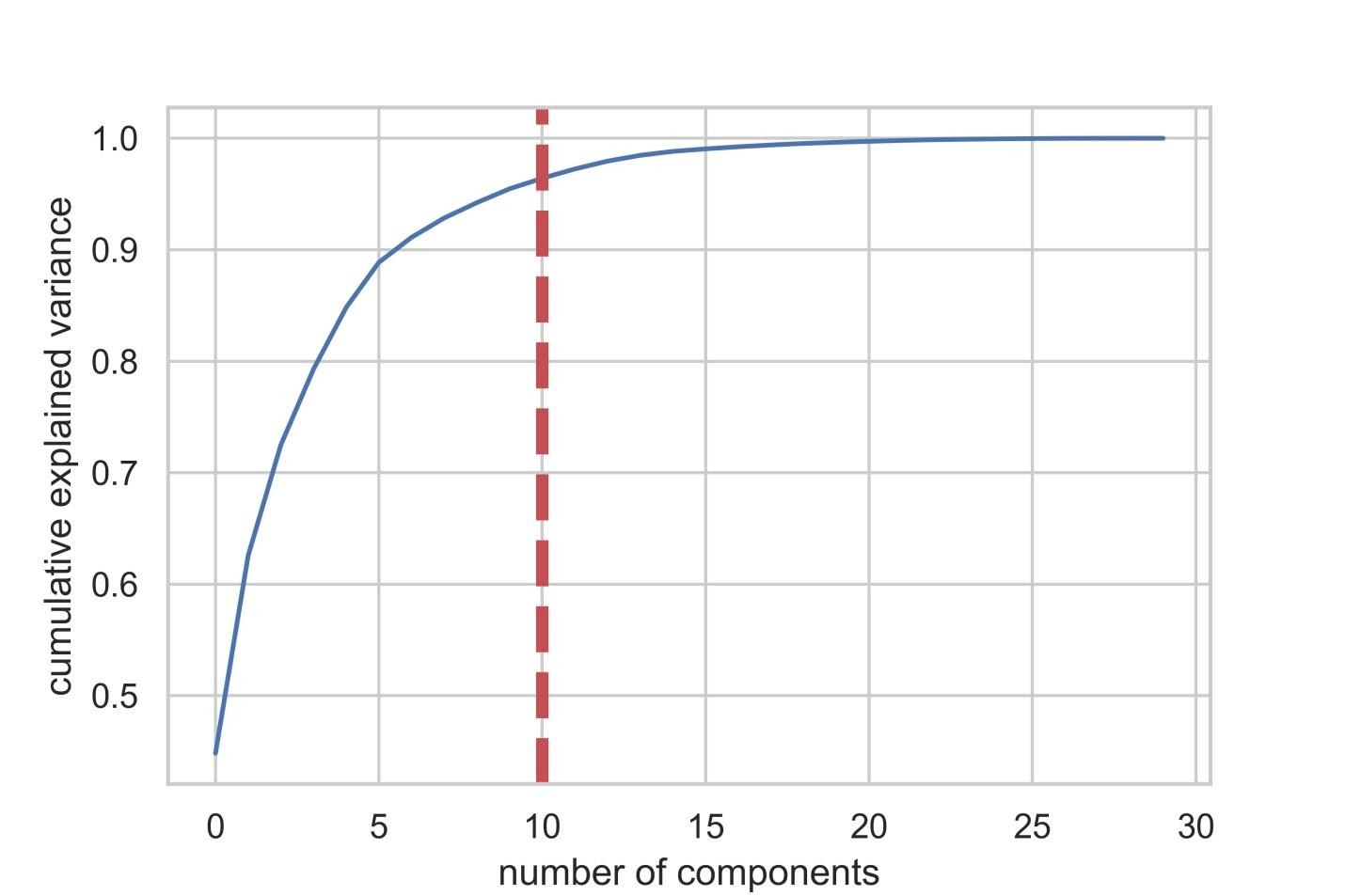
После того, как число используемых компонент превышает 10, рост их количества не очень сильно повышает объяснённую дисперсию

Этот датафрейм содержит такие показатели, как Cumulative Variance Ratio (кумулятивный размер объяснённой дисперсии данных) и Explained Variance Ratio (вклад каждой компоненты в общий объём объяснённой дисперсии)
Если взглянуть на вышеприведённый датафрейм, то окажется, что использование PCA для перехода от 30 переменных к 10 компонентам позволяет объяснить 95% дисперсии данных. Другие 20 компонент объясняют менее 5% дисперсии, а это значит, что от них мы можем отказаться. Следуя этой логике, воспользуемся PCA для уменьшения числа компонент с 30 до 10 для X_train и X_test . Запишем эти искусственно созданные наборы данных «пониженной размерности» в X_train_scaled_pca и в X_test_scaled_pca .
Каждая компонента — это линейная комбинация исходных переменных с соответствующими «весами». Мы можем видеть эти «веса» для каждой компоненты, создав датафрейм.

Датафрейм со сведениями по компонентам
Random Forest: прогулки по зимнему лесу

Это небольшое практическое руководство по применению алгоритмов машинного обучения. Разумеется, существует немалое число алгоритмов машинного обучения и способов математического (статистического) анализа информации, однако, эта заметка посвящена именно Random Forest. В заметке показаны примеры использования этого алгоритма для задач классификации и регрессии, а также даны некоторые теоретические пояснения.
2. Несколько слов о деревьях
Прежде всего, рассмотрим некоторые базовые теоретические принципы работы этого алгоритма, а начнём с такого понятия, как деревья решений. Наша основная задача — принять решение на основе имеющейся информации. В самом простом случае у нас есть всего один признак (метрика, предиктор, регрессор) с хорошо различимыми границами между классов (максимальное значение для одного класса явно меньше минимального значения для другого). Например, зная массу тела нужно отличить кита от пчелы, если известно, что среди всех наблюдений нет ни одного кита, который бы имел массу тела как у пчелы. Следовательно, достаточно всего одного показателя (предиктора), чтобы дать точный ответ, предсказав тем самым верный класс.
Допустим, что точки одного класса (пусть они будут показаны красным цветом) во всех наблюдениях находятся выше точек синего цвета. Человек может провести между ними прямую линию и сказать, что это и будет граница классов. Следовательно, всё расположенное выше этой границы будет относиться к одному классу, а всё ниже линии — к другому.

Отобразим это в виде древовидной структуры. Если мы воспользуемся одним из алгоритмов (CART) для создания дерева решений по указанным ранее данным, то получим следующее условие классификации:
Следовательно, его визуальное представление будет таким:

Разумеется, каждый признак обладает разной степенью важности. Из следующего набора данных (формат LibSVM) видно, что первый признак (его индекс 1, так как нумерация начинается не с нуля) абсолютно идентичен у представителей всех классов. Фактически, этот показатель не имеет никакой ценности для классификации, следовательно, его можно назвать избыточной информацией, которая не несёт никакой практической пользы. Аналогичная ситуация и со вторым признаком (предиктором). Однако, третий из них отличается.
Именно третий признак (feature 2) и будет служить тем самым заветным различием, с помощью которого можно предсказывать класс по вектору. Логично предположить, что задача может быть решена одним единственным условием (If-Else). Действительно, каждое дерево в алгоритме машинного обучения правильно смогло понять различия. Далее показана отладочная информация (использован классификатор Random Forest из фреймворка Apache Spark 2.1.0) для нескольких деревьев ансамбля случайного леса.
Для более сложных задач необходимы более сложные деревья. В следующем примере закономерность перестала быть такой очевидной для человека. Нужно более внимательно посмотреть набор данных, чтобы заметить различия. Условие будет немного более сложным, так как нужна дополнительная проверка.
Вот такие дополнительные проверки требуют новых ветвлений (узлов) дерева. После каждого ветвления необходимо будет делать ещё проверки, т.е. новые ветвления. Это видно на отладочной информации. В целях экономии места я привожу только несколько деревьев:
А теперь представим себе набор данных из миллиона строк и из нескольких сотен (даже тысяч) столбцов. Согласитесь, что простыми условиями такие задачи будет сложно решить. Более того, при очень сложных условиях (глубокое дерево) оно может быть слишком специфично для конкретного набора данных (переобучено). Одно дерево стойко к масштабированию данных, но не стойко к шумам. Если объединить большое количество деревьев в одну композицию, то можно получить значительно более хорошие результаты. В итоге получается весьма эффективная и достаточно универсальная модель.
3. Random Forest
Для бэггинга (независимого обучения алгоритмов классификации, где результат определяется голосованием) есть смысл использовать большое количество деревьев решений с достаточно большой глубиной. Во время классификации финальным результатом будет тот класс, за который проголосовало большинство деревьев, при условии, что одно дерево обладает одним голосом.
Так, например, если в задаче бинарной классификации была сформирована модель с 500 деревьями, среди которых 100 указывают на нулевой класс, а остальные 400 на первый класс, то в результате модель будет предсказывать именно первый класс. Если использовать Random Forest для задач регрессии, то подход выбора того решения, за которое проголосовало большинство деревьев будет неподходящим. Вместо этого происходит выбор среднего решения по всем деревьям.
Random Forest (по причине независимого построения глубоких деревьев) требует весьма много ресурсов, а ограничение на глубину повредит точности (для решения сложных задач нужно построить много глубоких деревьев). Можно заметить, что время обучения деревьев возрастает приблизительно линейно их количеству.
Естественно, увеличение высоты (глубины) деревьев не самым лучшим образом сказывается на производительности, но повышает эффективность этого алгоритма (хотя и вместе с этим повышается склонность к переобучению). Слишком сильно бояться переобучения не следует, так как это будет скомпенсировано числом деревьев. Но и увлекаться тоже не следует. Везде важны оптимально подобранные параметры (гиперпараметры).
Рассмотрим пример классификации на языке программирования R. Так как нам сейчас нужна классификационная модель, а не регрессионная, то в качестве первого параметра следует явно задать, что класс является именно фактором. Кроме количества деревьев уделим внимание числу признаков (mtry), которое будет использовать элементарная модель (дерево) для ветвлений. Фактически, это два основных параметра, которые есть смысл настраивать в первую очередь.
Убедимся, что это именно модель для классификации:
Ознакомимся с результатами confusion matrix:
Интересно увидеть предсказанные значения (на основе out-of-bag):
А функции varImpPlot и importance предназначены для отображения важности предикторов (ценности для точности работы классификатора).
Разумеется, для получения вероятного класса существует специальная функция. Она называется predict. В качестве первого аргумента требует модель, а в качестве второго — набор данных. Результатом будет вектор предсказанных классов. Для надёжной проверки необходимо выполнять тренировку на одном наборе данных, а проверку на другом наборе данных.
Ещё один пример. На этот раз используем Apache Spark 2.1.0 и язык программирования Scala. Информацию мы прочитаем из файла формата LibSVM. После этого необходимо будет явно разделить набор данных на две части. Одна из них будет учебная, а вторая — проверочная. Выполнять стандартизацию или нормализацию нет особого смысла. Наша модель устойчива к этому, равно как и достаточно устойчива к данным различной природы (вес, возраст, доход).
Повторюсь, что обучение необходимо производить только на учебной выборке. Количество классов в этом примере будет равно двум. Количество деревьев пусть будет 50. Оставим индекс Джинни в качестве критерия расщепления, так как теоретически применение энтропии не будет значительно более эффективным критерием. Глубину дерева ограничим девятью.
Теперь используем тестовый набор данных, чтобы проверить работу классификатора с указанными параметрами. Следует заметить, что порог точности (пригодность модели) определяется индивидуально в каждом конкретном случае.
Получив на вход вектор предикторов, система должна угадать (с допустимой вероятностью) класс объекта. Если в результате нескольких проверок на большом наборе данных это удалось сделать, то можно утверждать о точности модели. Однако, никакой человек и никакая система не смогут угадать с очень высокой точностью по росту человека его уровень образования. Следовательно, без правильно собранных и подготовленных данных сложно (или вообще невозможно) будет решить задачу.
4. Несколько мыслей о практическом применении
Бывают такие ситуации, когда простым условием или методами описательной статистики задачу сходу решить не получается. Как раз в задачах повышения эффективности интернет-проектов (анализ клиентов, выявление вероятности покупки, оптимальные стратегии рекламы, выбор товаров для показа в популярных блоках, рекомендации и персональные ранжирования, классификация записей в каталогах и справочниках) и встречаются подобные сложные наборы данных.
Помню, несколько лет назад впервые столкнулся с необходимостью применения ML-технологий. Была ситуация, когда мы с коллегами (группа разработчиков) пытались придумать метод классификации материалов подробного справочника на очень большом портале. Раньше классификация выполнялась вручную другими специалистами, что требовало огромного количества времени. А вот автоматизировать никак не получалось (правила и статистические методы не дали нужной точности). У нас уже был набор векторов, который ранее разметили специалисты.
Тогда меня удивило, что несколько строк кода (применение одной из популярных библиотек машинного обучения) смогли решить проблему буквально сразу. Естественно, что изучалась возможность применения различных моделей (включая нейронные сети) и продумывались рациональные гиперпараметры. Но так как эта заметка про случайный лес, то пример на языке программирования Python будет посвящён именно ему. Естественно, код примера написан с учётом новых версий готовых классификаторов, а не используемых тогда:
Таких примеров очень много. Расскажу ещё одну историю. Была задача повысить эффективность огромной системы управления рекламой. Её работа напрямую зависела от точности предсказания рейтинга товаров и услуг. У каждого из них был вектор из 64-ти признаков. Стратегически важно было заранее дать относительно точный прогноз значения рейтинга для каждого нового вектора признаков. До этого система управлялась нехитрыми правилами и описательной статистикой. Но, как известно, эффективности и точности в таких вопросах много не бывает. Для решения задачи повышения эффективности была использована регрессионная модель, похожая на указанную в примере:
В итоге мы получаем достаточно мощный инструментарий анализа информации, который способен прийти на помощь в тех задачах, где другие методы дают не самые лучшие результаты.
Случайный лес (Random Forest) : 30 комментариев
Спасибо за руководство!
Хотел бы добавить несколько наблюдений из своей практики:
«методы, основанные на деревьях, помимо задач с изображениями, не так хорошо справляются с разреженными признаками…»
Да, конечно. Хотя, в приведённых примерах главная проблема в том, что число признаков огромно, и потестить лес при достаточно большом max_features не получается. Были случаи, когда в таких задачах применялся что-то типа метода главных компонент, и потом леса работали на ура;)
«макс. глубину все равно лучше настраивать…»
У меня под рукой нет ни одного примера, где это было бы так… Вот в XGBoost это существенно, а в RF лично мне ещё ни разу не приходилось сокращать глубину, кроме описанных выше случаев.
«RF умеет оценивать важности признаков…»
Возможно, я про это отдельно напишу (тут очень много писать). На лекциях, по крайней мере, рассказываю.
«gini/entropy можно вообще не настраивать — работают практически одинаково»
Согласен. Хотя на кэгле, где борьба за сотые – надо.
«a = model.predict(X2) лучше заменить на a = model.predict_proba(X2)[:,1]»
Нет, у меня там регрессор, если заменить будет ошибка;)
«всегда ди лучше Xgboost использовать или есть примеры, когда именно RF лучше работал?»
Да, сходу не вспомню, но на том же кэгле были задачки, в которых RF был лучше. Хотя, конечно, бустинг деревьев в 95% случаев лучше усреднения.
«не получаются ли на практике OOB-оценки слишком оптимистичными»
Возможно. В sklearn-реализации я их особо не использую. Применял в самописном RF, но там я по-особому считал, получались, вроде, нормальные – не завышенные.
«Вы случайно не знаете статей, в которых теоретически обосновывалось бы использование метрик типа Джини или прироста информации?»
Нет, надо бы поискать… Как Вы сами заметили, они почти одинаково работают. Я экспериментировал, туда какую эвристику не сунь, будет примерно также! В одной из серьёзных задач оптимально было вообще разбивать выборку пополам (каждый раз выбирался признак, на котором разбиение больше всего похоже на «поровну»).
В соревновании BNP Paribas на Kaggle RF работал лучше хгбуста на стандартных признаках
3. Масштабирование данных
Прежде чем приступать к моделированию, нужно выполнить «центровку» и «стандартизацию» данных путём их масштабирования. Масштабирование выполняется из-за того, что разные величины выражены в разных единицах измерения. Эта процедура позволяет организовать «честную схватку» между признаками при определении их важности. Кроме того, мы конвертируем y_train из типа данных Pandas Series в массив NumPy для того чтобы позже модель смогла бы работать с соответствующими целевыми показателями.
Создание классификатора с использованием Scikit-learn
Вы будете строить модель на основе набора данных о цветках ириса, который является очень известным классификационным датасетом. Он включает длину и ширину чашелистика, длину и ширину лепестка, и тип цветка. Существуют три вида (класса) ирисов: Setosa, Versicolor и Virginica. Вы построите модель, определяющую тип цветка из вышеперечисленных. Этот датасет доступен в библиотеке scikit-learn или вы можете загрузить его из репозитория машинного обучения UCI.
Начнем с импорта datasets из scikit-learn и загрузим набор данных iris с помощью load_iris() .
9. Оценка качества работы моделей на проверочных данных
Теперь можно оценить созданные модели на проверочных данных. А именно, речь идёт о тех трёх моделях, описанных в самом начале материала.
Проверим эти модели:
Создадим матрицы ошибок для моделей и узнаем о том, как хорошо каждая из них способна предсказывать рак груди:

Результаты работы трёх моделей
Здесь оценивается метрика «полнота» (recall). Дело в том, что мы имеем дело с диагнозом рака. Поэтому нас чрезвычайно интересует минимизация ложноотрицательных прогнозов, выдаваемых моделями.
Учитывая это, можно сделать вывод о том, что базовая RF-модель дала наилучшие результаты. Её показатель полноты составил 94.97%. В проверочном наборе данных была запись о 179 пациентах, у которых есть рак. Модель нашла 170 из них.
Читайте также:


