Покажите как сделать сортировку слиянием снизу вверх без рекурсии
Предыдущий алгоритм можно модифицировать так, что он уже не будет использовать рекурсию. Действительно. Рассмотрим последовательно все пары элементов в сортируемом массиве. Каждый из элементов в паре представляет собой уже отсортированный массив длины 1, поэтому эти массивы (пока длины 1) можно слить в упорядоченные куски длины 2. Далее мы рассматриваем уже пары упорядоченных массивов длины 2 и сливаем их в массивы длины 4. И т.д.
Отметим, что при этих операциях на k-том проходе по упорядочиваемому массиву на правом конце массива мы будем получать либо ситуацию, когда у правого оставшегося куска (длины 2 k ) вообще нет парного куска для слияния, либо кусок есть и его длина 2 k . В первом случае делать вообще ничего не нужно, а во втором следует стандартным способом сливать куски, возможно, существенно различной длины.
Легко видеть, что данный алгоритм решает задачу за время O(N log2 N), где N – количество элементов в сортируемом массиве.
Лекция 3
Алгоритмы. Сведение алгоритмов.
Сортировки и связанные с ними задачи.
Д.Кнут. Искусство программирования для ЭВМ. тт 1-3. Москва. Мир. 1996-1998
Т.Кормен, Ч.Лейзерсон, Р.Ривест. Алгоритмы. Построение и анализ. Москва. МЦНМО. 1999.
Препарата Ф., Шеймос М. Вычислительная геометрия. Москва. Мир. 1989
Определение. Медианой множества А = a1 ,…, aN > называется элемент с индексом (N+1)/2 в отсортированном по возрастанию множестве А.
Пусть, для определенности, мы сортируем массив вещественных чисел. Идея алгоритма заключается в следующем. Выберем некоторое число, желательно близкое, в каком-то смысле, к медиане сортируемого множества. Разобьем наше множество на две половины – в одной (левой половине) должны быть элементы меньше или равные выбранного элемента, а в другой (в правой половине) – больше или равные. Из построения этих подмножеств следует, что их расположение совпадает с их расположением в отсортированном множестве чисел (расположение – в смысле множеств), т.е. после сортировки элементы из этих подмножеств останутся на месте этих же подмножеств. Т.о., применив рекурсивно эту же процедуру для каждого из подмножеств, мы, в конечном итоге, получим отсортированное множество.
Для реализации этой идеи рассмотрим алгоритм, который не предполагает хранения медианы в отдельной ячейке памяти. В процессе работы алгоритма мы будем следить за тем, в какой ячейке памяти располагается элемент исходного множества, который мы выбрали в качестве медианы. Подобная реализация в реальности чуть более медленная, но доказательство работы алгоритма намного проще, чем в случае хранения медианы в отдельной ячейке.
В следующей реализации в комментариях показаны соотношения на значения элементов, которые выполняются после каждого шага алгоритма. Эти соотношения доказывают, что каждый раз массив разбивается на части, левая из которых не превосходит медианы, а правая – не меньше медианы. Здесь для простоты множество элементов A s , A s+1 , … , A t > будем обозначать s,t>. Медиану будем обозначать M.
QuickSort(A,p,q)
Если q-p =M
поменять местами A i и A j ;//x -> Ai
//либо i==j то M== Aj => = j то
//либо i==j то p, i> = j то
//либо i==j то =x
Пока A j > x : j - -;//>=x, Aj =x
иначе
//либо i==j то Ai ==x => p,j> =x
//либо i==j+1 то p,j> =x
QuickSort(A, p, j ); QuickSort(A, j+1, q );ВЫЙТИ

Конец вечного цикла
Замечание 1. При работе алгоритм индексы массива i и j никогда не выйдут за его границы p и q.
Замечание 2. В алгоритме никогда не произойдет вечной рекурсии, т.е. при рекурсивном вызове
p j * (A,p,q)
Если q-p x и i * оказывается неверным . Это легко увидеть на простейшем примере: .
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Как мы уже видели на примере быстрой сортировки, большую часть рекурсивных алгоритмов можно усовершенствовать, обрабатывая файлы небольших размеров специальным образом. В силу рекурсивного характера функции часто вызываются именно для небольших файлов, поэтому улучшение их обработки приводит к улучшению всего алгоритма. Следовательно, как и для быстрой сортировки, переключение на сортировку вставками подфайлов небольших размеров даст улучшение времени выполнения типичной реализации сортировки слиянием на 10—15%.
Следующее полезное усовершенствование - это устранение времени копирования данных во вспомогательный массив, используемый слиянием. Для этого следует так организовать рекурсивные вызовы, что на каждом уровне процесс вычисления меняет ролями входной и вспомогательный массивы. Один из способов реализации такого подхода заключается в создании двух вариантов программ: одного для входных данных в массиве aux и выходных данных в массиве a, а другого - для входных данных в массиве a и выходных данных в массиве aux, обе эти версии поочередно вызывают одна другую. Другой подход продемонстрирован в программе 8.4, которая вначале создает копию входного массива, а затем использует программу 8.1 и переключает аргументы в рекурсивных вызовах, устраняя таким образом операцию явного копирования массива. Вместо нее программа поочередно переключается между выводом результата слияния то во вспомогательный, то во входной файл. (Это достаточно хитроумная программа.)
Программа 8.4. Сортировка слиянием без копирования
Данная рекурсивная программа сортирует массив b, помещая результат сортировки в массив a. Поэтому рекурсивные вызовы написаны так, что их результаты остаются в массиве b, а для их слияния в массив a используется программа 8.1. Таким образом, все пересылки данных выполняются во время слияний.
Данный метод позволяет избежать копирования массива ценой возвращения во внутренний цикл проверок исчерпания входных файлов. (Вспомните, что устранение этих проверок в программе 8.2 преобразовало этот файл во время копирования в бито-нический.) Положение можно восстановить с помощью рекурсивной реализации той же идеи: нужно реализовать две программы как слияния, так и сортировки слиянием: одну для вывода массива по возрастанию, а другую - для вывода массива по убыванию. Это позволяет снова использовать битоническую стратегию и устранить необходимость в сигнальных ключах во внутреннем цикле.
Поскольку при этом используются четыре копии базовых программ и закрученные рекурсивные переключения аргументов, такая супероптимизация может быть рекомендована только экспертам (ну или студентам), но все-таки она существенно ускоряет сортировку слиянием. Экспериментальные результаты, которые будут рассмотрены в разделе 8.6, показывают, что сочетание всех предложенных выше усовершенствований ускоряет сортировку слиянием процентов на 40, однако все же она процентов на 25 медленнее быстрой сортировки. Эти показатели зависят от реализации и от машины, но в разных ситуациях результаты похожи.
Другие реализации слияния, использующие явные проверки исчерпания первого файла, могут привести к более (но не очень) заметным колебаниям времени выполнения в зависимости от характера входных данных. Для случайно упорядоченных файлов после исчерпания подфайла размер другого подфайла будет небольшим, а затраты на пересылку во вспомогательный файл все так же пропорциональны размеру этого подфайла. Можно еще попытаться улучшить производительность сортировки слиянием в тех случаях, когда файл в значительной степени упорядочен, и пропускать вызов merge при полной упорядоченности файла, однако для многих типов файлов данная стратегия неэффективна.
8.16. Реализуйте абстрактное обменное слияние, использующее дополнительный объем памяти, пропорциональный размеру меньшего из сливаемых файлов. (Этот метод должен сократить наполовину потребность сортировки в памяти.)
8.17. Выполните сортировку слиянием больших случайно упорядоченных файлов и экспериментально определите среднюю длину другого подфайла на момент исчерпания первого подфайла как функцию от N (сумма длин двух сливаемых подфайлов).
8.18. Предположим, программа 8.3 модифицирована так, что не вызывает метод merge при a[m] . Сколько сравнений экономится в этом случае, если сортируемый файл уже упорядочен?
8.19. Выполните модифицированный алгоритм, предложенный в упражнении 8.18, для больших случайно упорядоченных файлов. Экспериментально определите среднее количество пропусков вызова merge в зависимости от N (размер исходного сортируемого файла).
8.20. Допустим, что сортировка слиянием должна быть выполнена на h-сортированном файле для небольшого значения h. Какие изменения нужно внести в подпрограмму merge, чтобы воспользоваться этим свойством входных данных? Поэкспериментируйте с гибридами сортировки методом Шелла и сортировки слиянием, основанными на этой подпрограмме.
8.21. Разработайте реализацию слияния, уменьшающую требование дополнительной памяти до max(M, N/M) за счет следующей идеи. Разбейте массив на N/M блоков размером M (для простоты предположим, что N кратно M). Затем, (1) рассматривая эти блоки как записи, первые ключи которых являются ключами сортировки, отсортируйте их с помощью сортировки выбором, и (2) выполните проход по массиву, сливая первый блок со вторым, затем второй блок с третьим и так далее.
8.22. Докажите, что метод, описанный в упражнении 8.21, выполняется за линейное время.
8.23. Реализуйте битоническую сортировку слиянием без копирования.
Восходящая сортировка слиянием
Как было сказано в "Рекурсия и деревья" , у каждой рекурсивной программы имеется нерекурсивный аналог, который хотя и выполняет эквивалентные действия, но может делать это в другом порядке. Нерекурсивные реализации сортировки слиянием заслуживают детального изучения в качестве образцов философии алгоритмов " разделяй и властвуй " .
Рассмотрим последовательность слияний, выполняемую рекурсивным алгоритмом. Из примера, приведенного на рис. 8.2, видно, что файл размером 15 сортируется следующей последовательностью слияний:
Порядок выполнения слияний определяется рекурсивной структурой алгоритма. Но подфайлы обрабатываются независимо, поэтому слияния могут выполняться в различном порядке. На рис. 8.4 показана восходящая стратегия, при которой последовательность слияний такова:

Последовательность слияний, выполняемая рекурсивным алгоритмом, определяется деревом " разделяй и властвуй " , показанным на рис. 8.3: мы просто выполняем обратный проход по этому дереву. Как было показано в "Элементарные структуры данных" , можно разработать нерекурсивный алгоритм, использующий явный стек, который даст ту же последовательность слияний. Однако совсем не обязательно ограничиваться только обратным порядком: любой проход по дереву, при котором обход поддеревьев узла завершается перед посещением самого узла, дает правильный алгоритм. Единственное ограничение заключается в том, что сливаемые файлы должны быть предварительно отсортированы. В случае сортировки слиянием удобно сначала выполнять все слияния 1-и-1 , затем все слияния 2-и-2 , затем все 4-и-4 , и так далее. Такая последовательность соответствует обходу дерева по уровням, который поднимается по дереву снизу вверх.
В "Рекурсия и деревья" мы уже видели на нескольких приме -рах, что при рассуждении в стиле снизу-вверх имеет смысл переориентировать мышление в сторону стратегии " объединяй и властвуй " , когда сначала решаются небольшие подзадачи, а затем они объединяются для получения решения большей задачи. В частности, нерекурсивный вариант вида " объединяй и властвуй " сортировки слиянием в программе 8.5 получается следующим образом: вначале все элементы файла рассматриваются как упорядоченные подсписки длиной 1. Потом для них выполняются слияния 1-и-1 , и получаются упорядоченные подсписки размером 2, затем выполняется серия слияний 2-и-2 , что дает упорядоченные подсписки размером 4, и так далее до упорядочения всего списка. Если размер файла не является степенью 2, то последний подсписок не всегда имеет тот же размер, что и все другие, но его все равно можно слить.
Если размер файла является степенью 2, то множество слияний, выполняемых восходящей сортировкой слиянием, в точности совпадает с множеством слияний, выполняемым рекурсивной сортировкой слиянием, однако последовательность слияний будет другой. Восходящая сортировка слиянием соответствует обходу дерева " разделяй и властвуй " по уровням, снизу вверх. В противоположность этому, рекурсивный алгоритм называется нисходящей сортировкой слиянием - в силу обратного обхода дерева сверху вниз.
Если размер файла не равен степени 2, восходящий алгоритм дает другое множество слияний, как показано на рис. 8.5. Восходящий алгоритм соответствует дереву " объединяй и властвуй " (см. упражнение 5.75), отличному от дерева " разделяй и властвуй " , которое соответствует нисходящему алгоритму. Можно сделать так, чтобы последовательность слияний, выполняемых рекурсивным методом, была такой же, как и для нерекурсивного метода, однако для этого нет особых причин, поскольку разница в производительности невелика по отношению к общим затратам.
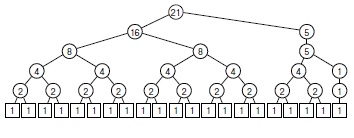
Если размер файла не равен степени 2, то структуры слияний для восходящей сортировки слиянием совершенно не похожи на структуры слияний для нисходящей сортировки ( рис. 8.3). При восходящей сортировке размеры всех файлов (возможно, за исключением последнего) равны степени 2. Эти различия помогают понять базовую структуру алгоритмов, но почти не влияют на производительность.
Леммы 8.1-8.4 справедливы и для восходящей сортировки слиянием, при этом имеют место следующие дополнительные леммы:
Лемма 8.5. Все слияния на каждом проходе восходящей сортировки слиянием манипулируют файлами, размер которых равен степени 2, за исключением, возможно, размера последнего файла.

Это факт легко доказать методом индукции.
Лемма 8.6. Количество проходов при восходящей сортировке слиянием по файлу из N элементов в точности равно числу битов в двоичном представлении N (без ведущих нулей). Размер подсписков после к проходов равен 2 k , т.к. на каждом проходе восходящей сортировки слиянием размер упорядоченных подфайлов удваивается. Значит, количество проходов, необходимое для сортировки файла из N элементов, есть наименьшее к такое, что , что в точности равно \rceil$" />
, т.е. количеству битов в двоичном представлении N. Этот результат можно доказать и методом индукции или с помощью анализа структурных свойств деревьев " объединяй и властвуй " . ¦
Программа 8.5. Восходящая сортировка слиянием
Восходящая сортировка слиянием состоит из последовательности проходов по всему файлу с выполнением слияний вида m-и-m и с удвоением m на каждом проходе. Последний подфайл имеет размер m лишь тогда, когда размер файла является четным кратным m, так что последнее слияние имеет тип m-и-х , для некоторого х, меньшего или равного m.

Для упорядочения файла из 200 элементов восходящая сортировка слиянием выполняет лишь семь проходов по файлу. Каждый проход вдвое уменьшает количество упорядоченных подфайлов и удваивает их длину (кроме, возможно, последнего).
Процесс выполнения восходящей сортировки слиянием большого файла показан на рис. 8.6. Сортировка 1 миллиона элементов выполняется за 20 проходов по данным, 1 миллиарда - за 30 проходов и т.д.
Подводя итоги, отметим, что нисходящая и восходящая сортировки - это два простых алгоритма сортировки, основанных на операции слияния двух упорядоченных подфайлов в результирующий объединенный упорядоченный файл. Оба алгоритма тесно связаны между собой и даже выполняют одно и то же множество слияний, если размер исходного файла является степенью 2, но они отнюдь не идентичны. На рис. 8.7 демонстрируются различия динамических характеристик алгоритмов на примере большого файла. Каждый алгоритм может использоваться на практике, если экономия памяти не важна, и желательно гарантированное время выполнения в худшем случае. Оба алгоритма представляют интерес как прототипы общих принципов построения алгоритмов: " разделяй и властвуй " и " объединяй и властвуй " .

Восходящая сортировка слиянием (слева) выполняет серию проходов по файлу, которые сливают упорядоченные подфайлы, пока не останется только один. Каждый элемент файла, за исключением, возможно, последнего, участвует в каждом проходе. В отличие от этого, нисходящая сортировка слиянием (справа) вначале упорядочивает первую половину файла, а затем берется за вторую половину (рекурсивно), поэтому диаграмма ее работы существенно отличается.
8.24. Покажите, какие слияния выполняет восходящая сортировка слиянием (программа 8.5) для ключей E A S Y Q U E S T I O N .
8.25. Реализуйте восходящую сортировку слиянием, которая начинает с сортировки вставками блоков по M элементов. Определите эмпирическим путем значение M, для которого разработанная программа быстрее всего сортирует произвольно упорядоченные файлы из N элементов, при N = 10 3 , 10 4 , 10 5 и 10 6 .
8.26. Нарисуйте деревья, которые отображают слияния, выполняемые программой 8.5 для N = 16, 24, 31, 32, 33 и 39 .
8.27. Напишите программу рекурсивной сортировки слиянием, выполняющую те же слияния, что и восходящая сортировка слиянием.
8.28. Напишите программу восходящей сортировки слиянием, выполняющую те же слияния, что и нисходящая сортировка слиянием. (Это упражнение намного труднее, чем упражнение 8.27).
8.29. Предположим, что размер файла является степенью 2. Удалите рекурсию из нисходящей сортировки слиянием так, чтобы получить нерекурсивную сортировку слиянием, выполняющую ту же последовательность слияний.
8.30. Докажите, что количество проходов, выполняемых нисходящей сортировкой слиянием, также равно количеству битов в двоичном представлении числа N (см. лемму 8.6).
Разделяем массив на части, пока он не будет равен 1 элементу. Каждый 1 элемент является отсортированным.
Слияние отсортированных элементов.
По принципу двух колод карт. Кладем 2 колоды карт на стол вверх значениями, и карту которая из них младше, кладем в третью результирующую стопку карт. В конечном итоге, если карты в какой-то колоде закончились, перекладываем их по очереди в результирующую. Получится слитый из двух отсортированных массивов, один, новый, отсортированный массив.
не работает. возьмем два массива <1,3,4>и на третьем прогоне PositionB сравняется с длинной массива, и начнет добавлять только из первого массива,тогда как во втором еще осталась 5ка.
Он делит данный список на две половины, вызывает себя для двух половин, а затем объединяет две отсортированные половины. Мы определяем функцию merge(), используемую для объединения двух половинок.
Подсписки снова и снова делятся на половины, пока мы не получим по одному элементу в каждом. Затем мы объединяем пару списков из одного элемента в два списка элементов, сортируя их в процессе. Две отсортированные пары элементов объединяются в четыре списка и так далее, пока мы не получим отсортированный список.
Концепция сортировки слиянием
Давайте посмотрим на следующий пример сортировки слиянием.
Мы разделили данный список на две половины. Список нельзя разделить на равные части, это не имеет значения.
Сортировку слиянием можно реализовать двумя способами: сверху вниз и снизу вверх. В приведенном примере мы используем подход сверху вниз, который чаще всего используется с сортировкой слиянием.
Подход снизу вверх обеспечивает большую оптимизацию, которую мы определим позже.
Основная часть алгоритма заключается в том, как мы объединяем два отсортированных подсписка. Давайте объединим два отсортированных списка слиянием.
- A: [2, 4, 7, 8]
- B: [1, 3, 11]
- Сортировано: пусто
Сначала мы наблюдаем первый элемент обоих списков. Мы обнаружили, что первый элемент B меньше, поэтому мы добавляем его в наш отсортированный список и продвигаемся вперед в списке B.
- A: [2, 4, 7, 8]
- B: [1, 3, 11]
- Сортировано: 1
Теперь мы посмотрим на следующую пару элементов 2 и 3. 2 меньше, поэтому мы добавляем ее в наш отсортированный список и переходим к списку.
- A: [2, 4, 7, 8]
- B: [1, 3, 11]
- Сортировано: 1
Продолжите этот процесс, и мы получим отсортированный список из .
Могут быть два особых случая:
- Что делать, если в обоих подсписках есть одинаковые элементы – в этом случае мы можем переместить любой подсписок и добавить элемент в отсортированный список. Технически мы можем двигаться вперед по обоим подспискам и добавлять элементы в отсортированный список.
- У нас не осталось ни одного элемента в одном подсписке. Когда мы заканчиваем в подсписке, просто добавляем элемент второго один за другим.
Следует помнить, что отсортировать элемент можно в любом порядке. Мы сортируем данный список в порядке возрастания, но мы можем легко отсортировать его в порядке убывания.
Реализация
Сортировочный массив
Основная концепция алгоритма – разделить (под) список на половины и рекурсивно отсортировать их. Мы продолжаем процесс до тех пор, пока не получим списки, содержащие только один элемент. Давайте разберемся со следующей функцией деления:
Наша основная задача – разделить список на части до того, как произойдет сортировка. Нам нужно получить целочисленное значение, поэтому мы используем оператор // для наших индексов.
Разберем описанную выше процедуру, выполнив следующие шаги:
- Первый шаг – создать копии списков. Первый список содержит списки из [left_index, …, middle], а второй из [middle + 1. Right_index].
- Мы просматриваем обе копии с помощью указателя, выбираем меньшее из двух значений и добавляем их в отсортированный список. Как только мы добавляем элемент, мы продвигаемся вперед по отсортированному списку.
- Добавим оставшиеся элементы из другой копии в отсортированный массив.
Реализуем сортировку слиянием на примере.
Сортировка настраиваемых объектов
Мы также можем отсортировать настраиваемые объекты с помощью класса Python. Этот алгоритм почти аналогичен приведенному выше, но нам нужно сделать его более универсальным и передать функцию сравнения.
Мы создадим собственный класс Car и добавим в него несколько полей. Мы внесем несколько изменений в приведенный ниже алгоритм, чтобы сделать его более универсальным. Мы можем сделать это с помощью лямбда-функций.
Оптимизация
Мы можем улучшить производительность алгоритма сортировки слиянием. Сначала давайте поймем разницу между сортировкой слияния сверху вниз и снизу вверх. Подход снизу вверх сортирует элементы смежных списков итеративно, а подход сверху вниз разбивает списки на две половины.
Данный список [10, 4, 2, 12, 1, 3], вместо того, чтобы разбивать его на [10], [4], [2], [12], [1], [3] – мы делим в подсписки, которые уже могут быть отсортированы: [10, 4], [2], [1, 12], [3] и теперь готовы их отсортировать.
Сортировка слиянием – неэффективный алгоритм как во времени, так и в пространстве для меньших подсписков. Таким образом, сортировка вставкой является более эффективным алгоритмом, чем сортировка слиянием для меньших подсписков.
Заключение
Сортировка слиянием – популярный и эффективный алгоритм. Он более эффективен для больших списков и не зависит от каких-либо неудачных решений, которые приводят к задержке выполнения.
Но есть один серьезный недостаток. Она использует дополнительную память, которая используется для хранения временных копий списков перед их объединением. Она работает быстро и дает отличный результат.
Мы кратко обсудили концепцию сортировки слиянием и реализовали ее как для простого целочисленного списка, так и для пользовательских объектов с помощью лямбда-функции, используемой для сравнения.
Сортировка слиянием (англ. Merge sort) — алгоритм сортировки, использующий [math]O(n)[/math] дополнительной памяти и работающий за [math]O(n\log(n))[/math] времени.
Содержание



- Если в рассматриваемом массиве один элемент, то он уже отсортирован — алгоритм завершает работу.
- Иначе массив разбивается на две части, которые сортируются рекурсивно.
- После сортировки двух частей массива к ним применяется процедура слияния, которая по двум отсортированным частям получает исходный отсортированный массив.
У нас есть два массива [math]a[/math] и [math]b[/math] (фактически это будут две части одного массива, но для удобства будем писать, что у нас просто два массива). Нам надо получить массив [math]c[/math] размером [math]|a| + |b|[/math] . Для этого можно применить процедуру слияния. Эта процедура заключается в том, что мы сравниваем элементы массивов (начиная с начала) и меньший из них записываем в финальный. И затем, в массиве у которого оказался меньший элемент, переходим к следующему элементу и сравниваем теперь его. В конце, если один из массивов закончился, мы просто дописываем в финальный другой массив. После мы наш финальный массив записываем заместо двух исходных и получаем отсортированный участок.
Множество отсортированных списков с операцией [math]\mathrm[/math] является моноидом, где нейтральным элементом будет пустой список.
Ниже приведён псевдокод процедуры слияния, который сливает две части массива [math]a[/math] — [math][left; mid)[/math] и [math][mid; right)[/math]
Функция сортирует подотрезок массива с индексами в полуинтервале [math][left; right)[/math] .
При итеративном алгоритме используется на [math]O(\log n)[/math] меньше памяти, которая раньше тратилась на рекурсивные вызовы.
Чтобы оценить время работы этого алгоритма, составим рекуррентное соотношение. Пускай [math]T(n)[/math] — время сортировки массива длины [math]n[/math] , тогда для сортировки слиянием справедливо [math]T(n)=2T(n/2)+O(n)[/math]
[math]O(n)[/math] — время, необходимое на то, чтобы слить два массива длины [math]n[/math] . Распишем это соотношение:
Читайте также:


