Модель тригонометрического круга своими руками
“Знания, приобретенные путем простого зубрения, почти неизбежно забываются совершенно бесследно. Наоборот, умственный материал, набираемый памятью постепенно, день за днем, в связи с различными контекстами, связанный ассоциативно с другими внешними событиями и неоднократно подвергший обсуждению, образует такую систему, вступает в такую связь с остальными сторонами нашего интеллекта, легко возобновляется в памяти массою внешних поводов, что остается надолго прочным приобретением”.
С тех пор прошло более 100 лет, а слова эти поразительно остаются злободневными. В этом каждодневно убеждаешься, занимаясь со школьниками. Массовые пробелы в знаниях настолько велики, что можно утверждать: школьный курс математики в дидактическом и психологическом отношениях – не система, а некое устройство, поощряющее кратковременную память и нисколько не заботиться о памяти долговременной.
Знать школьный курс математики – значит владеть материалом каждого из направлений математики, быть в состоянии актуализировать любое из них в любое время. Чтобы достичь этого, нужно систематически обращаться каждому из них, что порой не всегда возможно из-за сильной загруженности на уроке.
Есть другой путь долговременного запоминания фактов и формул – это опорные сигналы.
Тригонометрия – один из больших разделов школьной математики, изучаемой в курсе геометрии 8, 9 классов и в курсе алгебры 9 класса, алгебры и начал анализа в 10 классе.
Самый большой объем изучаемого материала по тригонометрии приходится на долю 10 класса. Большую часть этого материала из тригонометрии можно изучить и запомнить на тригонометрическом круге (окружность единичного радиуса с центром в начале прямоугольной системы координат). Приложение1.ppt
- определения синуса, косинуса, тангенса и котангенса угла;
- радианное измерение углов;
- область определения и область значений тригонометрических функций
- значения тригонометрических функций для некоторых значений числового и углового аргумента;
- периодичность тригонометрических функций;
- четность и нечетность тригонометрических функций;
- возрастание и убывание тригонометрических функций;
- формулы приведения;
- значения обратных тригонометрических функций;
- решение простейших тригонометрических уравнений;
- решение простейших неравенств;
- основные формулы тригонометрии.
Рассмотрим изучение этих понятий на тригонометрическом круге.
1) Определение синуса, косинуса, тангенса и котангенса.
После введения понятия тригонометрического круга (окружность единичного радиуса с центром в начале координат), начального радиуса (радиус окружности по направлению оси Ох), угла поворота, учащиеся самостоятельно получают определения для синуса, косинуса, тангенса и котангенса на тригонометрическом круге, используя определения из курса геометрии, то есть, рассматривая прямоугольный треугольник с гипотенузой, равной 1.
Косинусом угла называется абсцисса точки на окружности при повороте начального радиуса на данный угол.
Синусом угла называется ордината точки на окружности при повороте начального радиуса на данный угол.
2) Радианное измерение углов на тригонометрическом круге.
После введения радианной меры угла (1 радиан – это центральный угол, которому соответствует длина дуги, равная длине радиуса окружности), учащиеся делают вывод, что радианное измерение угла – это числовое значение угла поворота на окружности, равное длине соответствующей дуги при повороте начального радиуса на заданный угол. .
Тригонометрический круг разделен на 12 равных частей диаметрами окружности. Зная, что угол радианам, можно определить радианное измерение для углов кратных .
А радианные измерения углов, кратных, получаются аналогично:
3) Область определения и область значений тригонометрических функций.
Будет ли соответствие углов поворота и значений координат точки на окружности функцией?
Каждому углу поворота соответствует единственная точка на окружности, значит данное соответствие – функция.
На тригонометрическом круге видно, что область определения функций – множество всех действительных чисел, а область значений - .
Введем понятия линий тангенсов и котангенсов на тригонометрическом круге.
1) Пусть Введем вспомогательную прямую, параллельную оси Оу, на которой определяются тангенсы для любого числового аргумента.
2) Аналогично получаем линию котангенсов. Пусть у=1, тогда . Значит, значения котангенса определяются на прямой, параллельной оси Ох.
На тригонометрическом круге без труда можно определить область определения и область значений тригонометрических функций:
4) Значения тригонометрических функций на тригонометрическом круге.
Катет , противолежащий углу в равен половине гипотенузы, то есть Другой катет по теореме Пифагора:
Значит по определению синуса, косинуса, тангенса, котангенса можно определить значения для углов кратных или радианам. Значения синуса определяются по оси Оу, косинуса по оси Ох, а значения тангенса и котангенса можно определить по дополнительным осям, параллельным осям Оу и Ох соответственно.
Табличные значения синуса и косинуса расположены на соответствующих осях следующим образом:
Табличные значения тангенса и котангенса -
5) Периодичность тригонометрических функций.
На тригонометрическом круге видно, что значения синуса, косинуса повторяются через каждые радиана, а тангенса и котангенса – через радиан.
6)Четность и нечетность тригонометрических функций.
Это свойство можно получить, сравнивая значения положительных и им противоположных углов поворота тригонометрических функций. Получаем, что
Значит, косинус – четная функция, все остальные функции – нечетные.
7) Возрастание и убывание тригонометрических функций.
По тригонометрическому кругу видно, что функция синус возрастает и убывает
Аналогично рассуждая, получаем промежутки возрастания и убывания функций косинуса, тангенса и котангенса.
8) Формулы приведения.
За угол берем меньшее значение угла на тригонометрическом круге. Все формулы получаются в сравнении значений тригонометрических функций на катетах выделенных прямоугольных треугольников.
Алгоритм применения формул приведения:
1) Определить знак функции при повороте на заданный угол.
При повороте на угол функция сохраняется, при повороте на угол - целое, нечетное число, получается кофункция (
9) Значения обратных тригонометрических функций.
Введем обратные функции для тригонометрических функций, пользуясь определением функции.
Каждому значению синуса, косинуса, тангенса и котангенса на тригонометрическом круге соответствует только одно значение угла поворота. Значит, для функции область определения , область значений - Для функции область определения - , область значений - . Аналогично получаем область определения и область значений обратных функций для косинуса и котангенса.
Алгоритм нахождения значений обратных тригонометрических функций:
1) нахождение на соответствующей оси значения аргумента обратной тригонометрической функции;
2) нахождение угла поворота начального радиуса с учетом области значений обратной тригонометрической функции.
10) Решение простейших уравнений на тригонометрическом круге.
Чтобы решить уравнение вида , найдем точки на окружности, ординаты которых равны и запишем соответствующие углы с учетом периода функции.
Для уравнения , найдем точки на окружности, абсциссы которых равны и запишем соответствующие углы с учетом периода функции.
Аналогично для уравнений вида Значения определяются на линиях тангенсов и котангенсов и записываются соответствующие углы поворота.
11) Решение неравенств.
Чтобы решить неравенства вида , необходимо найти точки на окружности с ординатой и прочитать соответствующее неравенство против часовой стрелки с учетом периода функции.
Чтобы решить неравенства вида , необходимо найти точки на окружности с абсциссой и прочитать соответствующее неравенство против часовой стрелки с учетом периода функции.
Чтобы решить неравенства вида , необходимо найти точку на линии тангенсов с координатой и прочитать соответствующее неравенство против часовой стрелки с учетом области определения и периода функции.
Аналогично для неравенств с котангенсом.
Необходимо практиковать чтение промежутков на тригонометрическом круге, тогда решения неравенств определяются безошибочно.
12) Основные формулы тригонометрии.
1) Основные тригонометрические тождества.
Очевидны выводы формул которые получаются в прямоугольном треугольнике на тригонометрическом круге.
2) Формулы сложения выводятся с использованием скалярного произведения векторов начального и “конечного” радиусов.
Другие формулы сложения получаются с использованием предыдущей, формул приведения и свойств четности и нечетности тригонометрических функций.
Почти все формулы тригонометрии являются следствиями этих основных формул.
Все понятия и формулы тригонометрии получают сами ученики под четким руководством учителя с помощью тригонометрического круга. В дальнейшем этот “круг” будет служить для них опорным сигналом или внешним фактором для воспроизведения в памяти понятий и формул тригонометрии.
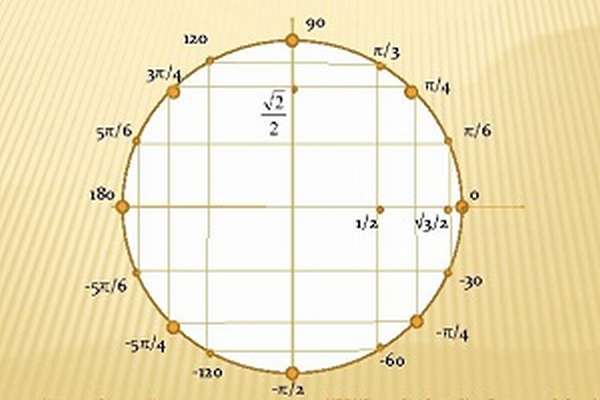
Тригонометрический круг один из основных элементов геометрии для решения уравнений с синусом, косинусом, тангенсом и котангенсом.
Каково определение данного термина, как строить данный круг, как определить четверть в тригонометрии, как узнать углы в построенном тригонометрическом круге — об этом и многом другом расскажем далее.
Тригонометрическая окружность
Тригонометрическим видом числовой окружности в математике является круг, имеющий одинарный радиус с центром в начале координатной плоскости. Как правило, она образована пространством из формул синуса с косинусом, тангенсом и котангенсом на системе координат.
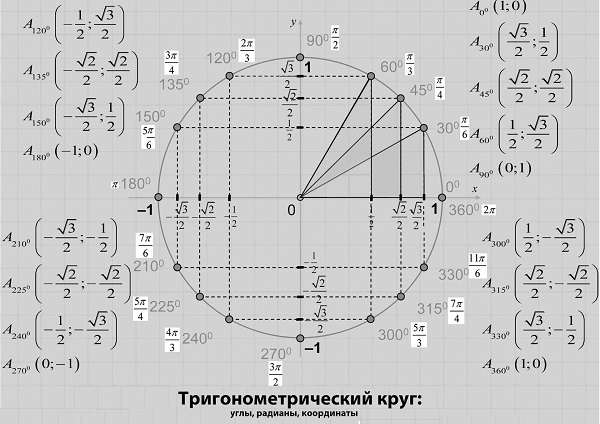
Назначение такой сферы с n-мерным пространством в том, что благодаря ей могут быть описаны тригонометрические функции. Выглядит она просто: круг, внутри которого находится система координат и множественные прямоугольного вида треугольники, образованные из этой окружности по тригонометрическим функциям.
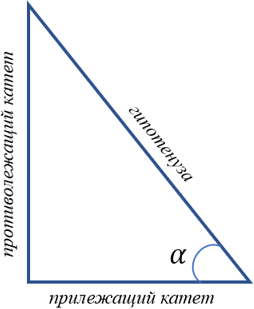
Что такое синус, косинус, тангенс, котангенс в прямоугольном треугольнике
Прямоугольный вид треугольника — это тот, у которого один из углов равен 90°. Он образован катетами и гипотенузой со всеми значениями тригонометрии. Катеты две стороны треугольника, которые прилегают к углу 90°, а третья гипотенуза, она всегда длиннее катетов.
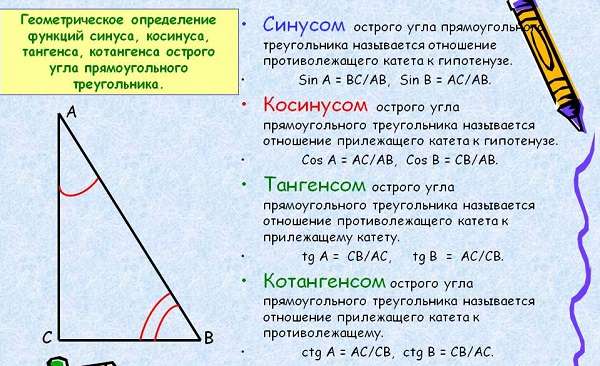
Синусом называется отношение одного из катетов к гипотенузе, косинусом отношение другого катета к ней, а тангенсом отношение двух катетов. Отношение символизирует деление. Также тангенсом является деление острого угла на синус с косинусом. Котангенсом является противоположное тангенсу отношение.
Формулы последних двух отношений выглядят следующим образом: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a).
Построение единичной окружности
Построение единичной окружности сводится к ее прорисовке с единичным радиусом в центре системы координат. Затем для построения нужно отсчитать углы и, двигаясь против часовой стрелки, обойти по целому кругу, проставляя соответствующие им линии координаты.
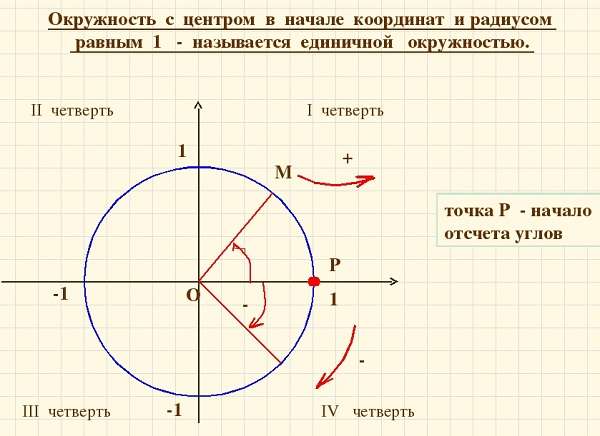
Начинается построение после черчения круга и установки точки в его центре с размещения системы координат ОХ. Точкой О сверху оси координат является синус, а Х косинус. Соответственно они являются абсциссой и ординатой. Затем нужно провести измерения ∠. Они проводятся градусами и радианами.
Сделать перевод этих показателей просто полный круг равен двум пи радиан. Угол от нуля против часовой стрелки идет со знаком +, а ∠ от 0 по часовой стрелке со знаком -. Положительные и отрицательные значения синуса с косинусом повторяются каждый оборот круга.
Углы на тригонометрическом круге
Для того, чтобы освоить теорию тригонометрической окружности, нужно понять, как считаются ∠ на ней, и в чем они измеряются. Считаются они очень просто.
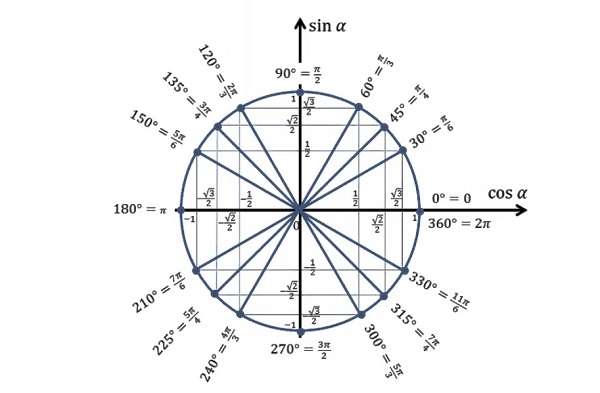
Окружность делится системой координат на четыре части. Каждая часть образует ∠ 90°. Половина от этих углов равняется 45 градусам. Соответственно две доли окружности равняются 180°, а три 360°. Как пользоваться этой информацией?
Если требуется решить задачу по нахождению ∠, прибегают к теоремам о треугольниках и основным Пифагоровым законам, связанных с ними.
Измеряются углы в радианах:
- от 0 до 90° значения углов от 0 до ∏/2,
- от 90 до 180° значения углов от ∏/2 до ∏,
- от 180 до 270° от ∏ до 3*∏/2,
- последняя четверть от 2700 до 3600 — значения от 3*∏/2 до 2*∏.
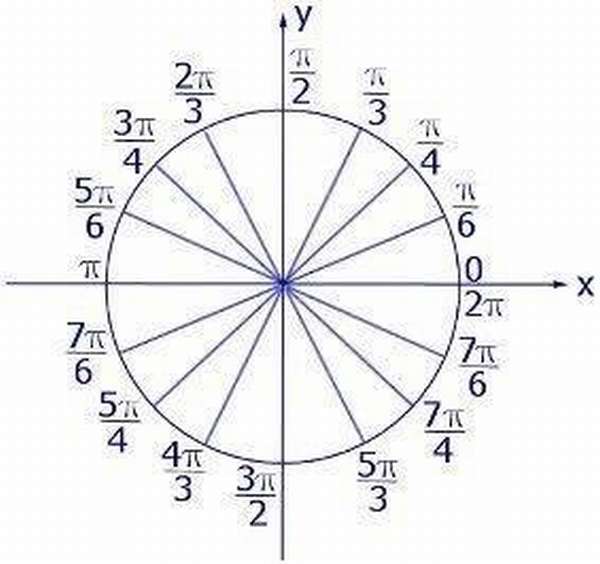
Чтобы узнать конкретное измерение, перевести радианы в градусы или наоборот, следует прибегнуть к таблице-шпаргалке.
Перевод углов из градусов в радианы
Углы возможно измерить в градусах либо радианах. Требуется осознавать связь между обоими значениями. Эта взаимосвязь выражена в тригонометрии с помощью специальной формулы. Благодаря пониманию связи, можно научиться оперативным образом управлять углами и переходить от градусов к радианам обратно.
Для того чтобы точно узнать, чему равен один радиан, можно воспользоваться следующей формулой:
1 рад. = 180 / ∏ = 180 / 3,1416 = 57,2956
В конечном итоге, 1 радиан равен 57°, а в 1 градусе 0,0175 радиан:
1 градус = (∏ /180) рад. = 3,1416 / 180 рад. = 0,0175 рад.

Косинус, синус, тангенс, котангенс на тригонометрической окружности
Косинус с синусом, тангенсом и котангенсом на тригонометрической окружности функции углов альфа от 0 до 360 градусов. Каждая функция обладает положительным или отрицательным значением в зависимости от того, какая величина у угла. Они символизируют отношения к прямоугольным треугольникам, образованным в круге.
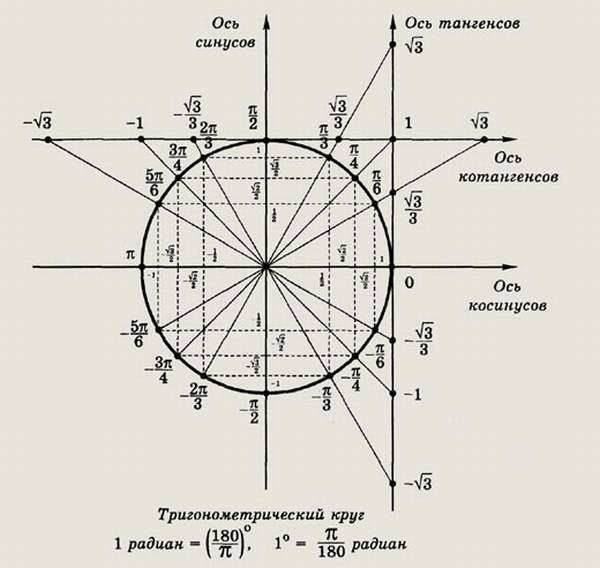

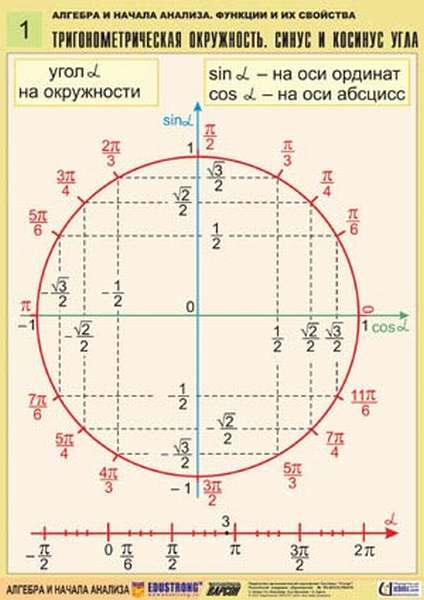

Заключение
В целом, тригонометрическая окружность – единичная окружность, необходимая для решения соответствующих задач и описания функций. Она состоит из многих составляющих, запомнить которые нужно обязательно для правильного решения последующих задач.
Тригонометрия пришла людям на помощь, когда выяснилось, что для многих расчетов недостаточно тех углов, которые определялись обычной геометрией. И правда, в геометрии мы не встретим углы больше, чем 360⁰. Ненасытные ученые хотели больше. Поэтому, по сути, тригонометрия – это раздел математики, посвященный углам.
Нарисуем тригонометрический круг.
Алгоритм для создания тригонометрического круга:
- Рисуем системы координат;
- Изображаем круг. Центр совпадает с центром системы координат. Рекомендуется выбирать за длину радиуса 4, 6 или 8 клеточек в зависимости от того, какого размера вы хотите круг.
- Ставим точку отсчёта 0 для измерения углов.
- Затем изобразим угол: одну сторону зафиксируем на горизонтальной оси, а другая останется свободной и сможет крутиться, куда вздумает, как на шарнире.
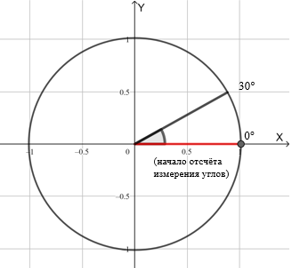
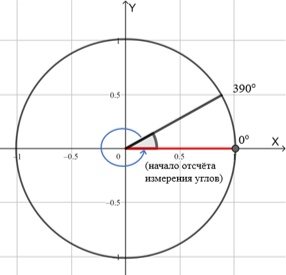
- Теперь мысленно вращаем незакрепленную сторону. Пусть она вращается против часовой стрелки. Вот она совершила полный оборот и вернулась на свое место. Визуально угол остался прежним, но на самом деле к нему добавился полный оборот, то есть 360⁰.
- Учитывая полные обороты, каждый угол можно представить, как
$ a+360^ \cdot n $, где n – целое число
Договоримся, что вращение против часовой стрелки – это положительно направление, а по часовой – отрицательное.
Измерение углов
В математике углы измеряют не только в привычных нам градусах, но и в радианах. Соответствие между ними установить очень просто.
Некоторые углы очень легко определить:
Можно пользоваться формулой: $ \alpha = \frac <\phi\cdot\pi> $
Также есть обратная формула: $ \phi = \frac <(\alpha \cdot 180)> <\pi>$
| Градусы | Радианы |
| $ 0^$ | 0 |
| $ 30^$ | $ \frac <\pi>$ |
| $ 45^$ | $\frac <\pi>$ |
| $ 60^$ | $\frac <\pi>$ |
| $ 90^$ | $\frac <\pi>$ |
| $ 180^$ | $ \pi $ |
| $ 360^$ | $ 2\pi $ |
Изображение табличных значений на тригонометрическом круге.
Нарисуем тригонометрический круг.
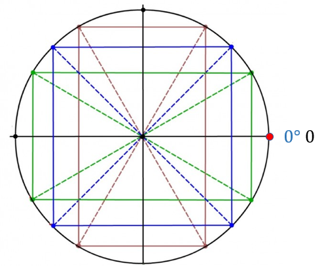
Далее идём по кругу с шагом в 45, то есть, $ \frac <\pi> $. Эти углы делят каждую четверть пополам.
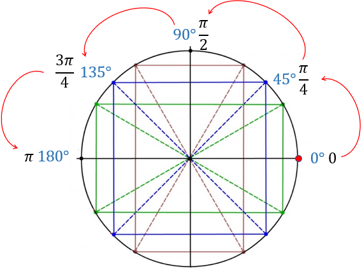
Затем идём по кругу с шагом в 30, то есть, $ \frac <\pi> $, Каждая четверть таким образом делится на 3 равные части.
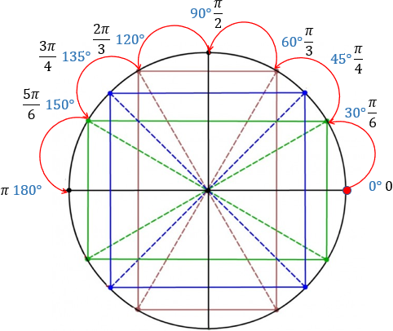
Снизу заполним не большими углами, а отрицательными. То есть, зеркально отразим верхнюю часть круга вниз.
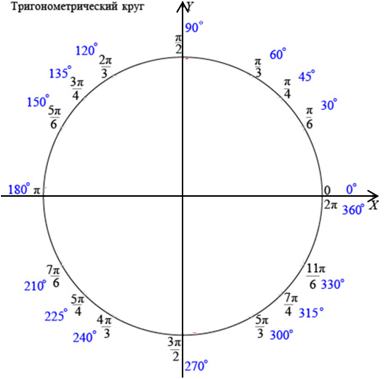
Теперь заполним новый круг, но уже углами от 0 до $ 2\pi $.
Определение значений тригонометрических функций
| $ sin \; \alpha = \frac $ | $ cos \; \alpha = \frac $ |
| $ tg \; \alpha = \frac $ | $ ctg \; \alpha = \frac $ |
Снова перейдем к окружности. Вставим в нее прямоугольный треугольник так, чтобы гипотенуза совпала с радиусом, который мы будем принимать за 1.
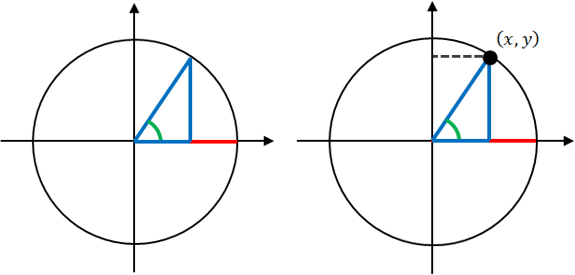
Точка пересечения радиуса с окружностью, как и любая точка в плоскости, имеют свои координаты (x,y). Причем, для отмеченного нами угла противолежащий катет равен y, а прилежащий – x. А теперь немного магии. Заменим на x, y и 1 величины в определении тригонометрических функций.
| $ sin \; \alpha = \frac =y $ | $ cos \; \alpha = \frac =x $ |
| $ tg \; \alpha = \frac =\frac $ | $ ctg \; \alpha = \frac =\frac $ |
Получается, что косинус – это значения на оси абсцисс, а синус – значения на оси ординат.
Ось тангенсов параллельна оси синусов и проходит через точку с координатой x = 1, ось котангенсов параллельна оси косинусов и проходит через точку y = 1. Соответствующее значение на них получается продлением радиуса до пересечения с одной из осей.

Единичная окружность — идеальный инструмент для тригонометрических операций. В этой статье узнаем больше про этот вид окружности и возможных с ней действиях.
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.

Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
- Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
- Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
- В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
- В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:

Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
- 2π радиан = 360°
- 1 радиан = (360/2π) градусов
- 1 радиан = (180/π) градусов
- 360° = 2π радиан
- 1° = (2π/360) радиан
- 1° = (π/180) радиан
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.
Уравнение единичной окружности
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:


Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Читайте также:


