Метод стьюдента как сделать в экселе
Функция СТЮДРАСПОБР предназначена для расчета значения квантиля уровня, соответствующего известной вероятности (указывается в качестве первого аргумента), распределения Стьюдента для известных степеней свободы и возвращает обратное t-распределение.
Распределение Стьюдента и нормальное распределение в Excel
Рассматриваемая функция возвращает значение t, соответствующее условию P(|x|>t)=p. Здесь x является значением некоторой случайной величины с распределением Стьюдента, у которого число степеней свобод соответствует k (второй аргумент функции СТЮДРАСПОБР).
- Распределение Стьюдента является одним из видов распределения случайной величины, близкое к нормальному распределению с характерным отличием – сниженная концентрацией отклонений в средней части распределения. Иное название – t-распределение.
- Квантилем считается некоторое значение, которое с определенной вероятностью (фиксированной) не будет превышено случайной величиной.
- Функция СТЮДРАСПОБР считается устаревшей начиная с версии MS Office 2010. Она оставлена для обеспечения совместимости с другими табличными редакторами и документами, созданными в более старых версиях табличного редактора. В новых версиях следует использовать усовершенствованные аналоги: СТЬЮДЕНТ.ОБР.2Х или СТЬЮДЕНТ.ОБР.
Ниже рассмотрим примеры использования функции СТЮДРАСПОБР в Excel.
Определение одностороннего и двустороннего t распределение Стьюдента
Пример 1. Определить односторонне и двустороннее t-значения для распределения Стьюдента, характеризующееся вероятностью 0,17 и числом степени свобод 16.
Вид таблицы данных:

Для расчета двустороннего t-значения используем функцию:

Для двустороннего t используем удвоенное значение вероятности:
В результате получим:

Число степеней свободы в распределении Стьюдента
Пример 2. Сгенерировать 8 случайных чисел с использованием функции СЛЧИС, для которых распределение Стьюдента имеет 4 степени свободы.
Поскольку вероятность того, что случайна величина примет как отрицательное, так и положительное значение является одинаковой и равна 0,5 (распределение Стьюдента симметрично относительно вертикальной оси графика), используем функцию ЕСЛИ для проверки значений.
Выделим 8 ячеек и запишем следующую функцию (вводить как формулу массива CTRL+SHIFT+Enter):
То есть, если случайное значение вероятности, сгенерированное функцией СЛЧИС меньше 0,5, будет сгенерировано отрицательное t-значение, иначе – положительное.

Небольшая памятка для студентов и аналитиков всех отраслей: как использовать Microsoft Excel для вычисления критерия Стьюдента.

Microsoft Excel имеет мощные инструменты для анализа и визуализации статистики. В этой статье мы продемонстрируем их на примере классической статистической процедуры: теста Стьюдента или t-теста.
t-тест: что это такое, и зачем это нужно?
Тест Стьюдента позволяет сравнивать случайные выборки данных — либо с некой нормой, либо между собой. Например, завод выпускает шурупы, и нужно оценить, соответствуют ли они в норме по длине. Или в больнице ведется клиническое исследование лекарства, и нужно оценить его эффект на пациентах до и после приема.
В обоих случаях должно выполняться требование нормальности распределения исследуемого признака в каждой из сравниваемых групп. Результатом выполнения теста является число, отражающее данный показатель — t-критерий, или критерий Стьюдента.
t-тест: как выполнить в MS Excel?
Вне зависимости от того, для чего вам может понадобиться вычислить критерий Стьюдента, в Microsoft Excel есть функция TTEST, которая позволяет это сделать. Она доступна в надстройке Пакет анализа. Рассмотрим, как использовать функцию на примере Microsoft Excel 2013 в Windows 7.
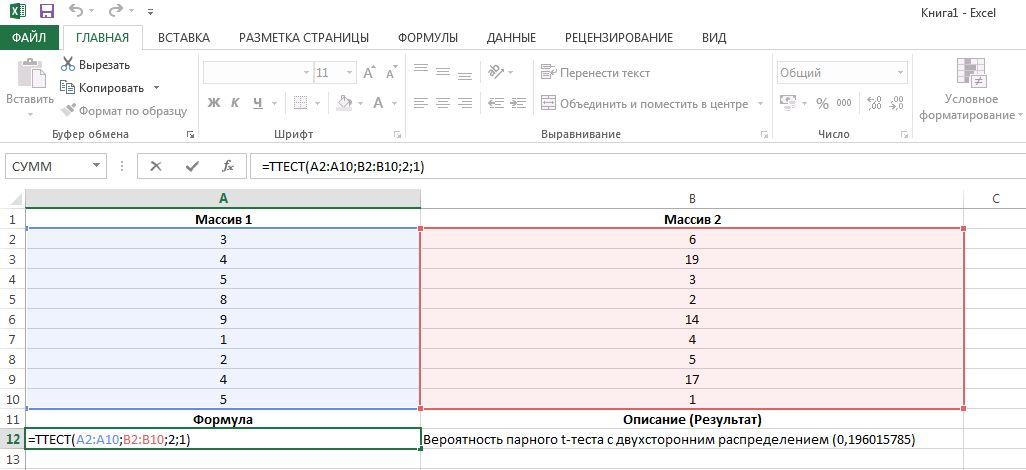
Как выполнить t-тест в Excel 2013
Синтаксис функции следующий: ТТЕСТ(массив1;массив2;хвосты;тип). Скопируйте эту формулу в любое поле вашего документа Excel.
– общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.

Уильям Госсет
Расчет показателя в Excel
Теперь перейдем непосредственно к вопросу, как рассчитать данный показатель в Экселе. Его можно произвести через функцию СТЬЮДЕНТ.ТЕСТ. В версиях Excel 2007 года и ранее она называлась ТТЕСТ. Впрочем, она была оставлена и в позднейших версиях в целях совместимости, но в них все-таки рекомендуется использовать более современную — СТЬЮДЕНТ.ТЕСТ. Данную функцию можно использовать тремя способами, о которых подробно пойдет речь ниже.
Мастер функций
Проще всего производить вычисления данного показателя через Мастер функций.
-
Строим таблицу с двумя рядами переменных.


- 1 – выборка состоит из зависимых величин;
- 2 – выборка состоит из независимых величин;
- 3 – выборка состоит из независимых величин с неравным отклонением.

Выполняется расчет, а результат выводится на экран в заранее выделенную ячейку.


Условия применения t-критерия Стьюдента
Несмотря на то, что открытие Стьюдента в свое время совершило переворот в статистике, t-критерий все же довольно сильно ограничен в возможностях применения, т.к. сам по себе происходит из предположения о нормальном распределении исходных данных. Если данные не являются нормальными (что обычно и бывает), то и t-критерий уже не будет иметь распределения Стьюдента. Однако в силу действия центральной предельной теоремы средняя даже у ненормальных данных быстро приобретает колоколообразную форму распределения.
Рассмотрим, для примера, данные, имеющие выраженный скос вправо, как у распределения хи-квадрат с 5-ю степенями свободы.

Теперь создадим 20 тысяч выборок и будет наблюдать, как меняется распределение средних в зависимости от их объема.
Отличие довольно заметно в малых выборках до 15-20-ти наблюдений. Но дальше оно стремительно исчезает. Таким образом, ненормальность распределения – это, конечно, нехорошо, но некритично.

Картина получается нерадостная. Фактические частоты средних сильно отличаются от теоретических. Использование t-распределения в такой ситуации становится весьма рискованной затеей.
Итак, в не очень малых выборках (от 15-ти наблюдений) t-критерий относительно устойчив к ненормальному распределению исходных данных. А вот выбросы в данных сильно искажают распределение t-критерия, что, в свою очередь, может привести к ошибкам статистического вывода, поэтому от аномальных наблюдений следует избавиться. Часто из выборки удаляют все значения, выходящие за пределы ±2 стандартных отклонения от средней.
Для того, чтобы рассчитать t-критерий Стьюдента (для зависимых и для независимых выборок) в Excell необходимо сделать следующие шаги:
1.Вносим значения для двух переменных в таблицу (Например Переменная 1 и Переменная 2)
2. Ставим курсор в пустую ячейку
3. На панеле инструментов нажимаем кнопку fx (вставить формулу)
5.1. Нажимаем Ок
Критерий Стьюдента в Microsoft Excel

Одним из наиболее известных статистических инструментов является критерий Стьюдента. Он используется для измерения статистической значимости различных парных величин. Microsoft Excel обладает специальной функцией для расчета данного показателя. Давайте узнаем, как рассчитать критерий Стьюдента в Экселе.
Определение термина
Но, для начала давайте все-таки выясним, что представляет собой критерий Стьюдента в общем. Данный показатель применяется для проверки равенства средних значений двух выборок. То есть, он определяет достоверность различий между двумя группами данных. При этом, для определения этого критерия используется целый набор методов. Показатель можно рассчитывать с учетом одностороннего или двухстороннего распределения.
Расчет показателя в Excel
Теперь перейдем непосредственно к вопросу, как рассчитать данный показатель в Экселе. Его можно произвести через функцию СТЬЮДЕНТ.ТЕСТ. В версиях Excel 2007 года и ранее она называлась ТТЕСТ. Впрочем, она была оставлена и в позднейших версиях в целях совместимости, но в них все-таки рекомендуется использовать более современную — СТЬЮДЕНТ.ТЕСТ. Данную функцию можно использовать тремя способами, о которых подробно пойдет речь ниже.
Способ 1: Мастер функций
Проще всего производить вычисления данного показателя через Мастер функций.



- 1 – выборка состоит из зависимых величин;
- 2 – выборка состоит из независимых величин;
- 3 – выборка состоит из независимых величин с неравным отклонением.

Выполняется расчет, а результат выводится на экран в заранее выделенную ячейку.




Способ 3: ручной ввод
Формулу СТЬЮДЕНТ.ТЕСТ также можно ввести вручную в любую ячейку на листе или в строку функций. Её синтаксический вид выглядит следующим образом:
Что означает каждый из аргументов, было рассмотрено при разборе первого способа. Эти значения и следует подставлять в данную функцию.

После того, как данные введены, жмем кнопку Enter для вывода результата на экран.

Как видим, вычисляется критерий Стьюдента в Excel очень просто и быстро. Главное, пользователь, который проводит вычисления, должен понимать, что он собой представляет и какие вводимые данные за что отвечают. Непосредственный расчет программа выполняет сама.
Мы рады, что смогли помочь Вам в решении проблемы.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Читайте также:


