Курносый додекаэдр как сделать
Подразделы: Новые звездчатые формы, Модели многогранников из бумаги, Звёздчатые формы и соединения тел, Выпуклые многогранники, Архимедовы тела, Правильные звездчатые многогранники (тела Кеплера-Пуансо), Полуправильные звездчатые многогранники
Здесь находятся обзорные изображения многогранников, важных для теории или просто очень красивых. Чтобы увидеть интерактивную 3d модель многогранника в полном качестве и управлять параметрами отображения и раскраски, нажмите на понравившееся изображение. Имеются также фото многогранников из бумаги, сделанных вашими руками. Искать новые прекрасные звездчатые многогранники можно найти на странице звездчатые формы.
Некоторые важные звёздчатые формы и соединения тел
Изменение вида завершающих звездчатых форм в ряду из 12 многогранников с №56 по №43 по мере удаления икосаэдральной плоскости от центра тела
Другие звёздчатые многогранники можно найти на странице звездчатых форм.
Лучшие звездчатые формы, найденные пользователями сайта
Если Вам удалось найти особенно красивый или интересный многогранник, то его можно разместить здесь.
| Завершающая звездчатая форма усеченного тетраэдра. Похожа на Кеплеровскую stella octangula, только тетраэдры разного размера, и симметрия лишь тетраэдральная | Завершающая звездчатая форма ромбоикосододекаэдра. Появление ромбической грани привело к резкому увеличению изрезанности пиков | Одна из звездчатых форм курносого додекаэдра. Просто поражает своею сложностью! | Псевдо вариант квазиусеченного кубоктаэдра. Эта тело не упоминается в книге Веннинджера "Модели многогранников", хотя он и русская редакция много пишут о псевдоварианте квазикубоктаэдра. Возможно тело №41' не известно науке и здесь представлено впервые! |
|---|
Фотографии моделей многогранников из бумаги, изготовленные вашими руками
Если вы изготовили своими руками сложный многогранник, то фотографию или видео можно разместить здесь.
Фото соединения пяти тетраэдров от Коли (правый и левый варианты)  | Фото ромбоикосододекаэдра от Коли  |
| Фотографии различных звездчатых форм кубооктаэдра и икосододекаэдра из обширной коллекции Александра Скуснова | |
 |  |
Платоновы тела (выпуклые правильные многогранники)
Пять платоновых тел были гордостью Пифагорейской школы.
| Тетраэдр, №1 | Октаэдр, №2 | Куб, №3 | Икосаэдр, №4 | Додекаэдр, №5 |
Архимедовы тела (выпуклые полуправильные многогранники)
| Усеченный тетраэдр, №6 | Усеченный октаэдр, №7 | Усеченный куб, №8 | Усеченный икосаэдр, №9 | Усеченный додекаэдр, №10 |
| Кубооктаэдр, №11 | Икосододекаэдр, №12 | Ромбокубоктаэдр, №13 | Ромбоикосододекаэдр, №14 |
| Ромбоусеченный кубооктаэдр, №15 | Ромбоусеченный икосододекаэдр, №16 | Курносый куб, №17 | Курносый додекаэдр, №18 |
Тела Кеплера-Пуансо (звездчатые правильные многогранники)
| Звездчатые додекаэдры могут быть получены как звездчатые формы додекаэдра 1№5, 2№5, 3№5 | Большой икосаэдр, №22 (звездоформа икосаэдра 2№4) | ||
| Малый звездчатый додекаэдр, №19 | Большой додекаэдр, №20 | Большой звездчатый додекаэдр, №21 | |
Полуправильные звездчатые многогранники (однородные многогранники)
| Тетрагемигексаэдр, №23 | Октагемиоктаэдр, №24 | Кубогемиоктаэдр, №34 | Малый икосогемидодекаэдр, №45 | Малый додекогемидодекаэдр, №47 |
| Большой кубокубооктаэдр, №33 | Большой ромбогексаэдр, №59 | Малый кубокубоктаэдр, №25 | Малый ромбогексаэдр, №42 | Квазиромбокубоктаэдр, №41 |
| Малый додекоикосододекаэдр, №28 | Малый ромбододекаэдр, №30 | Усеченный большой додекаэдр, №31 | Додекододекаэдр, №29 | Малый додекогемиикосаэдр, №56 |
| Большой додекогемиикосаэдр, №58 | Усеченный большой икосаэдр, №51 | Малый битригональный икосододекаэдр, №26 | Битригональный додекаэдр, №36 | Большой битригональный икосододекаэдр, №43 |
| Малый икосоикосододекаэдр, №27 | Малый битригональный додекоикосододекаэдр (открыт в 1954 году), №38 | Малый додекоикосаэдр (открыт в 1954 году), №46 | Ромбододекододекаэдр, №32 | Икосододекододекаэдр, №39 |
| Ромбоикосаэдр, №52 | Кубоусеченный кубооктаэдр, №35 | Икосододекоусеченный икосододекаэдр, №40 | Квазиусеченный кубооктаэдр, №49 | Квазиусеченный додекаэдр, №54 |
| Большой битригональный додекоикосододекаэдр, №37 | Большой додекоикосаэдр, №57 | Большой икосоикосододекаэдр, №44 | Квазиусеченный гексаэдр, №48 | Большой икосододекаэдр, №50 |
| Большой икосогемидодекаэдр, №62 | Большой додекогемидодекаэдр, №63 | Квазиусеченный звездчатый додекаэдр, №53 | Квазиусеченный большой звездчатый додекаэдр, №60 | Большой додекоикосододекаэдр, №55 |
| Квазиромбоикосододекаэдр, №61 | Большой ромбододекаэдр, №65 | Большой квазиусеченный икосододекаэдр, №64 | Малый курносый икосододекаэдр, №66 | Курносый додекододекаэдр, №67 |
| Курносый икосододекододекаэдр, №68 | Большой вывернутый курносый икосододекаэдр, №69 | Вывернутый курносый додекододекаэдр, №70 | Большой курносый додекоикосододекаэдр, №71 | Большой курносый икосододекаэдр, №72 |
| Большой вывернутый обратнокурносый икосододекаэдр, №73 | Малый вывернутый обратнокурносый икосоикосододекаэдр, №74 | Большой биромбоикосододекаэдр, №75 |
Неурожай из года в год То льют дожди, то слишком сухо Не даром говорит народ: "Ну, не понос — так золотуха".
В основе додекаэдра лежит 12 пятиугольных граней, которые образуют 20 вершин и 30 ребер. Перед нами — платоново тело, то есть симметричная фигура из одинаковых деталей. Собственно, бумажный додедаэдр изготавливают и склеивая распечатанный/вырезанный шаблон. Но есть другой — простой, интересный способ.
Как сделать из бумаги додекаэдр: пошагово

додекаэдр шаблон пронумерованный
Бумагу желательно брать достаточно плотную. А главное, поверхность должна быть не гладкой, чтобы сила трения до закрепления клеем удерживала клапаны в кармашках.
Курносый додекаэдр
Курносый додекаэдр принадлежит к семейству архимедовых тел, то есть полуправильных выпуклых многогранников. Этот многограник относится к додекаэдру так же, как курносый куб относится к кубу. Его пятиугольные грани лежат в плоскостях граней описанного додекаэдра, но слегка повернуты по отношению к ним. В зависимости от направления поворота можно указать правую и левую модификации этого многогранника, отличающиеся так же, как правая и левая руки - каждая из этих модификаций получается из другой отражением в зеркале.
Можно сделать все пятиугольники одного цвета - например, желтого. Треугольники, примыкающие к пятиугольникам, можно все окрасить в один цвет - это удовлетворяет принципу раскраски карт - но более эффектно, если каждая пятерка треугольников имеет свой собственный цвет, соответствующий четырехцветной окраске описанного додекаэдра. В этом случае дополнительные связывающие треугольники можно окрасить в тот же цвет, что и пятиугольники.
Для изготовления модели окружите каждый пятиугольник пятью треугольниками. Вы получите двенадцать заготовок. Соедините их, используя дополнительные треугольники.
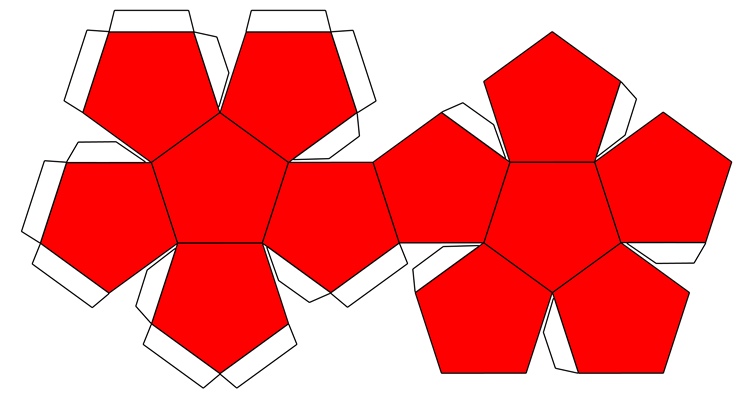
Додекаэдр (двенадцатигранник) - правильный многогранник, составленный из двенадцати правильных пятиугольников.

Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра).
Додекаэдр похож на футбольный мяч, ещё такая же фигура получается при сборке новогодних шаров из цветного картона. В Википедии можно прочитать о вычислении объёма додекаэдра.
Читайте также:


