Когда sin меняется на cos
Применять формулы приведения - легко! Их не надо зубрить наизусть. И не надо тащить на экзамен шпаргалки, рискуя спалиться. Надо всего лишь запомнить два правила, о которых вы узнаете, посмотрев этот ролик. Это так просто, что даже лошадка поймет! :-) Посмотри и передай друзьям.
Часто в задачах встречаются выражения вида а также или — то есть такие, где к аргументу прибавляется нечетное число, умноженное на или целое число, умноженное на Они упрощаются с помощью формул приведения.
Запомните: формулы приведения, от слова «привести». К привидениям, то есть к призракам и прочим глюкам, эти формулы отношения не имеют : -)
Эти формулы называются так потому, что с их помощью можно привести выражения к более простым.
Например,
Зубрить наизусть формулы приведения не нужно. Достаточно знать правило, состоящее из двух пунктов.
1) Если в тригонометрической формуле к аргументу прибавляется (или вычитается из него) — в общем, угол, лежащий на вертикальной оси, — функция меняется на кофункцию. Синус меняется на косинус, косинус на синус, тангенс на котангенс и наоборот.
Если же мы прибавляем или вычитаем — в общем, то, что лежит на горизонтальной оси, — функция на кофункцию не меняется.
Это легко запомнить. Если прибавляемый угол лежит на вертикальной оси — вертикально киваем головой, говорим: «Да, да, меняется функция на кофункцию». Если прибавляемый угол лежит на горизонтальной оси — горизонтально мотаем головой, говорим: «Нет, нет, не меняется функция на кофункцию».
Это первая часть правила. Теперь вторая.
2) Знак получившегося выражения такой же, каким будет знак тригонометрической функции в левой его части, при условии, что аргумент мы берем из первой четверти.
Упростим, например, выражение Функция меняется на кофункцию — и в результате получится синус. Взяв x из первой четверти и прибавив к нему попадем во вторую четверть. Во второй четверти косинус отрицателен. Значит, получится

Посмотрим, как формулы приведения применяются в задачах ЕГЭ по математике.
Примеры из ЕГЭ с формулами приведения:
Пример. (Задание из ЕГЭ) Найдите значение выражения \(\frac^°> >^°>>\)
Углы \(^°\) и \(^°\) нестандартные, поэтому «в лоб» без калькулятора вычислить непросто. Однако использовав формулы привидения, мы легко найдем правильный ответ.
Прежде всего, обратите внимание на один важный момент: \(49^°=90^°-41^°\). Поэтому мы можем заменить \(49^°\) на \(90^°-41^°\).
Теперь применим к синусу формулу приведения:
\(90^°-41^°\) – это первая четверть, синус в ней положителен. Значит, знак будет плюс;
\(90^°\)- находится на «вертикали» - функция меняется на кофункцию.
В числителе и знаменателе получились одинаковые косинусы. Сокращаем их.
Пример. (Задание из ЕГЭ) Найдите значение выражения \(\frac\)
Опять замечаем интересное «совпадение»: \(163^°=180^°-17^°\). Поэтому можно заменить \(163^°\) на \(180^°-17^°\).
Воспользуемся формулой приведения:
\((180^°-17^°)\) – это вторая четверть, тангенс в ней отрицателен. Значит, знак будет минус;
\(180^°\) - находится на «горизонтали» - функция остается прежней.
Пример. (Задание из ЕГЭ) Найдите значение выражения \(-19\,tg\,101^°\cdot tg\,191^°\)
Применим формулы приведения:
\((90^°+11^°)\) – это вторая четверть, тангенс в ней отрицателен. Значит, знак будет минус;
\(90^°\)- находится на «вертикали» - функция меняется.
\((180^°+11^°)\) – это третья четверть, тангенс в ней положителен. Значит, знак будет плюс;
\(180^°\) - находится на «горизонтали» - функция остается прежней.
Вот тут можно применить одну из формул связи .
Пример. (Задание из ЕГЭ) Вычислить: \(\frac^° + sin^2^°>\) .
\((90^°+41^°)\) – \(90^°\) на вертикали, синус меняется на косинус;
Знак синуса не важен, так как он все равно в квадрате.
\((180^°+41^°)\) – \(180^°\) на горизонтальной оси, синус остается синусом.
Пример. (Задание из ЕГЭ) Найдите \(26\, cos(\frac+α)\), если \(cosα=\frac\) и \(α∈(\frac;2π)\).
Очевидно, что к исходному выражению можно применить формулу приведения \(26\,cos(\frac+α)=26\,sinα\). Задача свелась к нахождению синуса по косинусу, много похожих заданий было разобрано в статье « формулы связи ».
С учетом того, что \(α∈(\frac;2π)\), то есть в четвертой четверти, \(sin\,α=-\frac\).
Ну и последний пример – с очень важным выводом после него.
Пример. (Задание из ЕГЭ) Вычислить, чему равен \(ctg(-a-\frac)\), если \(tg\,a=2\).
Прежде чем применять формулу приведения, приведем аргумент функции к стандартному (одному из указанных в начале статьи). Давайте поменяем местами слагаемые аргумента, сохраняя знаки – для того, чтобы a стояла после «точки привязки».
Уже лучше, но все еще есть проблемы – «точка привязки» с минусом, а такого аргумента у нас нет. Избавимся от минуса, вынеся его за скобку внутри аргумента.
Теперь вспомним о том, что котангенс – функция нечетная, то есть \(ctg\,(-t)=- ctg\,t\). Преобразовываем наше выражение.
Теперь преобразуем \(\frac\) следующим образом: \(\frac=\frac=2π+\frac\).
Но ведь \(2π\) – это просто полный оборот по кругу, он не оказывает никакого влияния на значение функции: \(ctg\,(2π+x)=ctg(x)\).
Так что, его можно просто отбросить.
Вот теперь применяем формулу приведения.
\((\frac+a)\) это четвертая четверть, и котангенс там отрицателен.
«Точка привязки» - вертикальная, то есть функцию меняем. Окончательно имеем \(ctg(\frac+a)=-tg\,a\).
Важное замечание! На самом деле преобразовывать функцию по формулам приведения можно было сразу после получения \(ctg(-\frac-a)\), не делая все последующие преобразования.
Действительно:
\((-\frac-a)\) – это первая четверть, там котангенс положителен.
«Точка привязки» - вертикальная, то есть функцию меняем.
Таким образом, можно сразу получить, что \(ctg\,(-\frac-a)=tg\,a\).
«Точки привязки» не ограничиваются только лишь значениями \(\frac\),\(π\),\(\frac\) и \(2π\), а могут быть любой из точек, лежащих на пересечении круга с осями: \(5π\),\(-\frac\),\(-12π\),\(\frac\)…
Но обратите внимание – они никогда не могут быть \(-\frac\),\(\frac\),\(\frac\) и т.д. – потому что эти точки не лежат на пересечении с осями. Давайте, вместе выясним почему это так.
Формулы приведения. Примеры из ЕГЭ

Как вы, наверное, уже обратили внимание, формулы приведения разработаны для углов, представленных в одном из следующих видов: \(\frac<\pi>+a\), \(\frac<\pi>-a\), \(π+a\), \(π-a\), \(\frac<3\pi>+a\), \(\frac<3\pi>-a\), \(2π+a\) и \(2π-a\). Аналогично их можно использовать для углов представленных в градусах: \(90^°+a\), \(90^°-a\), \(180^°+a\), \(180^°-a\), \(270^°+a\), \(270^°-a\), \(180^°+a\), \(180^°-a\).
К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.
Менять ли функцию на кофункцию или оставить прежней?
Здесь правило еще проще:
- если «точка привязки» \(\frac<\pi>\) (\(90^°\)) или \(\frac<3\pi>\) (\(270^°\))– функция меняется на кофункцию;
- если «точка привязки» \(π\) (\(180^°\)) или \(2π\) (\(360^°\)) – функция остается той же.
То есть, при аргументах исходной функции \(\frac<\pi>+a\), \(\frac<\pi>-a\), \(\frac<3\pi>+a\) или \(\frac<\pi>-a\), мы должны поменять функцию, а при аргументах \(π+a\), \(π-a\), \(2π+a\) или \(2π-a\) - нет. Для того, чтоб это легче запомнить, вы можете воспользоваться мнемоническим правилом, которое в школе называют «лошадиным правилом»:
Точки, обозначающие \(\frac<\pi>\) \((90^°)\) и \(\frac<3\pi>\) \((270^°)\), расположены вертикально, и если вы переводите взгляд с одной на другую и назад, вы киваете головой, как бы говоря «да».

Точки же, обозначающие \(π\) (\(180^°\)) и \(2π\) (\(360^°\)), расположены горизонтально, и если вы переводите взгляд между ними, вы мотаете головой, как бы говоря «нет».

Эти «да» и «нет» - и есть ответ на вопрос: «меняется ли функция?».
Таким образом, согласно правилу, в нашем примере выше \(\cos(\frac-a)=. \) косинус будет меняться на синус. В конечном итоге получаем, \(\cos(\frac-a)=-\sin\) \(a\). Это и есть верная формула приведения.
Формулы приведения. Как запомнить?
Формулы приведения ! Они относятся к разделу «тригонометрия» в математике. Суть их заключается в приведении тригонометрических функций углов к более «простому» виду. О важности их знания написать можно много. Этих формул аж 32 штуки!
Не пугайтесь, учить их не надо, как и многие другие формулы в курсе математики. Лишней информацией голову забивать не нужно, необходимо запоминать «ключики» или законы, и вспомнить или вывести нужную формулу проблемой не будет. Кстати, когда я пишу в статьях «… нужно выучить. » – это значит, что действительно, это необходимо именно выучить.
Если вы с формулами приведения не знакомы, то простота их вывода вас приятно удивит – есть «закон», при помощи которого это легко сделать. И любую из 32 формул вы напишите за 5 секунд.
*А тем, кто хочет набить руку решая задачи, вот здесь разобраны 22 примера от простых до самых сложных.
Перечислю лишь некоторые задачи, типы которых возможны на экзамене, где без знания этих формул есть большая вероятность потерпеть фиаско в решении. Например:
– задачи на решение прямоугольного треугольника, где речь идёт о внешнем угле, да и задачах на внутренние углы некоторые из этих формул тоже необходимы.
– задачи на вычисление значений тригонометрических выражений; преобразования числовых тригонометрических выражений; преобразования буквенных тригонометрических выражений.
– задачи на касательную и геометрический смысл касательной, требуется формула приведения для тангенса, а также другие задачи.
– стереометрические задачи, по ходу решения не редко требуется определить синус или косинус угла, который лежит в пределах от 90 до 180 градусов.
И это лишь те моменты, которые касаются ЕГЭ. А в самом курсе алгебры есть множество задач, при решении которых, без знания формул приведения просто не обойтись.
Так что же к чему приводится и как оговоренные формулы упрощают для нас решение задач?
Например, вам нужно определить синус, косинус, тангенс или котангенс любого угла от 0 до 450 градусов:
угол альфа лежит пределах от 0 до 90 градусов
Итак, необходимо уяснить «закон», который здесь работает:
1. Определите знак функции в соответствующей четверти.
2. Запомните следующее:
функция изменяется на кофункцию
функция на кофункцию не изменяется
Что означает понятие — функция изменяется на кофункцию?
Ответ: синус меняется на косинус или наоборот, тангенс на котангенс или наоборот.
Теперь по представленному закону запишем несколько формул приведения самостоятельно:
Данный угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:
Угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Меняем функцию на кофункцию, так как у нас 270 градусов, значит:
Угол лежит в первой четверти, синус в первой четверти положителен. Не меняем функцию на кофункцию, так как у нас 360 градусов, значит:
Вот вам ещё дополнительное подтверждение того, что синусы смежных углов равны:
Угол лежит во второй четверти, синус во второй четверти положителен. Не меняем функцию на кофункцию, так как у нас 180 градусов, значит:
Проработайте мысленно или письменно каждую формулу, и вы убедитесь, что ничего сложного нет.
В статье на решение прямоугольного треугольника был отмечен такой факт – синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём.
И наоборот – косинус одного острого угла в прямоугольном треугольнике равен синусу другого острого угла в нём. Вот вам и подтверждение этого с помощью формул приведения:
Конечно, определить значения углов можно и без формул приведения, по тригонометрической окружности. И если вы умеете это делать, то очень хорошо. Но поняв, как работают формулы приведения, вы сможете делать это очень быстро.
Данные формулы можно также выразить в табличной форме:
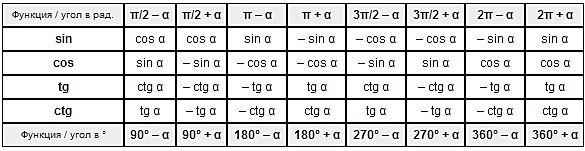
В дальнейшем, применяя свойство периодичности, четности (нечётности) вы без труда определите значение любого угла: 1050 0 , -750 0 , 2370 0 и любые другие. Статья об этом в будущем обязательно будет, не пропустите!
Когда в решениях задач буду использовать формулы приведения, то обязательно буду ссылаться на эту статью, чтобы вы всегда смогли освежить в памяти представленную выше теорию. На этом всё. Надеюсь, материал был вам полезен.
Как быстро получить любую формулу приведения
Для начала обратите внимание, что все формулы имеют похожий вид:

Здесь нужно пояснить термин «кофункция» - это та же самая функция с добавлением или убиранием приставки «ко-». То есть, для синуса кофункцией будет косинус, а для косинуса – синус. С тангенсом и котангенсом – аналогично.
Таким образом, например, синус при применении этих формул никогда не поменяется на тангенс или котангенс , он либо останется синусом, либо превратиться в косинус . А котангенс никогда не станет синусом или косинусом, он либо останется котангенсом, либо станет тангенсом. И так далее.
Едем дальше. Так как исходная функция и ее аргумент нам обычно даны, то весь вывод нужной формулы сводится к двум вопросам:
- как определить знак перед конечной функцией (плюс или минус)?
- как определить меняется ли функция на кофункцию или нет?
Плиз, хелп! Как выразить косинус через синус?
Вот, например, дано выражение cos пи\9, там по формулам приведения с пи\2? Объясните, пожалуйста, что дальше :сс

Чтобы уметь выражать косинус через синус с помощью формул приведения, сначала нужно разобраться с этими формулами. Их довольно много, вот парочка из них:
sin(90-a)=cosa
sin(180+a)=-sina
cos(270+a)=sina
cos(360+a)=cosa
Именно этими углами(90(π/2) , 180(π), 270(3π/2), 360(2π)) мы пользуемся в формулах приведения. И ещё одно, угол a∈(0;90).
Но чтобы их все не запоминать, нужно запомнить закон с помощью которого можно вывести любую из них. Итак нужно запомнить в каких четвертях cos, sin, tg, ctg положительны или отрицательны. Всё это есть во вложении. Легче запомнить если кое что уяснить sin положителен когда положительна ось ординат(её часто обозначают y), cos - когда положительная ось абсцисс(x), tg и ctg (это sin/cos(cos/sin)) поэтому они положительны когда одновременно положительны или отрицательны cos и sin. С этим вроде бы разобрались.
Теперь ещё один закон:
при углах 90 и 270 функция изменяется на кофункцию.
при углах 180 и 360 функция не изменяется.
Изменение на кофункцию - замена косинуса синусом(и наоборот) и замена тангенса котангенсом(и наоборот).
Теперь попробуем решить ваш пример:
cos(π/9) нам нужно заменить на sin. Вспомним что при углах π/2 и 3π/2 функция изменяется на кофункцию, поэтому представим π/9 в виде суммы(разности) с одним из этих углов:
π/2=9π/18
π/9=2π/18=9π/18 - 7π/18
cos(π/9)=cos(π/2 - 7π/18)=[π/2 - 7π/18 это 1 четверть, cos в ней положителен, знак при замене не меняется]=sin(7π/18).
Будут вопросы - спрашивайте.

Новые вопросы в Алгебра
ПОЖАЛУЙСТА ПОМООООГИТЕЕЕКоординаты неравенства x + (y + 1) 9 в координатной плоскости Решения - это изображения набора точек и количества (x; y) естес … твенных Определите, что пара чисел является ее решением.
СРОЧНО ПОЖАЛУЙСТА ПОМОГИТЕ очень нужно. Если можно, то с объяснением на листке. Заранее благодарю
10.1. Какие из следующих выражений являются одночленами: 8а; -0,5bc; 2/3x²yz; x-2/3; y+1/z; 10a/5; 4/b
Решите: 20×(5 1/3×3/4-2 1/7:5/7)3 1/3×1,5=Второе задание: вычислите значение выражения и сравниие их:3a-2(b+c) и a+3(b+c) при а=5 и b+c=3Задание трети … е:Упростите вырожения:(5x-1)-(2-8x)= при x=0,75 (6-2x)+(15-3x)=при x=0,2Задание четвёртое: раскройте скобки и цпростите вырожения:А) a-(a-(a-1)))Б)c+2(c-3×(c--1))Ставлю 5 звёзд
Как определить знак перед конечной функцией (плюс или минус)?
Какой знак был у исходной функции в исходной четверти, такой знак и нужно ставить перед конечной функцией.
Например, выводим формулу приведения для \(cos(\frac<3\pi>-a) =. \) С исходной функцией понятно – косинус, а исходная четверт ь ?
Для того, чтобы ответить на этот вопрос, представим, что \(a\) – угол от \(0\) до \(\frac<\pi>\), т.е. лежит в пределах \(0°…90^°\) (хотя это может быть не так, но для определения знака данная условность необходима). В какой четверти тригонометрической окружности при таком условии будет находиться точка, обозначающая угол \(\frac<3\pi>-a\)?
Чтобы ответить на вопрос, надо от точки, обозначающей \(\frac<3\pi>\), повернуть в отрицательную сторону на угол \(a\).

В какой четверти мы окажемся? В третьей. А какой же знак имеет косинус в третьей четверти? Минус. Поэтому перед итоговой функцией будет стоят минус: \(cos(\frac<3\pi>-a)=-. \)
Как доказать формулу приведения, или почему «точки привязки» обязательно должны быть точками пересечения с осями
Возьмем какую-либо формулу приведения – например, вот эту \(\sin(\frac+a)=\cosa\) – и попробуем получить из левой части правую.
Что у нас слева? Синус суммы аргументов.
У нас на этот случай есть формула: \(\sin(x+y)=\sinx \cosy+\siny \cosx\)
Применим ее: \(\sin(\frac+a)=\sin\frac\cosa+\sina \cos\frac\)
Мы знаем, что \(\sin\frac=1, а \cos\frac=0\). Таким образом имеем окончательную цепочку преобразований:
Попробуем еще. Возьмем вот эту формулу: \(\cos(π-a)=-\cosa\)
Преобразовываем с помощью формулы разности в косинусе:
\(\cos(π-a)=\cosπ \cosa+\sina \sinπ=-1·\cosa+\sina·0=-\cosa\)
Опять всё верно.
Ну и еще одну: \(\cos(\frac+a)=\sina\)
Преобразовываем с помощью формулы суммы в косинусе:
А теперь присмотритесь к преобразованиям. Замечаете что-нибудь общее?
Да, всё верно - во всех случаях у нас одна из функций превращается в \(1\) или \(-1\), а вторая в \(0\). И именно благодаря этому - итоговое выражение становится проще!
А теперь давайте попробуем взять в качестве «точки привязки» не точку пересечения с осями, а какую-нибудь другую, например, \(\frac\):
Мда… Что-то такое себе упрощение получилось…
«Точки привязки» должны быть точками пересечения с осями, потому что только в этом случае получаются более простые выражения. Так происходит потому, что в точках пересечения круга с осями всегда одна из функций (синус или косинус) равна нулю, а вторая плюс или минус единице. Для всех остальных точек – это не работает.
Читайте также:


