Кинематика своими руками
Кинематика — есть процесс вычисление позиции в пространстве для конца взаимосвязанной структуры при заданных углах поворота всех шарнирных точек (Joints). Это легко осуществляется, если есть только одно решение. Инверсная кинематика делает обратное. Для данной конечной точки вычисляются необходимые углы поворота шарниров таким образом, чтобы удалось достичь этой конечной точки. При этом могут возникнуть трудности, если есть много или бесконечно много решений.
Данный процесс чрезвычайно полезен в робототехнике. Например, вы захотели, чтобы рука робота потянулась и взяла объект. Если программа знает местоположение объекта относительно плечевого сустава, то ей достаточно расчитать углы поворота шарниров чтобы достичь объекта. Также инверсная кинематика полезна в 3D играх. Возьмем для примера дракона с очень длинной шеей. Дракон должен реалистично изогнуть шею и слопать игрока стоящего на полу. Или игрок захотел поднять с пола некий объект или нажать на кнопку. Пользователь увидит на экране как игрок потянется и коснется объекта, вместо того чтобы просто махнуть рукой где-то вблизи объекта (как например в Alone In The Dark).
Нет решений
Существует много случаев, когда связанная структура не в состоянии достичь цели. Например вы не можете коснуться локтем одной руки запястья той же руки. Или достать с земли до верхушки высокого дерева.
Одно решение
Два решения
В случае если есть два решения, то должна существовать техника выбора, какое из решений больше отвечает текущему состоянию структуры.
Много решений
Когда используется более двух шарниров, часто случается, что существует много решений задачи. Тем не менее, некоторые решения являются лучше других. Если ваша структура представляет, например, руку то некоторые решения более удобны, другие очень неестественны. Часто есть оптимальное решение.
Об алгоритме
Я пришел к методу инверсной кинематики после некоторых раздумий, проб и ошибок. Нет сомнений, что есть много алгоритмов решения проблем инверсной кинематики, но здесь я опишу только один.
Этот алгоритм не сразу находит решение. Это не простая функция где вы задаете место назначения и получаете углы. Это итеративный алгоритм, что делает алгоритм более реалистичным в программах, особенно в играх, где вы наверяка хотите, чтобы объекты двигались сглажено.
Решение находится за счет виртуального применения силы к концу цепочки и перетаскивания конца цепочки в конечную позицию. Сила действует на каждое сочленение и двигает структуру немного ближе к конечной точке. Так что даже если решения нет, цепочка приблизится к конечной точки так близко, насколько это возможно. Так как шарниры рассчитываются раздельно, то вы можете задать им разные свойства, такие как жесткость, эластичность и т.д. Каждый из шарниров также может иметь оптимальную позицию, которую алгоритм будет пытаться достичь так близко, как только это возможно.
Инверсная кинематика в 2D
Начнем с одного шарнира. В данном случае он может вращаться вокруг только одной оси (направление против часовой стрелки выберем как положительное). Вектор R действует под прямым углом к кости. Вектор силы F действует от конечной точки в направлении цели. Угол между R и F есть a. Теперь все совсем просто. Скорость, с которой вы должны поворачивать шарнир, пропорциональна скалярному произведению (dot product) векторов R и F. Придерживаясь точки зрения, что скалярное произведение двух векторов положительное число, и, конечно же, шарнир должен вращаться в положительном направлении, чтобы максимально приблизится к цели. Если угол между R и F прямой, то шарнир повернулся так, чтобы кость была максимально близко к цели и поэтому шарнир не должен больше поворачиваться. В этой точке скалярное произведение двух векторов даст ноль.
Ну вот, приехали. Случай потяжелее. Впредь, все будет просто разновидностью данного случая. Когда вы имеете больше одной кости вы просто должны повторить вышеописанный алгоритм для каждого шарнира по очереди.
Начнем с шарнира ближайшего к цели:
1. Вычислим вектор силы (от конечной точки к цели)
2. Вычислим скалярное произведение вектора силы и вектора, перпендикулярного кости.
3. Умножим скалярное произведение на небольшое число (например 0.01)
4. Добавим его к углу шарнира.
Делаем так для всех шарниров последовательно.
Инверсная кинематика в 3D
В трехмерном пространстве вычисления будут не намного сложнее. Есть три возможных оси, вокруг которых шарнир может вращаться. Я попытался применить вышеописанный метод в трехмерном пространстве, но результаты были не слишком хорошими. Я не до конца понял почему. Тем не менее эта математика безусловно работает. Есть нечто, что требует большого количества изменений установок, чтобы все работало, безусловно, правильно.
Ну, что ж, двигаемся дальше.
Ось шарнира перпендикулярна кости
Сперва давайте попробуем пример, приведенный выше, но в этот раз в 3D. Это система с двумя шарнирами и мы сперва возьмем первый шарнир.
Дадим названия векторам
a - Вектор вдоль оси шарнира.
b - Вектор вдоль кости.
r - Вектор перпендикулярный a и b.
f - Вектор силы (действующий от конечной точки к цели).
Если вектор силы будет параллелен a, шарнир не будет вращаться. Если он параллелен b, то вы просто тащите кость, шарнир не будет вращаться. Вооружившись данными пустулатами, я решил что вращающий момент должен быть пропорционален синусу угла между a и f и синусу угла между b и f.
Если конечная точка пришла в точку цели, то вы не хотите, чтобы структура двигалась, но если конечная точка далеко от цели, то вы хотите, чтобы структура двигалась быстро. Следовательно, вращающий момент должен быть пропорционален длине вектора силы.
Есть только одна вещь, которую нельзя понять из вышеописанного - направление в котором должен вращаться шарнир. Пусть шарнир должен вращатсья в положительном направлении если вектор силы направлен вдоль r, и в противоположном направлении в случае если вектор силы направлен противоположно r.
Сложив все воедино получим:
torque = Mag(f) * SinVect(a, f) * SinVect(b, f) * sign(CosVect(r, f)) * Sensitivity
В данной формуле SinVect и CosVect возвращают соответственно синус и косинус угла между векторами. Mag возвращает длину вектора, и sign возвращает знак числа. Sensitivity - это просто небольшая скалярная константа.
Теперь вы можете двигаться к следующему шарниру в структуре. Вычислим новые значения векторов a,b и f, и вычислим крутящий момент для шарнира 2. Вычислим крутящий момент для всех шарниров в структуре и добавим к углу каждого шарнира по его крутящему моменту. Конечная точка должна теперь быть ближе к цели. Непрерывно повторяя процесс мы сможем приблизить конечную точку структуры к цели максимально близко или даже коснутся цели.
Ось шарнира направлена вдоль кости
Хорошо, давайте взглянем на более трудный случай. Но здесь нет ничего нового. Здесь вы видите связанную структуру состоящую из четырех шарниров. Шарнир номер два, тем не менее, может вращаться вокруг оси своей кости. Это похоже на изгиб вашего запястья. И конечно этот шарнир наиболее важен. Как и в предыдущем случае, вектор a будет проходить вдоль оси шарнира, но в этом случае это еще и вдоль кости. Вектор b сейчас идет от шарнира к конечной точке. Вектор r как и раньше перпендикулярен обоим.
Чтобы достичь цели шарнир 2 должен повернуться на 90 градусов (см. правую картинку).
И закончим тем, что вектор b различен для шарниров чья ось вращения параллельна кости.
Дополнительные замечания.
Теперь, когда вы освоили базу инверсной кинематики, есть еще задача регулировки системы, чтобы задать ее поведение в различных ситуациях. Как я говорил до этого, есть много разных решений. Некоторые лучше, некоторые хуже. Различаются тем как они смотрятся, величиной затраченных движений или удобством.
Сглаживание кривых
Реальная змейка на реальной анимации редко когда запутывается сама в себе. Она имеет тенденцию образоввывать довольно гладкие кривые. Змейка в демке сделана из пар шарниров оси, которые перпендикулярны друг другу. Первоначально написанная змейка двигалась не слишком реалистично. Поэтому я добавил ей немного элластичности в шарнирах. Из-за этого шарниры сопротивляются изгибу. Чем больше вы их сгибаете, тем более они сопротивляются. Эффект от этого такой, что изгиб разпространяется по шарнирам.
Давайте взглянем на динозавра. Он очень толстый в теле, но становится более тонким и гибким в шее. Это свойство может быть симулировано связанной структурой, сочленения которой все более и более элластичны к концу.
Удобное положение
Конечности предпочитают находится в удобном положении. Это может быть выполнено новым добавлением элластичности шарнирам. Тем не менее в этом случае может быть наилучшим иметь определенный ряд положений для каждого шарнира в котором нету сопротивления. Этот ряд может быть рассмотен как удобный. После того как шарнир покидает удобное положение он будет сопротивлятся все сильнее и сильнее пока совсем не откажется вращаться.
Также может быть желательно держать конечность максимально низко. Люди редко долго держат свои руки на весу более, чем это необходимо. Поэтому положение выбирается исходя из минимальной энергии требующейся для удерживания положения.
Содержание
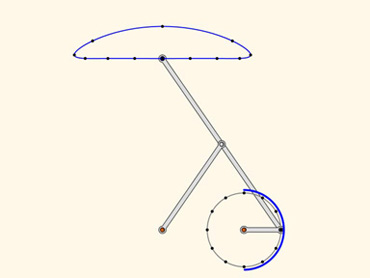

- Пафнутий Львович Чебышев, будучи профессором Санкт-Петербургского университета

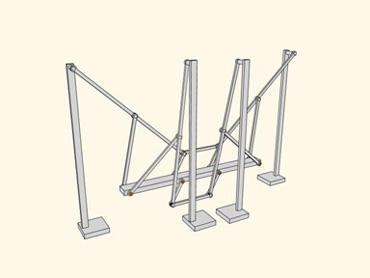
- Механизм Кланна имеет множество преимуществ шагающего механизма,
и лишён, в то же время, некоторых свойственных им ограничений. Он может перешагивать через бордюры, взбираться по ступеням, которые недоступны для колёсных движителей, и в то же время этот механизм не требует управления его двигателями со стороны микропроцессоров, причём количество этих двигателей может быть уменьшено по сравнению с другими видами техники, предназначенной для выполнения тех же функций.По своей классификации этот механизм находится между шагающими устройствами и колёсными машинами с управляемыми осями.


- Тео Янсен (Theo Jansen) (родился 17 марта, 1948, Гаага, Нидерланды) —
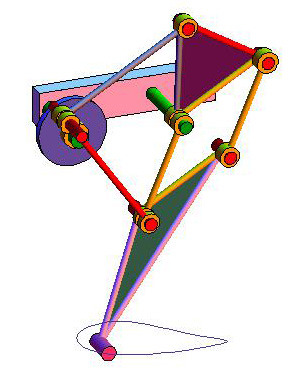
Глядя на механизм Тео Янсена так и хочется, чтобы можно было на нем прокатиться (или пройтись). Вот мне и пришла в голову идея создать такой аппарат, на котором можно было бы передвигаться. Для начала в уменьшенном масштабе. Но если мы хотим на нем передвигаться, то нам необходимо, чтобы данный аппарат мог поворачивать.
Можно сделать его из двух независимых частей и установить на них 2 двигателя и затем, управляя их скоростью, поворачивать т.е. так же, как поворачивают любые гусеничные машины.
Если вы едете по песку или любому сыпучему материалу, то может так случится, что колесо забуксует. Но с шагающими механизмами такой проблемы не возникает.
На данный момент разработан и отлажен процесс изготовления. И в результате функционирует одна из двух частей.
Данная платформа создается из оргстекла, алюминиевых трубок, винтов и гаек. В общем-то не такие уж и редкие материалы. Материалы избирались на основе дешевизны, простоты использования и эстетических соображений. Но началось все с эскиза всех основных деталей в масштабе 1:1 который приводится ниже:
Здесь можно изучать кинематику движения. Вы можете самостоятельно сконструировать ваш механизм, добавить новые узлы, стержни, отключать гравитацию, устанавливать перо, которое будет рисовать траекторию узла. Стержни можно растягивать и сжимать. Инструкцию смотрите внизу.
- Левая кнопка мышки: перемещение точки (узла, стержня, связи и т.п.)
- Нажмите ctrl для входа/выхода из редактирования режима.
- Клавиша "G" - включить/выключить гравитацию.
- Клавиша "R" - удалить трассировку.
В режиме редактирования:
- Клик левой кнопкой мышки - добавить точку.
- Клик правой кнопкой мышки - удалить точку.
- Выберите любые две точки, чтобы соединить их.
- Нажмите shift, чтобы отменить выделение.
- Нажмите "F" и выберите точку, чтобы зафиксировать/освободить ее.
- Нажмите "P" и выберите точку для установки/удаления пера для траектории.
- Новая точка свяжется с последней по умолчанию.

В робототехнике, есть две основные задачи кинематики:
прямая и обратная.
Рассмотрим эти задачи на стандартном примере манипулятора.
Прямая задача — это вычисление положения (X, Y, Z) рабочего органа манипулятора по его кинематической схеме и заданной ориентации (A1, A2… An) его звеньев (n — число степеней свободы манипулятора, A — углы поворота).
Обратная задача — это вычисление углов (A1, A2… An) по заданному положению (X, Y, Z) рабочего органа и опять же известной схеме его кинематики.
Очевидно, что более распространённой и важной является именно обратная задача кинематики.
Но нужно иметь в виду, что эта задача редко может быть решена однозначно.
Дело в том, что хотя для углов (A1, A2, . An) всегда существует ЕДИНСТВЕННОЕ положение (X, Y, Z) рабочего органа, но не факт, что для положения (X, Y, Z) отыщется такая же единственная комбинация углов (A1, A2, . An).
Скорее всего, достичь заданного положения (X, Y, Z) возможно и при другой комбинации углов (A1', A2', . An').
При решении обратной задачи аналитически, эта неоднозначность проявляется в явном виде (например, через квадратные корни).
Рассмотрим пример прямой задачи кинематики.

у нас есть манипулятор, способный работать только в одной плоскости и имеющий два сустава.
Первый сустав L1 закреплён на основании и повёрнут на угол Q1,
второй сустав L2, крепится к концу первого сустава и повёрнут относительно него на угол Q2.
Рабочий орган манипулятора находится на конце второго сустава.
Прямая задача кинематики состоит в нахождении координат рабочего органа (x, y) по заданным L1, L2, Q1, Q2.
L1 и L2 — это, соответственно, длины плеча и локтя манипулятора; определены конструкцией манипулятора.
Решение:
здесь, мы имеем две системы отсчёта — первая, связанная с точкой крепления плеча L1 — O, а вторая — с началом координат в точке крепления локтя — A.
Найдём смещение второй системы относительно первой (координаты точки A в системе отсчёта O):
Координаты (x, y) в системе отсчёта локтя:
По рисунку видно, что в системе O, локоть L2 повёрнут относительно плеча на Q1+Q2:
Теперь, рассмотрим пример обратной задачи кинематики.

тот же рисунок, но теперь нужно найти такие углы Q1 и Q2, которые позволят манипулятору с плечом L1 и локтем L2 поместить рабочий орган в заданную точку (x, y)
Проведём прямую B, соединяющую начало координат O с заданной точкой (x, y).
q1 — угол между осью OX и прямой B
q2 — угол между прямой B и плечом L1
, а q2 находим при помощи теоремы косинусов, которая говорит:
Для плоского треугольника со сторонами a,b,c и углом alpha, противолежащим стороне a, справедливо соотношение:
в нашем случае, по теореме косинусов:
по той же теореме косинусов найдём угол Q2:
как видно по рисунку, угол Q2 равен 180 — угол OAx

Очевидно, что руку можно расположить и по-другому:
формулы для Q1 и Q2 не изменятся, но изменятся знаки углов:

а Q2 нужно брать с противоположным знаком.
Откуда берётся изменение знака? Из вычисления квадратного корня, которое всегда даёт ответ со знаком плюс-минус.
Данный урок посвящен элементарному, но полезному построению: найдем ось вращения для простейшего механизма с одной степенью свободы. При разработке различных механизмов бывает известно требуемое положение подвижной детали, а чаще – два положения, исходное и рабочее, или открытое и закрытое и т.д. В этих случаях конструктору необходимо определить положение оси вращения, чтобы затем спроектировать подвижный узел. Мы не будем особо уделять внимание самому механизму – это может быть что угодно, от ковша экскаватора до тонарма или, например, подъемной кровати. Опишем лишь элементарное геометрическое построение с использованием Autocad как основного инструмента конструктора.
Итак, нам заданы два положения детали и известно, что деталь должна вращаться вокруг неподвижной оси.
1. Запускаем Autocad. Можно работать как в стандартном интерфейсе 3D Modeling, так и в интерфейсе для двухмерного моделирования. Интерфейсы выбираем из списка, открывающегося при нажатии кнопки Workspace Switching в строке состояния Autocad (правый нижний угол экрана). Включим интерфейс 2D Drafting & Annotation.

Единственное важное условие – прямоугольники должны быть одинаковыми (это одна и та же деталь), поэтому проще всего нарисовать один, а затем скопировать его и повернуть копию на любой угол (не обязательно 90°). Один угол детали можно отметить, например, фаской, чтобы понимать, какое положение деталь занимает при повороте.
3. Начнем построение. Оно основано на элементарных геометрических законах, полностью приводить которые мы не будем. Отметим только, что срединный перпендикуляр к хорде окружности всегда проходит через центр этой окружности. Поскольку деталь вращается, одна и та же точка детали (например, угол) описывает окружность, а если соединить два положения этой точки – получится хорда этой окружности. Центр вращения детали – это центр такой окружности. Поэтому командой Line просто строим хорды для двух разных точек детали (привязка Object Snap должна быть включена, и при наведении на угол детали должен загораться желтый квадрат привязки Endpoint):

4. Теперь строим срединные перпендикуляры. Способов очень много, покажем один – с помощью примитива Construction line (прямая). Но сначала делаем правый клик на иконке объектной привязки и проверяем, включены ли опции Midpoint, Perpendicular и Intersection (средняя точка, перпендикуляр и пересечение). Затем включаем, если она отключена, трассировку объектной привязки Object Snap Tracking. Когда привязки включены, выбираем команду Construction line на панели Draw.
В качестве первой точки выбираем середину хорды (загорается желтый треугольник).

Двигаем перекрестье курсора в место, где примерно должен проходить перпендикуляр из первой точки. При приближении курсора к искомому месту первая точка обозначится символом перпендикуляра. В этом положении кликаем мышью.

Точно так же строим второй срединный перпендикуляр. В результате получаем такую картину:

Если по какой-то причине вы не можете воспользоваться трассировкой, можно пойти другим путем: вторую точку Construction line указать прямо на хорде, с привязкой Nearest (песочные часы), а затем повернуть линию на 90° относительно середины хорды.
5. Видимо, нетрудно догадаться, что нужный нам центр вращения лежит на пересечении двух бесконечных срединных перпендикуляров. Отметим его окружностью (Circle), указав ее центр с привязкой к пересечению прямых, а радиус задав произвольно:

Удалим вспомогательные линии.

Можно легко проверить правильность построения, выбрав команду Rotate (панель Modify) и указав в качестве базовой точки центр окружности, обозначающей ось (привязка Center, желтый кружок). При движении курсора по кругу деталь будет двигаться так, как будто она вращается на неподвижной оси:



При повороте на угол, равный углу между крайними положениями детали (в нашем случае 90°) контуры деталей совпадут.
Инструменты и приемы, которые мы здесь рассмотрели, полезны и при более сложных построениях, связанных с различными механизмами. Важно понимать принципы начертательной геометрии и уметь использовать мощные возможности черчения Autocad.
Читайте также:



